第17章函数及其图像复习
图片预览







文档简介
(共31张PPT)
第十七章 函数及其图象复习课
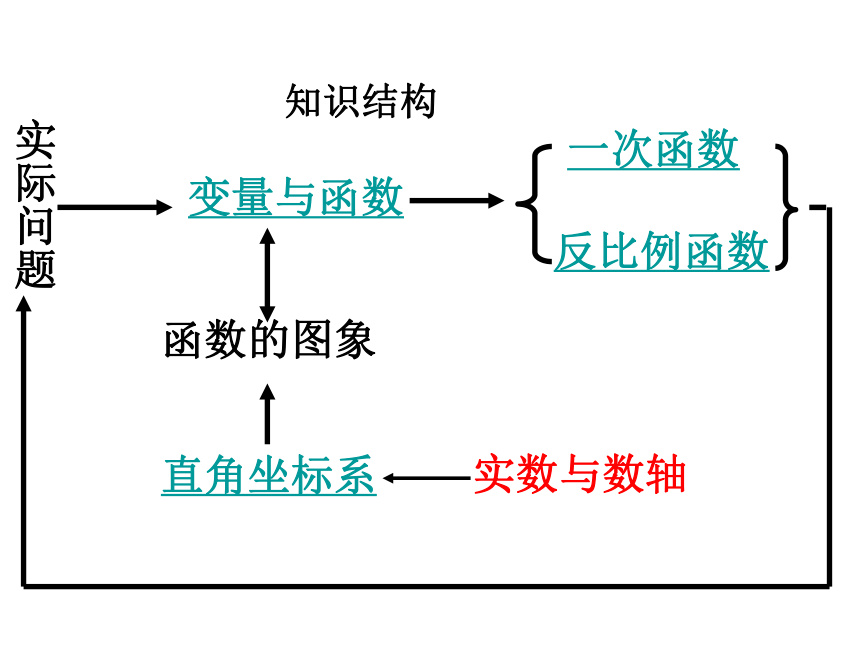
知识结构
变量与函数
一次函数
反比例函数
实践与探索
实际问题
变量与函数
一次函数
反比例函数
函数的图象
直角坐标系
实数与数轴
知识结构
在某一变化过程中,可以取不同数值的量,叫做变量 。
如果在一个变化过程中,有两个变量,例如x和y,对于x的每一个值,y都有惟一的值与之对应,我们就说x是自变量y是因变量此时也称y是x的函数 。
一、变量与函数
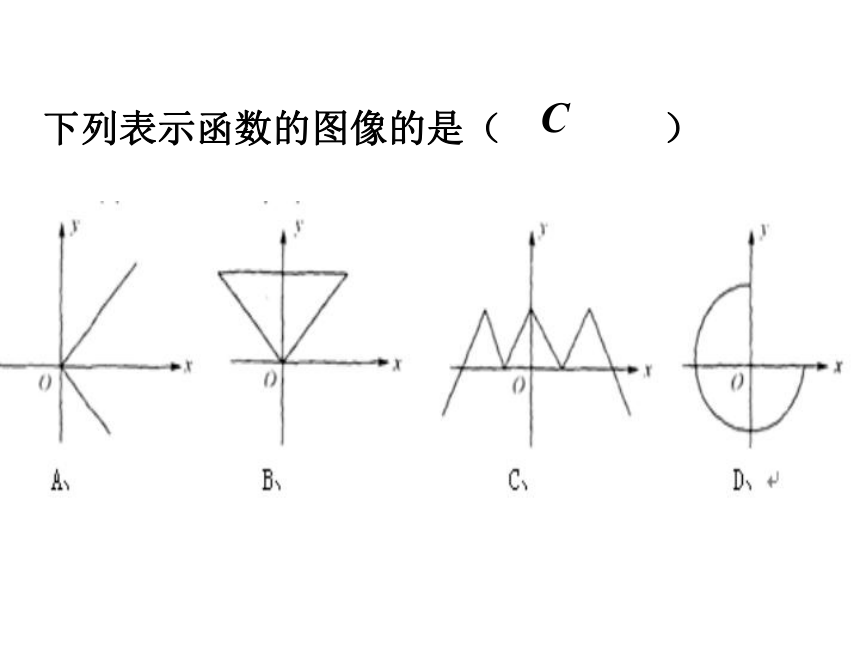
下列表示函数的图像的是( )
C
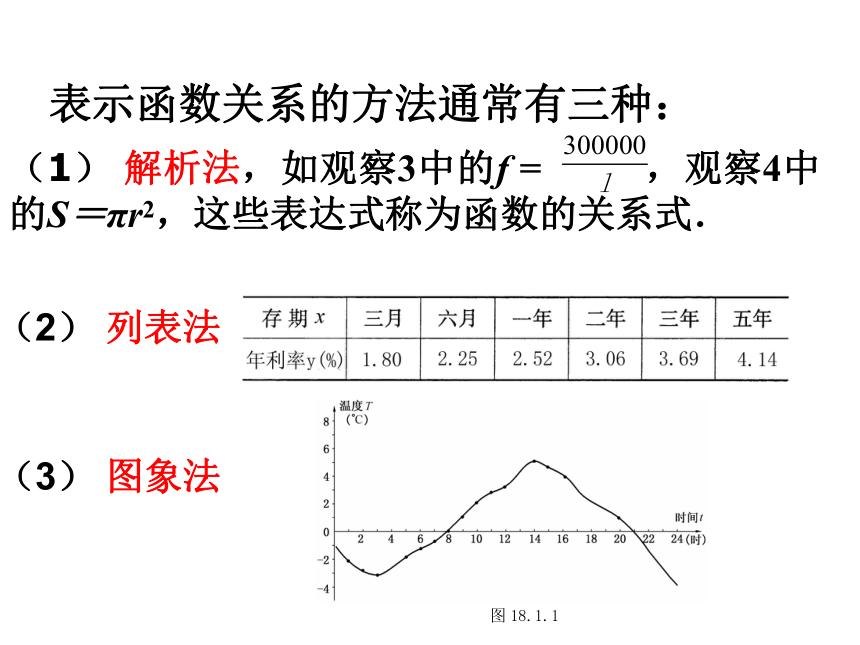
(1) 解析法,如观察3中的f = ,观察4中的S=πr2,这些表达式称为函数的关系式.
(2) 列表法
(3) 图象法
表示函数关系的方法通常有三种:
求自变量的取值范围应注意:
(1)分母≠0
(2)开偶次方时,被开方数≥0
求下列函数中自变量的取值范围:
⑴
⑶
⑵
⑷
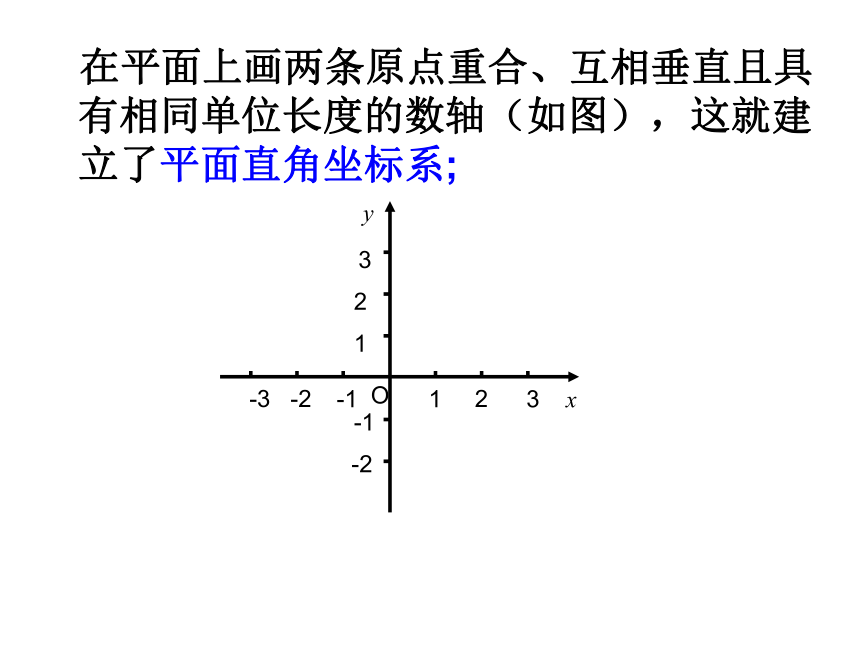
在平面上画两条原点重合、互相垂直且具有相同单位长度的数轴(如图),这就建立了平面直角坐标系;
O
1
2
3 x
-1
-2
-3
-1
-2
1
2
3
y
O
1
2
3 x
-1
-2
-3
-1
-2
1
2
3
y
P
(3,-1)
图中点P的坐标是多少?
请在图中标出Q(-3,2)的位置.
Q(-3,2)
在四个象限及坐标轴上的点的特征:
(+,+)
(-,+)
(-,-)
(+,-)
O
1
2
3 x
-1
-2
-3
-1
-2
1
2
3
y
(a,0)
(b,0)
2.点P(3-m,m)是第二象限内的点,则m的取值范围为( )
m>3
四
1.点(0,2)在( )
A. x轴上 B.y轴上 C.第三象限 D.第四象限
3.若点P(a,b)在第四象限,则点M(a-b,b-a)在第( )象限。
B
(1)关于x轴对称的两点:横坐标相同,纵坐标互为相反数;
即点p(a,b)关于x轴的对称点的坐标为(a,-b).
(2)关于y轴对称的两点:横坐标互为相反数,纵坐标相同;
即点p(a,b)关于y轴的对称点的坐标为(-a,b).
(3)关于原点对称的两点:横坐标坐标互为相反数,纵坐标也坐标互为相反数.
即点p(a,b)关于原点的对称点的坐标为(-a,-b).
关于x轴、y轴、坐标原点对称的两点的坐标特征:
点到两坐标轴的距离情况:
点P(a,b)到x轴的距离等于
到y轴的距离等于
A(-2,3)
A1(-2,-3)
A2(2,3)
A3(2,-3)
2.若点P(a,-2),Q(3,b)关于原点对称,则a-b=( )。
-5
1.若点A(-3,a)与点B(3,4)关于y轴对称,则a的值为( )。
4
3.若点P(a,-3)到y轴的距离是2,
则a=( )
±2
二、一次函数知识要点:
1、一次函数的概念:函数y=_______
(k、b为常数,k____)叫做一次函数。
当b___时,函数y=____(k____)叫做正比例函数。
kx +b
≠0
=0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。
1
k≠0
概括: (1)y=kx+b,当k>0时,y随x的增大而增大,这时函数的图象从左到右上升;
概括: (2)y=kx+b,当k<0时,y随x的增大而减小,这时函数的图象从左到右下降;
4、正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过 象限;
y随x的增大而 。
⑵当k<0时,图象过 象限;
y随x的增大而 。
一、三
增大
二、四
减小
5、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
增大
减小
k___0, k___0, k___0 , k —— 0,
b___0 , b___0 b___0 b___0
<
<
>
<
<
>
>
>
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号:
1.直线y=5x-10过点( ,0)、(0, )
2.直线y+2x=1与x轴的交点为 ,
与y轴的交点为 .
2
-10
(0.5,0)
(0,1)
3.已知函数 是正比例函数,则常数m的值 .
m=-3
4.已知一次函数y=kx-2,请你补充一个条件 ,使y随x的增大而减小。
k<0
练习
三、反比例函数
1一般地,形如
的函数叫做反比例函数.
2、反比例函数的变形形式:
1.当k>0时,图象的两个分支分别在第一、三象限内,在每个象限内,曲线至左向右下降,y随x的增大而减小;
2.当k<0时,图象的两个分支分别在第二、四象限内,在每个象限内,曲线至左向右上升, y随x的增大而增大。
y =
x
6
x
y
0
y
x
y
x
6
y =
0
反比例函数的性质
1、若双曲线 经过点A(m,-2m),则m 的值为 .
±2
3、当m为何值时,函数 是反比例函数,并求出其函数解析式.
2.如果双曲线 经过点(-2,3),那么
此双曲线也经过点( )
A.(-2,-3) B.(3,2)
C.(3,-2) D.(-3,-2)
C
练习
函数 正比例函数 反比例函数
解析式
图象形状
k>0
k<0
位置
增减性
位置
增减性
y=kx ( k≠0 )
( k是常数,k≠0 )
y =
x
k
直线
双曲线
一三象限
y随x的增大而增大
一三象限
y随x的增大而减小
二四象限
二四象限
y随x的增大而减小
y随x的增大而增大
填表分析正比例函数和反比例函数的区别
1.在同一坐标系中,正比例函数y=(m-1)x与反比例函数 的图象大致位置不可能是( )
x
y
0
x
y
0
x
y
0
x
y
0
(A)
(B)
(C)
(D)
A
3.如果反比例函数 (m为常数), 当 x>0时,y随x的增大而增大,那么m的取值范围是( ).
A. m>0 B. m<0 C. m<1 D. m>1
D
2、若反比例函数 的图象上有两点
A.正数 B.负数 C.非正数 D.非负数
A
4.已知一次函数的图象如下图,
(1)求出这个函数的关系式;
(2)求△ABO的面积
O
1
2
3 x
-1
-2
-3
-1
-2
1
2
3
y
A
B
四、实践与探索
引例
1.如图,直线y=kx+b与x轴交于A(-2,0),则方程kx+b=0的解是 ___________
x= -2
题后归纳:方程kx+b=0的解就是直线y=kx+b与x轴的交点横坐标。
1、明确:“两对应”:1)、方程对应着函数(不是解析式形式的方程可通过移项变为解析式形式);2)、方程组的解对应函数图像的交点坐标。2、画出每个方程对应的函数图像;3、找出这两个图像的交点,交点的横纵坐标分别对应方程组的x、y值
的解是————
如图,双曲线
与y=-2x+1的交点坐标 为(-1,3),(1.5,-2),则不等式
的解集为 _________
引例
总结:图像法解不等式,解集就是交点横坐标x1、x2与0的组合区间。
小结
1、知识上
2、研究问题的方法
从特殊到一般
_____________________________________________________________________________________
自己总结总结
第十七章 函数及其图象复习课
知识结构
变量与函数
一次函数
反比例函数
实践与探索
实际问题
变量与函数
一次函数
反比例函数
函数的图象
直角坐标系
实数与数轴
知识结构
在某一变化过程中,可以取不同数值的量,叫做变量 。
如果在一个变化过程中,有两个变量,例如x和y,对于x的每一个值,y都有惟一的值与之对应,我们就说x是自变量y是因变量此时也称y是x的函数 。
一、变量与函数
下列表示函数的图像的是( )
C
(1) 解析法,如观察3中的f = ,观察4中的S=πr2,这些表达式称为函数的关系式.
(2) 列表法
(3) 图象法
表示函数关系的方法通常有三种:
求自变量的取值范围应注意:
(1)分母≠0
(2)开偶次方时,被开方数≥0
求下列函数中自变量的取值范围:
⑴
⑶
⑵
⑷
在平面上画两条原点重合、互相垂直且具有相同单位长度的数轴(如图),这就建立了平面直角坐标系;
O
1
2
3 x
-1
-2
-3
-1
-2
1
2
3
y
O
1
2
3 x
-1
-2
-3
-1
-2
1
2
3
y
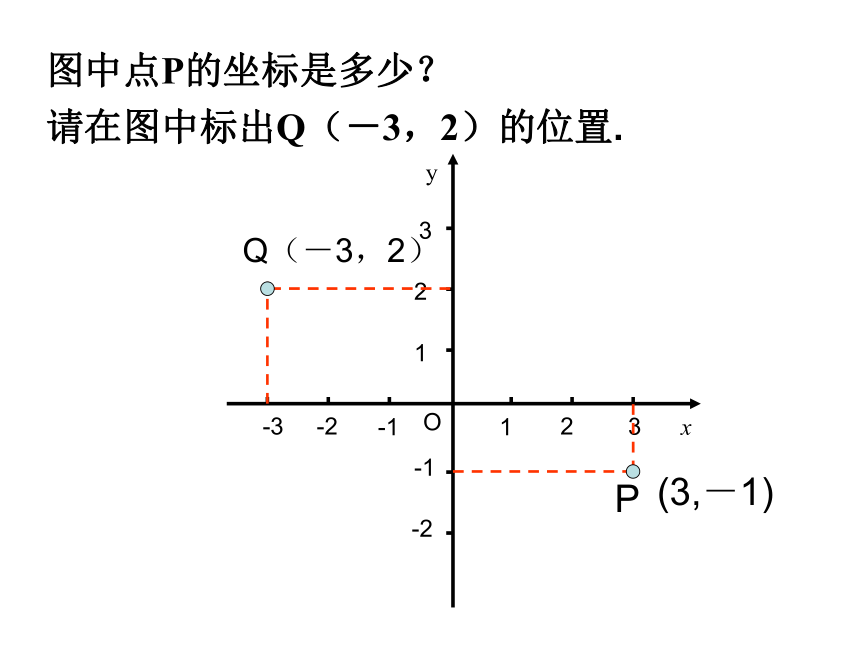
P
(3,-1)
图中点P的坐标是多少?
请在图中标出Q(-3,2)的位置.
Q(-3,2)
在四个象限及坐标轴上的点的特征:
(+,+)
(-,+)
(-,-)
(+,-)
O
1
2
3 x
-1
-2
-3
-1
-2
1
2
3
y
(a,0)
(b,0)
2.点P(3-m,m)是第二象限内的点,则m的取值范围为( )
m>3
四
1.点(0,2)在( )
A. x轴上 B.y轴上 C.第三象限 D.第四象限
3.若点P(a,b)在第四象限,则点M(a-b,b-a)在第( )象限。
B
(1)关于x轴对称的两点:横坐标相同,纵坐标互为相反数;
即点p(a,b)关于x轴的对称点的坐标为(a,-b).
(2)关于y轴对称的两点:横坐标互为相反数,纵坐标相同;
即点p(a,b)关于y轴的对称点的坐标为(-a,b).
(3)关于原点对称的两点:横坐标坐标互为相反数,纵坐标也坐标互为相反数.
即点p(a,b)关于原点的对称点的坐标为(-a,-b).
关于x轴、y轴、坐标原点对称的两点的坐标特征:
点到两坐标轴的距离情况:
点P(a,b)到x轴的距离等于
到y轴的距离等于
A(-2,3)
A1(-2,-3)
A2(2,3)
A3(2,-3)
2.若点P(a,-2),Q(3,b)关于原点对称,则a-b=( )。
-5
1.若点A(-3,a)与点B(3,4)关于y轴对称,则a的值为( )。
4
3.若点P(a,-3)到y轴的距离是2,
则a=( )
±2
二、一次函数知识要点:
1、一次函数的概念:函数y=_______
(k、b为常数,k____)叫做一次函数。
当b___时,函数y=____(k____)叫做正比例函数。
kx +b
≠0
=0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。
1
k≠0
概括: (1)y=kx+b,当k>0时,y随x的增大而增大,这时函数的图象从左到右上升;
概括: (2)y=kx+b,当k<0时,y随x的增大而减小,这时函数的图象从左到右下降;
4、正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过 象限;
y随x的增大而 。
⑵当k<0时,图象过 象限;
y随x的增大而 。
一、三
增大
二、四
减小
5、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
增大
减小
k___0, k___0, k___0 , k —— 0,
b___0 , b___0 b___0 b___0
<
<
>
<
<
>
>
>
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号:
1.直线y=5x-10过点( ,0)、(0, )
2.直线y+2x=1与x轴的交点为 ,
与y轴的交点为 .
2
-10
(0.5,0)
(0,1)
3.已知函数 是正比例函数,则常数m的值 .
m=-3
4.已知一次函数y=kx-2,请你补充一个条件 ,使y随x的增大而减小。
k<0
练习
三、反比例函数
1一般地,形如
的函数叫做反比例函数.
2、反比例函数的变形形式:
1.当k>0时,图象的两个分支分别在第一、三象限内,在每个象限内,曲线至左向右下降,y随x的增大而减小;
2.当k<0时,图象的两个分支分别在第二、四象限内,在每个象限内,曲线至左向右上升, y随x的增大而增大。
y =
x
6
x
y
0
y
x
y
x
6
y =
0
反比例函数的性质
1、若双曲线 经过点A(m,-2m),则m 的值为 .
±2
3、当m为何值时,函数 是反比例函数,并求出其函数解析式.
2.如果双曲线 经过点(-2,3),那么
此双曲线也经过点( )
A.(-2,-3) B.(3,2)
C.(3,-2) D.(-3,-2)
C
练习
函数 正比例函数 反比例函数
解析式
图象形状
k>0
k<0
位置
增减性
位置
增减性
y=kx ( k≠0 )
( k是常数,k≠0 )
y =
x
k
直线
双曲线
一三象限
y随x的增大而增大
一三象限
y随x的增大而减小
二四象限
二四象限
y随x的增大而减小
y随x的增大而增大
填表分析正比例函数和反比例函数的区别
1.在同一坐标系中,正比例函数y=(m-1)x与反比例函数 的图象大致位置不可能是( )
x
y
0
x
y
0
x
y
0
x
y
0
(A)
(B)
(C)
(D)
A
3.如果反比例函数 (m为常数), 当 x>0时,y随x的增大而增大,那么m的取值范围是( ).
A. m>0 B. m<0 C. m<1 D. m>1
D
2、若反比例函数 的图象上有两点
A.正数 B.负数 C.非正数 D.非负数
A
4.已知一次函数的图象如下图,
(1)求出这个函数的关系式;
(2)求△ABO的面积
O
1
2
3 x
-1
-2
-3
-1
-2
1
2
3
y
A
B
四、实践与探索
引例
1.如图,直线y=kx+b与x轴交于A(-2,0),则方程kx+b=0的解是 ___________
x= -2
题后归纳:方程kx+b=0的解就是直线y=kx+b与x轴的交点横坐标。
1、明确:“两对应”:1)、方程对应着函数(不是解析式形式的方程可通过移项变为解析式形式);2)、方程组的解对应函数图像的交点坐标。2、画出每个方程对应的函数图像;3、找出这两个图像的交点,交点的横纵坐标分别对应方程组的x、y值
的解是————
如图,双曲线
与y=-2x+1的交点坐标 为(-1,3),(1.5,-2),则不等式
的解集为 _________
引例
总结:图像法解不等式,解集就是交点横坐标x1、x2与0的组合区间。
小结
1、知识上
2、研究问题的方法
从特殊到一般
_____________________________________________________________________________________
自己总结总结
