分数四则混合运算解决问题强化训练难题篇(含答案)数学六年级上册苏教版
文档属性
| 名称 | 分数四则混合运算解决问题强化训练难题篇(含答案)数学六年级上册苏教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-07 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
分数四则混合运算解决问题强化训练(难题篇)数学六年级上册苏教版
1.修一条长60米的高速公路,已经修了40天,正好修了这条公路的,照这样计算,修完这条高速公路还要多少天?
2.客车的速度是小轿车速度的。现在两车同时从两地相向而行,在离中点15千米处相遇,相遇时小轿车行驶了多少千米?
3.某班同学开班会,一位男生上台主持时,台下男女生人数的比是3∶2,他下台后,一名女生上台主持时,台下男女生人数的比是5∶3,你知道这班有几人吗?
4.甲、乙从A、B两地同时相对开出,5小时后相遇。相遇后两车继续按原速行驶,又经过3小时甲车到达B地,乙车距A地还有120千米。A、B两地相距多少千米?
5.一个长方形的周长是50厘米,它长的与宽的一样长,这个长方形的面积是多少?
6.修一条路,第一周修多60米,第二周修余下的少40米,还剩320米。求全长多少米?
7.六年级某班有学生55人,选出女同学的参加踢毽子比赛后,剩下的男女生人数恰好相等,求这个班有女同学多少人?
8.一袋大米,用去后,又运来24千克,这时比原来少。求这时多少千克?
9.小明读一本故事书,已读的页数比没读的多,没读的页数比已读的少48页,小明已经读了多少页?
10.阳光小学组织五、六年级同学清理街头小广告。活动统计结果显示:六年级同学清理小广告420则,五年级比六年级少清理。五、六年级同学共清理小广告多少则?
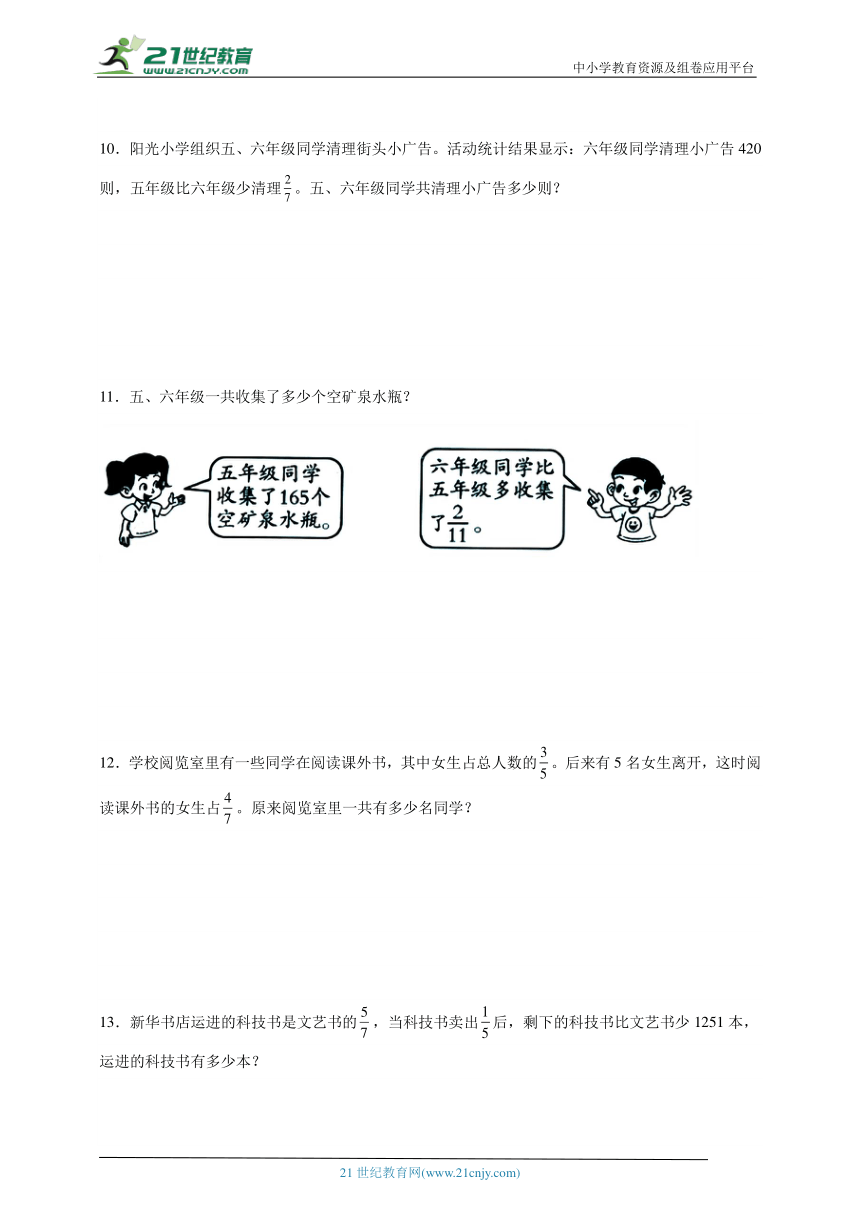
11.五、六年级一共收集了多少个空矿泉水瓶?
12.学校阅览室里有一些同学在阅读课外书,其中女生占总人数的。后来有5名女生离开,这时阅读课外书的女生占。原来阅览室里一共有多少名同学?
13.新华书店运进的科技书是文艺书的,当科技书卖出后,剩下的科技书比文艺书少1251本,运进的科技书有多少本?
14.菜场运来白菜吨,运来的黄瓜是白菜的,运来的黄瓜比萝卜少,运来的萝卜多少吨?
15.苏州体育中心停车场有大、小汽车共145辆,其中大汽车比小汽车多5辆。大、小汽车各有多少辆?
(1)画出线段图。
(2)列式解答。
16.一批零件,甲单独做20小时可以完成,乙单独做30小时可以完成。现在两人合作,完成任务时,甲比乙多做24个。这批零件共有多少个?
17.有甲、乙两个志愿者服务队,甲队有42人,把甲队的调入乙队,这时两队人数一样多。原来甲乙两队共有多少人?
18.小华和小明共有若干本故事书,已知小明的占总数的,若小华给小明10本,则两人的故事书同样多,小华和小明各有多少本故事书?
19.一堆煤36千克,第一天烧了它的,第二天烧了千克,两天共烧了多少千克?
20.某工厂有20吨的煤,第一天用去了,第二天用了剩下的,第二天用去多少吨煤?还剩多少吨煤?
21.六年级同学举行“小发明”比赛,六(1)班上交了40件作品,比六(2)班多交了,六(1)班和六(2)班共交了多少件作品?
22.某班原来男生人数和女生人数是3∶4,后来又转来2名男生,这时男生和全班人数的比是5∶11,现在男、女生人数各是多少?
23.两筐香蕉共重160千克,从第一筐里取出放入第二筐,两筐就一样重。原来两筐香蕉各重多少千克?(先画线段图,再解答)
24.加工一批零件,甲单独做小时完成,乙单独做小时完成,两人合做几小时完成任务的一半?
参考答案:
1.20天
【分析】根据题意,把全部修完需要的天数看成单位“1”,则40天占总天数的,根据分数除法的意义,即可求出总天数,减去已经修的天数即可。
【详解】40÷-40
=60-40
=20(天)
答:修完这条高速公路还要20天。
【点睛】此题考查了分数除法的应用,找准单位“1”,明确已知一个数的几分之几是多少,求这个数用除法。
2.70千米
【分析】根据题意,两车行驶的时间相同,客车的速度是小轿车速度的,所以客车行驶的路程也是小轿车的,把小轿车行驶的路程看作单位“1”,则客车行驶的是,在离中点15千米处相遇,则小轿车比客车多行驶15×2=30千米,对应的分率为(1-),根据分数除法的意义,解答即可。
【详解】15×2÷(1-)
=30÷
=70(千米)
答:相遇时小轿车行驶了70千米。
【点睛】此题考查了相遇问题,分别表示出两车行驶的路程,找出路程差是解题关键。
3.41人
【分析】一位男生上台主持或一位女生上台主持,台下的总人数相等。根据题意,男生上台主持时,台下的男生人数占总人数的;女生上台主持时,台下的男生人数占总人数的,这时的男生人数比刚才多1人。设台下的总人数为x人,根据女生上台时台下男生人数-男生上台时台下男生人数=1,列方程求出台下的总人数,最后加上台上的1人即是这班总人数。
【详解】解 :设台下的总人数为x人。
x-x=1
x-x=1
x=1
x=40
40+1=41(人)
答:这班有41人。
【点睛】本题主要考查比的应用。要理解台下的总人数相等,根据男生上台和女生上台时台下男生的人数变化列方程解答比较简便。
4.300千米
【分析】把A、B两地的距离看作单位“1”,根据题意可知,甲车、乙车每小时总共行全程的,甲车行完全程需要5+3=8小时,甲每小时行全程的,那么乙车每小时行全程的-,再乘8小时求出乙车行全程的分率,再用1减去它,求出剩下全程的分率,它对应的数是120,用除法求出A、B两地相距多少千米。
【详解】5+3=8小时
1-(-)×8
=1-
=
120÷=300(千米)
答:A、B两地相距300千米。
【点睛】解答此题的关键是找清题中的数量间的关系,考查了学生分析解决问题的能力。
5.150平方厘米
【分析】假设长为未知数x厘米,则宽为(50÷2-x)厘米,长的与宽的一样长,据此列出等式解方程求出长和宽,再根据长方形的面积公式求出面积。
【详解】解:设长为x厘米。
x=×(50÷2-x)
x=-x
x+x=
x=
x=15
50÷2-15
=25-15
=10(厘米)
15×10=150(平方厘米)
答:这个长方形的面积是150平方厘米。
【点睛】要熟练掌握长方形的周长和面积公式,用方程解答先找出等量关系,求出长和宽,进而求面积。
6.600米
【分析】由第二周修余下的少40米,还剩320米可知320-40所对应的是修第一周后剩下的,根据已知总量的几分之几是多少,求总量用部分的量除以对应的分率,求出修第一周后的长度,(320-40)÷=420米;第一周修多60米, 420+60对应的就是全长的1-,( 420+60)÷(1-)就是全长。
【详解】[(320-40)÷(1-)+60] ÷(1-)
=[280÷+60] ÷
=[420+60] ÷
=480×
=600(米)
答:全长600米。
【点睛】认真分析题意,找准题中分数的单位“1”,部分的量÷对应的分率=单位“1”的量。
7.30人
【分析】假设这个班女同学有x人,则男同学人数就是(55-x)人,选出女同学的参加踢毽子比赛后,剩下的女同学就是(1-)x,正好和男同学人数相等,据此列出方程解答。
【详解】解:设这个班女同学有x人。
(1-)x=55-x
x=55-x
x+x=55
x=55
x=30
答:这个班有女同学30人。
【点睛】用方程解答此题,关键是找出女同学的和男同学人数相等这个等量关系。
8.280千克
【分析】假设这袋大米有x千克,用去后剩下x,加上24千克后正好是原来的(1-)x,据此列方程解答求出一袋大米的质量,这袋大米的(1-)就是要求的问题。
【详解】解:设这袋大米有x千克。
(1-)x+24=(1-)x
x+24=x
x-x=24
x=24
x=320
320×(1-)
=320×
=280(千克)
答:这时280千克。
【点睛】用方程解答问题要先找出题中的等量关系,有时候不一定直接设要求的问题为未知数。
9.176页
【分析】把没读的页数看作单位“1”,已读的比没读的多,正好多48页,48÷求出没读的页数;已读的页数比没读的多,即已读的是没读的1+,即48的1+,用乘法求出即可。
【详解】48÷=48×=128(页)
128×(1+)
=128×
=176(页)
答:小明已经读了176页。
【点睛】找准单位“1”的量,看另一个量比单位“1”多几分之几,多多少页,用对应的量除以对应的分率求出单位“1”的量,是解题的关键。
10.720则
【分析】根据题意可知,把六年级清理的小广告数量看作“单位1”,则五年级清理小广告的数量为420×=300则,故五、六年级共清理小广告300+420=720则。
【详解】420+420×
=420+420×
=420+300
=720(则)
答:五六年级同学共清理小广告720则。
【点睛】本题主要考查了分数混合运算的应用。解答此类问题要弄清谁是“单位1”以及分率与量的对应关系。
11.360个
【分析】根据题意,把五年级收集的数量看作单位1,则六年级收集的个数是五年级的(1+)。先用五年级收集的个数乘(1+),求出六年级收集的个数,最后再加上五年级的个数即可。
【详解】165+165×(1+)
=165+165×
=165+195
=360(个)
答:五、六年级一共收集了360个空矿泉水瓶。
【点睛】本题考查分数四则混合运算的应用。明确六年级的个数占五年级的分率,从而求出六年级收集的个数是解题的关键。
12.75名
【分析】原来女同学占,则女生是男生人数的,同理可知,阅览室走出5名女生同学后,女生占男生人数的,所以这5名女生占男生人数的-,由此根据分数除法的意义求出男生人数后,即能求出总人数。
【详解】5÷(-)÷(1-)
=5÷(-)÷
=5÷÷
=75(名)
答:原来阅览室里一共有75名同学在看书。
【点睛】明确这一过程中男生人数没有变化,根据女生人数占男生人数分率的变化求出男生有多少人是完成本题的关键。
13.2085本
【分析】将文艺书的本数看成是单位“1”,那么剩下的科技书占文艺的几分之几=新华书店运进的科技书是文艺书的几分之几×(1-卖出几分之几),剩下的科技书比文艺书少几分之几=1-剩下的科技书的本数占文艺书的几分之几,所以运进文艺书的本数=剩下的科技书比文艺书少的本数÷剩下的科技书比文艺书少几分之几,所以运进科技书的本数=运进文艺书的本数×新华书店运进的科技书是文艺书的几分之几,据此代入数据作答即可。
【详解】1-×(1-)
=1-
=
1251÷=2919(本)
2919×=2085(本)
答:运来科技书有2085本。
【点睛】找准单位“1”以及具体数量1251本所对应的分率是解题关键,明确已知一个数的几分之几是多少,求这个数用除法,先求出文艺书的本数是解题关键。
14.吨
【分析】运来萝卜的吨数=运来黄瓜的吨数÷(1-运来的黄瓜比萝卜少几分之几),其中运来黄瓜的吨数=运来白菜的吨数×运来的黄瓜是白菜的几分之几,据此代入数据作答即可。
【详解】×÷(1-)
=
=(吨)
答:运来的萝卜吨。
【点睛】注意两次单位“1”是不同的,求一个数的几分之几用乘法,已知一个数的几分之几求这个数用除法。
15.(1)见详解
(2)45辆;100辆
【分析】先画一条线段表示小汽车的辆数,把它平均分成5份,再画一条线段表示大汽车的辆数,它比小汽车的2份多5辆。以小汽车辆数为单位“1”,把大汽车辆数减去5辆,大汽车辆数就刚好是小汽车的,此时总辆数是(145-5)辆,小汽车辆数占总数的(1+),根据分数除法的意义求出小汽车的辆数,进而求出大汽车的辆数即可。
【详解】(1)
(2)(145-5)÷(1+)
=140÷
=100(辆)
145-100=45(辆)
答:大汽车有45辆,小汽车有100辆。
【点睛】认真分析题意,找出题中单位“1”的量,再看比较量是单位“1”的量的几分之几或几倍,利用和倍问题求出单位“1”的量,注意总和里减去5才是(1+)所对应的量。
16.120个
【分析】把工作总量看作单位“1”,用工作总量÷工作时间=工作效率,分别求出甲、乙的工作效率;再用工作总量÷合作的工作效率之和=合作需要的时间求出合作的时间;完成任务时,甲比乙多做的零件个数24个÷合作的时间=每小时甲比乙多做的零件个数,最后用每小时甲比乙多做的零件个数÷(甲的工效-乙的工效)=这批零件的总个数,据此列式解答。
【详解】1÷(+)
=1÷
=12(小时)
24÷12=2(个)
2÷(-)
=2÷
=120(个)
答:这批零件共有120个。
【点睛】用工作总量除以工作效率之和求出合作时间,然后求出甲比乙每小时多做多少个零件,再用多做的数量除以对应的分率(两人工效之差)求出工作总量是解题的关键。
17.72人
【分析】先用乘法求出甲队的是多少人,即甲队调入乙队的人数,然后用甲队减去调入乙队的人数求出甲队现在的人数(也是乙队现在的人数),两队调动前后人数之和不变,则用甲队现在的人数乘2即可求出原来两队人数之和。
【详解】42×=6(人)
(42-6)×2
=36×2
=72(人)
答:原来甲乙两队共有72人。
【点睛】两队调动前后的人数之和不变,求出现在两队人数之和即是原来的人数之和。先求出甲队的现有人数是解题的关键。
18.80本;60本
【分析】“若小华给小明10本,则两人的故事书同样多”,说明小华原来的故事书比小明多2×10=20(本),小明的占总数的,则小华占总数的1-,比小明多总数的1--,根据分数除法的意义先求出总的本数,再分别求出各自的图书数即可。
【详解】10×2÷(1--)
=20÷
=140(本)
140×=60(本)
140-60=80(本)
答:小明有60本故事书,小华有80本故事书。
【点睛】本题考查了分数的乘法和分数除法的意义,注意解决此类问题中的量率对应关系。比如本题中多的20本对应多的分率1--。
19.3千克
【分析】把这堆煤看作单位“1”,第一天烧了它的,用乘法求出第一天烧的千克数,再加上第二天烧的千克数,即为两天共烧了多少千克。
【详解】36×+
=3+
=3(千克)
答:两天共烧了3千克。
【点睛】此题重在区分分数在具体的题目中的区别:在具体的题目中,带单位是一个具体的数,不带单位是把某一个数量看单位“1”,是它的几分之几。
20.4吨;12吨
【分析】把煤的总量看作单位1,则第一天用去20吨的,用乘法计算求出用去的吨数,继而求出剩下的吨数。第二天用去的是剩下的,继续用乘法求出第二天用去的吨数。用总量减去两天的用量即是剩下的吨数。
【详解】(20-20×)×
=(20-4)×
=16×
=4(吨)
20-20×-4
=20-4-4
=12(吨)
答:第二天用去4吨煤,还剩12吨煤。
【点睛】本题考查分数四则混合运算的实际应用。求一个数的几分之几是多少,用乘法计算。
21.75件
【分析】根据题意,六(1)班比六(2)班多交了,把六(2)班的作品数量看作单位1,则六(1)班的作品数量是六(2)班的(1+),已知六(1)班上交了40件作品,用除法求出单位1即六(2)班的数量。再把两班的数量合起来。
【详解】40÷(1+)+40
=40÷+40
=35+40
=75(件)
答:六(1)班和六(2)班共交了75件作品。
【点睛】本题考查分数四则混合运算的实际应用。已知单位1的几分之几是多少,求单位1,用除法。
22.男生有20人,女生有24人
【分析】把女生人数看作单位“1”,某班原来男生人数和女生人数是3∶4,即原来男生人数占女生人数的,现在男生和全班人数的比是5∶11,这说明女生人数有11-5=6(份),则现在男生人数占女生人数的,所以现在比原来多了女生的-,用2÷(-)即可求出女生人数,进而可以求出现在的男生人数。
【详解】11-5=6(份)
2÷(-)
=2÷(-)
=2÷
=24(人)
24×=20(人)
答:现在男、女生人数各是20人和24人。
【点睛】找准单位“1”和男生人数占女生人数的分率的变化是解题的关键,已知一个数的几分之几是多少,求这个数时用除法计算,求一个数的几分之几是多少时,用乘法计算。
23.第一筐112千克,第二筐48千克。
【分析】首先根据题意,按照线段图的画法及题目中的叙述画出线段图。我们可以把第一筐苹果的重量看作单位“1”,用“1”减去比第二筐多的分率的2倍,可以确定第二筐占第一筐的分率;再结合上述提示,不难得到两筐的重量和占第一筐的分率,然后结合已知,根据分数除法的意义,求出第一筐的重量,接下来用两筐的重量和减去第一筐的重量,即可求出第二筐的重量,从而完成解答。
【详解】线段图如下:
1-×2
=1-
=;
160÷(1+)
=160÷
=160×
=112(千克)
160-112=48(千克)
答:原来第一筐香蕉112千克,第二筐香蕉48千克。
【点睛】从“从第一筐里取出放入第二筐,两筐就一样重”这个关键的条件入手找出之间的等量关系,熟练掌握分数除法的意义,问题就可以迎刃而解。
24.小时
【分析】把这批零件看作单位“1”这批零件的一半就是,则甲的速度=1÷甲单独做完用的时间,乙的速度=1÷乙单独做完用的时间,求两人合做几小时完成任务的一半,直接用除以甲、乙的速度和即可。
【详解】÷(1÷+1÷)
=÷(2+3)
=÷5
=(小时)
答:两人合做完成任务的一半。
【点睛】找准单位“1”是解题的关键,掌握速度、时间和工作总量的关系。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
分数四则混合运算解决问题强化训练(难题篇)数学六年级上册苏教版
1.修一条长60米的高速公路,已经修了40天,正好修了这条公路的,照这样计算,修完这条高速公路还要多少天?
2.客车的速度是小轿车速度的。现在两车同时从两地相向而行,在离中点15千米处相遇,相遇时小轿车行驶了多少千米?
3.某班同学开班会,一位男生上台主持时,台下男女生人数的比是3∶2,他下台后,一名女生上台主持时,台下男女生人数的比是5∶3,你知道这班有几人吗?
4.甲、乙从A、B两地同时相对开出,5小时后相遇。相遇后两车继续按原速行驶,又经过3小时甲车到达B地,乙车距A地还有120千米。A、B两地相距多少千米?
5.一个长方形的周长是50厘米,它长的与宽的一样长,这个长方形的面积是多少?
6.修一条路,第一周修多60米,第二周修余下的少40米,还剩320米。求全长多少米?
7.六年级某班有学生55人,选出女同学的参加踢毽子比赛后,剩下的男女生人数恰好相等,求这个班有女同学多少人?
8.一袋大米,用去后,又运来24千克,这时比原来少。求这时多少千克?
9.小明读一本故事书,已读的页数比没读的多,没读的页数比已读的少48页,小明已经读了多少页?
10.阳光小学组织五、六年级同学清理街头小广告。活动统计结果显示:六年级同学清理小广告420则,五年级比六年级少清理。五、六年级同学共清理小广告多少则?
11.五、六年级一共收集了多少个空矿泉水瓶?
12.学校阅览室里有一些同学在阅读课外书,其中女生占总人数的。后来有5名女生离开,这时阅读课外书的女生占。原来阅览室里一共有多少名同学?
13.新华书店运进的科技书是文艺书的,当科技书卖出后,剩下的科技书比文艺书少1251本,运进的科技书有多少本?
14.菜场运来白菜吨,运来的黄瓜是白菜的,运来的黄瓜比萝卜少,运来的萝卜多少吨?
15.苏州体育中心停车场有大、小汽车共145辆,其中大汽车比小汽车多5辆。大、小汽车各有多少辆?
(1)画出线段图。
(2)列式解答。
16.一批零件,甲单独做20小时可以完成,乙单独做30小时可以完成。现在两人合作,完成任务时,甲比乙多做24个。这批零件共有多少个?
17.有甲、乙两个志愿者服务队,甲队有42人,把甲队的调入乙队,这时两队人数一样多。原来甲乙两队共有多少人?
18.小华和小明共有若干本故事书,已知小明的占总数的,若小华给小明10本,则两人的故事书同样多,小华和小明各有多少本故事书?
19.一堆煤36千克,第一天烧了它的,第二天烧了千克,两天共烧了多少千克?
20.某工厂有20吨的煤,第一天用去了,第二天用了剩下的,第二天用去多少吨煤?还剩多少吨煤?
21.六年级同学举行“小发明”比赛,六(1)班上交了40件作品,比六(2)班多交了,六(1)班和六(2)班共交了多少件作品?
22.某班原来男生人数和女生人数是3∶4,后来又转来2名男生,这时男生和全班人数的比是5∶11,现在男、女生人数各是多少?
23.两筐香蕉共重160千克,从第一筐里取出放入第二筐,两筐就一样重。原来两筐香蕉各重多少千克?(先画线段图,再解答)
24.加工一批零件,甲单独做小时完成,乙单独做小时完成,两人合做几小时完成任务的一半?
参考答案:
1.20天
【分析】根据题意,把全部修完需要的天数看成单位“1”,则40天占总天数的,根据分数除法的意义,即可求出总天数,减去已经修的天数即可。
【详解】40÷-40
=60-40
=20(天)
答:修完这条高速公路还要20天。
【点睛】此题考查了分数除法的应用,找准单位“1”,明确已知一个数的几分之几是多少,求这个数用除法。
2.70千米
【分析】根据题意,两车行驶的时间相同,客车的速度是小轿车速度的,所以客车行驶的路程也是小轿车的,把小轿车行驶的路程看作单位“1”,则客车行驶的是,在离中点15千米处相遇,则小轿车比客车多行驶15×2=30千米,对应的分率为(1-),根据分数除法的意义,解答即可。
【详解】15×2÷(1-)
=30÷
=70(千米)
答:相遇时小轿车行驶了70千米。
【点睛】此题考查了相遇问题,分别表示出两车行驶的路程,找出路程差是解题关键。
3.41人
【分析】一位男生上台主持或一位女生上台主持,台下的总人数相等。根据题意,男生上台主持时,台下的男生人数占总人数的;女生上台主持时,台下的男生人数占总人数的,这时的男生人数比刚才多1人。设台下的总人数为x人,根据女生上台时台下男生人数-男生上台时台下男生人数=1,列方程求出台下的总人数,最后加上台上的1人即是这班总人数。
【详解】解 :设台下的总人数为x人。
x-x=1
x-x=1
x=1
x=40
40+1=41(人)
答:这班有41人。
【点睛】本题主要考查比的应用。要理解台下的总人数相等,根据男生上台和女生上台时台下男生的人数变化列方程解答比较简便。
4.300千米
【分析】把A、B两地的距离看作单位“1”,根据题意可知,甲车、乙车每小时总共行全程的,甲车行完全程需要5+3=8小时,甲每小时行全程的,那么乙车每小时行全程的-,再乘8小时求出乙车行全程的分率,再用1减去它,求出剩下全程的分率,它对应的数是120,用除法求出A、B两地相距多少千米。
【详解】5+3=8小时
1-(-)×8
=1-
=
120÷=300(千米)
答:A、B两地相距300千米。
【点睛】解答此题的关键是找清题中的数量间的关系,考查了学生分析解决问题的能力。
5.150平方厘米
【分析】假设长为未知数x厘米,则宽为(50÷2-x)厘米,长的与宽的一样长,据此列出等式解方程求出长和宽,再根据长方形的面积公式求出面积。
【详解】解:设长为x厘米。
x=×(50÷2-x)
x=-x
x+x=
x=
x=15
50÷2-15
=25-15
=10(厘米)
15×10=150(平方厘米)
答:这个长方形的面积是150平方厘米。
【点睛】要熟练掌握长方形的周长和面积公式,用方程解答先找出等量关系,求出长和宽,进而求面积。
6.600米
【分析】由第二周修余下的少40米,还剩320米可知320-40所对应的是修第一周后剩下的,根据已知总量的几分之几是多少,求总量用部分的量除以对应的分率,求出修第一周后的长度,(320-40)÷=420米;第一周修多60米, 420+60对应的就是全长的1-,( 420+60)÷(1-)就是全长。
【详解】[(320-40)÷(1-)+60] ÷(1-)
=[280÷+60] ÷
=[420+60] ÷
=480×
=600(米)
答:全长600米。
【点睛】认真分析题意,找准题中分数的单位“1”,部分的量÷对应的分率=单位“1”的量。
7.30人
【分析】假设这个班女同学有x人,则男同学人数就是(55-x)人,选出女同学的参加踢毽子比赛后,剩下的女同学就是(1-)x,正好和男同学人数相等,据此列出方程解答。
【详解】解:设这个班女同学有x人。
(1-)x=55-x
x=55-x
x+x=55
x=55
x=30
答:这个班有女同学30人。
【点睛】用方程解答此题,关键是找出女同学的和男同学人数相等这个等量关系。
8.280千克
【分析】假设这袋大米有x千克,用去后剩下x,加上24千克后正好是原来的(1-)x,据此列方程解答求出一袋大米的质量,这袋大米的(1-)就是要求的问题。
【详解】解:设这袋大米有x千克。
(1-)x+24=(1-)x
x+24=x
x-x=24
x=24
x=320
320×(1-)
=320×
=280(千克)
答:这时280千克。
【点睛】用方程解答问题要先找出题中的等量关系,有时候不一定直接设要求的问题为未知数。
9.176页
【分析】把没读的页数看作单位“1”,已读的比没读的多,正好多48页,48÷求出没读的页数;已读的页数比没读的多,即已读的是没读的1+,即48的1+,用乘法求出即可。
【详解】48÷=48×=128(页)
128×(1+)
=128×
=176(页)
答:小明已经读了176页。
【点睛】找准单位“1”的量,看另一个量比单位“1”多几分之几,多多少页,用对应的量除以对应的分率求出单位“1”的量,是解题的关键。
10.720则
【分析】根据题意可知,把六年级清理的小广告数量看作“单位1”,则五年级清理小广告的数量为420×=300则,故五、六年级共清理小广告300+420=720则。
【详解】420+420×
=420+420×
=420+300
=720(则)
答:五六年级同学共清理小广告720则。
【点睛】本题主要考查了分数混合运算的应用。解答此类问题要弄清谁是“单位1”以及分率与量的对应关系。
11.360个
【分析】根据题意,把五年级收集的数量看作单位1,则六年级收集的个数是五年级的(1+)。先用五年级收集的个数乘(1+),求出六年级收集的个数,最后再加上五年级的个数即可。
【详解】165+165×(1+)
=165+165×
=165+195
=360(个)
答:五、六年级一共收集了360个空矿泉水瓶。
【点睛】本题考查分数四则混合运算的应用。明确六年级的个数占五年级的分率,从而求出六年级收集的个数是解题的关键。
12.75名
【分析】原来女同学占,则女生是男生人数的,同理可知,阅览室走出5名女生同学后,女生占男生人数的,所以这5名女生占男生人数的-,由此根据分数除法的意义求出男生人数后,即能求出总人数。
【详解】5÷(-)÷(1-)
=5÷(-)÷
=5÷÷
=75(名)
答:原来阅览室里一共有75名同学在看书。
【点睛】明确这一过程中男生人数没有变化,根据女生人数占男生人数分率的变化求出男生有多少人是完成本题的关键。
13.2085本
【分析】将文艺书的本数看成是单位“1”,那么剩下的科技书占文艺的几分之几=新华书店运进的科技书是文艺书的几分之几×(1-卖出几分之几),剩下的科技书比文艺书少几分之几=1-剩下的科技书的本数占文艺书的几分之几,所以运进文艺书的本数=剩下的科技书比文艺书少的本数÷剩下的科技书比文艺书少几分之几,所以运进科技书的本数=运进文艺书的本数×新华书店运进的科技书是文艺书的几分之几,据此代入数据作答即可。
【详解】1-×(1-)
=1-
=
1251÷=2919(本)
2919×=2085(本)
答:运来科技书有2085本。
【点睛】找准单位“1”以及具体数量1251本所对应的分率是解题关键,明确已知一个数的几分之几是多少,求这个数用除法,先求出文艺书的本数是解题关键。
14.吨
【分析】运来萝卜的吨数=运来黄瓜的吨数÷(1-运来的黄瓜比萝卜少几分之几),其中运来黄瓜的吨数=运来白菜的吨数×运来的黄瓜是白菜的几分之几,据此代入数据作答即可。
【详解】×÷(1-)
=
=(吨)
答:运来的萝卜吨。
【点睛】注意两次单位“1”是不同的,求一个数的几分之几用乘法,已知一个数的几分之几求这个数用除法。
15.(1)见详解
(2)45辆;100辆
【分析】先画一条线段表示小汽车的辆数,把它平均分成5份,再画一条线段表示大汽车的辆数,它比小汽车的2份多5辆。以小汽车辆数为单位“1”,把大汽车辆数减去5辆,大汽车辆数就刚好是小汽车的,此时总辆数是(145-5)辆,小汽车辆数占总数的(1+),根据分数除法的意义求出小汽车的辆数,进而求出大汽车的辆数即可。
【详解】(1)
(2)(145-5)÷(1+)
=140÷
=100(辆)
145-100=45(辆)
答:大汽车有45辆,小汽车有100辆。
【点睛】认真分析题意,找出题中单位“1”的量,再看比较量是单位“1”的量的几分之几或几倍,利用和倍问题求出单位“1”的量,注意总和里减去5才是(1+)所对应的量。
16.120个
【分析】把工作总量看作单位“1”,用工作总量÷工作时间=工作效率,分别求出甲、乙的工作效率;再用工作总量÷合作的工作效率之和=合作需要的时间求出合作的时间;完成任务时,甲比乙多做的零件个数24个÷合作的时间=每小时甲比乙多做的零件个数,最后用每小时甲比乙多做的零件个数÷(甲的工效-乙的工效)=这批零件的总个数,据此列式解答。
【详解】1÷(+)
=1÷
=12(小时)
24÷12=2(个)
2÷(-)
=2÷
=120(个)
答:这批零件共有120个。
【点睛】用工作总量除以工作效率之和求出合作时间,然后求出甲比乙每小时多做多少个零件,再用多做的数量除以对应的分率(两人工效之差)求出工作总量是解题的关键。
17.72人
【分析】先用乘法求出甲队的是多少人,即甲队调入乙队的人数,然后用甲队减去调入乙队的人数求出甲队现在的人数(也是乙队现在的人数),两队调动前后人数之和不变,则用甲队现在的人数乘2即可求出原来两队人数之和。
【详解】42×=6(人)
(42-6)×2
=36×2
=72(人)
答:原来甲乙两队共有72人。
【点睛】两队调动前后的人数之和不变,求出现在两队人数之和即是原来的人数之和。先求出甲队的现有人数是解题的关键。
18.80本;60本
【分析】“若小华给小明10本,则两人的故事书同样多”,说明小华原来的故事书比小明多2×10=20(本),小明的占总数的,则小华占总数的1-,比小明多总数的1--,根据分数除法的意义先求出总的本数,再分别求出各自的图书数即可。
【详解】10×2÷(1--)
=20÷
=140(本)
140×=60(本)
140-60=80(本)
答:小明有60本故事书,小华有80本故事书。
【点睛】本题考查了分数的乘法和分数除法的意义,注意解决此类问题中的量率对应关系。比如本题中多的20本对应多的分率1--。
19.3千克
【分析】把这堆煤看作单位“1”,第一天烧了它的,用乘法求出第一天烧的千克数,再加上第二天烧的千克数,即为两天共烧了多少千克。
【详解】36×+
=3+
=3(千克)
答:两天共烧了3千克。
【点睛】此题重在区分分数在具体的题目中的区别:在具体的题目中,带单位是一个具体的数,不带单位是把某一个数量看单位“1”,是它的几分之几。
20.4吨;12吨
【分析】把煤的总量看作单位1,则第一天用去20吨的,用乘法计算求出用去的吨数,继而求出剩下的吨数。第二天用去的是剩下的,继续用乘法求出第二天用去的吨数。用总量减去两天的用量即是剩下的吨数。
【详解】(20-20×)×
=(20-4)×
=16×
=4(吨)
20-20×-4
=20-4-4
=12(吨)
答:第二天用去4吨煤,还剩12吨煤。
【点睛】本题考查分数四则混合运算的实际应用。求一个数的几分之几是多少,用乘法计算。
21.75件
【分析】根据题意,六(1)班比六(2)班多交了,把六(2)班的作品数量看作单位1,则六(1)班的作品数量是六(2)班的(1+),已知六(1)班上交了40件作品,用除法求出单位1即六(2)班的数量。再把两班的数量合起来。
【详解】40÷(1+)+40
=40÷+40
=35+40
=75(件)
答:六(1)班和六(2)班共交了75件作品。
【点睛】本题考查分数四则混合运算的实际应用。已知单位1的几分之几是多少,求单位1,用除法。
22.男生有20人,女生有24人
【分析】把女生人数看作单位“1”,某班原来男生人数和女生人数是3∶4,即原来男生人数占女生人数的,现在男生和全班人数的比是5∶11,这说明女生人数有11-5=6(份),则现在男生人数占女生人数的,所以现在比原来多了女生的-,用2÷(-)即可求出女生人数,进而可以求出现在的男生人数。
【详解】11-5=6(份)
2÷(-)
=2÷(-)
=2÷
=24(人)
24×=20(人)
答:现在男、女生人数各是20人和24人。
【点睛】找准单位“1”和男生人数占女生人数的分率的变化是解题的关键,已知一个数的几分之几是多少,求这个数时用除法计算,求一个数的几分之几是多少时,用乘法计算。
23.第一筐112千克,第二筐48千克。
【分析】首先根据题意,按照线段图的画法及题目中的叙述画出线段图。我们可以把第一筐苹果的重量看作单位“1”,用“1”减去比第二筐多的分率的2倍,可以确定第二筐占第一筐的分率;再结合上述提示,不难得到两筐的重量和占第一筐的分率,然后结合已知,根据分数除法的意义,求出第一筐的重量,接下来用两筐的重量和减去第一筐的重量,即可求出第二筐的重量,从而完成解答。
【详解】线段图如下:
1-×2
=1-
=;
160÷(1+)
=160÷
=160×
=112(千克)
160-112=48(千克)
答:原来第一筐香蕉112千克,第二筐香蕉48千克。
【点睛】从“从第一筐里取出放入第二筐,两筐就一样重”这个关键的条件入手找出之间的等量关系,熟练掌握分数除法的意义,问题就可以迎刃而解。
24.小时
【分析】把这批零件看作单位“1”这批零件的一半就是,则甲的速度=1÷甲单独做完用的时间,乙的速度=1÷乙单独做完用的时间,求两人合做几小时完成任务的一半,直接用除以甲、乙的速度和即可。
【详解】÷(1÷+1÷)
=÷(2+3)
=÷5
=(小时)
答:两人合做完成任务的一半。
【点睛】找准单位“1”是解题的关键,掌握速度、时间和工作总量的关系。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
