26.1.2 反比例函数的图象和性质学案
文档属性
| 名称 | 26.1.2 反比例函数的图象和性质学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 267.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-30 08:25:00 | ||
图片预览


文档简介
“一·三·六”导学案——九年级数学(下)
编号: 班级: 姓名:
课题:反比例函数的图象和性质
主备: 审核: 时间: 年 月 日
【学习目标】
1.体会并了解反比例函数的图象的意义.
2.能描点画出反比例函数的图象.
3.通过对反比例函数的图象的分析,探索并掌握反比例函数的图象和性质.
【自主预习】
学生自主预习教材P4~6,并尝试完成自主预习区.
1、反比例函数的图象是由两条__________组成,它是__________线.
2、反比例函数的图象有如下性质:当k>0时,双曲线的两支分别位于第__________象限,在每一个象限内,y随x的增大而__________;当k<0时,双曲线的两支分别位于第__________象限,在每一个象限内,y随x的增大而__________.
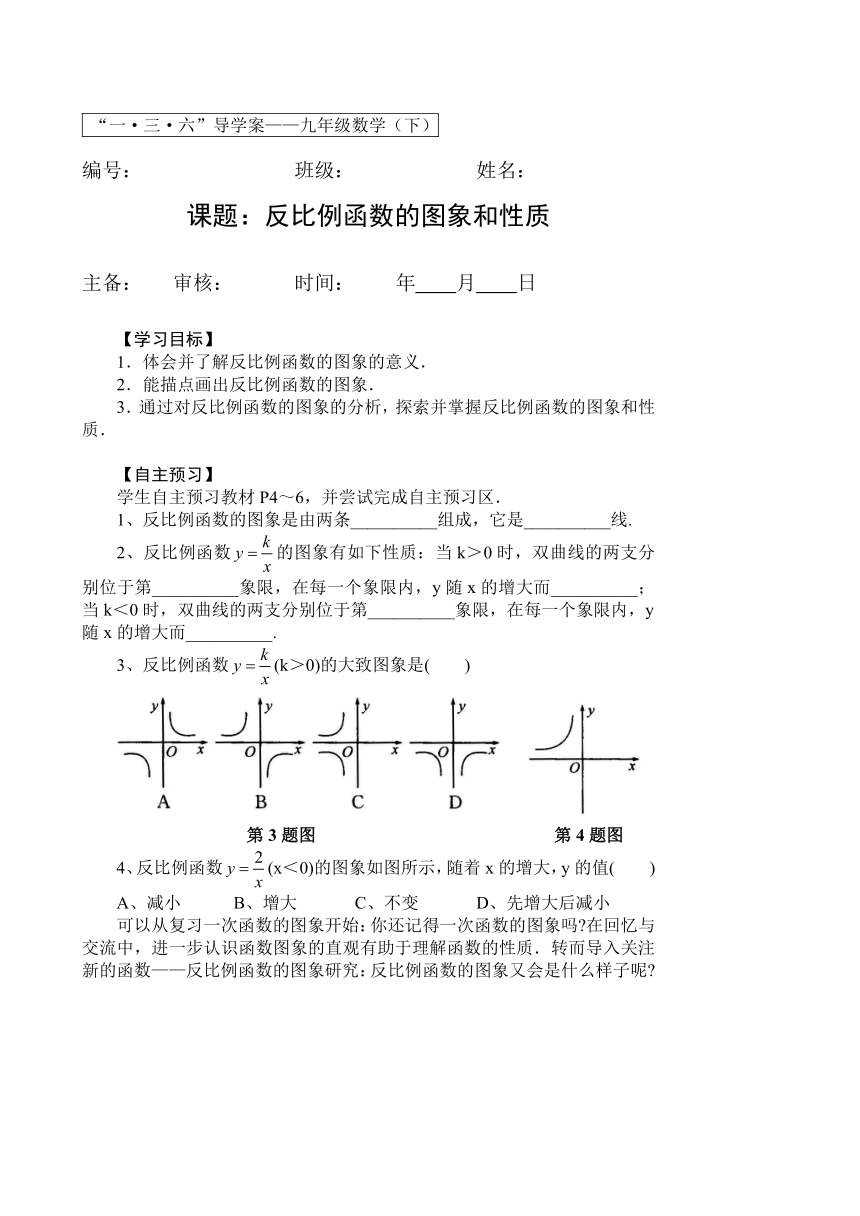
3、反比例函数(k>0)的大致图象是( )
第3题图 第4题图
4、反比例函数(x<0)的图象如图所示,随着x的增大,y的值( )
A、减小 B、增大 C、不变 D、先增大后减小
可以从复习一次函数的图象开始:你还记得一次函数的图象吗 在回忆与交流中,进一步认识函数图象的直观有助于理解函数的性质.转而导入关注新的函数——反比例函数的图象研究:反比例函数的图象又会是什么样子呢
【合作探究】
活动l 反比例函数的图象.
由于反比例函数的图象是曲线型的,且分成两支.对此,学生第一次接触有一定的难度,因此需要分几个层次来探求:
(1)可以先估计——例如:位置(图象所在象限、图象与坐标轴的交点等)、趋势(上升、下降等);
(2)方法与步骤——利用描点作图;
列表:取自变量x的哪些值 ——x是不为零的任何实数,所以不能取x的值为零,但仍可以以零为基准,左右均匀,对称地取值.
描点:依据什么(数据、方法)找点
连线:怎样连线 ——可在各个象限内按照自变量从小到大的顺序用两条光滑的曲线把所描的点连接起来.
活动2 反比例函数的图象.
可以引导学生采用多种方式进行自主探索活动:
(1)可以用画反比例函数的图象的方式与步骤进行自主探索其图象;
(2)可以通过探索函数与之间的关系,画出的图象.
活动3 反比例函数与的图象有什么共同特征
引导学生从通过与一次函数的图象的对比感受反比例函数图象“曲线”及“两支”的特征.
反比例函数(k≠0)的图象是由两个分支组成的曲线.当k>0时,图象在一、三象限;当k<0时,图象在二、四象限.
反比例函数(k≠0)的图象关于直角坐标系的原点成中心对称.
在小组讨论、交流回答的基础上教师投影展示.
反比例函数的图象和性质,并作强调.
图象向上、下、左、右无限靠近坐标轴但与坐标轴无交点(因为k≠0).
【当堂评价】
1.教材P6练习1~2.
2.完成当堂演练区中相应练习.
【拓展提升】
如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)连接AB,在线段DC上是否存在一点E,使△ABE的面积等于5?若存在,求出点E的坐标;若不存在,请说明理由.
【课后检测】
一、选择题
1.一次函数与反比例函数在同一直角坐标系中的大致图象如图所示,则下列判断正确的是( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
第1题图 第3题图 第5题图
2.已知一次函数,y随x的增大而增大,那么反比例函数 ( )
A.在每一象限内,y随x的增大而增大
B.当x<0时,y>0
C.图象在第一、三象限
D.图象在第二、四象限
3.已知一次函数y1=ax+b与反比例函数y2=在同一直角坐标系中的图象如图所示,则当y1A.x<-1或03
C.-13
4.已知A(-1,y1),B(2,y2)两点在双曲线y=上,且y1>y2,则m的取值范围是( )
A.m>0 B.m<0 C.m> D.m<
5.反比趔函数在第一象限的图象如图所示,则k的值可能是 ( )
A.1 B.2 C.3 D.4
二、填空题
1.已知y=(3-4a)xa是反比例函数,则它的图象在__________.
2.已知反比例函数,当13.如果一个正比例函数的图象与反比例函数的图象交于A(x1,y1),B(x2,y2)两点,那么(x2-x1)(y2-y1)的值为__________.
三、解答题
已知反比例函数(k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的解析式;
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(3)当-3【课后反思】
编号: 班级: 姓名:
课题:反比例函数的图象和性质
主备: 审核: 时间: 年 月 日
【学习目标】
1.体会并了解反比例函数的图象的意义.
2.能描点画出反比例函数的图象.
3.通过对反比例函数的图象的分析,探索并掌握反比例函数的图象和性质.
【自主预习】
学生自主预习教材P4~6,并尝试完成自主预习区.
1、反比例函数的图象是由两条__________组成,它是__________线.
2、反比例函数的图象有如下性质:当k>0时,双曲线的两支分别位于第__________象限,在每一个象限内,y随x的增大而__________;当k<0时,双曲线的两支分别位于第__________象限,在每一个象限内,y随x的增大而__________.
3、反比例函数(k>0)的大致图象是( )
第3题图 第4题图
4、反比例函数(x<0)的图象如图所示,随着x的增大,y的值( )
A、减小 B、增大 C、不变 D、先增大后减小
可以从复习一次函数的图象开始:你还记得一次函数的图象吗 在回忆与交流中,进一步认识函数图象的直观有助于理解函数的性质.转而导入关注新的函数——反比例函数的图象研究:反比例函数的图象又会是什么样子呢
【合作探究】
活动l 反比例函数的图象.
由于反比例函数的图象是曲线型的,且分成两支.对此,学生第一次接触有一定的难度,因此需要分几个层次来探求:
(1)可以先估计——例如:位置(图象所在象限、图象与坐标轴的交点等)、趋势(上升、下降等);
(2)方法与步骤——利用描点作图;
列表:取自变量x的哪些值 ——x是不为零的任何实数,所以不能取x的值为零,但仍可以以零为基准,左右均匀,对称地取值.
描点:依据什么(数据、方法)找点
连线:怎样连线 ——可在各个象限内按照自变量从小到大的顺序用两条光滑的曲线把所描的点连接起来.
活动2 反比例函数的图象.
可以引导学生采用多种方式进行自主探索活动:
(1)可以用画反比例函数的图象的方式与步骤进行自主探索其图象;
(2)可以通过探索函数与之间的关系,画出的图象.
活动3 反比例函数与的图象有什么共同特征
引导学生从通过与一次函数的图象的对比感受反比例函数图象“曲线”及“两支”的特征.
反比例函数(k≠0)的图象是由两个分支组成的曲线.当k>0时,图象在一、三象限;当k<0时,图象在二、四象限.
反比例函数(k≠0)的图象关于直角坐标系的原点成中心对称.
在小组讨论、交流回答的基础上教师投影展示.
反比例函数的图象和性质,并作强调.
图象向上、下、左、右无限靠近坐标轴但与坐标轴无交点(因为k≠0).
【当堂评价】
1.教材P6练习1~2.
2.完成当堂演练区中相应练习.
【拓展提升】
如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)连接AB,在线段DC上是否存在一点E,使△ABE的面积等于5?若存在,求出点E的坐标;若不存在,请说明理由.
【课后检测】
一、选择题
1.一次函数与反比例函数在同一直角坐标系中的大致图象如图所示,则下列判断正确的是( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
第1题图 第3题图 第5题图
2.已知一次函数,y随x的增大而增大,那么反比例函数 ( )
A.在每一象限内,y随x的增大而增大
B.当x<0时,y>0
C.图象在第一、三象限
D.图象在第二、四象限
3.已知一次函数y1=ax+b与反比例函数y2=在同一直角坐标系中的图象如图所示,则当y1
C.-1
4.已知A(-1,y1),B(2,y2)两点在双曲线y=上,且y1>y2,则m的取值范围是( )
A.m>0 B.m<0 C.m> D.m<
5.反比趔函数在第一象限的图象如图所示,则k的值可能是 ( )
A.1 B.2 C.3 D.4
二、填空题
1.已知y=(3-4a)xa是反比例函数,则它的图象在__________.
2.已知反比例函数,当1
三、解答题
已知反比例函数(k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的解析式;
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(3)当-3
