29.2由三视图确定几何体的表面积或体积学案
文档属性
| 名称 | 29.2由三视图确定几何体的表面积或体积学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 188.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-30 08:33:25 | ||
图片预览

文档简介
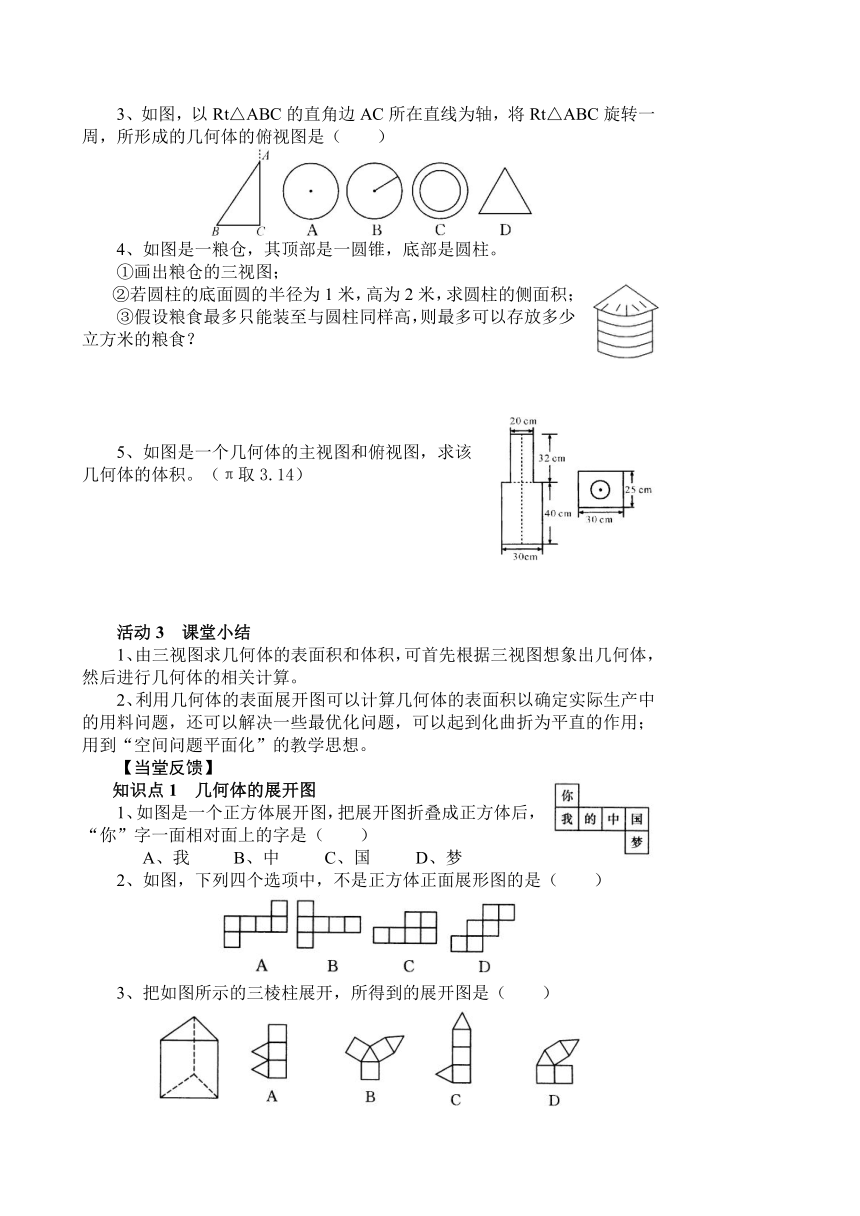
“一·三·六”导学案——九年级数学(下)
编号:2905 班级: 姓名:
课题:由三视图确定几何体的表面积或体积
主备: 审核: 时间:2015年 月 日
【明确目标】
能根据几何体的三视图求几何体的侧面积、表面积、体积等,进而解决实际生活中的面积、体积方面的用料问题。
【自主预习】
阅读教材P99-100,自学“例5”,学会根据三视图确定几何体的形状,并会求其体积问题,解决实际问题。
自学反馈 独立完成后展示学习成果
①圆锥沿它的一条母线剪开的侧面展开图是______________。
②圆柱沿它的一条母线剪开的侧面展开图是______________。
③正方体、长方体的六个面展开的平面图的面积______它的表面积。(填“大于”“小于”或“等于”)
【合作探究】
活动1 小组讨论
例 已知某混凝土管道的三视图,请你按照三视图确定浇灌每段这种管道所需混凝土的方数。(π≈3.14)
活动2 跟踪训练(独立完成后展示学习成果)
1、根据图1、图2几何体的三视图画出它的平面展开图?
2、由如图所示的三视图,求该物体的表面积。
3、如图,以Rt△ABC的直角边AC所在直线为轴,将Rt△ABC旋转一周,所形成的几何体的俯视图是( )
4、如图是一粮仓,其顶部是一圆锥,底部是圆柱。
①画出粮仓的三视图;
②若圆柱的底面圆的半径为1米,高为2米,求圆柱的侧面积;
③假设粮食最多只能装至与圆柱同样高,则最多可以存放多少立方米的粮食?
5、如图是一个几何体的主视图和俯视图,求该几何体的体积。(π取3.14)
活动3 课堂小结
1、由三视图求几何体的表面积和体积,可首先根据三视图想象出几何体,然后进行几何体的相关计算。
2、利用几何体的表面展开图可以计算几何体的表面积以确定实际生产中的用料问题,还可以解决一些最优化问题,可以起到化曲折为平直的作用;用到“空间问题平面化”的教学思想。
【当堂反馈】
知识点1 几何体的展开图
1、如图是一个正方体展开图,把展开图折叠成正方体后,“你”字一面相对面上的字是( )
A、我 B、中 C、国 D、梦
2、如图,下列四个选项中,不是正方体正面展形图的是( )
3、把如图所示的三棱柱展开,所得到的展开图是( )
知识点2 由三视图确定几何体的表面积或体积
4、如图是一个几何体的三视图,则这个几何体的侧面积是( )
A、12π cm2 B、8π cm2 C、6π cm2 D、3π cm2
5、已知某几何体的三视图(单位:cm),则该几何体的侧面积等于( )
A、12π cm2 B、15π cm2 C、24π cm2 D、30π cm2
6、如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是_____。
7、如图,这是一个长方体的主视图和俯视图,由图示数据(单位:cm)可以得出该长方体的体积是_______cm3.
8、下面是某几何体的展开图。
(1)这个几何体的名称是___________;
(2)画出这个几何体的三视图;
(3)求这个几何体的体积。(π取3.14)
【拓展提升】
如图是一个几何体的三视图(单位:厘米)。
(1)写出这个几何体的名称:
(2)根据所示数据计算这个几何体的表面积:
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程。
【课后检测】
1、如图是正方体的一种展开图,其每个面上都标有一个数字,那么在原正方体中,与数字“2”相对的面上的数字是( )
A、1 B、4 C、5 D、6
第1题图 第2题图 第3题图
2、如图是某几何体的三视图,根据图中数据,求得该几何体的体积为( )
A、60π B、70π C、90π D、160π
3、将棱长是1cm的小正方体组成如图所示的几何体,那么这个几何体的表面积是( )
A、36 cm2 B、33 cm2 C、30 cm2 D、27 cm2
4、如图是三个大小不等的正方体拼成的几何体,其中两个较小正方体的棱长之和等于大正方体的棱长,该几何体的主视图、俯视图和左视图的面积分别是S1、S2、S3,则S1、S2、S3的大小关系是( )
A、S1>S2>S3 B、S3>S2>S1 C、S2>S3>S1 D、S1>S3>S2
5、从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为_______.
第4题图 第5题图 第6题图
6、如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积为_________________ cm2.(结果可保留根号)
7、如图是某工件的三视图,求此工件的全面积。
编号:2905 班级: 姓名:
课题:由三视图确定几何体的表面积或体积
主备: 审核: 时间:2015年 月 日
【明确目标】
能根据几何体的三视图求几何体的侧面积、表面积、体积等,进而解决实际生活中的面积、体积方面的用料问题。
【自主预习】
阅读教材P99-100,自学“例5”,学会根据三视图确定几何体的形状,并会求其体积问题,解决实际问题。
自学反馈 独立完成后展示学习成果
①圆锥沿它的一条母线剪开的侧面展开图是______________。
②圆柱沿它的一条母线剪开的侧面展开图是______________。
③正方体、长方体的六个面展开的平面图的面积______它的表面积。(填“大于”“小于”或“等于”)
【合作探究】
活动1 小组讨论
例 已知某混凝土管道的三视图,请你按照三视图确定浇灌每段这种管道所需混凝土的方数。(π≈3.14)
活动2 跟踪训练(独立完成后展示学习成果)
1、根据图1、图2几何体的三视图画出它的平面展开图?
2、由如图所示的三视图,求该物体的表面积。
3、如图,以Rt△ABC的直角边AC所在直线为轴,将Rt△ABC旋转一周,所形成的几何体的俯视图是( )
4、如图是一粮仓,其顶部是一圆锥,底部是圆柱。
①画出粮仓的三视图;
②若圆柱的底面圆的半径为1米,高为2米,求圆柱的侧面积;
③假设粮食最多只能装至与圆柱同样高,则最多可以存放多少立方米的粮食?
5、如图是一个几何体的主视图和俯视图,求该几何体的体积。(π取3.14)
活动3 课堂小结
1、由三视图求几何体的表面积和体积,可首先根据三视图想象出几何体,然后进行几何体的相关计算。
2、利用几何体的表面展开图可以计算几何体的表面积以确定实际生产中的用料问题,还可以解决一些最优化问题,可以起到化曲折为平直的作用;用到“空间问题平面化”的教学思想。
【当堂反馈】
知识点1 几何体的展开图
1、如图是一个正方体展开图,把展开图折叠成正方体后,“你”字一面相对面上的字是( )
A、我 B、中 C、国 D、梦
2、如图,下列四个选项中,不是正方体正面展形图的是( )
3、把如图所示的三棱柱展开,所得到的展开图是( )
知识点2 由三视图确定几何体的表面积或体积
4、如图是一个几何体的三视图,则这个几何体的侧面积是( )
A、12π cm2 B、8π cm2 C、6π cm2 D、3π cm2
5、已知某几何体的三视图(单位:cm),则该几何体的侧面积等于( )
A、12π cm2 B、15π cm2 C、24π cm2 D、30π cm2
6、如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是_____。
7、如图,这是一个长方体的主视图和俯视图,由图示数据(单位:cm)可以得出该长方体的体积是_______cm3.
8、下面是某几何体的展开图。
(1)这个几何体的名称是___________;
(2)画出这个几何体的三视图;
(3)求这个几何体的体积。(π取3.14)
【拓展提升】
如图是一个几何体的三视图(单位:厘米)。
(1)写出这个几何体的名称:
(2)根据所示数据计算这个几何体的表面积:
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程。
【课后检测】
1、如图是正方体的一种展开图,其每个面上都标有一个数字,那么在原正方体中,与数字“2”相对的面上的数字是( )
A、1 B、4 C、5 D、6
第1题图 第2题图 第3题图
2、如图是某几何体的三视图,根据图中数据,求得该几何体的体积为( )
A、60π B、70π C、90π D、160π
3、将棱长是1cm的小正方体组成如图所示的几何体,那么这个几何体的表面积是( )
A、36 cm2 B、33 cm2 C、30 cm2 D、27 cm2
4、如图是三个大小不等的正方体拼成的几何体,其中两个较小正方体的棱长之和等于大正方体的棱长,该几何体的主视图、俯视图和左视图的面积分别是S1、S2、S3,则S1、S2、S3的大小关系是( )
A、S1>S2>S3 B、S3>S2>S1 C、S2>S3>S1 D、S1>S3>S2
5、从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为_______.
第4题图 第5题图 第6题图
6、如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积为_________________ cm2.(结果可保留根号)
7、如图是某工件的三视图,求此工件的全面积。
