29.1 投影(第二课时) 课件(共18张PPT)
文档属性
| 名称 | 29.1 投影(第二课时) 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 720.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-08 09:34:37 | ||
图片预览



文档简介
第29章 投影与视图
29.1 投影
第四单元
第二课时 正投影
复习巩固
探究新知
典例分析
针对训练
归纳小结
布置作业
【提问一】简述投影的概念?
【提问二】投影是如何进行分类的?试举例说明?
一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影.照射光线叫做投影线,投影所在的平面叫做投影面.
平行投影与中心投影
1)平行投影举例:白天旗杆的影子,晷针在晷面上形成的投影;
2)中心投影举例:路灯下行人的影子.
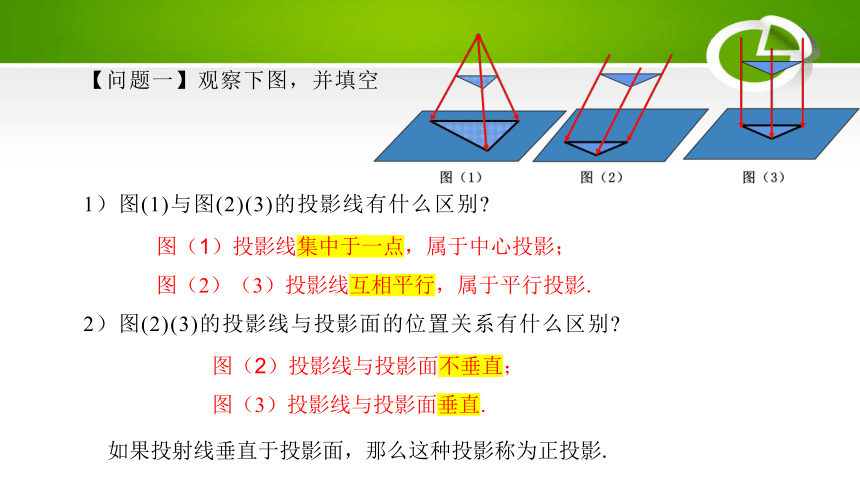
【问题一】观察下图,并填空
1)图(1)与图(2)(3)的投影线有什么区别?
2)图(2)(3)的投影线与投影面的位置关系有什么区别?
图(1)投影线集中于一点,属于中心投影;
图(2)(3)投影线互相平行,属于平行投影.
图(2)投影线与投影面不垂直;
图(3)投影线与投影面垂直.
如果投射线垂直于投影面,那么这种投影称为正投影.
【问题二】由平行投影与正投影的概念,你发现了什么?
1)正投影是特殊的平行投影.
正投影
斜投影
2)平行投影分为斜投影与正投影.
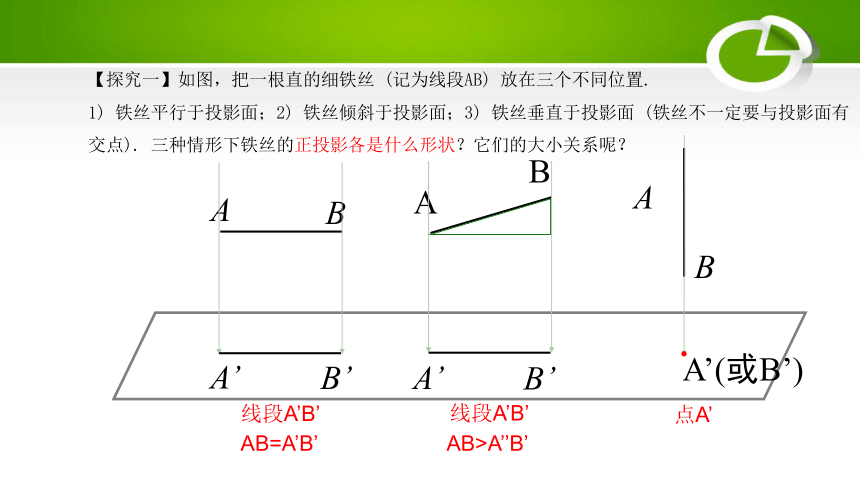
【探究一】如图,把一根直的细铁丝 (记为线段AB) 放在三个不同位置.
1) 铁丝平行于投影面;2) 铁丝倾斜于投影面;3) 铁丝垂直于投影面 (铁丝不一定要与投影面有交点). 三种情形下铁丝的正投影各是什么形状?它们的大小关系呢?
A
B
A
B
A
B
A’
B’
A’
B’
A’(或B’)
线段A’B’
线段A’B’
点A’
AB=A’B’
AB>A’’B’
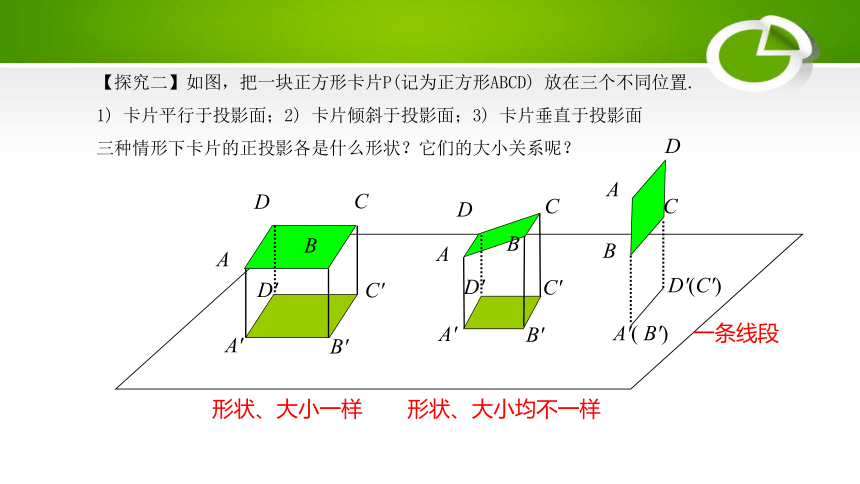
【探究二】如图,把一块正方形卡片P(记为正方形ABCD) 放在三个不同位置.
1) 卡片平行于投影面;2) 卡片倾斜于投影面;3) 卡片垂直于投影面
三种情形下卡片的正投影各是什么形状?它们的大小关系呢?
A
B
C
D
A'
C'
A
B
C
D
A'
B'
C'
D'
A
B
C
D
A'( B')
D'(C')
形状、大小一样
形状、大小均不一样
一条线段
B'
D'
【问题三】简述线段正投影的投影规律?
【问题四】简述平面图形正投影的投影规律?
平行长不变,倾斜长缩短,垂直成一点.
平行形不变,倾斜形改变,垂直成线段.
【探究三】如图,把一个正方体纸盒P(记为正方体ABCDEFGH) 放在两个个不同位置.
纸盒的一个平面ABCD平行于投影面;
纸盒一个面ABCD倾斜于投影面P,底面ADEF垂直于投影面,并且其对角线AE垂直于投影面;
观察两种情形下正方体纸盒的正投影,你发现了什么?
A
B
C
D
A’
B’
C’
D’
A
B
F
D
C
G
D’
C’
F’
G’
A’
B’
物体正投影的形状、大小与它相对于投影面的位置有关.
【问题五】观察线段、平面图形、立体图形的正投影,由此你发现了什么?
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小 完全相同,并且物体正投影的形状、大小与它相对于投影面的位置有关.
例1 下列说法正确的是( )
A.三角形的正投影一定是三角形 B.长方体的正投影一定是长方形
C.球的正投影一定是圆 D.圆锥的正投影一定是三角形
【详解】
A. 三角形的正投影不一定是三角形,错误
B. 长方体的正投影不一定是长方形,错误
C. 球的正投影一定是圆,正确
D. 圆锥的正投影不一定是三角形,错误故选D.
1. 直立在投影面上的圆锥的正投影是 ( )
A.圆 B.三角形 C.矩形 D.正方形
2. 木棒长为2.5m,则它的正投影的长一定( )
A.大于2.5m B.小于2.5m
C.等于2.5m D.小于或等于2.5m
3.如图,长方体的一个底面ABCD在投影面P上,M,N分别是侧棱BF,CG的中点,矩形EFGH与矩形EMNH的投影都是矩形ABCD,设它们的面积分别是S1,S2,S,则S1,S2,S的关系是_____(用“=、>或<”连起来)
S1=S<S2
4.(2022下·广东河源·九年级校考期末)把下列物体与它们的投影连接起来.
5.(2023·湖北恩施·校考模拟预测)物体正投影的形状、大小与它相对于投影面的位置有关.一个三角板的正投影不可能是(?????)
A.一条线段 B.一个与原三角板全等的三角形
C.一个等腰三角形 D.一个小圆点
6.(2022上·山西大同·九年级统考期末)如图,????1????1是线段????????在投影面P上的正投影,????????=10cm,∠????1????????=110°,则投影????1????1的长为(????)
A.10sin70°cm B.10sin20°cm
C.10tan70°cm D.10cos70°cm
?
7. 如图所示,一条线段AB在平面Q内的正投影为A′B′,AB=4m,A′B′=23,则AB
与A′B′的夹角为( )
A.45° B.30° C.60° D.以上都不对
?
【解析】
将线段AB平移,使A点与A′ 点重合,
则在Rt△ABB′ 中,cos∠BAB′=234=32 ,
所以∠BAB′=30°.故本题应选B.
?
8. 已知一纸板的形状为正方形ABCD如图所示.其边长为10厘米,AD、BC与投影面β平行,AB、CD与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1.若∠ABB1=45°,求投影面A1B1C1D1的面积.
【解析】
如图所示,过A作AH⊥BB1于H,
∵∠ABB1=45°,∴△ABH是等腰直角三角形,
∴AH=AB·cos45°=10×22=52 (厘米),.
∴A1B1=AH=52 (厘米),
∵A1D1=AD=10(厘米),
∴矩形A1B1C1D1的面积=A1B1·A1D1=52×10=502 (平方厘米).
?
1.通过本节课的学习,你学会了哪些知识?
2. 简述正投影的概念?
3.简述物体正投影的形状、大小与什么有关?
P92:习题29.1 第3题、第4题、第5题
29.1 投影
第四单元
第二课时 正投影
复习巩固
探究新知
典例分析
针对训练
归纳小结
布置作业
【提问一】简述投影的概念?
【提问二】投影是如何进行分类的?试举例说明?
一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影.照射光线叫做投影线,投影所在的平面叫做投影面.
平行投影与中心投影
1)平行投影举例:白天旗杆的影子,晷针在晷面上形成的投影;
2)中心投影举例:路灯下行人的影子.
【问题一】观察下图,并填空
1)图(1)与图(2)(3)的投影线有什么区别?
2)图(2)(3)的投影线与投影面的位置关系有什么区别?
图(1)投影线集中于一点,属于中心投影;
图(2)(3)投影线互相平行,属于平行投影.
图(2)投影线与投影面不垂直;
图(3)投影线与投影面垂直.
如果投射线垂直于投影面,那么这种投影称为正投影.
【问题二】由平行投影与正投影的概念,你发现了什么?
1)正投影是特殊的平行投影.
正投影
斜投影
2)平行投影分为斜投影与正投影.
【探究一】如图,把一根直的细铁丝 (记为线段AB) 放在三个不同位置.
1) 铁丝平行于投影面;2) 铁丝倾斜于投影面;3) 铁丝垂直于投影面 (铁丝不一定要与投影面有交点). 三种情形下铁丝的正投影各是什么形状?它们的大小关系呢?
A
B
A
B
A
B
A’
B’
A’
B’
A’(或B’)
线段A’B’
线段A’B’
点A’
AB=A’B’
AB>A’’B’
【探究二】如图,把一块正方形卡片P(记为正方形ABCD) 放在三个不同位置.
1) 卡片平行于投影面;2) 卡片倾斜于投影面;3) 卡片垂直于投影面
三种情形下卡片的正投影各是什么形状?它们的大小关系呢?
A
B
C
D
A'
C'
A
B
C
D
A'
B'
C'
D'
A
B
C
D
A'( B')
D'(C')
形状、大小一样
形状、大小均不一样
一条线段
B'
D'
【问题三】简述线段正投影的投影规律?
【问题四】简述平面图形正投影的投影规律?
平行长不变,倾斜长缩短,垂直成一点.
平行形不变,倾斜形改变,垂直成线段.
【探究三】如图,把一个正方体纸盒P(记为正方体ABCDEFGH) 放在两个个不同位置.
纸盒的一个平面ABCD平行于投影面;
纸盒一个面ABCD倾斜于投影面P,底面ADEF垂直于投影面,并且其对角线AE垂直于投影面;
观察两种情形下正方体纸盒的正投影,你发现了什么?
A
B
C
D
A’
B’
C’
D’
A
B
F
D
C
G
D’
C’
F’
G’
A’
B’
物体正投影的形状、大小与它相对于投影面的位置有关.
【问题五】观察线段、平面图形、立体图形的正投影,由此你发现了什么?
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小 完全相同,并且物体正投影的形状、大小与它相对于投影面的位置有关.
例1 下列说法正确的是( )
A.三角形的正投影一定是三角形 B.长方体的正投影一定是长方形
C.球的正投影一定是圆 D.圆锥的正投影一定是三角形
【详解】
A. 三角形的正投影不一定是三角形,错误
B. 长方体的正投影不一定是长方形,错误
C. 球的正投影一定是圆,正确
D. 圆锥的正投影不一定是三角形,错误故选D.
1. 直立在投影面上的圆锥的正投影是 ( )
A.圆 B.三角形 C.矩形 D.正方形
2. 木棒长为2.5m,则它的正投影的长一定( )
A.大于2.5m B.小于2.5m
C.等于2.5m D.小于或等于2.5m
3.如图,长方体的一个底面ABCD在投影面P上,M,N分别是侧棱BF,CG的中点,矩形EFGH与矩形EMNH的投影都是矩形ABCD,设它们的面积分别是S1,S2,S,则S1,S2,S的关系是_____(用“=、>或<”连起来)
S1=S<S2
4.(2022下·广东河源·九年级校考期末)把下列物体与它们的投影连接起来.
5.(2023·湖北恩施·校考模拟预测)物体正投影的形状、大小与它相对于投影面的位置有关.一个三角板的正投影不可能是(?????)
A.一条线段 B.一个与原三角板全等的三角形
C.一个等腰三角形 D.一个小圆点
6.(2022上·山西大同·九年级统考期末)如图,????1????1是线段????????在投影面P上的正投影,????????=10cm,∠????1????????=110°,则投影????1????1的长为(????)
A.10sin70°cm B.10sin20°cm
C.10tan70°cm D.10cos70°cm
?
7. 如图所示,一条线段AB在平面Q内的正投影为A′B′,AB=4m,A′B′=23,则AB
与A′B′的夹角为( )
A.45° B.30° C.60° D.以上都不对
?
【解析】
将线段AB平移,使A点与A′ 点重合,
则在Rt△ABB′ 中,cos∠BAB′=234=32 ,
所以∠BAB′=30°.故本题应选B.
?
8. 已知一纸板的形状为正方形ABCD如图所示.其边长为10厘米,AD、BC与投影面β平行,AB、CD与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1.若∠ABB1=45°,求投影面A1B1C1D1的面积.
【解析】
如图所示,过A作AH⊥BB1于H,
∵∠ABB1=45°,∴△ABH是等腰直角三角形,
∴AH=AB·cos45°=10×22=52 (厘米),.
∴A1B1=AH=52 (厘米),
∵A1D1=AD=10(厘米),
∴矩形A1B1C1D1的面积=A1B1·A1D1=52×10=502 (平方厘米).
?
1.通过本节课的学习,你学会了哪些知识?
2. 简述正投影的概念?
3.简述物体正投影的形状、大小与什么有关?
P92:习题29.1 第3题、第4题、第5题
