第十二章 12.2 三角形全等的判定 2023-2024学年人教版八年级数学上学期课件(71张PPT)
文档属性
| 名称 | 第十二章 12.2 三角形全等的判定 2023-2024学年人教版八年级数学上学期课件(71张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 717.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-08 00:00:00 | ||
图片预览








文档简介
(共71张PPT)
八年级数学·上 新课标 [人]
第十二章 全等三角形
12.2 三角形全等的判定(1)
(1)全等三角形 相等, 相等.
(2)已知△AOC≌△BOD,则∠A=∠B,∠C= ,
AC= ,
=OB,
=OD.
一、探究三角形全等的条件
(1)只给一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗
(2)如果给出两个条件呢 给出两个条件画三角形时,有几种可能的情况,每种情况下作出的三角形一定全等吗
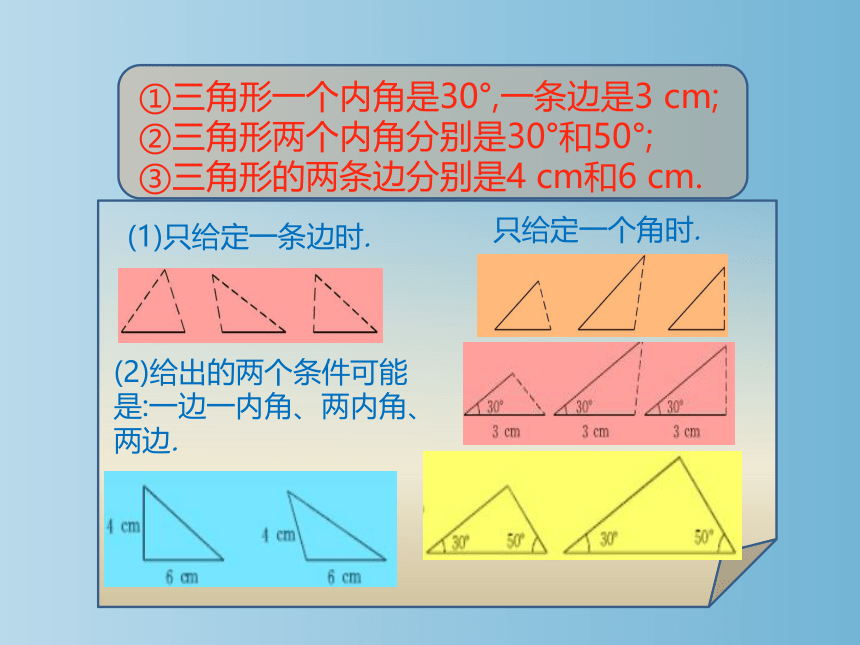
①三角形一个内角是30°,一条边是3 cm;
②三角形两个内角分别是30°和50°;
③三角形的两条边分别是4 cm和6 cm.
(1)只给定一条边时.
只给定一个角时.
(2)给出的两个条件可能
是:一边一内角、两内角、
两边.
如果给出三个条件画三角形时,你能说出有几种情况吗
三条边,两条边一个角,一条边两个角,三个角
用你们准备的4 cm,5 cm,7 cm长的三根细木棒拼一个三角形,与其他同学拼成的三角形比较,它们一定全等吗 你又发现了什么
这些三角形都是全等的.
二、探究运用“SSS”判定两个三角形全等
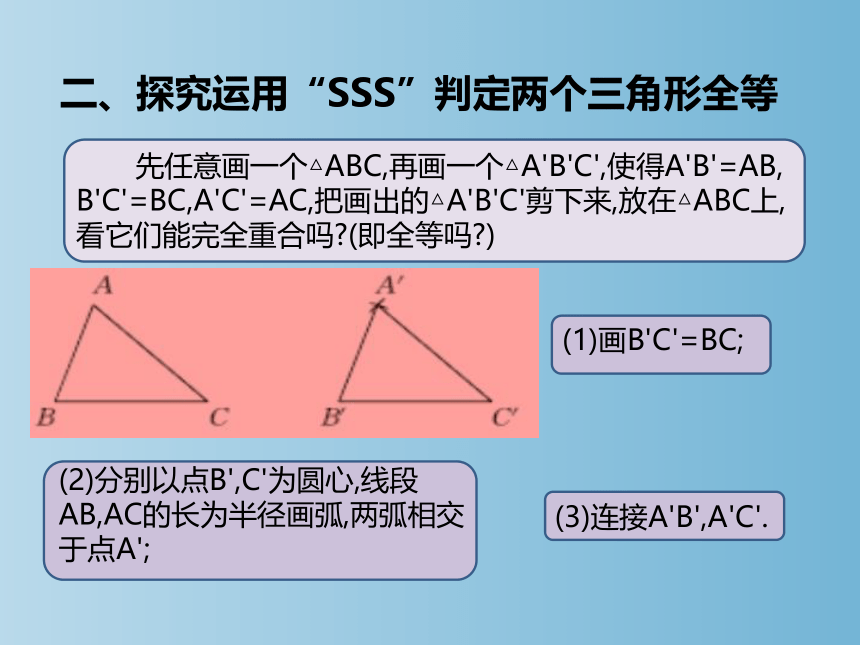
先任意画一个△ABC,再画一个△A'B'C',使得A'B'=AB,
B'C'=BC,A'C'=AC,把画出的△A'B'C'剪下来,放在△ABC上,看它们能完全重合吗 (即全等吗 )
(1)画B'C'=BC;
(3)连接A'B',A'C'.
(2)分别以点B',C'为圆心,线段AB,AC的长为半径画弧,两弧相交于点A';
总结
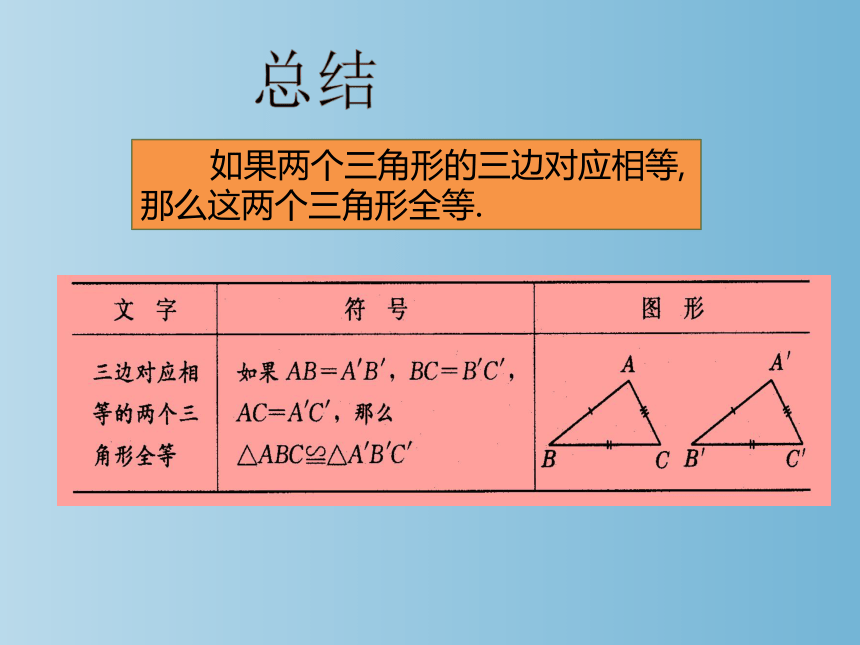
如果两个三角形的三边对应相等,那么这两个三角形全等.
证明:∵D是BC的中点,
∴BD=CD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
例1 在如图所示的三角形钢架中,AB=AC,AD是连接点A与BC中点D的支架.求证△ABD≌△ACD.
如图所示,已知:∠AOB,求作:∠A'O'B',使∠A'O'B'=∠AOB.
三、作一个角等于已知角
如图所示,(1)作射线O'A';
(3)以O‘ 为圆心,以OC的长为半径画弧,交O'A'于点C';
(2)以O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D ;
(5)过D‘作射线O’B‘ ,则∠A'O'B'就是所求作的角.
(4)以点C‘ 为圆心,以CD的长为半径画弧,交前弧于点D';
如果两个三角形的三边对应相等,那么这两个三角形全等,称为“边边边”定理,利用两三角形全等可进行一些相关计算和证明.
知识小结
C
1.如图所示,在△ABC中,AB=AC,BE=CE,则由“SSS”可以判定 ( )
A.△ABD≌△ACD
B.△BDE≌△CDE
C.△ABE≌△ACE
D.以上都不对
EC
△FDB
SSS
2.如图所示,点B,C,D,E在一条直线上,且BC=DE,
AC=FD,AE=FB,则BD= ,△ACE≌ ,理由是 .
3.如图所示,点B,E,C,F在一条直线上,AB=DE,
BE=CF,请添加一个条件: ,使△ABC≌△DEF(SSS).
AC=DF
解:如图所示,连接AC,在△ABC和△ADC中,∴△ABC≌△ADC(SSS),
∴∠B=∠D.
4.如图所示,在四边形ABCD中,AB=AD,CB=CD.求证∠B=∠D.
八年级数学·上 新课标 [人]
第十二章 全等三角形
12.2 全等三角形的判定(2)
(1)怎样的两个三角形是全等三角形 全等三角形的性质是什么 三角形全等的判定方法“SSS”的内容是什么
(2)如果两个三角形有两条边和一个角分别对应相等,那么这两个三角形一定全等吗 此时应该有两种情况,一种是角夹在两条边的中间,形成两边一夹角,一种是角不夹在两边的中间,形成两边一对角,如图所示.
一、“边角边”定理的探究
1.先任意画一个△ABC,再画一个△A'B'C',使A'B'=AB,
A'C'=AC,∠A'=∠A.(即两边和它们的夹角相等)
(3)连接B'C'.
解:如图所示,(1)画∠DA'E=∠A;
(2)在射线A'D上截取A'B'=AB,在射线A'E上截取A'C'=AC;
两边和它们的夹角分别相等的两个三角形全等.简写成“边角边”或“SAS”.
也就是说,三角形的两条边的长度和它们的夹角的大小确定了,这个三角形的形状、大小就确定了.
用符号语言表达为:
在△ABC与△A B C 中,
∴△ABC≌△A B C (SAS)
如果把“两边及其夹角分别相等”改为“两边及其邻角分别相等”,即“两边及其中一边的对角相等”,那么这两个三角形还全等吗
“已知两边及其中一边的对角分别相等的两个三角形全等”不一定成立.
例2 如图所示,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长至D,使CD =CA,连接BC并延长到点E,使CE =CB.连接ED,那么量出DE的长就是A,B的距离.为什么
解析:如果能证明△ABC≌△DEC就可以得出AB=DE.由题意可知△ABC和△DEC具备“边角边”的条件.
∵
∴△ABC≌△DEC(SAS).
证明:在△ABC和△DEC中,
∴AB=DE(全等三角形的对应边相等).
从上例可以看出:因为全等三角形的对应边相等、对应角相等,所以证明线段相等或角相等时,可以通过证明它们是全等三角形的对应边或对应角来解决.
【小结】
两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”.
三角形全等的条件中的相等的角必须是夹角,否则这两个三角形不一定全等,即有两边和其中一边的对角分别相等的两个三角形不一定全等.
C
解析:∵AB∥CD,∴∠A=∠D,又∵AB=CD,AE=FD,
∴△ABE≌△DCF(SAS),∴BE=CF,∠BEA=∠CFD,
∴∠BEF=∠CFE,又∵EF=FE,∴△BEF≌△CFE(SAS),
∴BF=CE,∵AE=DF,∴AE+EF=DF+EF,即AF=DE,∴△ABF≌△DCE(SSS),∴全等三角形共有三对.
1.如图所示,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形有( )
A.1对 B.2对 C.3对 D.4对
解析:两边和它们的夹角分别相等的两个三角形全等(SAS).∠B的两边是AB,BC,∠DEF的两边是DE,EF,而BC=BE+CE,EF=CE+CF,要使BC=EF,则BE=CF.
A
2.如图所示,在△ABC和△DEF中,AB=DE,
∠B=∠DEF,补充下列哪一个条件后,能应用“SAS”判定△ABC≌△DEF ( )
A.BE=CF B.∠ACB=∠DFE
C.AC=DF D.∠A=∠D
解析:已知AB=AC,AD=AE,∠B=∠C不是已知两边的夹角,∴A不可以;∠D=∠E不是已知两边的夹角,∴B不可以;由∠1=∠2得∠BAD=∠CAE,符合“SAS”,可以为补充的条件;∠CAD=∠DAC不是已知两边的夹角,D不可以.
C
3.如图所示,已知AB=AC,AD=AE,欲证△ABD≌△ACE,需补充的条件是 ( )
A.∠B=∠C B.∠D=∠E
C.∠1=∠2 D.∠CAD=∠DAC
4.看图填空.
如图所示,已知BC∥EF,AD=BE,BC=EF.
试说明△ABC≌△DEF.
解:∵AD=BE,
∴ =BE+DB,
即 = .
∵BC∥EF,
∴∠ =∠ (两直线平行,同位角相等).
在△ABC和△DEF中, ,
∴△ABC≌△DEF(SAS).
解析:由AD=BE,利用等式性质可得AB=DE,再由BC∥EF,利用平行线性质可得∠ABC=∠DEF,再加上BC=EF,利用“SAS”说明△ABC≌△DEF.
AB=DE,∠ABC=∠DEF,BC=EF
AD+DB
AB
DE
ABC
DEF
八年级数学·上 新课标 [人]
第十二章 全等三角形
12.2 三角形全等的判定(3)
如图所示,小明不慎把一块三角形的玻璃打碎成四块,现在要去玻璃店去配一块完全一样的玻璃,那么最省事的办法是什么 你能帮小明出出主意吗
一、“角边角”定理的探究
三角形的两个内角分别是60°和80°,它们的夹边为
4 cm,你能画一个三角形同时满足这些条件吗 将你画的三角形剪下,同伴之间相互比较,观察所剪的三角形是不是全等,你能得出什么规律
将所得三角形重叠在一起,发现完全重合,这说明这些三角形全等.
两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).
刚才做的三角形是一个特殊三角形,随意画一个三角形ABC,能不能作一个△A'B'C',使∠A=∠A',∠B=∠B',AB=A'B'呢
如图所示.(1)先用量角器量出∠A与∠B 的度数,再用直尺量出边AB 的长;
(2)画线段A'B',使A'B'=AB ;
(3)分别以A',B' 为顶点,A'B' 为一边在A'B'的同旁作∠DA'B',∠EB'A',使∠DA'B'=∠CAB,∠EB'A'=∠CBA;
(4)射线A'D与B'E 交于一点,记为C', 即可得到△A'B'C'.
将画好的△A'B'C'剪下来,放到△ABC上,发现两个三角形全等.
A'
B'
D
E
C'
两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).这又是一个判定两个三角形全等的方法.
例3 如下图所示,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证AD=AE.
∵
∴△ADC≌△AEB(ASA).
证明:在△ADC和△AEB中,
∴AD=AE.
二、“角角边”定理的探究
如图所示,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,
求证△ABC≌△DEF.
A
B
C
D
E
F
证明:∵∠A+∠B+∠C=∠D+∠E+∠F=180°,
∠A=∠D,∠B=∠E,
∴∠A+∠B=∠D+∠E,
∴∠C=∠F.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
两角和其中一个角的对边分别相等的两个三角形全等(可以简写成“角角边”或“AAS”).
知识点一:“角边角”判定三角形全等.
两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).
这是我们学习的第三个判定三角形全等的方法,这里的两角和夹边,是指同一个三角形的边和角,边是两个角的公共边.
知识点二:“角角边”判定三角形全等.
两角和其中一个角的对边分别相等的两个三角形全等(可以简写成“角角边”或“AAS”).
该判定是通过“ASA”的结论推导得出的,今后可以直接用“AAS”来判定两个三角形全等,它是“ASA”的一个推论.
小结
C
1.如图所示,给出下列四组条件:
①AB=DE,BC=EF,AC=DF;
②AB=DE,∠B=∠E,BC=EF;
③∠B=∠E,BC=EF,∠C=∠F;
④∠B=∠E,∠C=∠F,AC=DE.
其中,能使△ABC≌△DEF 的条件的组数为 ( )
A.1组 B.2组 C.3组 D.4组
D
2.如图所示,在△ABC与△DEF中,给出以下六个条件:
(1)AB=DE ; (2)BC=EF ; (3)AC=DF ;
(4)∠A=∠D ; (5)∠B=∠E ; (6)∠C=∠F.
以其中三个作为已知条件,不能判定△ABC与△DEF全等的是 ( )
A.(1)(5)(2) B.(1)(2)(3)
C.(4)(6)(1) D.(2)(3)(4)
①③④
3.如图所示,已知∠CAE=∠DAB,AC=AD.给出下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的为 .(注:把你认为正确的答案序号都填上)
4.如图所示,已知点E,C,D,A在同一条直线上,
AB∥DF,ED=AB,∠E=∠CPD.求证△ABC≌△DEF.
∴∠E=∠B,
证明:∵AB∥DF,
∴∠B=∠CPD,∠A=∠FDE,
在△ABC和△DEF中,
∴△ABC ≌△DEF(ASA).
八年级数学·上 新课标 [人]
第十二章 全等三角形
12.2 全等三角形(4)
三角形全等的判定方法有哪些
(1)SSS(三边对应相等的两个三角形全等).
(2) ASA(两角和它们的夹边对应相等的两个三角形全等).
(4) AAS(两角和其中一角的对边对应相等的两个三角形全等).
(3) SAS(两边和它们的夹角对应相等的两个三角形全等).
有哪些边角的组合不能判定两个三角形全等 你能通过画图说明理由吗
如图所示,举反例说明了三个角对应相等不能判定两个三角形全等.
SSA不能作为定理的根本原因是什么
是AC不能固定,能够左右摆动.如图所示.
要是我们能使AC只有一种情况,就能证明全等了,应如何办呢
过A作BC的垂线,则AC就只有一种情况.如图所示.
如图所示,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但两个三角形都有一条直角边被花盆遮住无法测量长度.
方法一:测量斜边和一个对应的锐角(AAS);
方法二:测量没遮住的一条直角边和一个对应的锐角(ASA或AAS).
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别相等,于是他就肯定“两个直角三角形是全等的”.你相信他的结论吗
总 结
特殊三角形的直角三角形有特殊的判定方法.
三角形全等的判定方法,说明所有判定方法都适合直角三角形全等的判定.
任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A'B'C',使∠C'=90°,B'C'=BC,A'B'=AB.把画好的Rt△A'B'C'剪下来,放到Rt△ABC上,它们全等吗
画一个Rt△A'B'C',使∠C'=90°,B'C'=BC,A'B'=AB.
一、“斜边、直角边”判定定理的探究
(1)画∠MC'N =90°;
(2)在射线C'M上截取B'C' =BC;
(3)以点B'为圆心,AB为半径画弧,交射线C'N于点A';
(4)连接A'B'.
C'
M
N
C'
M
N
B'
△A'B'C'就是所求作的三角形吗
把画好的△A'B'C'剪下来放在△ABC上,观察这两个三角形是否全等.
方法
判定两个直角三角形全等的一个方法:斜边和一条直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).
欲证BC=AD,首先应寻找和这两条线段有关的三角形,这里有 △ ABD和 △ BAC, △ADO 和△ BCO,其中O为DB,AC的交点,经过对条件的分析,发现 △ ABD和 △ BAC具备全等的条件.
例5 如图所示,AC⊥BC,BD⊥AD,垂足分别为C,D,AC= BD.求证BC=AD.
△
∴∠C与∠D都是直角.
∴Rt△ABC≌Rt△BAD(HL).
证明:∵AC⊥BC, BD⊥AD,
∴BC=AD.
在Rt△ABC和Rt△BAD中,
直角三角形是特殊的三角形,所以不仅能用一般三角形判定全等的方法:
SAS,ASA,AAS,SSS,
还能用直角三角形特殊的判定全等的方法——“HL”.
总 结
斜边和一条直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).
直角三角形首先是三角形,所以一般三角形全等的判定方法都适合它.同时,直角三角形又是特殊的三角形,有它的特殊性,“HL”定理是直角三角形全等独有的判定方法,所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.
小结
D
1.使两个直角三角形全等的条件是 ( )
A.一个锐角对应相等
B.两个锐角对应相等
C.一条边对应相等
D.两条边对应相等
2.如图所示,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD,DF,则图中全等的直角三角形共有( )
A.3对 B.4对
C.5对 D.6对
B
C
3.如图所示,要用“HL”判定Rt△ABC和Rt△DEF全等的条件是 ( )
A.AC=DF,BC=EF B.∠A=∠D,AB=DE
C.AC=DF,AB=DE D.∠B=∠E,BC=EF
4.如图所示,△ABC中,∠ABC=45°,AD⊥BC于D,点E在AD上,且DE=CD,求证BE=AC.
∴AD=BD,
证明:∵∠ABC=45°,
AD⊥BC,
∠BDE=∠ADC=90°.
又∵DE=DC,
∴△BDE≌△ADC.
∴BE=AC.
谢 谢 观 看
八年级数学·上 新课标 [人]
第十二章 全等三角形
12.2 三角形全等的判定(1)
(1)全等三角形 相等, 相等.
(2)已知△AOC≌△BOD,则∠A=∠B,∠C= ,
AC= ,
=OB,
=OD.
一、探究三角形全等的条件
(1)只给一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗
(2)如果给出两个条件呢 给出两个条件画三角形时,有几种可能的情况,每种情况下作出的三角形一定全等吗
①三角形一个内角是30°,一条边是3 cm;
②三角形两个内角分别是30°和50°;
③三角形的两条边分别是4 cm和6 cm.
(1)只给定一条边时.
只给定一个角时.
(2)给出的两个条件可能
是:一边一内角、两内角、
两边.
如果给出三个条件画三角形时,你能说出有几种情况吗
三条边,两条边一个角,一条边两个角,三个角
用你们准备的4 cm,5 cm,7 cm长的三根细木棒拼一个三角形,与其他同学拼成的三角形比较,它们一定全等吗 你又发现了什么
这些三角形都是全等的.
二、探究运用“SSS”判定两个三角形全等
先任意画一个△ABC,再画一个△A'B'C',使得A'B'=AB,
B'C'=BC,A'C'=AC,把画出的△A'B'C'剪下来,放在△ABC上,看它们能完全重合吗 (即全等吗 )
(1)画B'C'=BC;
(3)连接A'B',A'C'.
(2)分别以点B',C'为圆心,线段AB,AC的长为半径画弧,两弧相交于点A';
总结
如果两个三角形的三边对应相等,那么这两个三角形全等.
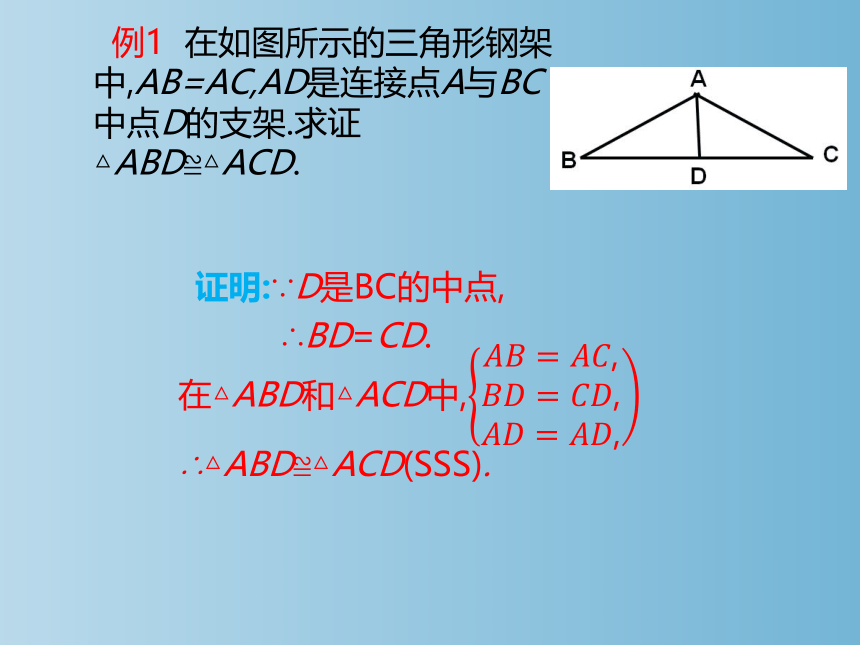
证明:∵D是BC的中点,
∴BD=CD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
例1 在如图所示的三角形钢架中,AB=AC,AD是连接点A与BC中点D的支架.求证△ABD≌△ACD.
如图所示,已知:∠AOB,求作:∠A'O'B',使∠A'O'B'=∠AOB.
三、作一个角等于已知角
如图所示,(1)作射线O'A';
(3)以O‘ 为圆心,以OC的长为半径画弧,交O'A'于点C';
(2)以O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D ;
(5)过D‘作射线O’B‘ ,则∠A'O'B'就是所求作的角.
(4)以点C‘ 为圆心,以CD的长为半径画弧,交前弧于点D';
如果两个三角形的三边对应相等,那么这两个三角形全等,称为“边边边”定理,利用两三角形全等可进行一些相关计算和证明.
知识小结
C
1.如图所示,在△ABC中,AB=AC,BE=CE,则由“SSS”可以判定 ( )
A.△ABD≌△ACD
B.△BDE≌△CDE
C.△ABE≌△ACE
D.以上都不对
EC
△FDB
SSS
2.如图所示,点B,C,D,E在一条直线上,且BC=DE,
AC=FD,AE=FB,则BD= ,△ACE≌ ,理由是 .
3.如图所示,点B,E,C,F在一条直线上,AB=DE,
BE=CF,请添加一个条件: ,使△ABC≌△DEF(SSS).
AC=DF
解:如图所示,连接AC,在△ABC和△ADC中,∴△ABC≌△ADC(SSS),
∴∠B=∠D.
4.如图所示,在四边形ABCD中,AB=AD,CB=CD.求证∠B=∠D.
八年级数学·上 新课标 [人]
第十二章 全等三角形
12.2 全等三角形的判定(2)
(1)怎样的两个三角形是全等三角形 全等三角形的性质是什么 三角形全等的判定方法“SSS”的内容是什么
(2)如果两个三角形有两条边和一个角分别对应相等,那么这两个三角形一定全等吗 此时应该有两种情况,一种是角夹在两条边的中间,形成两边一夹角,一种是角不夹在两边的中间,形成两边一对角,如图所示.
一、“边角边”定理的探究
1.先任意画一个△ABC,再画一个△A'B'C',使A'B'=AB,
A'C'=AC,∠A'=∠A.(即两边和它们的夹角相等)
(3)连接B'C'.
解:如图所示,(1)画∠DA'E=∠A;
(2)在射线A'D上截取A'B'=AB,在射线A'E上截取A'C'=AC;
两边和它们的夹角分别相等的两个三角形全等.简写成“边角边”或“SAS”.
也就是说,三角形的两条边的长度和它们的夹角的大小确定了,这个三角形的形状、大小就确定了.
用符号语言表达为:
在△ABC与△A B C 中,
∴△ABC≌△A B C (SAS)
如果把“两边及其夹角分别相等”改为“两边及其邻角分别相等”,即“两边及其中一边的对角相等”,那么这两个三角形还全等吗
“已知两边及其中一边的对角分别相等的两个三角形全等”不一定成立.
例2 如图所示,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长至D,使CD =CA,连接BC并延长到点E,使CE =CB.连接ED,那么量出DE的长就是A,B的距离.为什么
解析:如果能证明△ABC≌△DEC就可以得出AB=DE.由题意可知△ABC和△DEC具备“边角边”的条件.
∵
∴△ABC≌△DEC(SAS).
证明:在△ABC和△DEC中,
∴AB=DE(全等三角形的对应边相等).
从上例可以看出:因为全等三角形的对应边相等、对应角相等,所以证明线段相等或角相等时,可以通过证明它们是全等三角形的对应边或对应角来解决.
【小结】
两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”.
三角形全等的条件中的相等的角必须是夹角,否则这两个三角形不一定全等,即有两边和其中一边的对角分别相等的两个三角形不一定全等.
C
解析:∵AB∥CD,∴∠A=∠D,又∵AB=CD,AE=FD,
∴△ABE≌△DCF(SAS),∴BE=CF,∠BEA=∠CFD,
∴∠BEF=∠CFE,又∵EF=FE,∴△BEF≌△CFE(SAS),
∴BF=CE,∵AE=DF,∴AE+EF=DF+EF,即AF=DE,∴△ABF≌△DCE(SSS),∴全等三角形共有三对.
1.如图所示,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形有( )
A.1对 B.2对 C.3对 D.4对
解析:两边和它们的夹角分别相等的两个三角形全等(SAS).∠B的两边是AB,BC,∠DEF的两边是DE,EF,而BC=BE+CE,EF=CE+CF,要使BC=EF,则BE=CF.
A
2.如图所示,在△ABC和△DEF中,AB=DE,
∠B=∠DEF,补充下列哪一个条件后,能应用“SAS”判定△ABC≌△DEF ( )
A.BE=CF B.∠ACB=∠DFE
C.AC=DF D.∠A=∠D
解析:已知AB=AC,AD=AE,∠B=∠C不是已知两边的夹角,∴A不可以;∠D=∠E不是已知两边的夹角,∴B不可以;由∠1=∠2得∠BAD=∠CAE,符合“SAS”,可以为补充的条件;∠CAD=∠DAC不是已知两边的夹角,D不可以.
C
3.如图所示,已知AB=AC,AD=AE,欲证△ABD≌△ACE,需补充的条件是 ( )
A.∠B=∠C B.∠D=∠E
C.∠1=∠2 D.∠CAD=∠DAC
4.看图填空.
如图所示,已知BC∥EF,AD=BE,BC=EF.
试说明△ABC≌△DEF.
解:∵AD=BE,
∴ =BE+DB,
即 = .
∵BC∥EF,
∴∠ =∠ (两直线平行,同位角相等).
在△ABC和△DEF中, ,
∴△ABC≌△DEF(SAS).
解析:由AD=BE,利用等式性质可得AB=DE,再由BC∥EF,利用平行线性质可得∠ABC=∠DEF,再加上BC=EF,利用“SAS”说明△ABC≌△DEF.
AB=DE,∠ABC=∠DEF,BC=EF
AD+DB
AB
DE
ABC
DEF
八年级数学·上 新课标 [人]
第十二章 全等三角形
12.2 三角形全等的判定(3)
如图所示,小明不慎把一块三角形的玻璃打碎成四块,现在要去玻璃店去配一块完全一样的玻璃,那么最省事的办法是什么 你能帮小明出出主意吗
一、“角边角”定理的探究
三角形的两个内角分别是60°和80°,它们的夹边为
4 cm,你能画一个三角形同时满足这些条件吗 将你画的三角形剪下,同伴之间相互比较,观察所剪的三角形是不是全等,你能得出什么规律
将所得三角形重叠在一起,发现完全重合,这说明这些三角形全等.
两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).
刚才做的三角形是一个特殊三角形,随意画一个三角形ABC,能不能作一个△A'B'C',使∠A=∠A',∠B=∠B',AB=A'B'呢
如图所示.(1)先用量角器量出∠A与∠B 的度数,再用直尺量出边AB 的长;
(2)画线段A'B',使A'B'=AB ;
(3)分别以A',B' 为顶点,A'B' 为一边在A'B'的同旁作∠DA'B',∠EB'A',使∠DA'B'=∠CAB,∠EB'A'=∠CBA;
(4)射线A'D与B'E 交于一点,记为C', 即可得到△A'B'C'.
将画好的△A'B'C'剪下来,放到△ABC上,发现两个三角形全等.
A'
B'
D
E
C'
两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).这又是一个判定两个三角形全等的方法.
例3 如下图所示,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证AD=AE.
∵
∴△ADC≌△AEB(ASA).
证明:在△ADC和△AEB中,
∴AD=AE.
二、“角角边”定理的探究
如图所示,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,
求证△ABC≌△DEF.
A
B
C
D
E
F
证明:∵∠A+∠B+∠C=∠D+∠E+∠F=180°,
∠A=∠D,∠B=∠E,
∴∠A+∠B=∠D+∠E,
∴∠C=∠F.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
两角和其中一个角的对边分别相等的两个三角形全等(可以简写成“角角边”或“AAS”).
知识点一:“角边角”判定三角形全等.
两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).
这是我们学习的第三个判定三角形全等的方法,这里的两角和夹边,是指同一个三角形的边和角,边是两个角的公共边.
知识点二:“角角边”判定三角形全等.
两角和其中一个角的对边分别相等的两个三角形全等(可以简写成“角角边”或“AAS”).
该判定是通过“ASA”的结论推导得出的,今后可以直接用“AAS”来判定两个三角形全等,它是“ASA”的一个推论.
小结
C
1.如图所示,给出下列四组条件:
①AB=DE,BC=EF,AC=DF;
②AB=DE,∠B=∠E,BC=EF;
③∠B=∠E,BC=EF,∠C=∠F;
④∠B=∠E,∠C=∠F,AC=DE.
其中,能使△ABC≌△DEF 的条件的组数为 ( )
A.1组 B.2组 C.3组 D.4组
D
2.如图所示,在△ABC与△DEF中,给出以下六个条件:
(1)AB=DE ; (2)BC=EF ; (3)AC=DF ;
(4)∠A=∠D ; (5)∠B=∠E ; (6)∠C=∠F.
以其中三个作为已知条件,不能判定△ABC与△DEF全等的是 ( )
A.(1)(5)(2) B.(1)(2)(3)
C.(4)(6)(1) D.(2)(3)(4)
①③④
3.如图所示,已知∠CAE=∠DAB,AC=AD.给出下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的为 .(注:把你认为正确的答案序号都填上)
4.如图所示,已知点E,C,D,A在同一条直线上,
AB∥DF,ED=AB,∠E=∠CPD.求证△ABC≌△DEF.
∴∠E=∠B,
证明:∵AB∥DF,
∴∠B=∠CPD,∠A=∠FDE,
在△ABC和△DEF中,
∴△ABC ≌△DEF(ASA).
八年级数学·上 新课标 [人]
第十二章 全等三角形
12.2 全等三角形(4)
三角形全等的判定方法有哪些
(1)SSS(三边对应相等的两个三角形全等).
(2) ASA(两角和它们的夹边对应相等的两个三角形全等).
(4) AAS(两角和其中一角的对边对应相等的两个三角形全等).
(3) SAS(两边和它们的夹角对应相等的两个三角形全等).
有哪些边角的组合不能判定两个三角形全等 你能通过画图说明理由吗
如图所示,举反例说明了三个角对应相等不能判定两个三角形全等.
SSA不能作为定理的根本原因是什么
是AC不能固定,能够左右摆动.如图所示.
要是我们能使AC只有一种情况,就能证明全等了,应如何办呢
过A作BC的垂线,则AC就只有一种情况.如图所示.
如图所示,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但两个三角形都有一条直角边被花盆遮住无法测量长度.
方法一:测量斜边和一个对应的锐角(AAS);
方法二:测量没遮住的一条直角边和一个对应的锐角(ASA或AAS).
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别相等,于是他就肯定“两个直角三角形是全等的”.你相信他的结论吗
总 结
特殊三角形的直角三角形有特殊的判定方法.
三角形全等的判定方法,说明所有判定方法都适合直角三角形全等的判定.
任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A'B'C',使∠C'=90°,B'C'=BC,A'B'=AB.把画好的Rt△A'B'C'剪下来,放到Rt△ABC上,它们全等吗
画一个Rt△A'B'C',使∠C'=90°,B'C'=BC,A'B'=AB.
一、“斜边、直角边”判定定理的探究
(1)画∠MC'N =90°;
(2)在射线C'M上截取B'C' =BC;
(3)以点B'为圆心,AB为半径画弧,交射线C'N于点A';
(4)连接A'B'.
C'
M
N
C'
M
N
B'
△A'B'C'就是所求作的三角形吗
把画好的△A'B'C'剪下来放在△ABC上,观察这两个三角形是否全等.
方法
判定两个直角三角形全等的一个方法:斜边和一条直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).
欲证BC=AD,首先应寻找和这两条线段有关的三角形,这里有 △ ABD和 △ BAC, △ADO 和△ BCO,其中O为DB,AC的交点,经过对条件的分析,发现 △ ABD和 △ BAC具备全等的条件.
例5 如图所示,AC⊥BC,BD⊥AD,垂足分别为C,D,AC= BD.求证BC=AD.
△
∴∠C与∠D都是直角.
∴Rt△ABC≌Rt△BAD(HL).
证明:∵AC⊥BC, BD⊥AD,
∴BC=AD.
在Rt△ABC和Rt△BAD中,
直角三角形是特殊的三角形,所以不仅能用一般三角形判定全等的方法:
SAS,ASA,AAS,SSS,
还能用直角三角形特殊的判定全等的方法——“HL”.
总 结
斜边和一条直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).
直角三角形首先是三角形,所以一般三角形全等的判定方法都适合它.同时,直角三角形又是特殊的三角形,有它的特殊性,“HL”定理是直角三角形全等独有的判定方法,所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.
小结
D
1.使两个直角三角形全等的条件是 ( )
A.一个锐角对应相等
B.两个锐角对应相等
C.一条边对应相等
D.两条边对应相等
2.如图所示,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD,DF,则图中全等的直角三角形共有( )
A.3对 B.4对
C.5对 D.6对
B
C
3.如图所示,要用“HL”判定Rt△ABC和Rt△DEF全等的条件是 ( )
A.AC=DF,BC=EF B.∠A=∠D,AB=DE
C.AC=DF,AB=DE D.∠B=∠E,BC=EF
4.如图所示,△ABC中,∠ABC=45°,AD⊥BC于D,点E在AD上,且DE=CD,求证BE=AC.
∴AD=BD,
证明:∵∠ABC=45°,
AD⊥BC,
∠BDE=∠ADC=90°.
又∵DE=DC,
∴△BDE≌△ADC.
∴BE=AC.
谢 谢 观 看
