13.3.1等腰三角形 课件 2023-2024学年人教版八年级数学 上册(30张PPT)
文档属性
| 名称 | 13.3.1等腰三角形 课件 2023-2024学年人教版八年级数学 上册(30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 240.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-08 21:54:15 | ||
图片预览






文档简介
(共30张PPT)
八年级数学·上 新课标 [人]
第十三章 轴对称
13.3.1 等腰三角形(1)
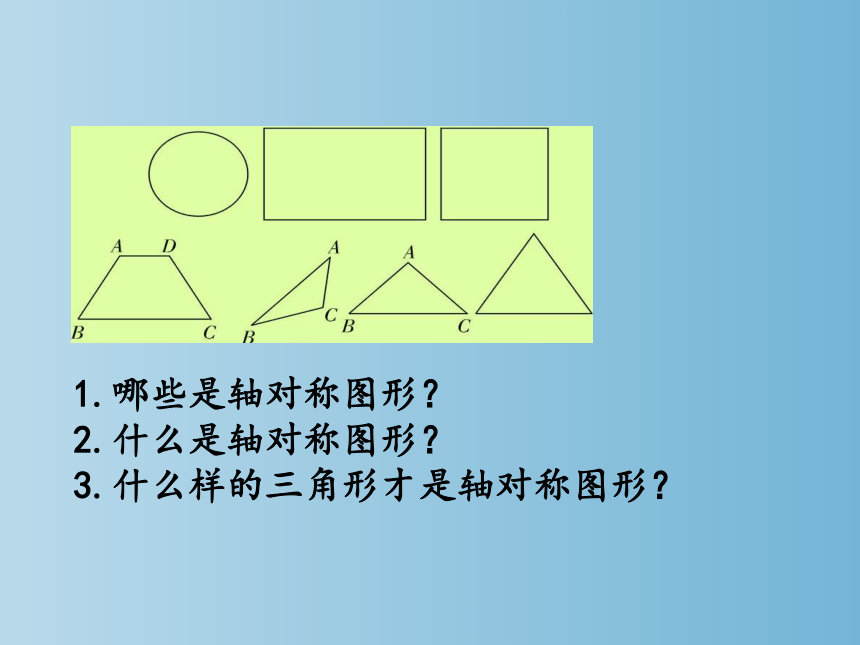
1.哪些是轴对称图形?
2.什么是轴对称图形?
3.什么样的三角形才是轴对称图形?
一、等腰三角形的性质
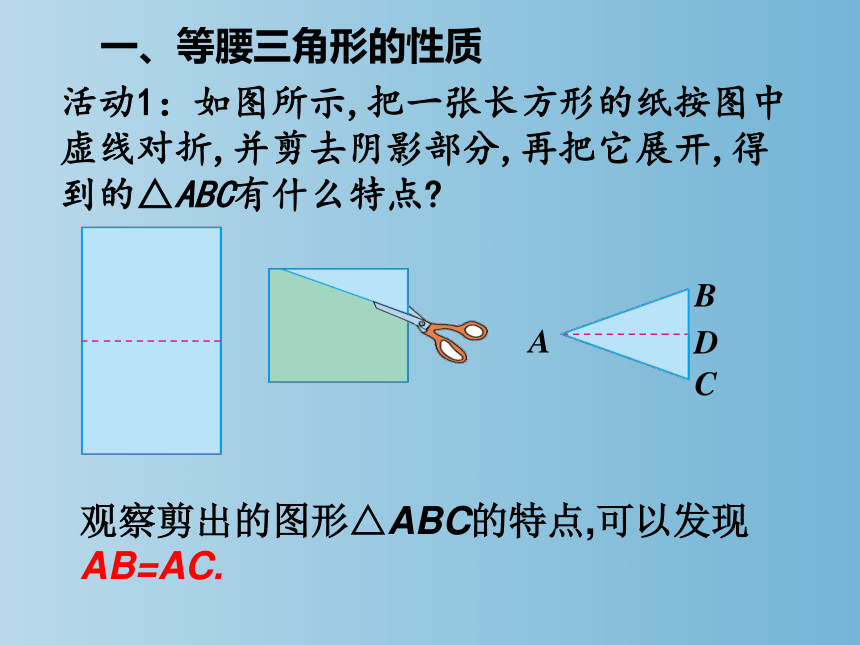
活动1:如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点
A
B
C
D
观察剪出的图形△ABC的特点,可以发现AB=AC.
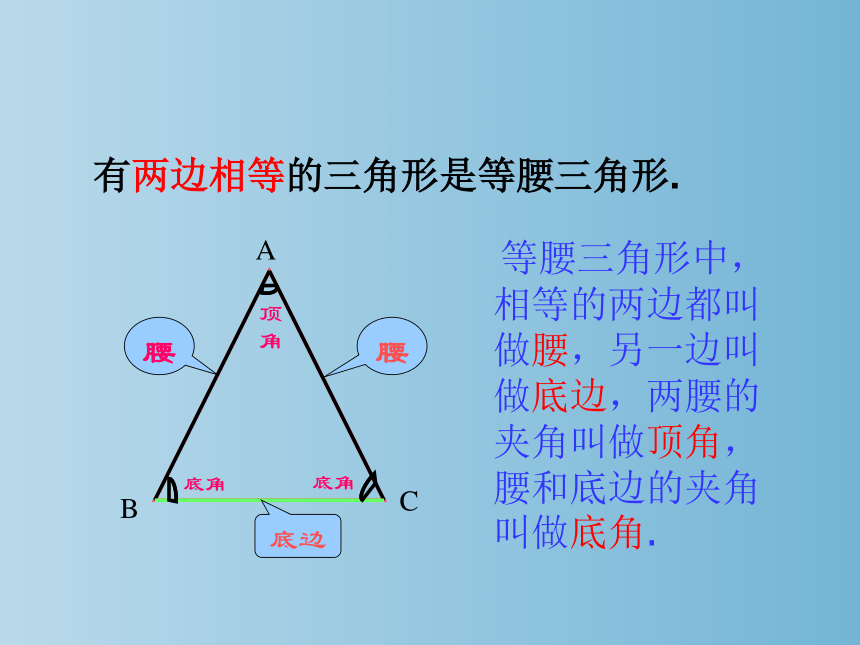
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
有两边相等的三角形是等腰三角形.
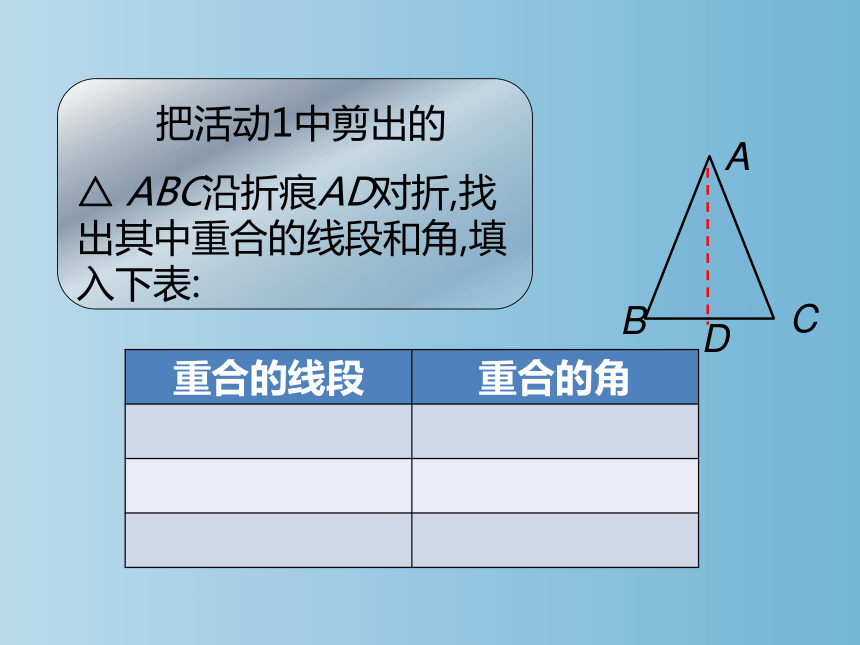
把活动1中剪出的
△ ABC沿折痕AD对折,找出其中重合的线段和角,填入下表:
重合的线段 重合的角
C
B
A
D
性质1 等腰三角形的两个底角相等(简写成“等边对等角”).
性质2 等腰三角形顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”).
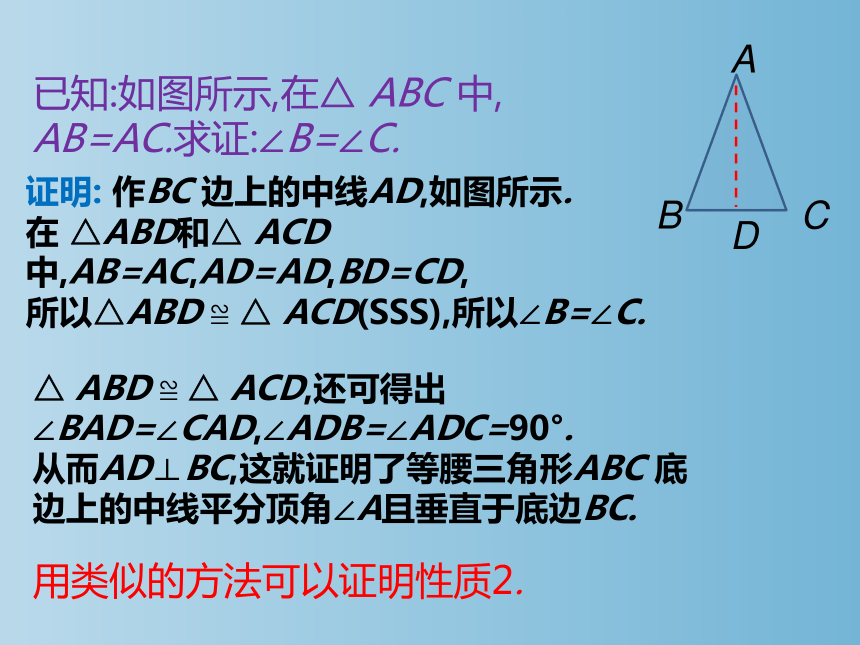
△ ABD ≌ △ ACD,还可得出∠BAD=∠CAD,∠ADB=∠ADC=90°.
从而AD⊥BC,这就证明了等腰三角形ABC 底
边上的中线平分顶角∠A且垂直于底边BC.
用类似的方法可以证明性质2.
C
B
A
D
已知:如图所示,在△ ABC 中,
AB=AC.求证:∠B=∠C.
证明: 作BC 边上的中线AD,如图所示.
在 △ABD和△ ACD 中,AB=AC,AD=AD,BD=CD,
所以△ABD ≌ △ ACD(SSS),所以∠B=∠C.
等腰三角形的对称性
等腰三角形还有以下性质:
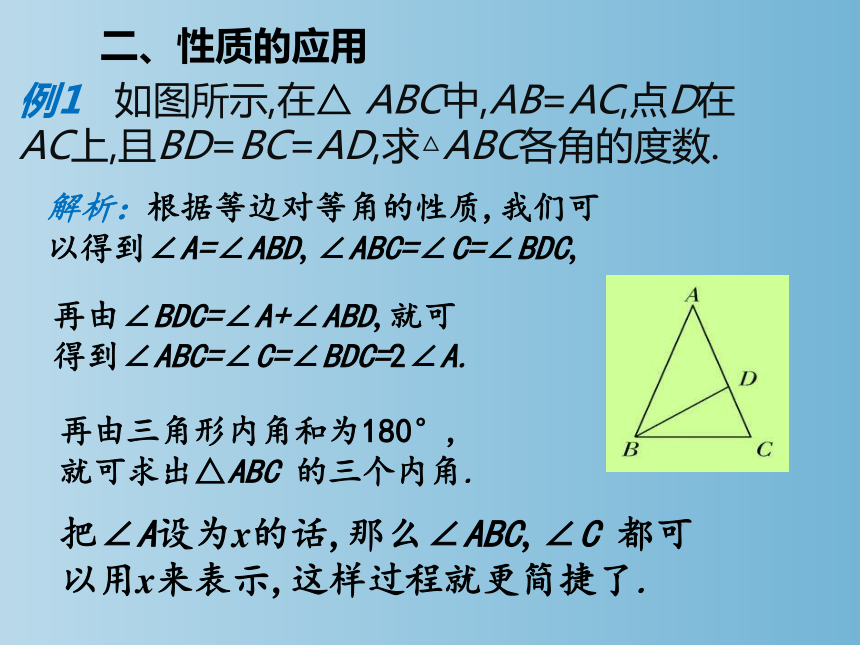
例1 如图所示,在△ ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
二、性质的应用
把∠A设为x的话,那么∠ABC,∠C 都可以用x来表示,这样过程就更简捷了.
解析:根据等边对等角的性质,我们可以得到∠A=∠ABD,∠ABC=∠C=∠BDC,
再由∠BDC=∠A+∠ABD,就可得到∠ABC=∠C=∠BDC=2∠A.
再由三角形内角和为180°,就可求出△ABC 的三个内角.
于是在△ABC中,有:
∠A+∠ABC+∠C=x+2x+2x=180°,
解: 因为AB=AC,BD =BC =AD,
所以∠ABC=∠C =∠BDC,
∠A=∠ABD(等边对等角).
设∠A=x,
则∠BDC=∠A +∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x.
解得x=36°.在△ABC中,∠A=36°,∠ABC=∠C=72°.
小结
1.等腰三角形的性质1:等要三角形的两个底角相等(简写成“等边对等角”).
注意:等边对等角只限于同一个三角形中使用.
2.等腰三角形的性质2:等腰三角形的顶角平分线,底边上的中线,底边上的高相互重合.
说明:等腰三角形是轴对称图形,底边上的中线(底边上的高,顶角平分线)所在的直线是它的对称轴.
D
1.若等腰三角形的顶角为40°,则它的底角度数为 ( )
A.40° B.50° C.60° D.70°
A
2.一个等腰三角形的两边长分别是3和7,则它的周长为 ( )
A.17 B.15 C.13 D.13或17
3.如图所示,在 △ ABC中,AB=AC,AD⊥BC 于点D,若AB=6,CD=4,则△ABC 的周长是 .
20
4.如图所示,在△ABC中,∠A=70°,AB=AC,
CD平分∠ACB,求∠ADC的度数.
∵∠ADC为△BCD的外角,
∴∠ADC=∠B+∠DCB=82.5°.
解:∵在△ABC中,∠A=70°,AB=AC,
∴∠B=∠ACB=55°.
又∵CD平分∠ACB,
∴∠DCB=∠ACD=27.5°.
八年级数学·上 新课标 [人]
第十三章 轴对称
13.3.1 等腰三角形(2)
如图所示,某地质专家为估测一条东西流向河流的宽度,选择河流北岸上一棵树(B点)为地标,然后在这棵树的正南方(南岸A点)插一小旗作标志,沿南偏东60°方向走一段距离到C处时,测得∠ACB为30°,这时,地质专家测得AC的长度就可知河流宽度.
一、等腰三角形的判定方法
如果一个三角形有两条边相等,那么它们所对的角也相等,反过来,如果一个三角形有两个角相等,那么它们所对的边是否相等呢
已知:在△ABC中,∠B=∠C.
求证:AB=AC.
证明:如图所示,作△ABC的角平分线AD.在△BAD和△CAD中,
∴△BAD≌△CAD(AAS),
∴AB=AC.
等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这两个角所对的边也相等,简称“等角对等边”.
说明:三角形的“两边相等”和“两角相等”都是指在同一个三角形中才能得到“等边对等角”及“等角对等边”.“等边对等角”是性质,“等角对等边”是识别方法.
如果一个三形一边上的高、中线和这条边所对的角的平分线中有任意两条线段互相重合,那么这个三角形就是等腰三角形,这种方法是补充的一种方法,可以帮助我们解题时找思路,而在实际的解题过程中往往要转化为识别方法来解决.线段的垂直平分线的性质、角平分线的性质也可以判断相等,从而进一步说明三角形是等腰三角形.
二、判定方法的应用
例2 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知:∠CAE是△ABC的外角,
∠1=∠2,AD∥BC(如图所示).
求证:AB=AC.
证明:∵AD∥BC,
∴∠1=∠B( ),
∠2=∠C( ),
而已知∠1=∠2,
∴∠B=∠C.
∴AB=AC( ).
(1)作线段AB=a.
A
B
M
N
D
C
(3)在MN上取一点C,使DC=h.
(2)作线段AB的垂直平分线MN,与AB相交于点D.
(4)连接AC,BC,则△ABC就是所求作的等腰三角形.
例3 已知等腰三角形底边长为a,底边上的高为h,求作这个等腰三角形.
说明:(1)等腰三角形的判定与性质互逆;
(2)在判定的应用中,可以作底边的高,也可以作顶角平分线,但不能作底边的中线;
(3)判定在同一个三角形中才能适用.
等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
C
1.如图所示,在△ABC中,AB=AC,点D,E在BC边上,∠ABD=∠DAE=∠EAC=36°,则图中共有等腰三角形的个数是 ( )
A.4 B.5 C.6 D.7
D
2.如图所示,一艘海轮位于灯塔P的南偏东70°
方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°方向的N处,则N处与灯塔P的距离为 ( )
A.40海里 B.60海里
C.70海里 D.80海里
C
3.如图所示,已知AB∥CD,BE平分∠ABC,
∠CDE=150°,则∠C等于 ( )
A.150° B.30° C.120° D.60°
谢 谢 观 看
八年级数学·上 新课标 [人]
第十三章 轴对称
13.3.1 等腰三角形(1)
1.哪些是轴对称图形?
2.什么是轴对称图形?
3.什么样的三角形才是轴对称图形?
一、等腰三角形的性质
活动1:如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点
A
B
C
D
观察剪出的图形△ABC的特点,可以发现AB=AC.
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
有两边相等的三角形是等腰三角形.
把活动1中剪出的
△ ABC沿折痕AD对折,找出其中重合的线段和角,填入下表:
重合的线段 重合的角
C
B
A
D
性质1 等腰三角形的两个底角相等(简写成“等边对等角”).
性质2 等腰三角形顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”).
△ ABD ≌ △ ACD,还可得出∠BAD=∠CAD,∠ADB=∠ADC=90°.
从而AD⊥BC,这就证明了等腰三角形ABC 底
边上的中线平分顶角∠A且垂直于底边BC.
用类似的方法可以证明性质2.
C
B
A
D
已知:如图所示,在△ ABC 中,
AB=AC.求证:∠B=∠C.
证明: 作BC 边上的中线AD,如图所示.
在 △ABD和△ ACD 中,AB=AC,AD=AD,BD=CD,
所以△ABD ≌ △ ACD(SSS),所以∠B=∠C.
等腰三角形的对称性
等腰三角形还有以下性质:
例1 如图所示,在△ ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
二、性质的应用
把∠A设为x的话,那么∠ABC,∠C 都可以用x来表示,这样过程就更简捷了.
解析:根据等边对等角的性质,我们可以得到∠A=∠ABD,∠ABC=∠C=∠BDC,
再由∠BDC=∠A+∠ABD,就可得到∠ABC=∠C=∠BDC=2∠A.
再由三角形内角和为180°,就可求出△ABC 的三个内角.
于是在△ABC中,有:
∠A+∠ABC+∠C=x+2x+2x=180°,
解: 因为AB=AC,BD =BC =AD,
所以∠ABC=∠C =∠BDC,
∠A=∠ABD(等边对等角).
设∠A=x,
则∠BDC=∠A +∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x.
解得x=36°.在△ABC中,∠A=36°,∠ABC=∠C=72°.
小结
1.等腰三角形的性质1:等要三角形的两个底角相等(简写成“等边对等角”).
注意:等边对等角只限于同一个三角形中使用.
2.等腰三角形的性质2:等腰三角形的顶角平分线,底边上的中线,底边上的高相互重合.
说明:等腰三角形是轴对称图形,底边上的中线(底边上的高,顶角平分线)所在的直线是它的对称轴.
D
1.若等腰三角形的顶角为40°,则它的底角度数为 ( )
A.40° B.50° C.60° D.70°
A
2.一个等腰三角形的两边长分别是3和7,则它的周长为 ( )
A.17 B.15 C.13 D.13或17
3.如图所示,在 △ ABC中,AB=AC,AD⊥BC 于点D,若AB=6,CD=4,则△ABC 的周长是 .
20
4.如图所示,在△ABC中,∠A=70°,AB=AC,
CD平分∠ACB,求∠ADC的度数.
∵∠ADC为△BCD的外角,
∴∠ADC=∠B+∠DCB=82.5°.
解:∵在△ABC中,∠A=70°,AB=AC,
∴∠B=∠ACB=55°.
又∵CD平分∠ACB,
∴∠DCB=∠ACD=27.5°.
八年级数学·上 新课标 [人]
第十三章 轴对称
13.3.1 等腰三角形(2)
如图所示,某地质专家为估测一条东西流向河流的宽度,选择河流北岸上一棵树(B点)为地标,然后在这棵树的正南方(南岸A点)插一小旗作标志,沿南偏东60°方向走一段距离到C处时,测得∠ACB为30°,这时,地质专家测得AC的长度就可知河流宽度.
一、等腰三角形的判定方法
如果一个三角形有两条边相等,那么它们所对的角也相等,反过来,如果一个三角形有两个角相等,那么它们所对的边是否相等呢
已知:在△ABC中,∠B=∠C.
求证:AB=AC.
证明:如图所示,作△ABC的角平分线AD.在△BAD和△CAD中,
∴△BAD≌△CAD(AAS),
∴AB=AC.
等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这两个角所对的边也相等,简称“等角对等边”.
说明:三角形的“两边相等”和“两角相等”都是指在同一个三角形中才能得到“等边对等角”及“等角对等边”.“等边对等角”是性质,“等角对等边”是识别方法.
如果一个三形一边上的高、中线和这条边所对的角的平分线中有任意两条线段互相重合,那么这个三角形就是等腰三角形,这种方法是补充的一种方法,可以帮助我们解题时找思路,而在实际的解题过程中往往要转化为识别方法来解决.线段的垂直平分线的性质、角平分线的性质也可以判断相等,从而进一步说明三角形是等腰三角形.
二、判定方法的应用
例2 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知:∠CAE是△ABC的外角,
∠1=∠2,AD∥BC(如图所示).
求证:AB=AC.
证明:∵AD∥BC,
∴∠1=∠B( ),
∠2=∠C( ),
而已知∠1=∠2,
∴∠B=∠C.
∴AB=AC( ).
(1)作线段AB=a.
A
B
M
N
D
C
(3)在MN上取一点C,使DC=h.
(2)作线段AB的垂直平分线MN,与AB相交于点D.
(4)连接AC,BC,则△ABC就是所求作的等腰三角形.
例3 已知等腰三角形底边长为a,底边上的高为h,求作这个等腰三角形.
说明:(1)等腰三角形的判定与性质互逆;
(2)在判定的应用中,可以作底边的高,也可以作顶角平分线,但不能作底边的中线;
(3)判定在同一个三角形中才能适用.
等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
C
1.如图所示,在△ABC中,AB=AC,点D,E在BC边上,∠ABD=∠DAE=∠EAC=36°,则图中共有等腰三角形的个数是 ( )
A.4 B.5 C.6 D.7
D
2.如图所示,一艘海轮位于灯塔P的南偏东70°
方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°方向的N处,则N处与灯塔P的距离为 ( )
A.40海里 B.60海里
C.70海里 D.80海里
C
3.如图所示,已知AB∥CD,BE平分∠ABC,
∠CDE=150°,则∠C等于 ( )
A.150° B.30° C.120° D.60°
谢 谢 观 看
