第十三章 13.3.2 等边三角形 人教版八年级数学上学期 课件 (31张PPT)
文档属性
| 名称 | 第十三章 13.3.2 等边三角形 人教版八年级数学上学期 课件 (31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 308.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-08 00:00:00 | ||
图片预览








文档简介
(共31张PPT)
八年级数学·上 新课标 [人]
第十三章 轴对称
13.3.2 等边三角形(1)
这些图片中的物体的设计理念都蕴含着一种特殊的等腰三角形.
一、等边三角形的性质和判定
等腰三角形成为等边三角形的条件.
如果等腰三角形的顶角是60°,那么这个三角形是等边三角形.
根据三角形的内角和定理,顶角是60°,等腰三角形的两个底角的和就是180°-60°=120°,再根据等腰三角形两个底角是相等的,所以每个底角分别是120°÷2=60°,则三个内角分别相等,根据等角对等边,则此时等腰三角形的三条边是相等的,即顶角为60°的等腰三角形为等边三角形.
等腰三角形的底角是60°,那么这个三角形也是等边三角形,同样根据三角形内角和定理和等角对等边的性质.
在等腰三角形中,不论底角是60°,还是顶角是60°,那么这个等腰三角形都是等边三角形.你能用更简洁的语言描述这个结论吗
有一个角是60°的等腰三
角形是等边三角形.
你在与同伴的交流过程中,发现
了什么或受到了何种启示
有一个角是60°在等腰三角形中有两种情况:
(1)这个角是底角;
(2)这个角是顶角.
三角形为等边三角形的条件是什么呢
三个角都
相等的三角形
是等边三角形.
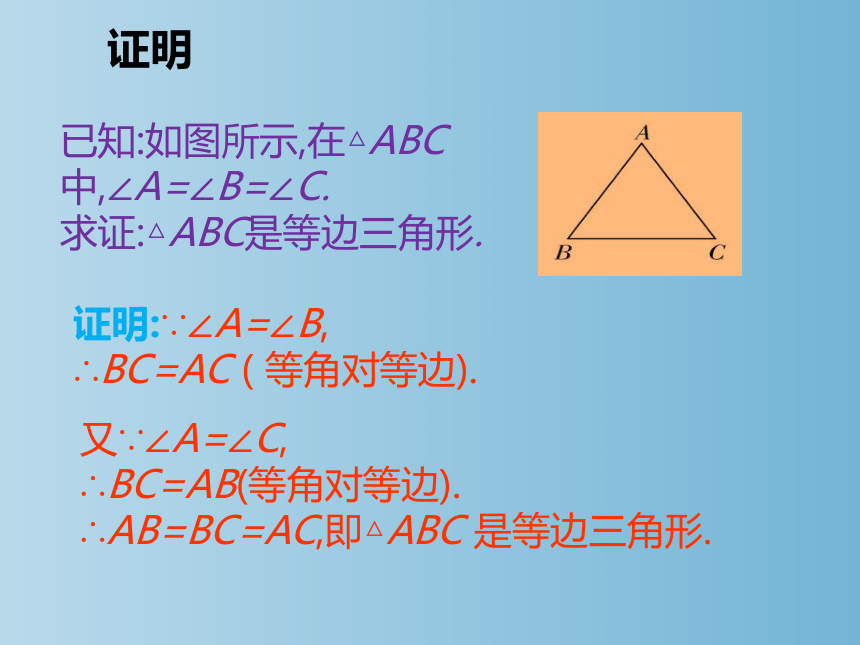
又∵∠A=∠C,
∴BC=AB(等角对等边).
∴AB=BC=AC,即△ABC 是等边三角形.
证明
已知:如图所示,在△ABC 中,∠A=∠B=∠C.
求证:△ABC是等边三角形.
证明:∵∠A=∠B,
∴BC=AC ( 等角对等边).
3.有一个角是60°的等腰三角形是等边三角形.
1.等边三角形的三个内角都相等,并且每一个角都等于60°.
2.三个角都相等的三角形是等边三角形.
在判断一个三角形是否为等边三角形时,我们可从边或角的角度去判断,对于“有一个角是60°的等腰三角形是等边三角形”在使用时应注意,其前提条件必须是“等腰三角形”,此时,不论60°的角是顶角还是底角,都可以说明此三角形是等边三角形.
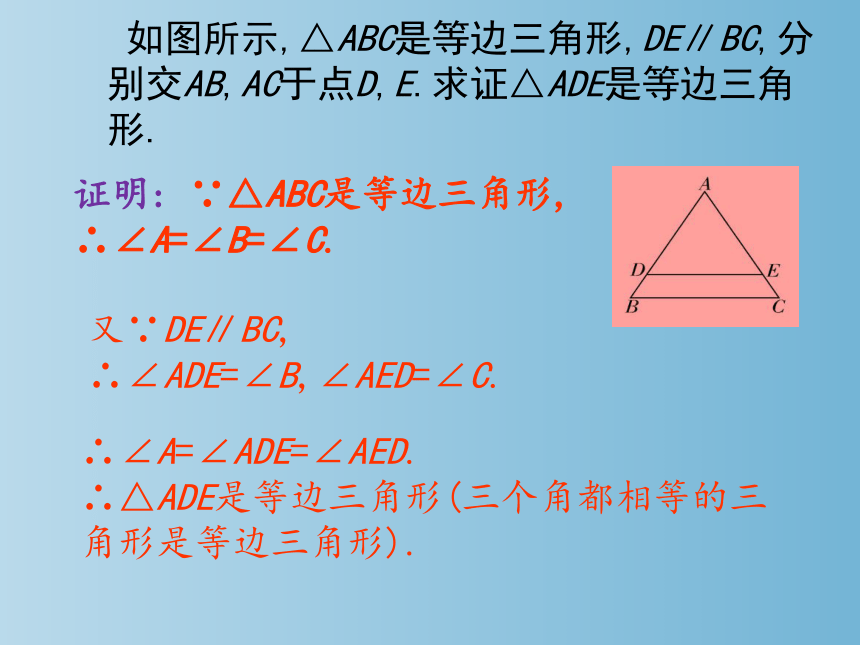
如图所示,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.求证△ADE是等边三角形.
∴∠A=∠ADE=∠AED.
∴△ADE是等边三角形(三个角都相等的三角形是等边三角形).
证明: ∵△ABC是等边三角形,
∴∠A=∠B=∠C.
又∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C.
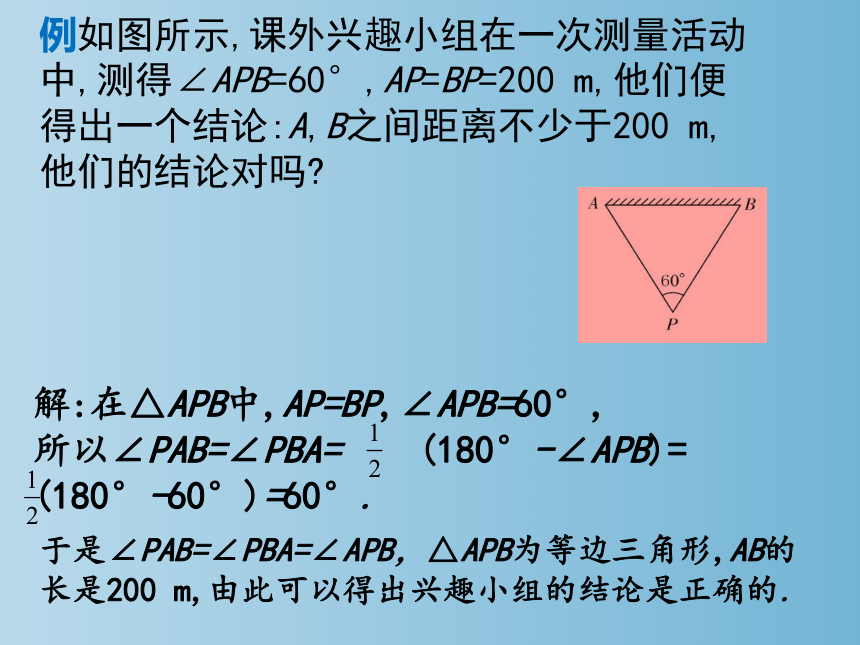
例如图所示,课外兴趣小组在一次测量活动中,测得∠APB=60°,AP=BP=200 m,他们便得出一个结论:A,B之间距离不少于200 m,他们的结论对吗
解:在△APB中,AP=BP,∠APB=60°,
所以∠PAB=∠PBA= (180°-∠APB)= (180°-60°)=60°.
于是∠PAB=∠PBA=∠APB,△APB为等边三角形,AB的长是200 m,由此可以得出兴趣小组的结论是正确的.
1.等边三角形的概念:
三边都相等的三角形是等边三角形.
说明:(1)它可以作为判定一个三角形是否为等边三角形的方法;
(2)可以得出它与等腰三角形的关系:等边三角形是特殊的等腰三角形.在等边三角形中,腰和底、顶角平分线和底角是相对而言的.
小结
2.等边三角形的性质:
三个内角都相等,并且每一个角都等于60°.
说明:等边三角形是轴对称图形,它有三条对称轴;它的任意一角的平分线都垂直平分对边,三边的垂直平分线是对称轴.
3.等边三角形的判定:
(1)三边都相等的三角形是等边三角形.
(2)三个角都相等的三角形是等边三角形.
(3)有一个角是60°的等腰三角形是等边三角形.
A
1.如图所示,过等边三角形ABC的顶点A作射线,若∠1=20°,则∠2的度数是 ( )
A.100° B.80° C.60° D.40°
C
2.如图所示,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是 ( )
A.180° B.220° C.240° D.300°
3.下列三角形:
①有两个角等于60°;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.
其中是等边三角形的有 ( )
A.①②③ B.①②④ C.③ D.①②③④
D
八年级数学·上 新课标 [人]
第十三章 轴对称
13.3.2 等边三角形(2)
将两个含有30°角的直角三角尺摆放在一起,你能借助这个图形,找出Rt△ABC的直角边BC与斜边AB之间的数量关系吗
一、直角三角形的30°角的性质
用含30°角的直角三角尺摆出了如右图所示的两个三角形.
其中,图(1)是等边三角形,因为△ABD≌△ACD,所以AB=AC,又因为Rt△ABD中,∠BAD=30°,所以∠ABD=60°,有一个角是60°的等腰三角形是等边三角形.
图(1)中,∠B=∠C=60°,∠BAC=∠BAD
+∠CAD=30°+30°=60°,所以∠B=∠C=
∠BAC=60°,即△ABC是等边三角形.
由此你能得出在直角三角形中,30°角所对的直角边与斜边的数量关系吗
在直角三角形中,30°角所对直角边是斜边的一半.
证明: 在△ABC 中,∠ACB=90°,
∠BAC=30°,则∠B=60°.
延长BC 至D,使CD=BC,连接AD (如图所示),
B
A
C
D
∵∠ACB=90°,∴∠ACD=90°.
∵AC=AC,
∴△ABC≌△ADC(SAS).
∴AB=AD(全等三角形的对应边相等).
∴△ABD是等边三角形(有一个角是60°的等腰三角形是等边三角形).
∴BC= BD= AB.
已知在Rt△ABC,中, ∠C=90°,∠BAC=30°,求证:BC= AB.
右图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横AC,AB=
7.4 m,∠A=30°.立柱BC,DE要多长
解:因为DE⊥AC,BC⊥AC,∠A=30°,所以BC= AB,DE= AD,所以BC= ×7.4=3.7(m).
又AD= AB,所以DE= AD= ×3.7=1.85(m).
答:立柱BC的长是3.7 m,DE的长是1.85 m.
例等腰三角形的底角为15°,腰长为2a,求腰上的高.如图所示,在△ABC中,AB=AC=2a,∠ABC=∠ACB=15°,CD是腰AB上的高.求CD的长.
解: ∵∠ABC=∠ACB=15°,
∴∠DAC=∠ABC+∠ACB=30°.
在△ADC中,∵CD⊥AD,
∴CD=AC=a ( 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半).
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
说明:此结论是由等边三角形的性质推理得到的,体现了直角三角形的性质,它在解直角三角形的相关问题中常用来求边的长度或角的度数.
小结
C
1.如图所示,AC=BC=10 cm,∠B=15°,
AD⊥BC于点D,则AD的长为 ( )
A.3 cm B.4 cm
C.5 cm D.6 cm
D
2.如图所示,△ABC中,∠C=90°,AC=3,
∠B=30°,点P是BC边上的动点,则AP长不可能是 ( )
A.3.5 B.4.2
C.5.8 D.7
3.已知直角三角形中30°角所对的直角边长是2厘米,则斜边的长是 ( )
A.2厘米 B.4厘米 C.6厘米 D.8厘米
B
谢 谢 观 看
八年级数学·上 新课标 [人]
第十三章 轴对称
13.3.2 等边三角形(1)
这些图片中的物体的设计理念都蕴含着一种特殊的等腰三角形.
一、等边三角形的性质和判定
等腰三角形成为等边三角形的条件.
如果等腰三角形的顶角是60°,那么这个三角形是等边三角形.
根据三角形的内角和定理,顶角是60°,等腰三角形的两个底角的和就是180°-60°=120°,再根据等腰三角形两个底角是相等的,所以每个底角分别是120°÷2=60°,则三个内角分别相等,根据等角对等边,则此时等腰三角形的三条边是相等的,即顶角为60°的等腰三角形为等边三角形.
等腰三角形的底角是60°,那么这个三角形也是等边三角形,同样根据三角形内角和定理和等角对等边的性质.
在等腰三角形中,不论底角是60°,还是顶角是60°,那么这个等腰三角形都是等边三角形.你能用更简洁的语言描述这个结论吗
有一个角是60°的等腰三
角形是等边三角形.
你在与同伴的交流过程中,发现
了什么或受到了何种启示
有一个角是60°在等腰三角形中有两种情况:
(1)这个角是底角;
(2)这个角是顶角.
三角形为等边三角形的条件是什么呢
三个角都
相等的三角形
是等边三角形.
又∵∠A=∠C,
∴BC=AB(等角对等边).
∴AB=BC=AC,即△ABC 是等边三角形.
证明
已知:如图所示,在△ABC 中,∠A=∠B=∠C.
求证:△ABC是等边三角形.
证明:∵∠A=∠B,
∴BC=AC ( 等角对等边).
3.有一个角是60°的等腰三角形是等边三角形.
1.等边三角形的三个内角都相等,并且每一个角都等于60°.
2.三个角都相等的三角形是等边三角形.
在判断一个三角形是否为等边三角形时,我们可从边或角的角度去判断,对于“有一个角是60°的等腰三角形是等边三角形”在使用时应注意,其前提条件必须是“等腰三角形”,此时,不论60°的角是顶角还是底角,都可以说明此三角形是等边三角形.
如图所示,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.求证△ADE是等边三角形.
∴∠A=∠ADE=∠AED.
∴△ADE是等边三角形(三个角都相等的三角形是等边三角形).
证明: ∵△ABC是等边三角形,
∴∠A=∠B=∠C.
又∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C.
例如图所示,课外兴趣小组在一次测量活动中,测得∠APB=60°,AP=BP=200 m,他们便得出一个结论:A,B之间距离不少于200 m,他们的结论对吗
解:在△APB中,AP=BP,∠APB=60°,
所以∠PAB=∠PBA= (180°-∠APB)= (180°-60°)=60°.
于是∠PAB=∠PBA=∠APB,△APB为等边三角形,AB的长是200 m,由此可以得出兴趣小组的结论是正确的.
1.等边三角形的概念:
三边都相等的三角形是等边三角形.
说明:(1)它可以作为判定一个三角形是否为等边三角形的方法;
(2)可以得出它与等腰三角形的关系:等边三角形是特殊的等腰三角形.在等边三角形中,腰和底、顶角平分线和底角是相对而言的.
小结
2.等边三角形的性质:
三个内角都相等,并且每一个角都等于60°.
说明:等边三角形是轴对称图形,它有三条对称轴;它的任意一角的平分线都垂直平分对边,三边的垂直平分线是对称轴.
3.等边三角形的判定:
(1)三边都相等的三角形是等边三角形.
(2)三个角都相等的三角形是等边三角形.
(3)有一个角是60°的等腰三角形是等边三角形.
A
1.如图所示,过等边三角形ABC的顶点A作射线,若∠1=20°,则∠2的度数是 ( )
A.100° B.80° C.60° D.40°
C
2.如图所示,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是 ( )
A.180° B.220° C.240° D.300°
3.下列三角形:
①有两个角等于60°;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.
其中是等边三角形的有 ( )
A.①②③ B.①②④ C.③ D.①②③④
D
八年级数学·上 新课标 [人]
第十三章 轴对称
13.3.2 等边三角形(2)
将两个含有30°角的直角三角尺摆放在一起,你能借助这个图形,找出Rt△ABC的直角边BC与斜边AB之间的数量关系吗
一、直角三角形的30°角的性质
用含30°角的直角三角尺摆出了如右图所示的两个三角形.
其中,图(1)是等边三角形,因为△ABD≌△ACD,所以AB=AC,又因为Rt△ABD中,∠BAD=30°,所以∠ABD=60°,有一个角是60°的等腰三角形是等边三角形.
图(1)中,∠B=∠C=60°,∠BAC=∠BAD
+∠CAD=30°+30°=60°,所以∠B=∠C=
∠BAC=60°,即△ABC是等边三角形.
由此你能得出在直角三角形中,30°角所对的直角边与斜边的数量关系吗
在直角三角形中,30°角所对直角边是斜边的一半.
证明: 在△ABC 中,∠ACB=90°,
∠BAC=30°,则∠B=60°.
延长BC 至D,使CD=BC,连接AD (如图所示),
B
A
C
D
∵∠ACB=90°,∴∠ACD=90°.
∵AC=AC,
∴△ABC≌△ADC(SAS).
∴AB=AD(全等三角形的对应边相等).
∴△ABD是等边三角形(有一个角是60°的等腰三角形是等边三角形).
∴BC= BD= AB.
已知在Rt△ABC,中, ∠C=90°,∠BAC=30°,求证:BC= AB.
右图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横AC,AB=
7.4 m,∠A=30°.立柱BC,DE要多长
解:因为DE⊥AC,BC⊥AC,∠A=30°,所以BC= AB,DE= AD,所以BC= ×7.4=3.7(m).
又AD= AB,所以DE= AD= ×3.7=1.85(m).
答:立柱BC的长是3.7 m,DE的长是1.85 m.
例等腰三角形的底角为15°,腰长为2a,求腰上的高.如图所示,在△ABC中,AB=AC=2a,∠ABC=∠ACB=15°,CD是腰AB上的高.求CD的长.
解: ∵∠ABC=∠ACB=15°,
∴∠DAC=∠ABC+∠ACB=30°.
在△ADC中,∵CD⊥AD,
∴CD=AC=a ( 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半).
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
说明:此结论是由等边三角形的性质推理得到的,体现了直角三角形的性质,它在解直角三角形的相关问题中常用来求边的长度或角的度数.
小结
C
1.如图所示,AC=BC=10 cm,∠B=15°,
AD⊥BC于点D,则AD的长为 ( )
A.3 cm B.4 cm
C.5 cm D.6 cm
D
2.如图所示,△ABC中,∠C=90°,AC=3,
∠B=30°,点P是BC边上的动点,则AP长不可能是 ( )
A.3.5 B.4.2
C.5.8 D.7
3.已知直角三角形中30°角所对的直角边长是2厘米,则斜边的长是 ( )
A.2厘米 B.4厘米 C.6厘米 D.8厘米
B
谢 谢 观 看
