人教版数学 八年级上册13.1.2线段的垂直平分线的性质 课件 (共37张PPT)
文档属性
| 名称 | 人教版数学 八年级上册13.1.2线段的垂直平分线的性质 课件 (共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 412.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-08 21:19:16 | ||
图片预览







文档简介
(共37张PPT)
八年级数学·上 新课标 [人]
第十三章 轴对称
13.1 线段的垂直平分线的性质(1)
为方便居民的出行,准备在小河上修建一座桥.为了让A和B两个社区的居民到桥的距离都相等,建桥的位置应该选在哪
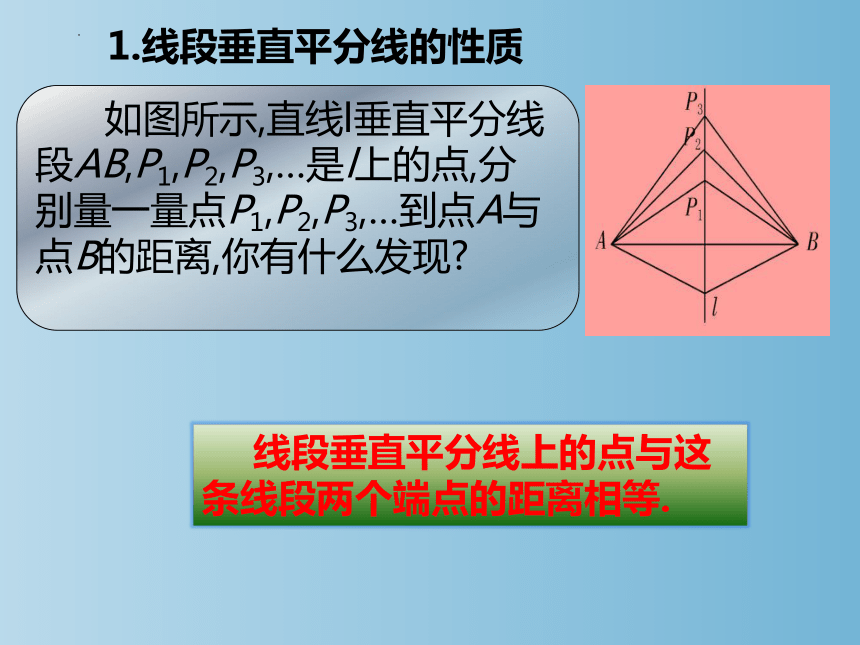
1.线段垂直平分线的性质
线段垂直平分线上的点与这条线段两个端点的距离相等.
如图所示,直线l垂直平分线段AB,P1,P2,P3,…是l上的点,分别量一量点P1,P2,P3,…到点A与点B的距离,你有什么发现
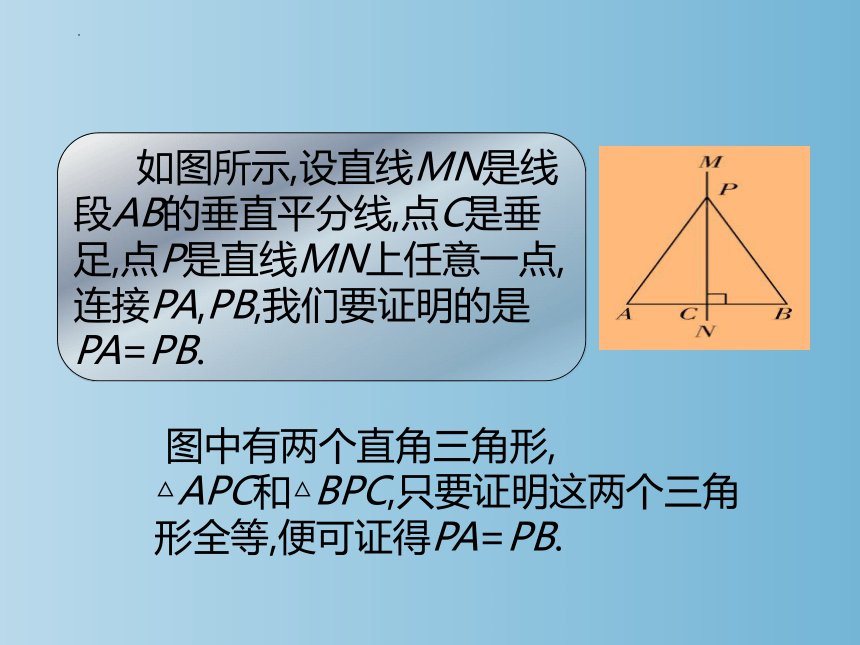
如图所示,设直线MN是线段AB的垂直平分线,点C是垂足,点P是直线MN上任意一点,连接PA,PB,我们要证明的是PA=PB.
图中有两个直角三角形,
△APC和△BPC,只要证明这两个三角形全等,便可证得PA=PB.
已知:MN⊥AB,垂足为点C,AC=BC,点P 是直线MN上任意一点.
求证:PA=PB.
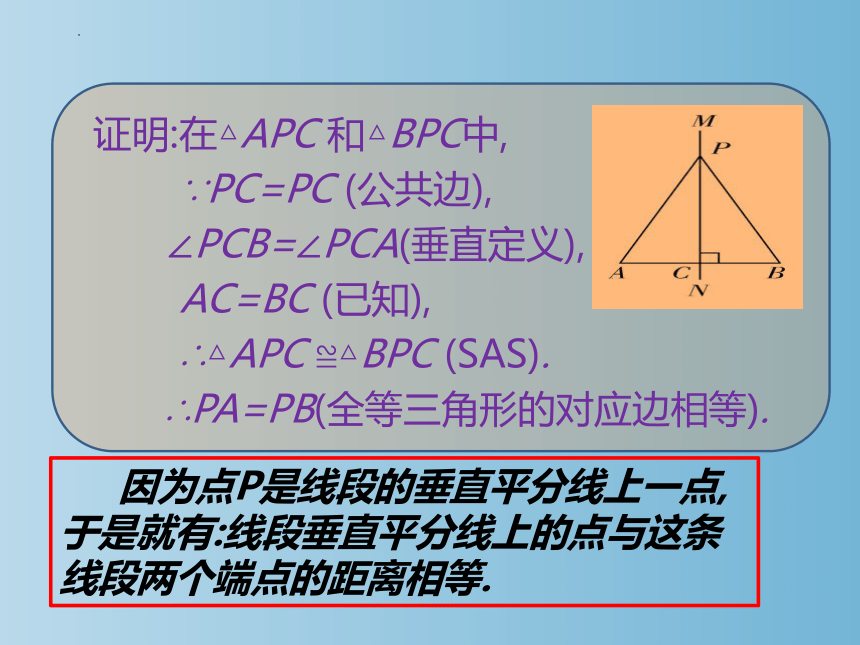
因为点P是线段的垂直平分线上一点,于是就有:线段垂直平分线上的点与这条线段两个端点的距离相等.
证明:在△APC 和△BPC中,
∵PC=PC (公共边),
∠PCB=∠PCA(垂直定义),
AC=BC (已知),
∴△APC ≌△BPC (SAS).
∴PA=PB(全等三角形的对应边相等).
2.线段的垂直平分线的判定
1.你能写出上面这个命题的逆命题吗
2.它是真命题吗
这个命题不是“如果……那么……”的形式,要写出它的逆命题,需分析原命题的条件和结论,将原命题写成“如果……那么……”的形式,逆命题就容易写出.
原命题的条件是“有一个点是线段垂直平分线上的点”,结论是“这个点与这条线段两个端点的距离相等”.
写出逆命题后,就想到判断它的真假.如果真,那么需证明它;如果假,那么需用反例说明.如何证明?
已知:线段AB,点P是平面内一点,且PA=PB.
求证:P点在AB 的垂直平分线上.
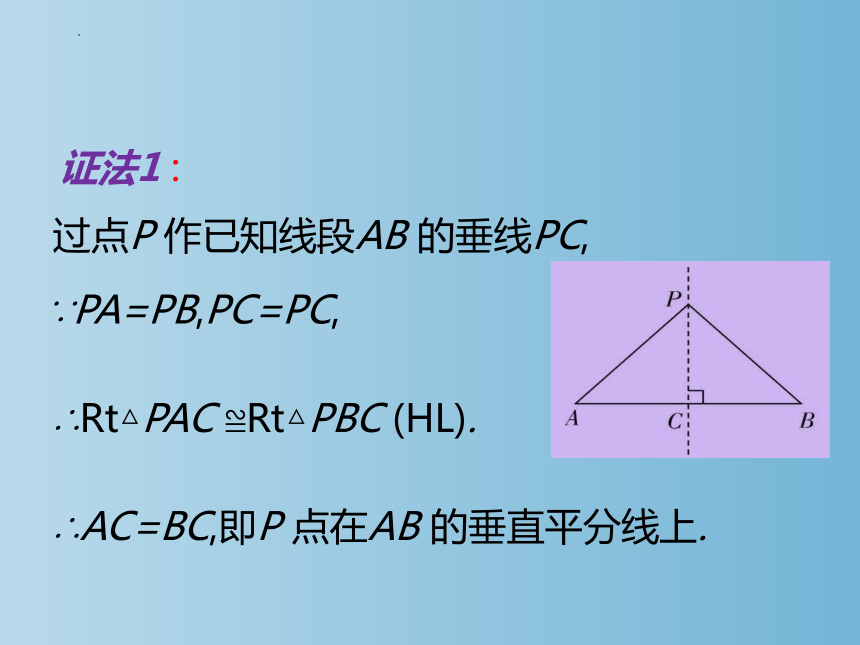
证法1 :
过点P 作已知线段AB 的垂线PC,
∵PA=PB,PC=PC,
∴Rt△PAC ≌Rt△PBC (HL).
∴AC=BC,即P 点在AB 的垂直平分线上.
又∵∠PCA+∠PCB=180°,
∴∠PCA=∠PCB=90°,即PC⊥AB,
∴P点在AB的垂直平分线上.
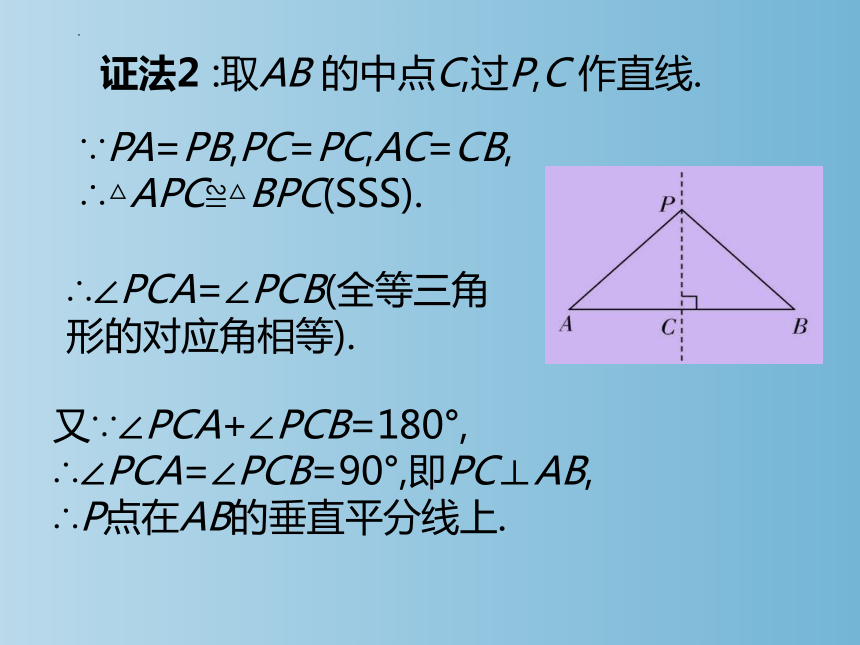
证法2 :取AB 的中点C,过P,C 作直线.
∵PA=PB,PC=PC,AC=CB,
∴△APC≌△BPC(SSS).
∴∠PCA=∠PCB(全等三角形的对应角相等).
证法3 :过P 点作∠APB 的平分线, ∵PA=PB,∠APC=∠BPC,PC=PC,
∴△APC≌△BPC(SAS).
∴AC=BC,∠PCA=∠PCB(全等三角形的对应边相等,对应角相等).
又∵∠PCA+∠PCB=180°,
∴∠PCA=∠PCB=90°,
∴P点在AB的垂直平分线上.
线段的垂直平分线的性质的逆命题是真命题,我们把它称为线段的垂直平分线的判定.
作法:(1)任意取一点K,使点K 和点C 在AB 的两旁.
(2)以点C 为圆心,CK 长为半
径作弧,交AB 于点D 和E.
(4)作直线CF.
直线CF 就是所求作的垂线。
K
C
A
B
D
E
F
尺规作图:经过已知直线外一点作这条直线的垂线.
已知:直线AB 和AB 外一点C (如图所示).
求作:AB 的垂线,使它经过点C.
(3)分别以点D和点E为圆心,大于 DE的长为半径作弧,两弧相交于点F.
小结
1.线段的垂直平分线的判定与性质互为逆命题.
2.线段的垂直平分线的集合定义包含两个意思.
(1)到线段两个端点的距离相等的点都在线段的垂直平分线上.
(2)在线段垂直平分线上的点到线段两个端点的距离相等.
1.如图所示,△ABC中,DE是AC的垂直平分线,AE=4 cm,△ABD的周长为14 cm,则△ABC的周长为 ( )
A.18 cm B.22 cm C.24 cm D.26 cm
B
2.如图所示,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是 ( )
A.AB=AD
B.CA平分∠BCD
C.AB=BD
D.△BEC≌△DEC
C
3.如图所示,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下列结论错误的是 ( )
A.BD平分∠ABC
B.△BCD的周长等于AB+BC
C.AD=BD=BC
D.点D是线段AC的中点
解析:∵在△ABC中,AB=AC,∠A=36°,
∵AB的垂直平分线是DE,∴AD=BD,
∴∠ABD=∠A=36°,∴∠DBC=∠ABC-∠ABD=72°-36°=36°=∠ABD,
∴BD平分∠ABC,故A正确;
△BCD的周长为BC+CD+BD=
BC+CD+AD=BC+AC=BC+AB,故B正确;
∵∠DBC=36°,∠C=72°,∴∠BDC=180°-∠DBC-∠C=72°,∴∠BDC=∠C,∴BD=BC,∴AD=BD=BC,故C正确;
∵BD>CD,∴AD>CD,∴点D不是线段AC的中点,故D错误.
3.如图所示,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下列结论错误的是 ( )
A.BD平分∠ABC
B.△BCD的周长等于AB+BC
C.AD=BD=BC
D.点D是线段AC的中点
D
4.如图所示,已知DE是AC的垂直平分线,AB=
10 cm,BC=11 cm,求△ABD的周长.
解:∵DE垂直平分AC,∴AD=CD,
∴BD+AD=BD+CD=BC=11 cm,
又∵AB=10 cm,
∴△ABD的周长=AB+BC=10+11=21(cm).
八年级数学·上 新课标 [人]
第十三章 轴对称
13.2 线段的垂直平分线的性质(2)
下面的交通标志是轴对称图形吗 如果是轴对称图形,你能找到它的对称轴吗
活动:画对称轴
我们已经学过,如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线,所以我们只要找到两个图形的一对对应点,然后画出以对应点为端点的线段的垂直平分线即可,如何作线段的垂直平分线呢
例2.如图(1)所示,已知点A和点B关于某条直线成轴对称,你能作出这条直线吗
(1)分别以点A,B为圆心,以大于 AB的长为半径作弧(想一想为什么),两弧相交于C,D两点;
(2)作直线CD.
CD就是所求作的直线.
作法(如图所示)
D
C
这个作法实际上就是线段的垂直平分线的尺规作图.
(1)在作法中为什么有CA=CB,DA=DB
(2)可以用这种方法找线段的中点吗 四等分点呢
例(补充).如图所示,△ABC和△A'B'C'是两个成轴对称的图形,请画出它的对称轴.
把问题转化为已解决问题,只要画出点A、点A'连线的垂直平分线即可.
例.图是一个五角星,请画出它的对称轴.
作对称轴的前提是两个图形成轴对称或一个图形是轴对称图形,否则,不存在对称轴。
两个图形成轴对称时,任找一对对应点,作出连接它们的线段的垂直平分线就是对称轴.
对于轴对称图形,由于对称轴可能不是唯一的,因此,要注意选取不同类型的对应点,作出其所有的对称轴.
B
1.正六边形的对称轴有 ( )
A.3条 B.6条 C.9条 D.12条
D
2.如图所示的四角星图形是轴对称图形,它共有对称轴 ( )
A.1条 B.2条 C.3条 D.4条
3.下列图形中,对称轴条数最多的是 ( )
解析:A.如图所示,该图形的对称轴有4条;
B.如图所示,该图形的对称轴有6条;
C.如图所示,该图形的对称轴有3条;
D.如图所示,该图形的对称轴有5条.
综上所述,对称轴条数最多的是B选项.
4.如图所示,作出它们的对称轴.
谢 谢 观 看
八年级数学·上 新课标 [人]
第十三章 轴对称
13.1 线段的垂直平分线的性质(1)
为方便居民的出行,准备在小河上修建一座桥.为了让A和B两个社区的居民到桥的距离都相等,建桥的位置应该选在哪
1.线段垂直平分线的性质
线段垂直平分线上的点与这条线段两个端点的距离相等.
如图所示,直线l垂直平分线段AB,P1,P2,P3,…是l上的点,分别量一量点P1,P2,P3,…到点A与点B的距离,你有什么发现
如图所示,设直线MN是线段AB的垂直平分线,点C是垂足,点P是直线MN上任意一点,连接PA,PB,我们要证明的是PA=PB.
图中有两个直角三角形,
△APC和△BPC,只要证明这两个三角形全等,便可证得PA=PB.
已知:MN⊥AB,垂足为点C,AC=BC,点P 是直线MN上任意一点.
求证:PA=PB.
因为点P是线段的垂直平分线上一点,于是就有:线段垂直平分线上的点与这条线段两个端点的距离相等.
证明:在△APC 和△BPC中,
∵PC=PC (公共边),
∠PCB=∠PCA(垂直定义),
AC=BC (已知),
∴△APC ≌△BPC (SAS).
∴PA=PB(全等三角形的对应边相等).
2.线段的垂直平分线的判定
1.你能写出上面这个命题的逆命题吗
2.它是真命题吗
这个命题不是“如果……那么……”的形式,要写出它的逆命题,需分析原命题的条件和结论,将原命题写成“如果……那么……”的形式,逆命题就容易写出.
原命题的条件是“有一个点是线段垂直平分线上的点”,结论是“这个点与这条线段两个端点的距离相等”.
写出逆命题后,就想到判断它的真假.如果真,那么需证明它;如果假,那么需用反例说明.如何证明?
已知:线段AB,点P是平面内一点,且PA=PB.
求证:P点在AB 的垂直平分线上.
证法1 :
过点P 作已知线段AB 的垂线PC,
∵PA=PB,PC=PC,
∴Rt△PAC ≌Rt△PBC (HL).
∴AC=BC,即P 点在AB 的垂直平分线上.
又∵∠PCA+∠PCB=180°,
∴∠PCA=∠PCB=90°,即PC⊥AB,
∴P点在AB的垂直平分线上.
证法2 :取AB 的中点C,过P,C 作直线.
∵PA=PB,PC=PC,AC=CB,
∴△APC≌△BPC(SSS).
∴∠PCA=∠PCB(全等三角形的对应角相等).
证法3 :过P 点作∠APB 的平分线, ∵PA=PB,∠APC=∠BPC,PC=PC,
∴△APC≌△BPC(SAS).
∴AC=BC,∠PCA=∠PCB(全等三角形的对应边相等,对应角相等).
又∵∠PCA+∠PCB=180°,
∴∠PCA=∠PCB=90°,
∴P点在AB的垂直平分线上.
线段的垂直平分线的性质的逆命题是真命题,我们把它称为线段的垂直平分线的判定.
作法:(1)任意取一点K,使点K 和点C 在AB 的两旁.
(2)以点C 为圆心,CK 长为半
径作弧,交AB 于点D 和E.
(4)作直线CF.
直线CF 就是所求作的垂线。
K
C
A
B
D
E
F
尺规作图:经过已知直线外一点作这条直线的垂线.
已知:直线AB 和AB 外一点C (如图所示).
求作:AB 的垂线,使它经过点C.
(3)分别以点D和点E为圆心,大于 DE的长为半径作弧,两弧相交于点F.
小结
1.线段的垂直平分线的判定与性质互为逆命题.
2.线段的垂直平分线的集合定义包含两个意思.
(1)到线段两个端点的距离相等的点都在线段的垂直平分线上.
(2)在线段垂直平分线上的点到线段两个端点的距离相等.
1.如图所示,△ABC中,DE是AC的垂直平分线,AE=4 cm,△ABD的周长为14 cm,则△ABC的周长为 ( )
A.18 cm B.22 cm C.24 cm D.26 cm
B
2.如图所示,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是 ( )
A.AB=AD
B.CA平分∠BCD
C.AB=BD
D.△BEC≌△DEC
C
3.如图所示,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下列结论错误的是 ( )
A.BD平分∠ABC
B.△BCD的周长等于AB+BC
C.AD=BD=BC
D.点D是线段AC的中点
解析:∵在△ABC中,AB=AC,∠A=36°,
∵AB的垂直平分线是DE,∴AD=BD,
∴∠ABD=∠A=36°,∴∠DBC=∠ABC-∠ABD=72°-36°=36°=∠ABD,
∴BD平分∠ABC,故A正确;
△BCD的周长为BC+CD+BD=
BC+CD+AD=BC+AC=BC+AB,故B正确;
∵∠DBC=36°,∠C=72°,∴∠BDC=180°-∠DBC-∠C=72°,∴∠BDC=∠C,∴BD=BC,∴AD=BD=BC,故C正确;
∵BD>CD,∴AD>CD,∴点D不是线段AC的中点,故D错误.
3.如图所示,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下列结论错误的是 ( )
A.BD平分∠ABC
B.△BCD的周长等于AB+BC
C.AD=BD=BC
D.点D是线段AC的中点
D
4.如图所示,已知DE是AC的垂直平分线,AB=
10 cm,BC=11 cm,求△ABD的周长.
解:∵DE垂直平分AC,∴AD=CD,
∴BD+AD=BD+CD=BC=11 cm,
又∵AB=10 cm,
∴△ABD的周长=AB+BC=10+11=21(cm).
八年级数学·上 新课标 [人]
第十三章 轴对称
13.2 线段的垂直平分线的性质(2)
下面的交通标志是轴对称图形吗 如果是轴对称图形,你能找到它的对称轴吗
活动:画对称轴
我们已经学过,如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线,所以我们只要找到两个图形的一对对应点,然后画出以对应点为端点的线段的垂直平分线即可,如何作线段的垂直平分线呢
例2.如图(1)所示,已知点A和点B关于某条直线成轴对称,你能作出这条直线吗
(1)分别以点A,B为圆心,以大于 AB的长为半径作弧(想一想为什么),两弧相交于C,D两点;
(2)作直线CD.
CD就是所求作的直线.
作法(如图所示)
D
C
这个作法实际上就是线段的垂直平分线的尺规作图.
(1)在作法中为什么有CA=CB,DA=DB
(2)可以用这种方法找线段的中点吗 四等分点呢
例(补充).如图所示,△ABC和△A'B'C'是两个成轴对称的图形,请画出它的对称轴.
把问题转化为已解决问题,只要画出点A、点A'连线的垂直平分线即可.
例.图是一个五角星,请画出它的对称轴.
作对称轴的前提是两个图形成轴对称或一个图形是轴对称图形,否则,不存在对称轴。
两个图形成轴对称时,任找一对对应点,作出连接它们的线段的垂直平分线就是对称轴.
对于轴对称图形,由于对称轴可能不是唯一的,因此,要注意选取不同类型的对应点,作出其所有的对称轴.
B
1.正六边形的对称轴有 ( )
A.3条 B.6条 C.9条 D.12条
D
2.如图所示的四角星图形是轴对称图形,它共有对称轴 ( )
A.1条 B.2条 C.3条 D.4条
3.下列图形中,对称轴条数最多的是 ( )
解析:A.如图所示,该图形的对称轴有4条;
B.如图所示,该图形的对称轴有6条;
C.如图所示,该图形的对称轴有3条;
D.如图所示,该图形的对称轴有5条.
综上所述,对称轴条数最多的是B选项.
4.如图所示,作出它们的对称轴.
谢 谢 观 看
