24.1.4 圆周角 提升练习(无答案) 人教版九年级数学上册
文档属性
| 名称 | 24.1.4 圆周角 提升练习(无答案) 人教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 407.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-09 07:30:48 | ||
图片预览

文档简介
24.1.4 圆周角 提升练习
一、选择题
1.如图所示,点A,B,P为上的点,若,且,则等于( )
A. B. C. D.
2.如图,在中,直径与弦相交于点P,连接,若,,则( )
A. B. C. D.
3.如图,在中,弦,圆周角,则的半径等于( )
A. B. C. D.
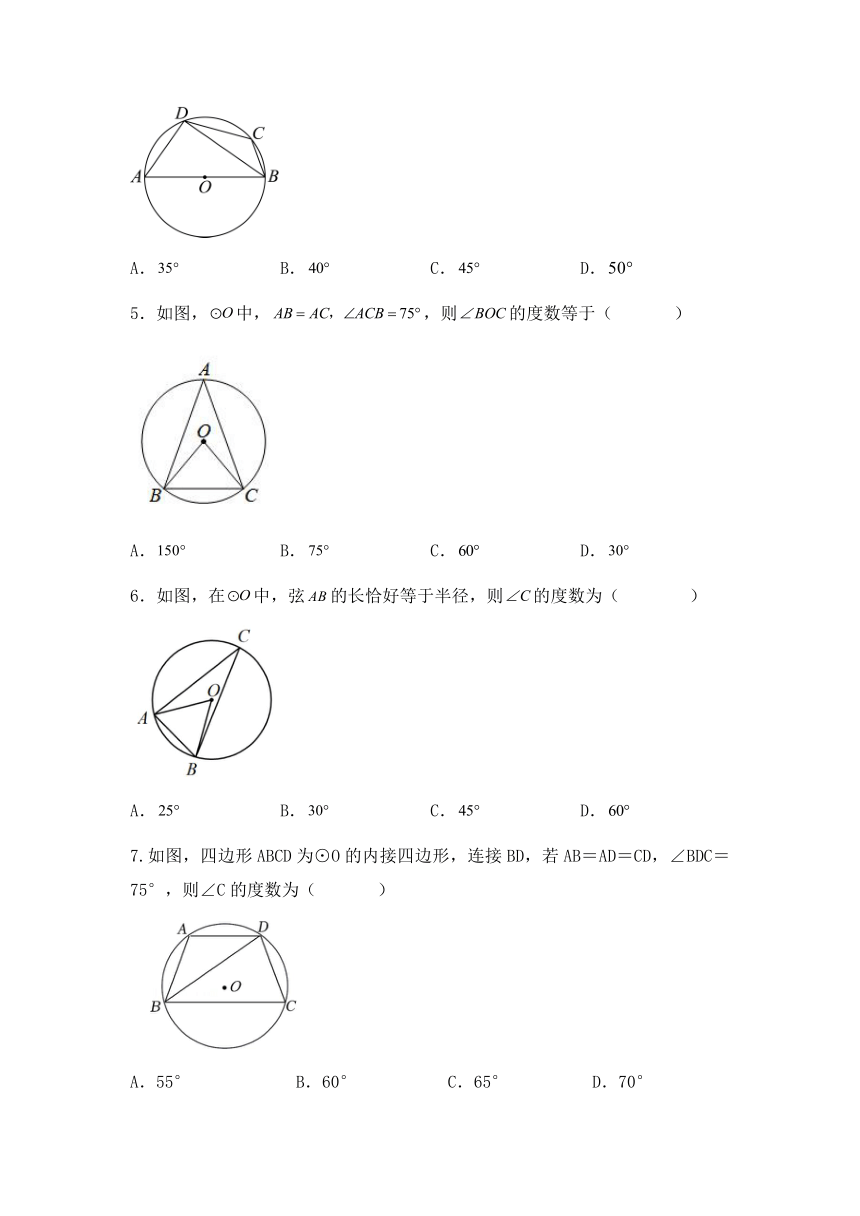
4.如图,四边形内接于是的直径,连接.若,则的度数为( )
A. B. C. D.
5.如图,中,,则的度数等于( )
A. B. C. D.
6.如图,在中,弦的长恰好等于半径,则的度数为( )
A. B. C. D.
7.如图,四边形ABCD为⊙O的内接四边形,连接BD,若AB=AD=CD,∠BDC=75°,则∠C的度数为( )
A.55° B.60° C.65° D.70°
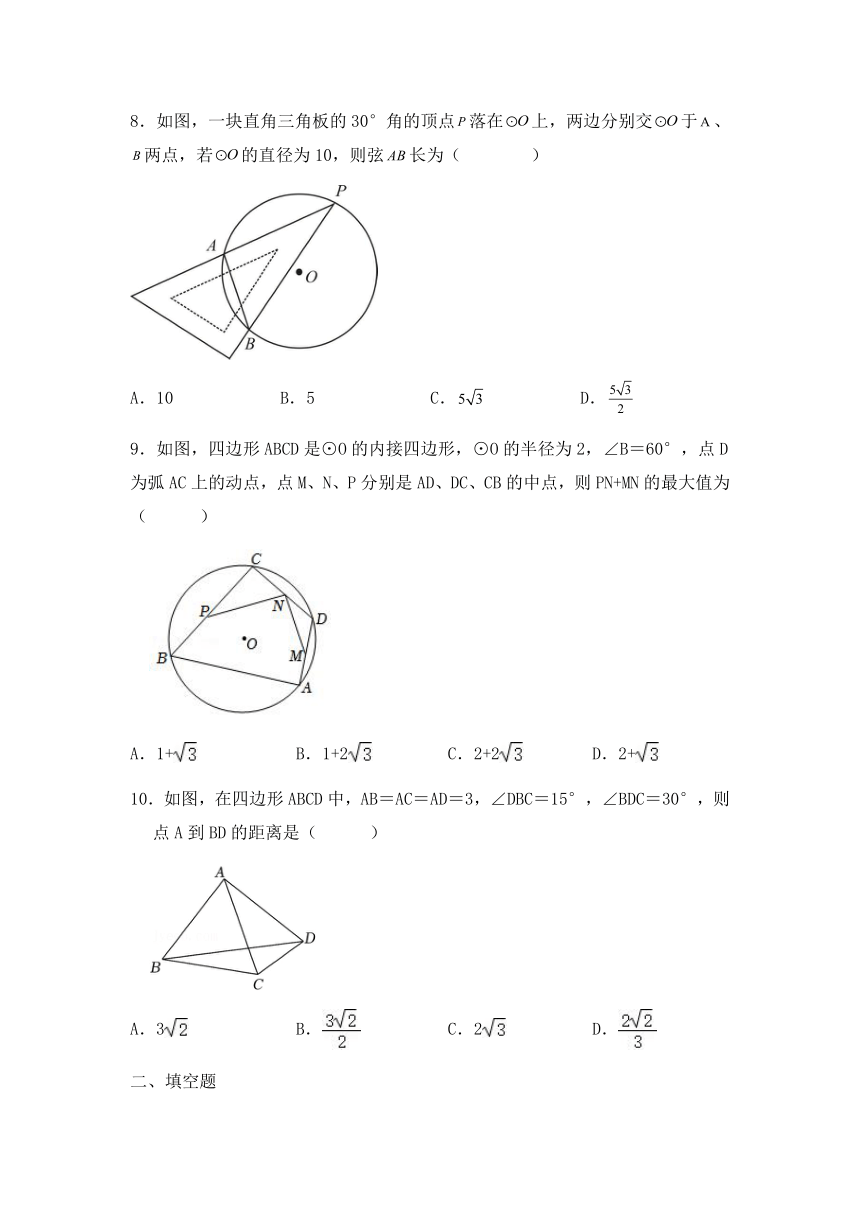
8.如图,一块直角三角板的30°角的顶点落在上,两边分别交于、两点,若的直径为10,则弦长为( )
A.10 B.5 C. D.
9.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=60°,点D为弧AC上的动点,点M、N、P分别是AD、DC、CB的中点,则PN+MN的最大值为( )
A.1+ B.1+2 C.2+2 D.2+
10.如图,在四边形ABCD中,AB=AC=AD=3,∠DBC=15°,∠BDC=30°,则点A到BD的距离是( )
A.3 B. C.2 D.
填空题
1.在圆内接四边形中,, .
2.如图,若△ABC内接于半径为6的⊙O,且∠A=60°,连接OB、OC,则边BC的长为 .
3.如图,是圆O的直径,弦交于点E,连接.若,则 .
4.如图,已知内接于,是的直径,CD平分∠ACB交于点.若,则的长为 .
5.如图,已知四边形ABCD内接于⊙O,AD是直径,∠ABC=120°,CD=3,则弦AC= .
6.如图,是的直径,点C、D是上的点.且,分别与、相交于点E,F.若的半径为5,,点P是线段上任意一点,则的最小值是 .
解答题
1.如图,已知⊿ABC中,AB=AC.∠A=45°. AB为⊙O的直径,AC交⊙O于点E. 连接BE
(1)求∠EBC的度数
(2)求证:BD=CD
2.如图,四边形ABDC内接于⊙O,∠BOC=120°,AD平分∠BAC交⊙O于点D,连接OB,OC,BD,CD.
(1)求证:四边形OBDC是菱形;
(2)若∠ABO=15°,OB=2,求弦AC长.
3.如图,已知EF过圆O的圆心O,且弦AB⊥EF,连接AE交⊙O于点C,连接BC交EF于点D,连接OB、OC.
(1)若∠E=24°,求∠BOC的度数;
(2)若OB=2,OD=1,求DE的长.
4.如图,四边形ABCD内接于⊙O,BD为直径,AC平分∠BCD.
(1)若BC=5cm,CD=12cm,求AB的长;
(2)求证:BC+CD=AC.
5.如图1,C,D是半圆上的两点,若直径上存在一点P,满足,则称是弧的“幸运角”.
(1)如图2,是⊙O的直径,弦,D是弧上的一点,连接交于点P,连接.
①是弧的“幸运角”吗?请说明理由;
②设弧的度数为n,请用含n的式子表示弧的“幸运角”度数;
(2)如图3,在(1)的条件下,若直径,弧的“幸运角”为,,求的长.
一、选择题
1.如图所示,点A,B,P为上的点,若,且,则等于( )
A. B. C. D.
2.如图,在中,直径与弦相交于点P,连接,若,,则( )
A. B. C. D.
3.如图,在中,弦,圆周角,则的半径等于( )
A. B. C. D.
4.如图,四边形内接于是的直径,连接.若,则的度数为( )
A. B. C. D.
5.如图,中,,则的度数等于( )
A. B. C. D.
6.如图,在中,弦的长恰好等于半径,则的度数为( )
A. B. C. D.
7.如图,四边形ABCD为⊙O的内接四边形,连接BD,若AB=AD=CD,∠BDC=75°,则∠C的度数为( )
A.55° B.60° C.65° D.70°
8.如图,一块直角三角板的30°角的顶点落在上,两边分别交于、两点,若的直径为10,则弦长为( )
A.10 B.5 C. D.
9.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=60°,点D为弧AC上的动点,点M、N、P分别是AD、DC、CB的中点,则PN+MN的最大值为( )
A.1+ B.1+2 C.2+2 D.2+
10.如图,在四边形ABCD中,AB=AC=AD=3,∠DBC=15°,∠BDC=30°,则点A到BD的距离是( )
A.3 B. C.2 D.
填空题
1.在圆内接四边形中,, .
2.如图,若△ABC内接于半径为6的⊙O,且∠A=60°,连接OB、OC,则边BC的长为 .
3.如图,是圆O的直径,弦交于点E,连接.若,则 .
4.如图,已知内接于,是的直径,CD平分∠ACB交于点.若,则的长为 .
5.如图,已知四边形ABCD内接于⊙O,AD是直径,∠ABC=120°,CD=3,则弦AC= .
6.如图,是的直径,点C、D是上的点.且,分别与、相交于点E,F.若的半径为5,,点P是线段上任意一点,则的最小值是 .
解答题
1.如图,已知⊿ABC中,AB=AC.∠A=45°. AB为⊙O的直径,AC交⊙O于点E. 连接BE
(1)求∠EBC的度数
(2)求证:BD=CD
2.如图,四边形ABDC内接于⊙O,∠BOC=120°,AD平分∠BAC交⊙O于点D,连接OB,OC,BD,CD.
(1)求证:四边形OBDC是菱形;
(2)若∠ABO=15°,OB=2,求弦AC长.
3.如图,已知EF过圆O的圆心O,且弦AB⊥EF,连接AE交⊙O于点C,连接BC交EF于点D,连接OB、OC.
(1)若∠E=24°,求∠BOC的度数;
(2)若OB=2,OD=1,求DE的长.
4.如图,四边形ABCD内接于⊙O,BD为直径,AC平分∠BCD.
(1)若BC=5cm,CD=12cm,求AB的长;
(2)求证:BC+CD=AC.
5.如图1,C,D是半圆上的两点,若直径上存在一点P,满足,则称是弧的“幸运角”.
(1)如图2,是⊙O的直径,弦,D是弧上的一点,连接交于点P,连接.
①是弧的“幸运角”吗?请说明理由;
②设弧的度数为n,请用含n的式子表示弧的“幸运角”度数;
(2)如图3,在(1)的条件下,若直径,弧的“幸运角”为,,求的长.
同课章节目录
