数学必修3统计部分单元复习 上学期
文档属性
| 名称 | 数学必修3统计部分单元复习 上学期 |

|
|
| 格式 | rar | ||
| 文件大小 | 252.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-22 00:00:00 | ||
图片预览







文档简介
课件21张PPT。第二章 统 计
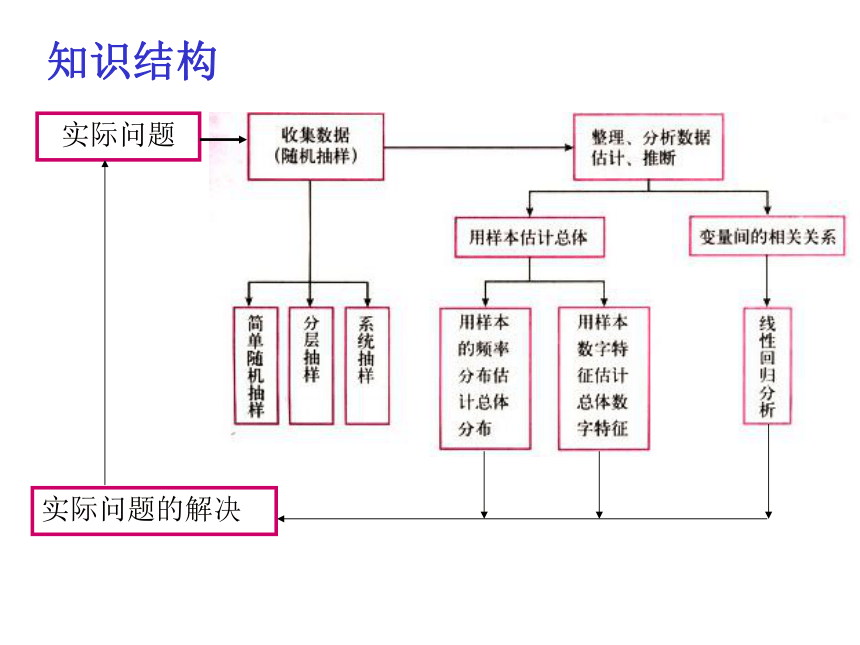
复 习知识结构1.简单随机抽样 设一个总体的个数为N,如果通过逐个抽取的方法从中抽取一个样本,且每次抽取时各个个体被抽到的概率相等,就称这样的抽样为简单随机抽样。 如果用简单随机抽样从个体数为N的总体中抽取一个容量为n的样本,那么每个个体被抽到的概率都等于(1)要求被抽取样本的总体的个体数有限;
(2)它是不放回抽样;
(3)它是逐个进行抽取;
(4)它是一种等概率抽样。 (一)定义:(二)个体入样的概率:(三)简单随机抽样的特点:2.1 随机抽样 1.简单随机抽样(一)抽签法 3.优点:简单易行。 2.适用范围:总体的个体数不多时1.步骤:一是标号;
二是做号签,放回均匀搅拌;
三是逐个抽取。(二)随机数表法第一步 编号(位数相同);
第二步 在随机数表中选定开始数与方向
第三步 获取样本的号码,抽足为止(去掉其中不合要求和与前面重复的数)2.系统抽样 当总体的个体比较多时,将总体分成均衡的几个部分,然后按照预先定出的规则,从每一个部分抽取一个个体,得到所需要的样本,这样的抽样叫做系统抽样。
第一步:编号(在保证编号的随机性的前提下,可以直接利用个体所带有的号码)
第二步:分段(定分段间隔习惯于
,注意剔除部分个体时,要保证随机性和客观性)
第三步:确定起始个体号 (在第一段采用简单随机抽样来确定)
第四步:按照事先确定的规则抽取样本(通常逐个加k.即所得样本的编号分别为(1)概念:(2)系统抽样的步骤分层抽样步骤:
第一步求出样本容量与总体的个体数之比n:N,
第二步各层数量乘比值n:N,得各层应抽数(需为整数时可进行四舍五入),
第三步采用简单随机抽样(抽签或随机数表法)或系统抽样的方法从各个层中分别抽取,然后合在一起,就是所抽取的样本。 分层抽样定义:当已知总体由差异明显的几部分组成时,为了使样本更充分地反映总体的情况,常将总体分成几部分,然后按照各部分所占的比进行抽样,这种抽取叫做分层抽样,其中所分成的各部分叫做层。 3.分层抽样1、求极差(即一组数据中最大值与最小值的差)
知道这组数据的变动范围2、决定组距与组数(组数取整)3、 将数据分组1.画频率分布直方图的步骤4、列出频率分布表.(填写频率/组距一栏)5、画出频率分布直方图(高度=频率/组距)。组距:指每个小组的两个端点的距离
组数:将数据分组,当数据在100个以内时,
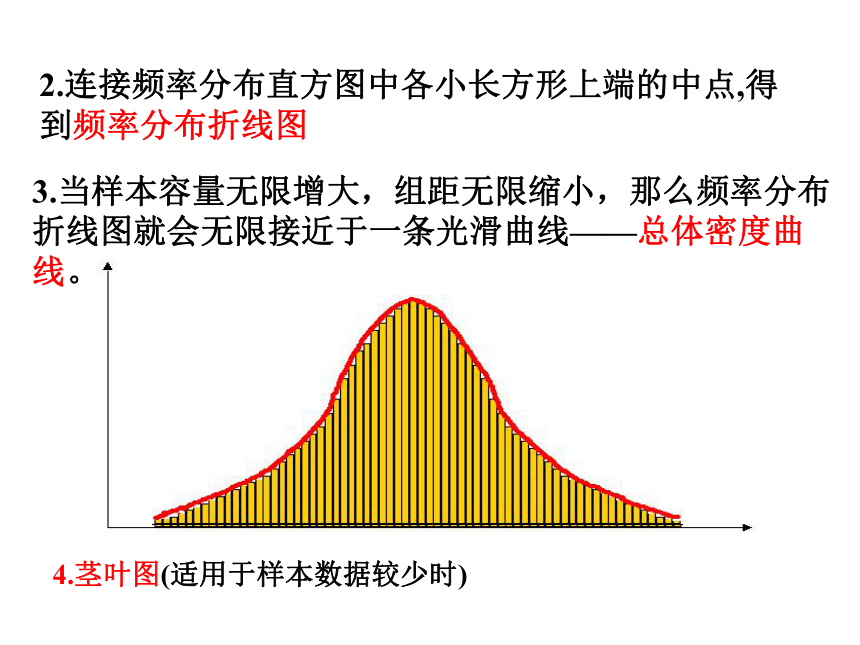
按数据多少常分5-12组。2.2 用样本估计总体2.2.1用样本的频率分布估计总体分布说明:小长方形面积=频率,所有小正方形面积=12.连接频率分布直方图中各小长方形上端的中点,得到频率分布折线图3.当样本容量无限增大,组距无限缩小,那么频率分布折线图就会无限接近于一条光滑曲线——总体密度曲线。4.茎叶图(适用于样本数据较少时)2.2.2 用样本的数字特征估计总体的数字特征1、众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标。2.在频率分布直方图中,中位数左边和右边的直方图的面积应该相等,由此可以估计中位数的值。3.平均数在频率分布直方图中是每个小矩形的面积乘以小矩形底边中点的横坐标之和.(一)众数、中位数、平均数4.三种数字特征的优缺点众数体现了样本数据的最大集中点,但它对其它数据信息的忽视使得无法客观地反映总体特征中位数是样本数据所占频率的等分线,它不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值的不敏感有时也会成为缺点。平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变,可以反映出更多的关于样本数据全体的信息,但平均数受数据中的极端值的影响较大,使平均数在估计时可靠性降低。 (二).标准差标准差考察样本数据的分散程度的大小计算标准差公式方差:标准差的平方标准差越大,样本数据越分散
标准差越小,样本数据越集中1.相关关系:自变量取值一定时,因变量的取值带有一定的随机性的两个变量之间的关系叫做相关关系。它是一种非确定性关系。 2.3 变量间的相互关系2.线性相关关系:如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系.这条直线叫做回归直线,该直线方程叫回归方程直线过定点4.相关系数 可以证明, ,且 越接近于1,相关程度越大; 越接近于0,相关程度越小.
r在[-1,-0.75],负相关很强;
r在[0.75,1], 正相关很强;
r在[-0.75,-0.30]或[0.30,0.75],相关性一般
r在[-0.25,0.25],相关较弱;1.学校共有师生2400人,现用分层抽样的方法,从所有师生中抽取一个容量为160的样本,已知从学生中抽取的人数为150,那么该学校的教师人数是 .150人综合应用2.有A、B、C三种零件,分别为a个,300个,200个.采用分层抽样法抽取一个容量为45的样本,A种零件被抽取20个,C种零件被抽取10个,则这三种零件共有 个.900综合应用2,23,20,5 4.一个总体的80个个体编号为0,1,2,…,79,并依次将其分成8个小组,组号为0, 1,2,…,7,要用系统抽样的方法抽取一个容量为8的样本,即规定先在第0组随机抽取一个号码,记为m,依次错位地得到后面各组的号码,即第k组中抽取的号码的
个位数为m+k或m+k-10(若m+k≥10).则在m=6时,所抽到的8个号码是____________________. 综合应用6,17,28,39,40,51,62,73.5.已知一组数据x1,x2,x3,x4,x5,它们的平均数为20,如果把x1改写成40,那么新数据40, x2,x3,x4,x5,的平均值为25,则原先的x1等于是 .15综合应用6.已知两组数据x1,x2,…,xn,与y1,y2,…,yn,它们的平均数分别为 ,标准差分别是s1,s2,则新的一组数据2x1-3y1+1, 2x2-3y2+1, …,2xn-3yn+1,的平均数是 , 3y1+1, 3y2+1, …, 3yn+1方差是 .9s227.(07广东)下表提供了某厂节能降耗技术发行后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y=(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)y=0.7x+0.3519.658.为考虑广告费用x与销售额y之间的关系,抽取了5家餐厅,得到如相数据:现要使销售额达到6万元,则需广告费用为 。(保留两位有效数学)综合应用9.有一个样本容量为100的数据分组,各组的频数如下: (17,19],1;(19,21],1;(21,23],3;(23,25],3;(25,27],18;(27,29],16;(29,31],28;(31,33],30;
(1)画出频率分布直方图
(2)估计小于29的数据的频率
(3)求出样本的众数、中位数、平均数、方差综合应用 10、一个总体中的100个个体编号为0,1,2,…,99,并依次将其分为10个小组,组号为0,1,2,…,9,要用系统抽样方法抽取一个容量为10的样本,规定如果在第0组(号码0~9)随机抽取的号码为l(0≤l≤9),那么第k组抽取的号码为个位数等于l+pk除以10的余数,这时p是一个和10互素的整数,如果l=p=7,所抽取的10个号码依次是什么?11、求三点(3,10),(7,20),(11,24)的回归直线,直线经过哪个定点?所求直线经过以上三点的哪点?
复 习知识结构1.简单随机抽样 设一个总体的个数为N,如果通过逐个抽取的方法从中抽取一个样本,且每次抽取时各个个体被抽到的概率相等,就称这样的抽样为简单随机抽样。 如果用简单随机抽样从个体数为N的总体中抽取一个容量为n的样本,那么每个个体被抽到的概率都等于(1)要求被抽取样本的总体的个体数有限;
(2)它是不放回抽样;
(3)它是逐个进行抽取;
(4)它是一种等概率抽样。 (一)定义:(二)个体入样的概率:(三)简单随机抽样的特点:2.1 随机抽样 1.简单随机抽样(一)抽签法 3.优点:简单易行。 2.适用范围:总体的个体数不多时1.步骤:一是标号;
二是做号签,放回均匀搅拌;
三是逐个抽取。(二)随机数表法第一步 编号(位数相同);
第二步 在随机数表中选定开始数与方向
第三步 获取样本的号码,抽足为止(去掉其中不合要求和与前面重复的数)2.系统抽样 当总体的个体比较多时,将总体分成均衡的几个部分,然后按照预先定出的规则,从每一个部分抽取一个个体,得到所需要的样本,这样的抽样叫做系统抽样。
第一步:编号(在保证编号的随机性的前提下,可以直接利用个体所带有的号码)
第二步:分段(定分段间隔习惯于
,注意剔除部分个体时,要保证随机性和客观性)
第三步:确定起始个体号 (在第一段采用简单随机抽样来确定)
第四步:按照事先确定的规则抽取样本(通常逐个加k.即所得样本的编号分别为(1)概念:(2)系统抽样的步骤分层抽样步骤:
第一步求出样本容量与总体的个体数之比n:N,
第二步各层数量乘比值n:N,得各层应抽数(需为整数时可进行四舍五入),
第三步采用简单随机抽样(抽签或随机数表法)或系统抽样的方法从各个层中分别抽取,然后合在一起,就是所抽取的样本。 分层抽样定义:当已知总体由差异明显的几部分组成时,为了使样本更充分地反映总体的情况,常将总体分成几部分,然后按照各部分所占的比进行抽样,这种抽取叫做分层抽样,其中所分成的各部分叫做层。 3.分层抽样1、求极差(即一组数据中最大值与最小值的差)
知道这组数据的变动范围2、决定组距与组数(组数取整)3、 将数据分组1.画频率分布直方图的步骤4、列出频率分布表.(填写频率/组距一栏)5、画出频率分布直方图(高度=频率/组距)。组距:指每个小组的两个端点的距离
组数:将数据分组,当数据在100个以内时,
按数据多少常分5-12组。2.2 用样本估计总体2.2.1用样本的频率分布估计总体分布说明:小长方形面积=频率,所有小正方形面积=12.连接频率分布直方图中各小长方形上端的中点,得到频率分布折线图3.当样本容量无限增大,组距无限缩小,那么频率分布折线图就会无限接近于一条光滑曲线——总体密度曲线。4.茎叶图(适用于样本数据较少时)2.2.2 用样本的数字特征估计总体的数字特征1、众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标。2.在频率分布直方图中,中位数左边和右边的直方图的面积应该相等,由此可以估计中位数的值。3.平均数在频率分布直方图中是每个小矩形的面积乘以小矩形底边中点的横坐标之和.(一)众数、中位数、平均数4.三种数字特征的优缺点众数体现了样本数据的最大集中点,但它对其它数据信息的忽视使得无法客观地反映总体特征中位数是样本数据所占频率的等分线,它不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值的不敏感有时也会成为缺点。平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变,可以反映出更多的关于样本数据全体的信息,但平均数受数据中的极端值的影响较大,使平均数在估计时可靠性降低。 (二).标准差标准差考察样本数据的分散程度的大小计算标准差公式方差:标准差的平方标准差越大,样本数据越分散
标准差越小,样本数据越集中1.相关关系:自变量取值一定时,因变量的取值带有一定的随机性的两个变量之间的关系叫做相关关系。它是一种非确定性关系。 2.3 变量间的相互关系2.线性相关关系:如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系.这条直线叫做回归直线,该直线方程叫回归方程直线过定点4.相关系数 可以证明, ,且 越接近于1,相关程度越大; 越接近于0,相关程度越小.
r在[-1,-0.75],负相关很强;
r在[0.75,1], 正相关很强;
r在[-0.75,-0.30]或[0.30,0.75],相关性一般
r在[-0.25,0.25],相关较弱;1.学校共有师生2400人,现用分层抽样的方法,从所有师生中抽取一个容量为160的样本,已知从学生中抽取的人数为150,那么该学校的教师人数是 .150人综合应用2.有A、B、C三种零件,分别为a个,300个,200个.采用分层抽样法抽取一个容量为45的样本,A种零件被抽取20个,C种零件被抽取10个,则这三种零件共有 个.900综合应用2,23,20,5 4.一个总体的80个个体编号为0,1,2,…,79,并依次将其分成8个小组,组号为0, 1,2,…,7,要用系统抽样的方法抽取一个容量为8的样本,即规定先在第0组随机抽取一个号码,记为m,依次错位地得到后面各组的号码,即第k组中抽取的号码的
个位数为m+k或m+k-10(若m+k≥10).则在m=6时,所抽到的8个号码是____________________. 综合应用6,17,28,39,40,51,62,73.5.已知一组数据x1,x2,x3,x4,x5,它们的平均数为20,如果把x1改写成40,那么新数据40, x2,x3,x4,x5,的平均值为25,则原先的x1等于是 .15综合应用6.已知两组数据x1,x2,…,xn,与y1,y2,…,yn,它们的平均数分别为 ,标准差分别是s1,s2,则新的一组数据2x1-3y1+1, 2x2-3y2+1, …,2xn-3yn+1,的平均数是 , 3y1+1, 3y2+1, …, 3yn+1方差是 .9s227.(07广东)下表提供了某厂节能降耗技术发行后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y=(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)y=0.7x+0.3519.658.为考虑广告费用x与销售额y之间的关系,抽取了5家餐厅,得到如相数据:现要使销售额达到6万元,则需广告费用为 。(保留两位有效数学)综合应用9.有一个样本容量为100的数据分组,各组的频数如下: (17,19],1;(19,21],1;(21,23],3;(23,25],3;(25,27],18;(27,29],16;(29,31],28;(31,33],30;
(1)画出频率分布直方图
(2)估计小于29的数据的频率
(3)求出样本的众数、中位数、平均数、方差综合应用 10、一个总体中的100个个体编号为0,1,2,…,99,并依次将其分为10个小组,组号为0,1,2,…,9,要用系统抽样方法抽取一个容量为10的样本,规定如果在第0组(号码0~9)随机抽取的号码为l(0≤l≤9),那么第k组抽取的号码为个位数等于l+pk除以10的余数,这时p是一个和10互素的整数,如果l=p=7,所抽取的10个号码依次是什么?11、求三点(3,10),(7,20),(11,24)的回归直线,直线经过哪个定点?所求直线经过以上三点的哪点?
