平方差公式

平 方 差 公 式
教材分析
《平方差公式》是义务教育课程标准实验教科书《数学》（北师大版）七年级下册的教学内容。教材在上册中安排了《有理数及运算》、《字母表示数》等内容。在本节内容前面又安排了平方差公式产生的背景，使学生经历过实际问题“符号化”的过程，有了一定的符号感，为探索“平方差公式”奠定了基础。
学生分析
学生在前面的学习中，已经学习了整式的有关内容，并经历了用字母表示数量关系的过程，有了一定的符号感。经过一个学期的培养，学生已经具备了小组合作、交流的能力。本节课的教学能培养学生的推理能力，使学生通过大胆而又合情合理的推理，有条理地表达自己的思考过程。
教学目标
1、经历探索平方差公式的过程，进一步发展符号感和推理能力。
2、会推导平方差公式，并能运用公式进行简单的计算。
3、认识平方差公式及其几何背景。
4、在合作、交流和讨论中发掘知识，并体验学习的乐趣。
教学重点：体会公式的发现的推导过程，理解公式的本质，并会运用公式进行简单的计算。
教学难点：从广泛意义上理解公式中的字母含义。
课前准备
1、为每位学生准备一张正方形纸片(边长为15cm)。
2、教师准备两张正方形(一大一小)纸板和三块矩形纸板。
3、多媒体课件。
教学流程
1、 创设问题情境，引导学生观察、设想。
教师发给每个学生一张正方形纸片(边长15cm)并用多媒体课件(或用正方形纸板)显示正方形。
师：在一块45的红色正方形纸板上，因为工作的需要，中间挖去一块边长为15的正方形(如图)，请问剩下红色部分的面积有多少平方厘米？
45
30
15
(刚开始小的正方形可以随意摆放在红色正方形的任何位置。)
小组讨论：
1． 可以用大正方形面积减去小正方形面积得到。
2． 可以把剩下红色部分切割成几个矩形来计算。
师：从今天的问题来看，用哪一种方法比较好？你们小组能列出算式吗？
或许有学生能迅速列出算式，得出答案是1800平方厘米。
师：为了容易理解，我现在把小正方形放在大正方形的角落(如图)。
(同时也要求学生在他们手上的正方形纸的角落上画一个小正方形，可规定连长为3cm。)
45
30
15
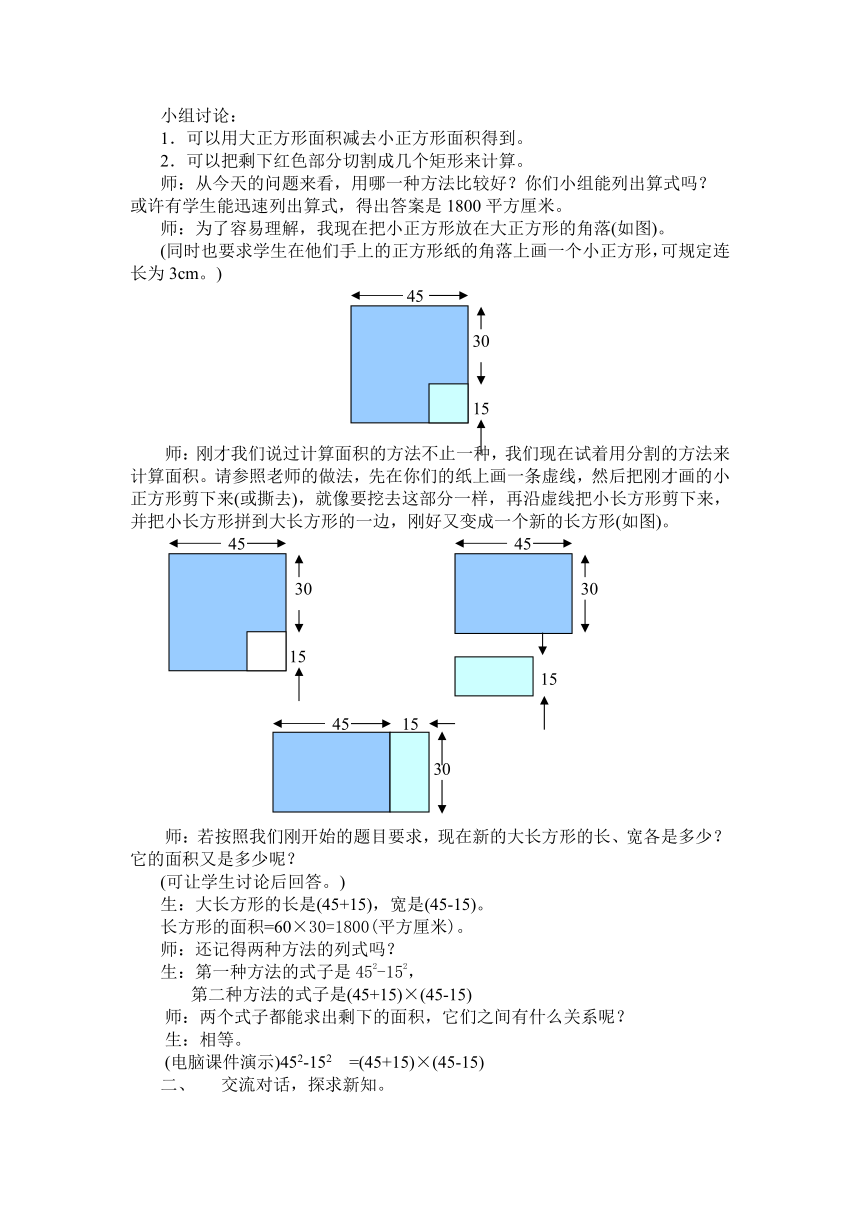
师：刚才我们说过计算面积的方法不止一种，我们现在试着用分割的方法来计算面积。请参照老师的做法，先在你们的纸上画一条虚线，然后把刚才画的小正方形剪下来(或撕去)，就像要挖去这部分一样，再沿虚线把小长方形剪下来，并把小长方形拼到大长方形的一边，刚好又变成一个新的长方形(如图)。
45 45
30 30
15
15
45 15
30
师：若按照我们刚开始的题目要求，现在新的大长方形的长、宽各是多少？它的面积又是多少呢？
(可让学生讨论后回答。)
生：大长方形的长是(45+15)，宽是(45-15)。
长方形的面积=60×30=1800(平方厘米)。
师：还记得两种方法的列式吗？
生：第一种方法的式子是452-152，
第二种方法的式子是(45+15)×(45-15)
师：两个式子都能求出剩下的面积，它们之间有什么关系呢？
生：相等。
(电脑课件演示)452-152 =(45+15)×(45-15)
2、 交流对话，探求新知。
看谁算得快：
(1) (x+2)(x-2)
(2) (1+3a)(1-3a)
(3) (x+5y)(x-5y)
(4) (-m+n)(-m-n)
师：你们能发现什么规律？
(学生议论、讨论，各抒己见。)
师：再想想看，如果今天的题目换成：“在一块边长为厘米的正方形纸板上，因为工作的需要，中间挖去为b厘米的小正方形，请问剩下的面积有多少？”我们该怎样列代数式来表示？
生：我们可以用a2-b2来表示剩下的面积。
师：还有没有别的方法？
生：也可以用(a+b)(a-b)来表示剩下的面积。
师：今天我们除了找一个比较方便的方法来求面积外，更重要的是我们能从图形中了解到(a+b)(a-b)=a2-b2这个性质。上一节课我们已经学过多项式的乘法，你能利用计算多项式乘法的方法，把(a+b)(a-b)的答案计算出来吗？
(找学生在黑板上把过程写出来。)
师：为了节省计算时间，我们把(a+b)(a-b)=a2-b2作为公式来运用，把这个公式称为“平方差公式”。
（电脑演示）平方差公式：(a+b)(a-b)=a2-b2
师：哪一位同学能用语言叙述一下平方差公式？
生：两数和与这两数差的积，等于它们的平方差。
3、 运用新知，体验成功。
1、例题。
利用平方差公式计算：
(1) (5+6x)(5-6x)
(2) (3m-2n)(3m+2n)
(3) (-4x+1)(-4x-1)
(4) (- 1/4 x - y)( - 1/4 x + y)
(5) (ab+8)(ab-8)
(6) (m+n)(m-n)+3n2
解：(1) 原式＝52-(6x)2=25-36x2
(2) 原式＝(3m)2-(2n)2=9m2-4n2
(3) 原式＝(-4x)2-12=16x2-1
(4) 原式＝(- 1/4 x)2-y2=1/16 x2-y2
(5) 原式＝(ab)2-82=a2b2-64
(6) 原式＝m2-n2+3n2=m2+2n2
2、巩固深化，拓展思维。
利用平方差公式计算：
(1) (a+2)(a-2)
(2) (3a+2b)( 3a-2b)
(3) (-x+1)( -x-1)
(4) (-4k+3)( -4k-3)
(5) (a+b+c)(a+b-c)
四、课堂小结。
1、通过本节课的学习活动，你们认识了什么？
2、什么样的式子才能使用平方差公式？
五、课外作业
1、 基础训练（略）。
2、 拓展训练：利用平方差公式计算(a+b+c)(a+b-c)。