三角形全等的判定复习课(广东省中山市)
文档属性
| 名称 | 三角形全等的判定复习课(广东省中山市) |

|
|
| 格式 | rar | ||
| 文件大小 | 513.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-24 00:00:00 | ||
图片预览





文档简介
课件42张PPT。全等三角形复习全等三角形(复习)知识结构全等三角形定义:能够 的 个三角形对应元素:对应顶点、对应 、对应 。性质:全等三角形的对应边 、 。判定: 、 、 、 、 。完全重合两边角相等对应角相等SSSSASASAAAS HL两个三角形全等的判定方法
1、边边边公理:三条边对应相等的两个三角形全等。(SSS)
2、边角边公理:有两边及其夹角对应相等的两个三角形全等。 (SAS)
3、角边角公理:有两角及其夹边对应相等的两个三角形全等。 (ASA)
4、角角边定理:有两角及一角的对边对应相等的两个三角形全等。 (AAS)
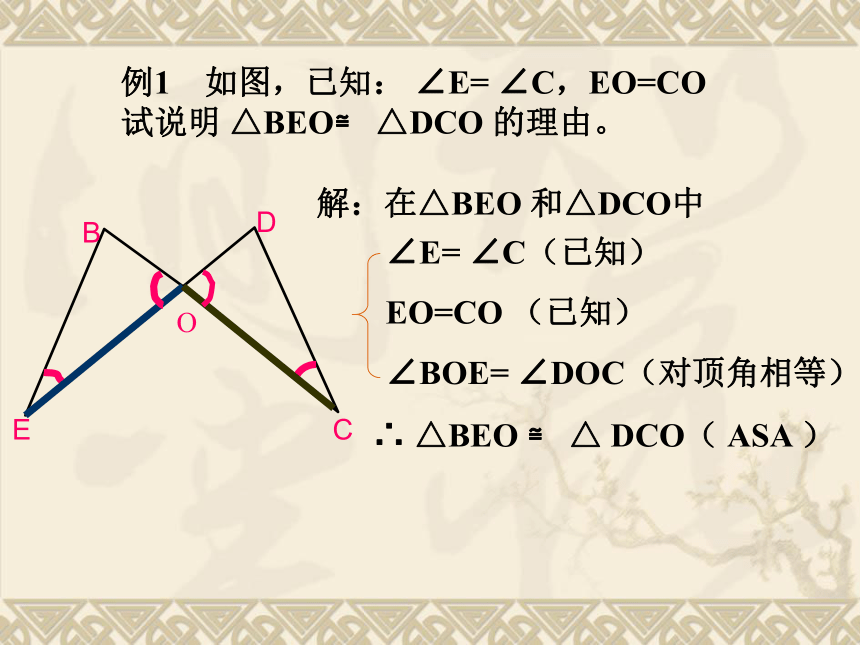
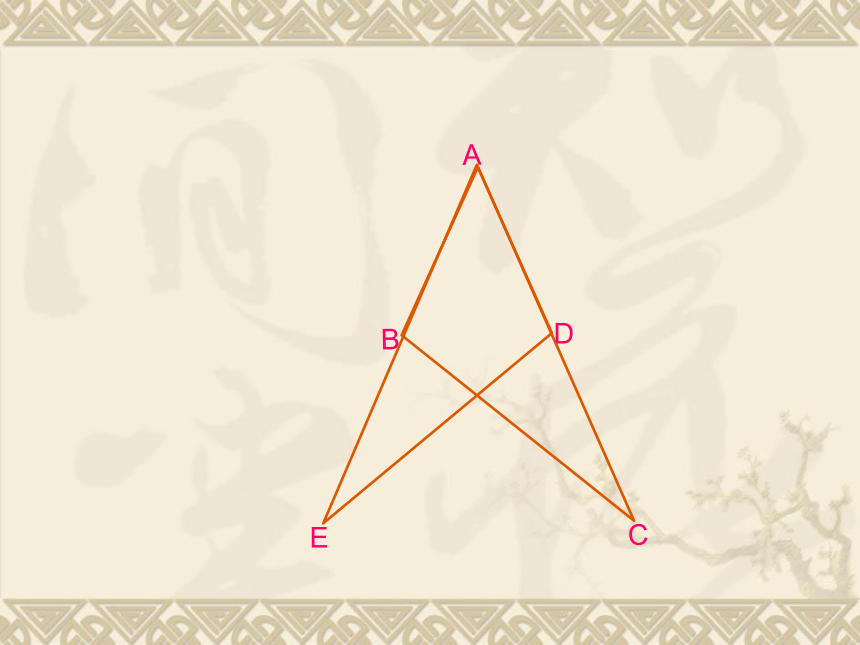
例1 如图,已知: ∠E= ∠C,EO=CO
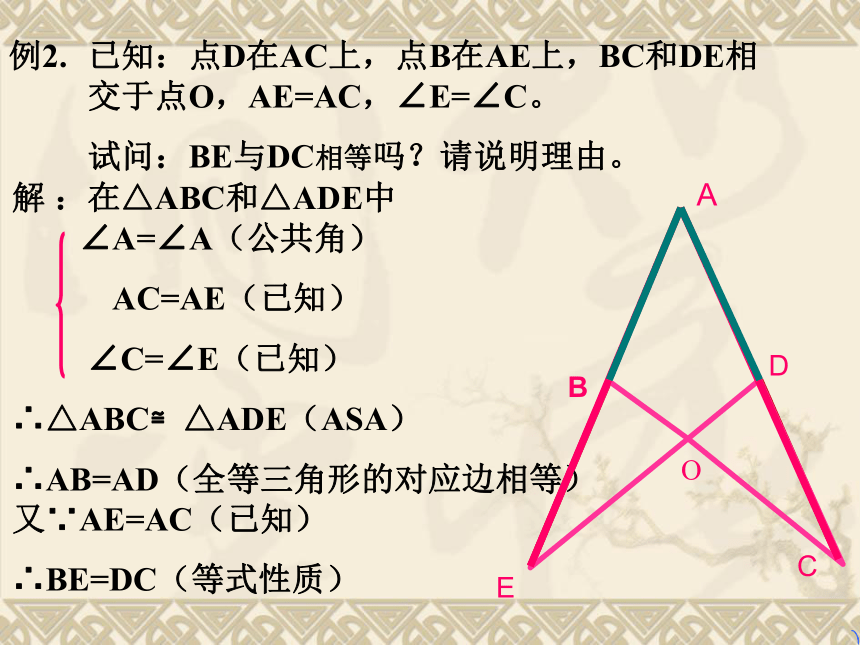
试说明 △BEO≌ △DCO 的理由。BEDCA解 :在△ABC和△ADE中
∠A=∠A(公共角)
AC=AE(已知)
∠C=∠E(已知)
∴△ABC≌△ADE(ASA)
∴AB=AD(全等三角形的对应边相等)
又∵AE=AC(已知)
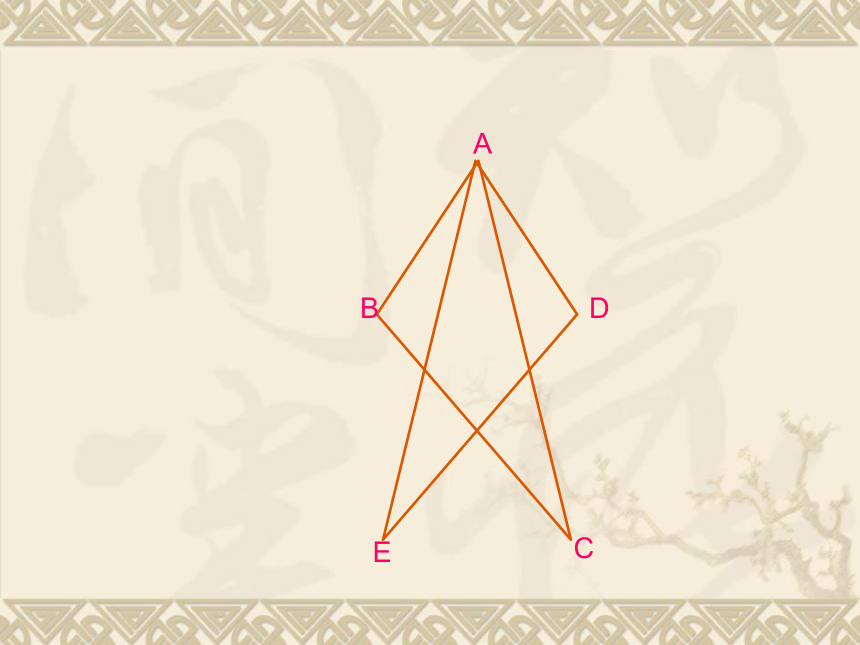
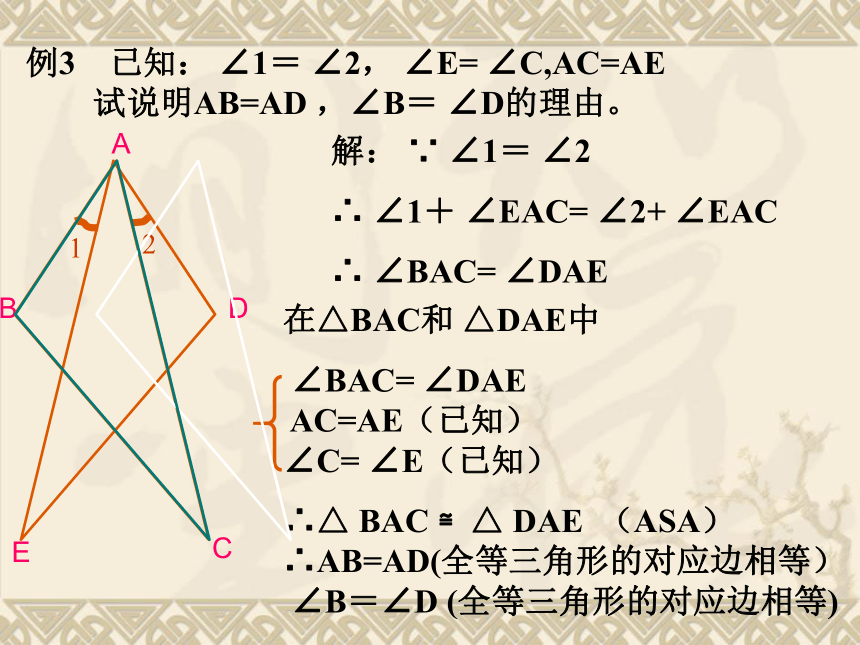
∴BE=DC(等式性质)O12例3 已知: ∠1= ∠2, ∠E= ∠C,AC=AE
试说明AB=AD ,∠B= ∠D的理由。解: ∵ ∠1= ∠2
∴ ∠1+ ∠EAC= ∠2+ ∠EAC
∴ ∠BAC= ∠DAE在△BAC和 △DAE中
∠BAC= ∠DAE
AC=AE(已知)
∠C= ∠E(已知)
∴△ BAC ≌△ DAE (ASA)
∴AB=AD(全等三角形的对应边相等)
∠B=∠D (全等三角形的对应边相等)BADCE已知: ∠1= ∠2,∠E= ∠C,AC=AE,D、A、B在一条直线上;试说明点A的位置,并说明理由。12例5 已知,如图,∠1=∠2,∠C=∠D
试说明AC=AD的理由。1、已知:AE=AC,
要想△ABC≌△ADE,应添加什么条件?2、已知:AB=AD,BC=DE;
要想 △ABC≌△ADE,应添加什么条件?3、已知:∠B=∠D,∠C=∠E;
要想△ABC≌△ADE,应添加什么条件?C ′ACBDA’B’D’例6 已知:△ABC≌△A’B’C’,AD、A’D’分别是△ABC, △A’B’C’的高;试说明 AD=A’D’的理由。 例7 已知:如图,已知∠1=∠2,∠3=∠4,BD=CE;试说明AB=AC的理由。CBDEA例8、已知:BD⊥AC,CE⊥AB,∠1=∠2
试说明BE=CD的理由。二.课堂练习(一)1.边角边公理(SAS):∵AB=A′B′∠B=∠B′(BC=B′C′)∴△ABC≌△A’B’C′2、角边角公理(ASA):∵∠B=∠B′( BC=B′C′ )∠C=∠C′∴△ABC≌△A′B’C′.1、如图,已知△ABC≌△ABD,BC和BD是对应边,那么AC= ,∠C= 。
2、如图,△ABC≌△ADE,∠BAC=100°,
∠C=35°,那么∠EAD= ,∠E= 。DABC二.课堂练习(二)AD∠D∠CAB∠C3、△ABC和△A′B′C′的边角条件如图所示,那么这两个三角形( )A、全等;B、不全等;C、不一定全等;D、无法判定4、如图,已知BE=CF且, ∠B=∠DEF, ∠A=∠D,那么△ABC和△DEF是( )
A、全等;B、不全等;C、无法判定。CA基本题型如图:在△ABC中,AD为角平分线,DE⊥AB于E, DF⊥AC于F, AB=10cm,AC=8cm,△ABC的面积是45平方厘米,求DE的长。ABCDEF已知:AE=DF,AE//DF,CE=BF,
AB=10cm,求CD的长。已知:CD⊥AB,BE⊥AC,D、E是垂足BE、CD相交与O。
(1)当∠1=∠2时,求证:OB=OC;
(2)当0B=0C时,求证:∠1=∠2已知:AB//CD,AB=CD,求证:AE=CF二.课堂练习(三)
测量如图河的宽度,某人在河的对岸找到一参照物树木A,视线 AB与河岸垂直,然后该人沿河岸步行10步(每步约0.75M)到O处,进行标记,再向前步行10步到D处,最后背对河岸向前步行20步,此时树木A,标记O,恰好在同一视线上,则河的宽度为 米。15ABODC
1、边边边公理:三条边对应相等的两个三角形全等。(SSS)
2、边角边公理:有两边及其夹角对应相等的两个三角形全等。 (SAS)
3、角边角公理:有两角及其夹边对应相等的两个三角形全等。 (ASA)
4、角角边定理:有两角及一角的对边对应相等的两个三角形全等。 (AAS)
例1 如图,已知: ∠E= ∠C,EO=CO
试说明 △BEO≌ △DCO 的理由。BEDCA解 :在△ABC和△ADE中
∠A=∠A(公共角)
AC=AE(已知)
∠C=∠E(已知)
∴△ABC≌△ADE(ASA)
∴AB=AD(全等三角形的对应边相等)
又∵AE=AC(已知)
∴BE=DC(等式性质)O12例3 已知: ∠1= ∠2, ∠E= ∠C,AC=AE
试说明AB=AD ,∠B= ∠D的理由。解: ∵ ∠1= ∠2
∴ ∠1+ ∠EAC= ∠2+ ∠EAC
∴ ∠BAC= ∠DAE在△BAC和 △DAE中
∠BAC= ∠DAE
AC=AE(已知)
∠C= ∠E(已知)
∴△ BAC ≌△ DAE (ASA)
∴AB=AD(全等三角形的对应边相等)
∠B=∠D (全等三角形的对应边相等)BADCE已知: ∠1= ∠2,∠E= ∠C,AC=AE,D、A、B在一条直线上;试说明点A的位置,并说明理由。12例5 已知,如图,∠1=∠2,∠C=∠D
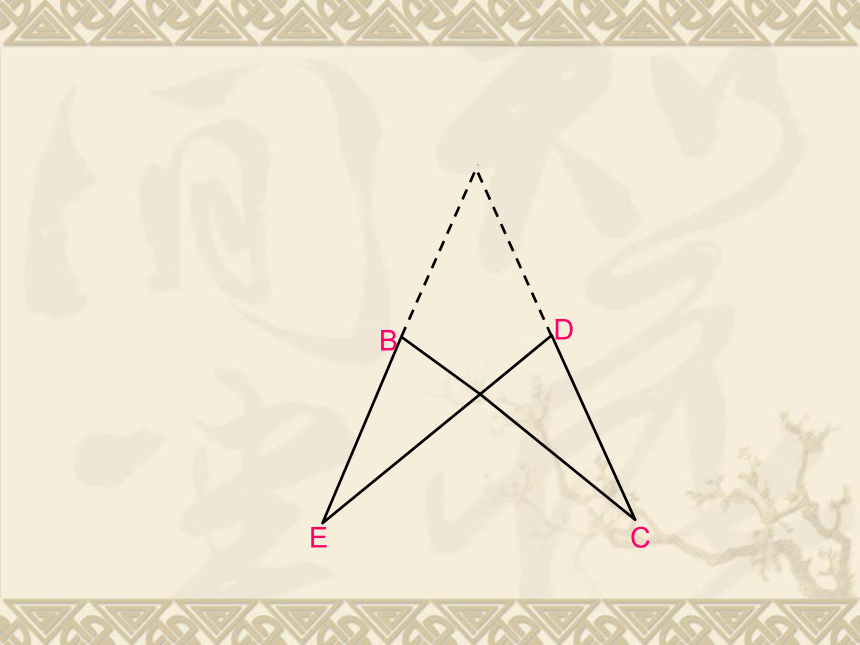
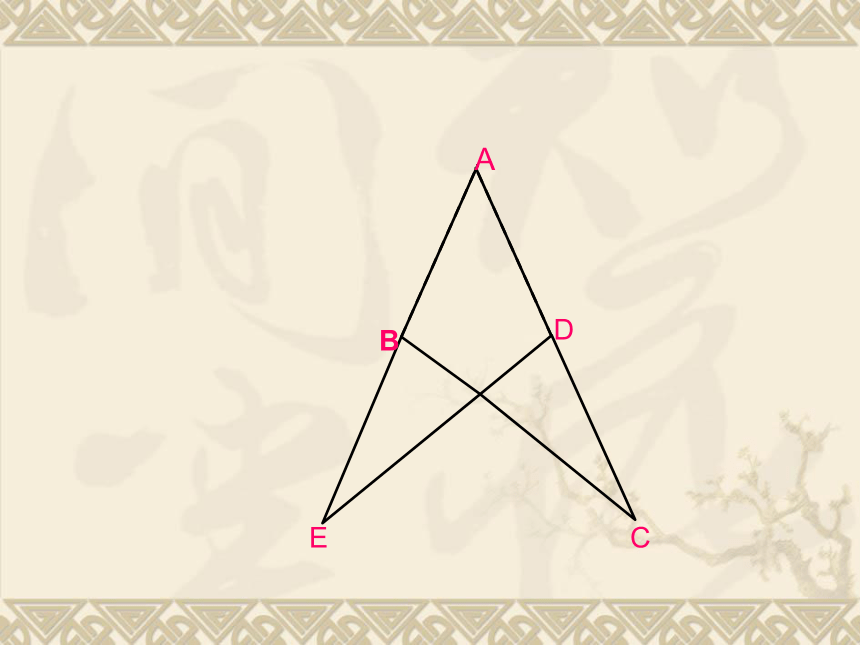
试说明AC=AD的理由。1、已知:AE=AC,
要想△ABC≌△ADE,应添加什么条件?2、已知:AB=AD,BC=DE;
要想 △ABC≌△ADE,应添加什么条件?3、已知:∠B=∠D,∠C=∠E;
要想△ABC≌△ADE,应添加什么条件?C ′ACBDA’B’D’例6 已知:△ABC≌△A’B’C’,AD、A’D’分别是△ABC, △A’B’C’的高;试说明 AD=A’D’的理由。 例7 已知:如图,已知∠1=∠2,∠3=∠4,BD=CE;试说明AB=AC的理由。CBDEA例8、已知:BD⊥AC,CE⊥AB,∠1=∠2
试说明BE=CD的理由。二.课堂练习(一)1.边角边公理(SAS):∵AB=A′B′∠B=∠B′(BC=B′C′)∴△ABC≌△A’B’C′2、角边角公理(ASA):∵∠B=∠B′( BC=B′C′ )∠C=∠C′∴△ABC≌△A′B’C′.1、如图,已知△ABC≌△ABD,BC和BD是对应边,那么AC= ,∠C= 。
2、如图,△ABC≌△ADE,∠BAC=100°,
∠C=35°,那么∠EAD= ,∠E= 。DABC二.课堂练习(二)AD∠D∠CAB∠C3、△ABC和△A′B′C′的边角条件如图所示,那么这两个三角形( )A、全等;B、不全等;C、不一定全等;D、无法判定4、如图,已知BE=CF且, ∠B=∠DEF, ∠A=∠D,那么△ABC和△DEF是( )
A、全等;B、不全等;C、无法判定。CA基本题型如图:在△ABC中,AD为角平分线,DE⊥AB于E, DF⊥AC于F, AB=10cm,AC=8cm,△ABC的面积是45平方厘米,求DE的长。ABCDEF已知:AE=DF,AE//DF,CE=BF,
AB=10cm,求CD的长。已知:CD⊥AB,BE⊥AC,D、E是垂足BE、CD相交与O。
(1)当∠1=∠2时,求证:OB=OC;
(2)当0B=0C时,求证:∠1=∠2已知:AB//CD,AB=CD,求证:AE=CF二.课堂练习(三)
测量如图河的宽度,某人在河的对岸找到一参照物树木A,视线 AB与河岸垂直,然后该人沿河岸步行10步(每步约0.75M)到O处,进行标记,再向前步行10步到D处,最后背对河岸向前步行20步,此时树木A,标记O,恰好在同一视线上,则河的宽度为 米。15ABODC
