2023—2024学年人教版数学九年级下册27.2.1 相似三角形的判定 同步练习(含答案)
文档属性
| 名称 | 2023—2024学年人教版数学九年级下册27.2.1 相似三角形的判定 同步练习(含答案) | 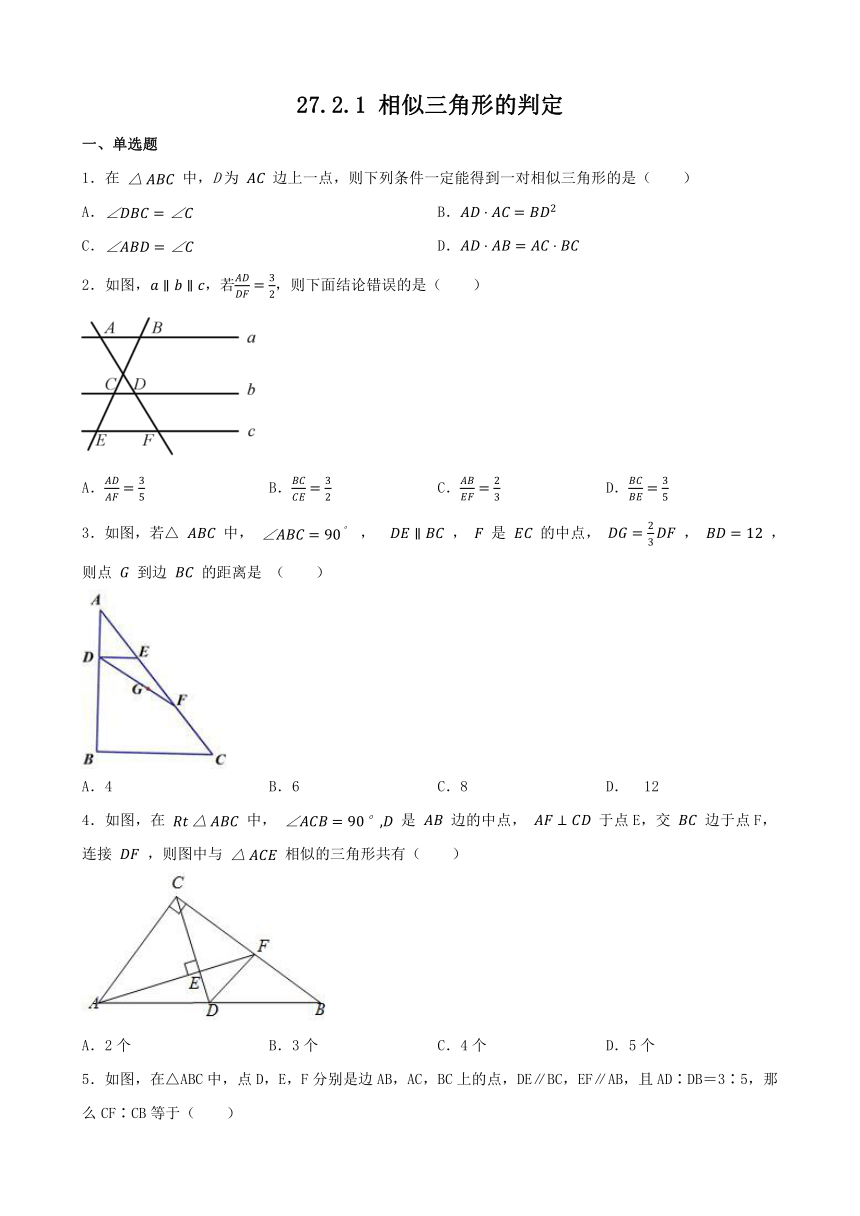 | |
| 格式 | docx | ||
| 文件大小 | 184.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-09 19:16:32 | ||
图片预览


文档简介
27.2.1 相似三角形的判定
一、单选题
1.在 中,D为 边上一点,则下列条件一定能得到一对相似三角形的是( )
A. B.
C. D.
2.如图,,若,则下面结论错误的是( )
A. B. C. D.
3.如图,若△ 中, , , 是 的中点, , ,则点 到边 的距离是 ( )
A.4 B.6 C.8 D. 12
4.如图,在 中, 是 边的中点, 于点E,交 边于点F,连接 ,则图中与 相似的三角形共有( )
A.2个 B.3个 C.4个 D.5个
5.如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD∶DB=3∶5,那么CF∶CB等于( )
A.5∶8 B.3∶8 C.3∶5 D.2∶5
6.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A,B,C和点D,E,F.若 = ,DE=4,则EF的长是( )
A. B. C.6 D.10
7.如图,在矩形 中, 在 上, ,交 于 ,连结 ,则图中与 一定相似的三角形是( )
A. B.
C. D. 和
8.李老师在编写下面这个题目的答案时,不小心打乱了解答过程的顺序,你能帮他调整过来吗?证明步骤正确的顺序是
已知:如图,在中,点D,E,F分别在边AB,AC,BC上,且,,
求证:∽.
证明:又,,,,∽.
A. B. C. D.
二、填空题
9.如图,∠1=∠2,请补充一个条件: ,使 .
10.在如图所示方格纸中,已知△DEF是由△ABC经相似变换所得的像,那么△DEF的每条边都扩大到原来的 倍.
11.如图,AD是直角△ABC (∠C=90°)的角平分线,EF⊥AD于D,与AB及AC的延长线分别交于E,F,写出图中的一对全等三角形是 ;一对相似三角形是 .
12.如图,在平面直角坐标系中有两点A(4,0),B(0,2),如果点C在x轴上(C与A不重合)当点C的坐标为 时,使得△BOC∽△AOB.
13.如图,在等腰 中, ,点P在 的延长线上, ,点D在 边上, ,则 的值是 .
三、解答题
14.如图所示,在△ABC中,EF∥CD,DE∥BC,求证:AF:FD=AD:DB.
15.如图,在中,为边上一点,.求证:.
16.如图,点P在平行四边形ABCD的CD边上,连接BP并延长与AD的延长线交于点Q.
(1)求证:△DQP∽△CBP;
(2)当△DQP≌△CBP,且AB=8时,求DP的长.
17.如图,在矩形 中,O是对角线 与 的交点, ,垂足为点E,已知 .
(1)求证: ;
(2)若 ,求 的长.
18.△ABC中,点D是BC边上的一点,点F在AD上,连接BF并延长交AC于点E;
(1)如图1,若D为BC的中点, ,求证:AF=FD;
(2)尺规作图:在图2中,请利用圆规和无刻度的直尺在AC上找一点E,使得 ;
(3)若F为AD的中点,设 ,请求出m、n之间的等量关系.
参考答案
1.C
2.C
3.C
4.B
5.A
6.C
7.B
8.B
9.∠E=∠C(答案不唯一)
10.2
11.△AED≌△AFD;△AED∽△DFC
12.(1,0)或(﹣1,0)
13.
14.证明:∵EF∥CD,DE∥BC,
∴
∴
∴AF:FD=AD:DB.
15.证明:∵
∴,,
∴,
又∵
∴
16.解:(1)证明:∵四边形ABCD是平行四边形,
∴AQ∥BC,
∴∠QDP=∠BCP,
又∠QPD=∠CPB,
∴△DQP∽△CBP;
(2)解:∵△DQP≌△CBP,
∴DP=CP=CD,
∵AB=CD=8,
∴DP=4.
17.(1)证明:
∵四边形 是矩形
∴ ,
∴
∵ ,
∴
∴
∴
(2)解:∵ ,
∴ ,
∴
∵ ,
∴
∵O是对角线 与 的交点
∴ ,
∴
∴ 为等边三角形,
∴
∵ ,
∴
18.(1)解:作DG∥BE交AC于G,
∵DG∥BE,BD=CD,
∴ = =1,
∴EG=CG,
∵EF∥DG,
∴ = ,
∵ ,EG=GC,
∴ =1,
∴ =1.
∴AF=FD;
(2)解:作△ABC的中线AD,再作AD中点,连接BF并延长交AC于点E,点E即是所求;
(3)解:作DG∥BE交AC于G.
∵DG∥BE,
∴ = = ,
∵ ,设AC=a,AE=an,EC=a-an,EG=m (a-an),
∵EF∥DG,
∴ = ,
∵F为AD的中点,
∴ 即
一、单选题
1.在 中,D为 边上一点,则下列条件一定能得到一对相似三角形的是( )
A. B.
C. D.
2.如图,,若,则下面结论错误的是( )
A. B. C. D.
3.如图,若△ 中, , , 是 的中点, , ,则点 到边 的距离是 ( )
A.4 B.6 C.8 D. 12
4.如图,在 中, 是 边的中点, 于点E,交 边于点F,连接 ,则图中与 相似的三角形共有( )
A.2个 B.3个 C.4个 D.5个
5.如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD∶DB=3∶5,那么CF∶CB等于( )
A.5∶8 B.3∶8 C.3∶5 D.2∶5
6.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A,B,C和点D,E,F.若 = ,DE=4,则EF的长是( )
A. B. C.6 D.10
7.如图,在矩形 中, 在 上, ,交 于 ,连结 ,则图中与 一定相似的三角形是( )
A. B.
C. D. 和
8.李老师在编写下面这个题目的答案时,不小心打乱了解答过程的顺序,你能帮他调整过来吗?证明步骤正确的顺序是
已知:如图,在中,点D,E,F分别在边AB,AC,BC上,且,,
求证:∽.
证明:又,,,,∽.
A. B. C. D.
二、填空题
9.如图,∠1=∠2,请补充一个条件: ,使 .
10.在如图所示方格纸中,已知△DEF是由△ABC经相似变换所得的像,那么△DEF的每条边都扩大到原来的 倍.
11.如图,AD是直角△ABC (∠C=90°)的角平分线,EF⊥AD于D,与AB及AC的延长线分别交于E,F,写出图中的一对全等三角形是 ;一对相似三角形是 .
12.如图,在平面直角坐标系中有两点A(4,0),B(0,2),如果点C在x轴上(C与A不重合)当点C的坐标为 时,使得△BOC∽△AOB.
13.如图,在等腰 中, ,点P在 的延长线上, ,点D在 边上, ,则 的值是 .
三、解答题
14.如图所示,在△ABC中,EF∥CD,DE∥BC,求证:AF:FD=AD:DB.
15.如图,在中,为边上一点,.求证:.
16.如图,点P在平行四边形ABCD的CD边上,连接BP并延长与AD的延长线交于点Q.
(1)求证:△DQP∽△CBP;
(2)当△DQP≌△CBP,且AB=8时,求DP的长.
17.如图,在矩形 中,O是对角线 与 的交点, ,垂足为点E,已知 .
(1)求证: ;
(2)若 ,求 的长.
18.△ABC中,点D是BC边上的一点,点F在AD上,连接BF并延长交AC于点E;
(1)如图1,若D为BC的中点, ,求证:AF=FD;
(2)尺规作图:在图2中,请利用圆规和无刻度的直尺在AC上找一点E,使得 ;
(3)若F为AD的中点,设 ,请求出m、n之间的等量关系.
参考答案
1.C
2.C
3.C
4.B
5.A
6.C
7.B
8.B
9.∠E=∠C(答案不唯一)
10.2
11.△AED≌△AFD;△AED∽△DFC
12.(1,0)或(﹣1,0)
13.
14.证明:∵EF∥CD,DE∥BC,
∴
∴
∴AF:FD=AD:DB.
15.证明:∵
∴,,
∴,
又∵
∴
16.解:(1)证明:∵四边形ABCD是平行四边形,
∴AQ∥BC,
∴∠QDP=∠BCP,
又∠QPD=∠CPB,
∴△DQP∽△CBP;
(2)解:∵△DQP≌△CBP,
∴DP=CP=CD,
∵AB=CD=8,
∴DP=4.
17.(1)证明:
∵四边形 是矩形
∴ ,
∴
∵ ,
∴
∴
∴
(2)解:∵ ,
∴ ,
∴
∵ ,
∴
∵O是对角线 与 的交点
∴ ,
∴
∴ 为等边三角形,
∴
∵ ,
∴
18.(1)解:作DG∥BE交AC于G,
∵DG∥BE,BD=CD,
∴ = =1,
∴EG=CG,
∵EF∥DG,
∴ = ,
∵ ,EG=GC,
∴ =1,
∴ =1.
∴AF=FD;
(2)解:作△ABC的中线AD,再作AD中点,连接BF并延长交AC于点E,点E即是所求;
(3)解:作DG∥BE交AC于G.
∵DG∥BE,
∴ = = ,
∵ ,设AC=a,AE=an,EC=a-an,EG=m (a-an),
∵EF∥DG,
∴ = ,
∵F为AD的中点,
∴ 即
