四川省绵阳市江油市太白中学2023-2024学年高二上学期期中考试数学试题(含答案)
文档属性
| 名称 | 四川省绵阳市江油市太白中学2023-2024学年高二上学期期中考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 484.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-08 17:47:31 | ||
图片预览



文档简介
太白中学2023-2024学年高二上学期期中考试
数学试卷
总分:150分 考试时间:150分钟
一、单选题
1. 某学校高二年级选择“史政地”,“史政生”和“史地生”组合的同学人数分别为210,90和60.现采用分层抽样的方法选出12位同学进行项调查研究,则“史政生”组合中选出的同学人数为( )
A. 7 B. 6 C. 3 D. 2
2. 已知一组数据从小到大为4,5,6,8,,13,18,30,若这组数据的分位数是中位数的两倍,则( )
A. 12 B. 11 C. 10 D. 9
3. 抛郑两枚质地均匀的硬币,设事件“第一枚硬币反面向上”,事件“第二枚硬币正面向上”,下列结论中正确的是( )
A. 与为互斥事件 B.
C. 与为相互独立事件 D. 与互为对立事件
4. 某学校为了解高三年级学生在线学习情况,统计了2020年4月18日—27日(共10天)他们在线学习人数及其增长比例数据,并制成如图所示的条形图与折线图的组合图.
根据组合图判断,下列结论正确的是( )
A. 这10天学生在线学习人数的增长比例在逐日增加
B. 前5天在线学习人数的方差大于后5天在线学习人数的方差
C. 这10天学生在线学习人数在逐日增加
D. 前5天在线学习人数增长比例的极差大于后5天在线学习人数增长比例的极差
5. 已知直线l过定点,且方向向量为,则点到l的距离为( )
A. B. C. D.
6. 齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现双方各出上、中、下等马各一匹分组分别进行一场比赛,胜两场及以上者获胜,若双方均不知道对方马的出场顺序,则田忌获胜的概率为( )
A. B.
C. D.
7. 《几何原本》是古希腊数学家欧几里得一部不朽之作,其第十一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥.如图,、是直角圆锥的两个轴截面,且,则异面直线与所成角的余弦值为( )
A. B. C. D.
8. 在长方体中,,,O是AC的中点,点P在线段上,若直线OP与平面所成的角为,则的取值范围是( )
A. B. C. D.
二、多选题
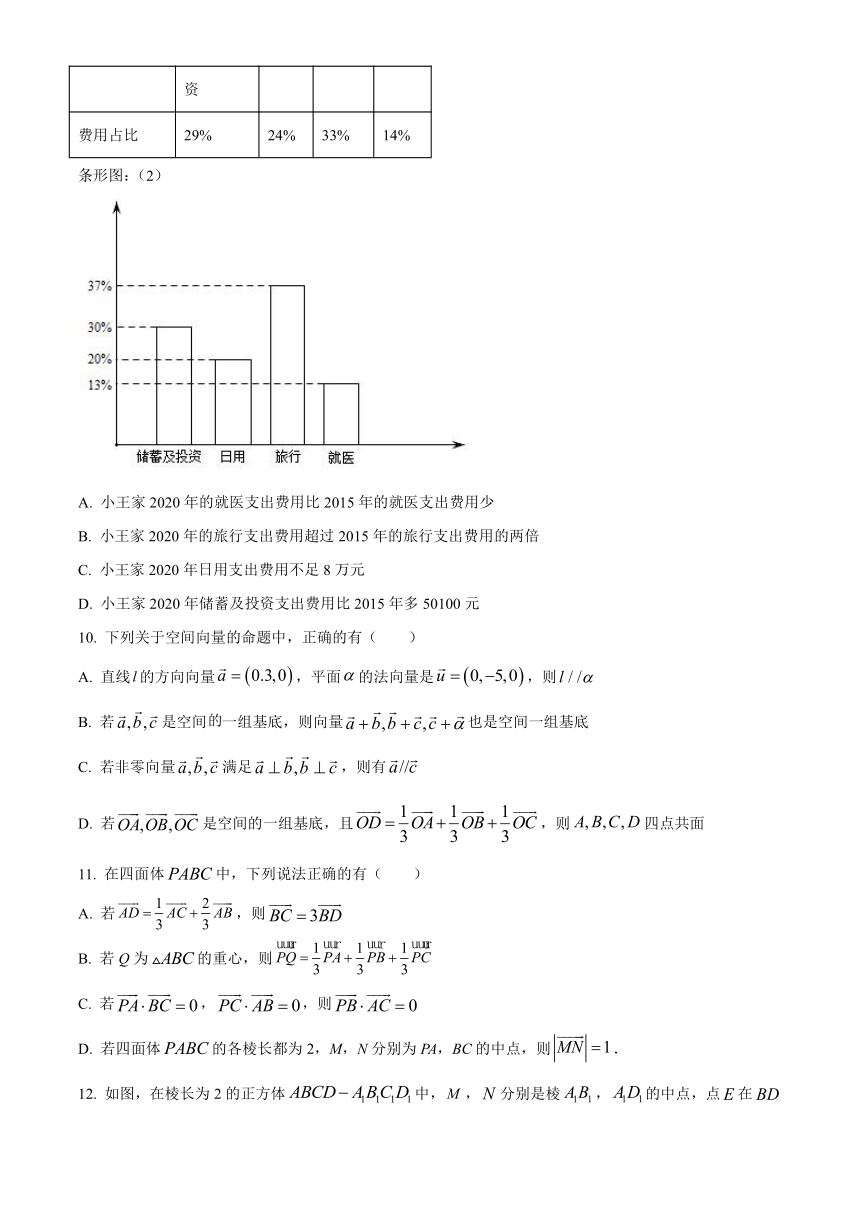
9. 2021年7月1日,习近平总书记在庆祝中国共产党成立100周年大会上庄严宣告:“经过全党全国各族人民持续奋斗,我们实现了第一个百年奋斗目标,在中华大地上全面建成了小康社会,历史性地解决了绝对贫困问题,正在意气风发向着全面建成社会主义现代化强国的第二个百年奋斗目标迈进.”东南沿海某二线城市的小王家.2015年总收入210000,2020年总收入370000元,2015年各项支出如表(1),2020年各项支出如条形图(2),则下列说法正确的是( )
表:(1)
可支配收入 储蓄及投资 日用 旅行 就医
费用占比 29% 24% 33% 14%
条形图:(2)
A. 小王家2020年的就医支出费用比2015年的就医支出费用少
B. 小王家2020年的旅行支出费用超过2015年的旅行支出费用的两倍
C. 小王家2020年日用支出费用不足8万元
D. 小王家2020年储蓄及投资支出费用比2015年多50100元
10. 下列关于空间向量的命题中,正确的有( )
A. 直线的方向向量,平面的法向量是,则
B. 若是空间一组基底,则向量也是空间一组基底
C. 若非零向量满足,则有
D. 若是空间的一组基底,且,则四点共面
11. 在四面体中,下列说法正确的有( )
A. 若,则
B. 若Q为的重心,则
C. 若,,则
D. 若四面体的各棱长都为2,M,N分别为PA,BC的中点,则.
12. 如图,在棱长为2的正方体中,,分别是棱,的中点,点在上,点在上,且,点在线段上运动,下列说法正确的有( )
A. 当点是中点时,直线平面;
B. 直线到平面的距离是;
C. 存在点,使得;
D. 面积的最小值是
三、填空题
13. 已知样本数据都为正数,其方差,则样本数据、、、、平均数为______.
14. 为深入学习宣传贯彻党的二十大精神,某校团委举办“强国复兴有我”——党的二十大精神知识竞答活动.某场比赛中,甲、乙、丙三位同学同时回答一道有关二十大精神知识的问题.已知甲同学答对的概率是,甲、丙两位同学都答错的概率是,乙、丙两位同学都答对的概率是.若各同学答题正确与否互不影响.则甲、乙、丙三位同学中至少2位同学答对这道题的概率为______________.
15. 在棱长为的正方体中,点在侧面内,是的中点,若,则的面积的最小值为_________________.
16. 在空间直角坐标系中,,,,点H在平面内,则当取最小时,点H坐标是______.
三、解答题
17. 如图,空间四边形中,,,,点分别在上,且,.
(1)以为一组基底表示向量;
(2)求的长度.
18. 已知空间三点,,,设,.
(1)求,夹角的余弦值;
(2)若与的夹角是钝角,求k的取值范围.
19. 为了解某市家庭用电量的情况,该市统计局调查了100户居民去年一年的月均用电量,发现他们的用电量都在50至350之间,进行适当分组后,画出频率分布直方图如图所示.
(1)求a的值;
(2)求被调查用户中,用电量大于250的户数;
(3)为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯定价,其中第一档是用电不大于m时,按原始价格收费,超过m时,将提高收费价格标准.市政府希望使80%的居民缴费位于第一档,即做到80%的用户能按原有价格缴费,请给出第一档用电标准m(单位:)(精确到小数点后一位)的建议,并简要说明理由.
20. 如图,直三棱柱中,.
(1)求证:平面平面;
(2)求直线与平面所成角的余弦值.
21. 作为世界乒坛本赛季收官战,首届世界乒乓球职业大联盟世界杯总决赛年月日在新加坡结束男女单打决赛的较量,国乒包揽双冠成为最大赢家.我市男子乒乓球队为备战下届市运会,在某训练基地进行封闭式训练,甲、乙两位队员进行对抗赛,每局依次轮流发球,连续赢个球者获胜,通过分析甲、乙过去对抗赛的数据知,甲发球甲赢的概率为,乙发球甲赢的概率为,不同球的结果互不影响,已知某局甲先发球.
(1)求该局打个球甲赢的概率;
(2)求该局打个球结束的概率.
22. 如图,在三棱锥中,,,,分别为,的中点,为正三角形,平面平面.
(1)求点到平面的距离;
(2)在线段上是否存在异于端点的点,使得平面和平面夹角的余弦值为?若存在,确定点的位置;若不存在,说明理由.
太白中学2023-2024学年高二上学期期中考试
数学试卷 简要答案
一、单选题
【1题答案】
【答案】C
【2题答案】
【答案】C
【3题答案】
【答案】C
【4题答案】
【答案】C
【5题答案】
【答案】A
【6题答案】
【答案】D
【7题答案】
【答案】B
【8题答案】
【答案】D
二、多选题
【9题答案】
【答案】CD
【10题答案】
【答案】BD
【11题答案】
【答案】ABC
【12题答案】
【答案】AC
三、填空题
【13题答案】
【答案】11
【14题答案】
【答案】
【15题答案】
【答案】
【16题答案】
【答案】
三、解答题
【17题答案】
【答案】(1)
(2)
【18题答案】
【答案】(1)
(2)
【19题答案】
【答案】(1)
(2)户
(3),理由略
【20题答案】
【答案】(1)证明略.
(2)
【21题答案】
【答案】(1)
(2)
【22题答案】
【答案】(1)
(2)存在点,使得平面和平面夹角的余弦值为,此时为中点
数学试卷
总分:150分 考试时间:150分钟
一、单选题
1. 某学校高二年级选择“史政地”,“史政生”和“史地生”组合的同学人数分别为210,90和60.现采用分层抽样的方法选出12位同学进行项调查研究,则“史政生”组合中选出的同学人数为( )
A. 7 B. 6 C. 3 D. 2
2. 已知一组数据从小到大为4,5,6,8,,13,18,30,若这组数据的分位数是中位数的两倍,则( )
A. 12 B. 11 C. 10 D. 9
3. 抛郑两枚质地均匀的硬币,设事件“第一枚硬币反面向上”,事件“第二枚硬币正面向上”,下列结论中正确的是( )
A. 与为互斥事件 B.
C. 与为相互独立事件 D. 与互为对立事件
4. 某学校为了解高三年级学生在线学习情况,统计了2020年4月18日—27日(共10天)他们在线学习人数及其增长比例数据,并制成如图所示的条形图与折线图的组合图.
根据组合图判断,下列结论正确的是( )
A. 这10天学生在线学习人数的增长比例在逐日增加
B. 前5天在线学习人数的方差大于后5天在线学习人数的方差
C. 这10天学生在线学习人数在逐日增加
D. 前5天在线学习人数增长比例的极差大于后5天在线学习人数增长比例的极差
5. 已知直线l过定点,且方向向量为,则点到l的距离为( )
A. B. C. D.
6. 齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现双方各出上、中、下等马各一匹分组分别进行一场比赛,胜两场及以上者获胜,若双方均不知道对方马的出场顺序,则田忌获胜的概率为( )
A. B.
C. D.
7. 《几何原本》是古希腊数学家欧几里得一部不朽之作,其第十一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥.如图,、是直角圆锥的两个轴截面,且,则异面直线与所成角的余弦值为( )
A. B. C. D.
8. 在长方体中,,,O是AC的中点,点P在线段上,若直线OP与平面所成的角为,则的取值范围是( )
A. B. C. D.
二、多选题
9. 2021年7月1日,习近平总书记在庆祝中国共产党成立100周年大会上庄严宣告:“经过全党全国各族人民持续奋斗,我们实现了第一个百年奋斗目标,在中华大地上全面建成了小康社会,历史性地解决了绝对贫困问题,正在意气风发向着全面建成社会主义现代化强国的第二个百年奋斗目标迈进.”东南沿海某二线城市的小王家.2015年总收入210000,2020年总收入370000元,2015年各项支出如表(1),2020年各项支出如条形图(2),则下列说法正确的是( )
表:(1)
可支配收入 储蓄及投资 日用 旅行 就医
费用占比 29% 24% 33% 14%
条形图:(2)
A. 小王家2020年的就医支出费用比2015年的就医支出费用少
B. 小王家2020年的旅行支出费用超过2015年的旅行支出费用的两倍
C. 小王家2020年日用支出费用不足8万元
D. 小王家2020年储蓄及投资支出费用比2015年多50100元
10. 下列关于空间向量的命题中,正确的有( )
A. 直线的方向向量,平面的法向量是,则
B. 若是空间一组基底,则向量也是空间一组基底
C. 若非零向量满足,则有
D. 若是空间的一组基底,且,则四点共面
11. 在四面体中,下列说法正确的有( )
A. 若,则
B. 若Q为的重心,则
C. 若,,则
D. 若四面体的各棱长都为2,M,N分别为PA,BC的中点,则.
12. 如图,在棱长为2的正方体中,,分别是棱,的中点,点在上,点在上,且,点在线段上运动,下列说法正确的有( )
A. 当点是中点时,直线平面;
B. 直线到平面的距离是;
C. 存在点,使得;
D. 面积的最小值是
三、填空题
13. 已知样本数据都为正数,其方差,则样本数据、、、、平均数为______.
14. 为深入学习宣传贯彻党的二十大精神,某校团委举办“强国复兴有我”——党的二十大精神知识竞答活动.某场比赛中,甲、乙、丙三位同学同时回答一道有关二十大精神知识的问题.已知甲同学答对的概率是,甲、丙两位同学都答错的概率是,乙、丙两位同学都答对的概率是.若各同学答题正确与否互不影响.则甲、乙、丙三位同学中至少2位同学答对这道题的概率为______________.
15. 在棱长为的正方体中,点在侧面内,是的中点,若,则的面积的最小值为_________________.
16. 在空间直角坐标系中,,,,点H在平面内,则当取最小时,点H坐标是______.
三、解答题
17. 如图,空间四边形中,,,,点分别在上,且,.
(1)以为一组基底表示向量;
(2)求的长度.
18. 已知空间三点,,,设,.
(1)求,夹角的余弦值;
(2)若与的夹角是钝角,求k的取值范围.
19. 为了解某市家庭用电量的情况,该市统计局调查了100户居民去年一年的月均用电量,发现他们的用电量都在50至350之间,进行适当分组后,画出频率分布直方图如图所示.
(1)求a的值;
(2)求被调查用户中,用电量大于250的户数;
(3)为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯定价,其中第一档是用电不大于m时,按原始价格收费,超过m时,将提高收费价格标准.市政府希望使80%的居民缴费位于第一档,即做到80%的用户能按原有价格缴费,请给出第一档用电标准m(单位:)(精确到小数点后一位)的建议,并简要说明理由.
20. 如图,直三棱柱中,.
(1)求证:平面平面;
(2)求直线与平面所成角的余弦值.
21. 作为世界乒坛本赛季收官战,首届世界乒乓球职业大联盟世界杯总决赛年月日在新加坡结束男女单打决赛的较量,国乒包揽双冠成为最大赢家.我市男子乒乓球队为备战下届市运会,在某训练基地进行封闭式训练,甲、乙两位队员进行对抗赛,每局依次轮流发球,连续赢个球者获胜,通过分析甲、乙过去对抗赛的数据知,甲发球甲赢的概率为,乙发球甲赢的概率为,不同球的结果互不影响,已知某局甲先发球.
(1)求该局打个球甲赢的概率;
(2)求该局打个球结束的概率.
22. 如图,在三棱锥中,,,,分别为,的中点,为正三角形,平面平面.
(1)求点到平面的距离;
(2)在线段上是否存在异于端点的点,使得平面和平面夹角的余弦值为?若存在,确定点的位置;若不存在,说明理由.
太白中学2023-2024学年高二上学期期中考试
数学试卷 简要答案
一、单选题
【1题答案】
【答案】C
【2题答案】
【答案】C
【3题答案】
【答案】C
【4题答案】
【答案】C
【5题答案】
【答案】A
【6题答案】
【答案】D
【7题答案】
【答案】B
【8题答案】
【答案】D
二、多选题
【9题答案】
【答案】CD
【10题答案】
【答案】BD
【11题答案】
【答案】ABC
【12题答案】
【答案】AC
三、填空题
【13题答案】
【答案】11
【14题答案】
【答案】
【15题答案】
【答案】
【16题答案】
【答案】
三、解答题
【17题答案】
【答案】(1)
(2)
【18题答案】
【答案】(1)
(2)
【19题答案】
【答案】(1)
(2)户
(3),理由略
【20题答案】
【答案】(1)证明略.
(2)
【21题答案】
【答案】(1)
(2)
【22题答案】
【答案】(1)
(2)存在点,使得平面和平面夹角的余弦值为,此时为中点
同课章节目录
