第四章一次函数 单元练习题 (无答案)北师大版八年级数学上册
文档属性
| 名称 | 第四章一次函数 单元练习题 (无答案)北师大版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 132.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-09 22:44:41 | ||
图片预览

文档简介
第四章一次函数 单元练习题
一、单选题
1.下列函数中,是一次函数的是( )
A. B. C. D.
2.一次函数的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知点(-5,y1),(1,0),(6,y2)都在一次函数y=kx-2的图象上,则y1,y2,0的大小关系是( )
A.0<y1<y2 B.y1<0<y2 C.y1<y2<0 D.y2<0<y1
4.在下列四组点中,可以在同一个正比例函数图象上的一组点是( )
A.(2,﹣3),(﹣4,6) B.(﹣2,3),(4,6)
C.(﹣2,﹣3),(4,﹣6) D.(2,3),(﹣4,6)
5.从A地向B地打长途电话,按时收费,3分钟内收费2.4元,以后每超过1分钟加收1元,若通话t分钟(t≥3),则需付电话费y(元)与t(分钟)之间的函数关系式是( )
A.y=t﹣0.5 B.y=t﹣0.6 C.y=3.4t﹣7.8 D.y=3.4t﹣8
6.若等腰三角形的周长为20cm,底边长为xcm,一腰长为ycm,则y与x的函数表达式正确的是( )
A.y=20﹣2x(0<x<20) B.y=20﹣2x(0<x<10)
C.y=(20﹣x)(0<x<20) D.y=(20﹣x)(0<x<10)
7.下列函数中,自变量x的取值范围是x≥3的是( )
A.y= B.y= C.y=x-3 D.y=
8.已知点 都在直线 上,则 , , 的大小关系是( )
A. B. C. D.
9.将一圆柱体从水中匀速提起,从如图所示开始计时,直至其下表面刚好离开水面,停止计时.用x表示圆柱体运动时间,y表示水面的高度,则y与x之间函数关系的图象大致是( )
A. B.
C. D.
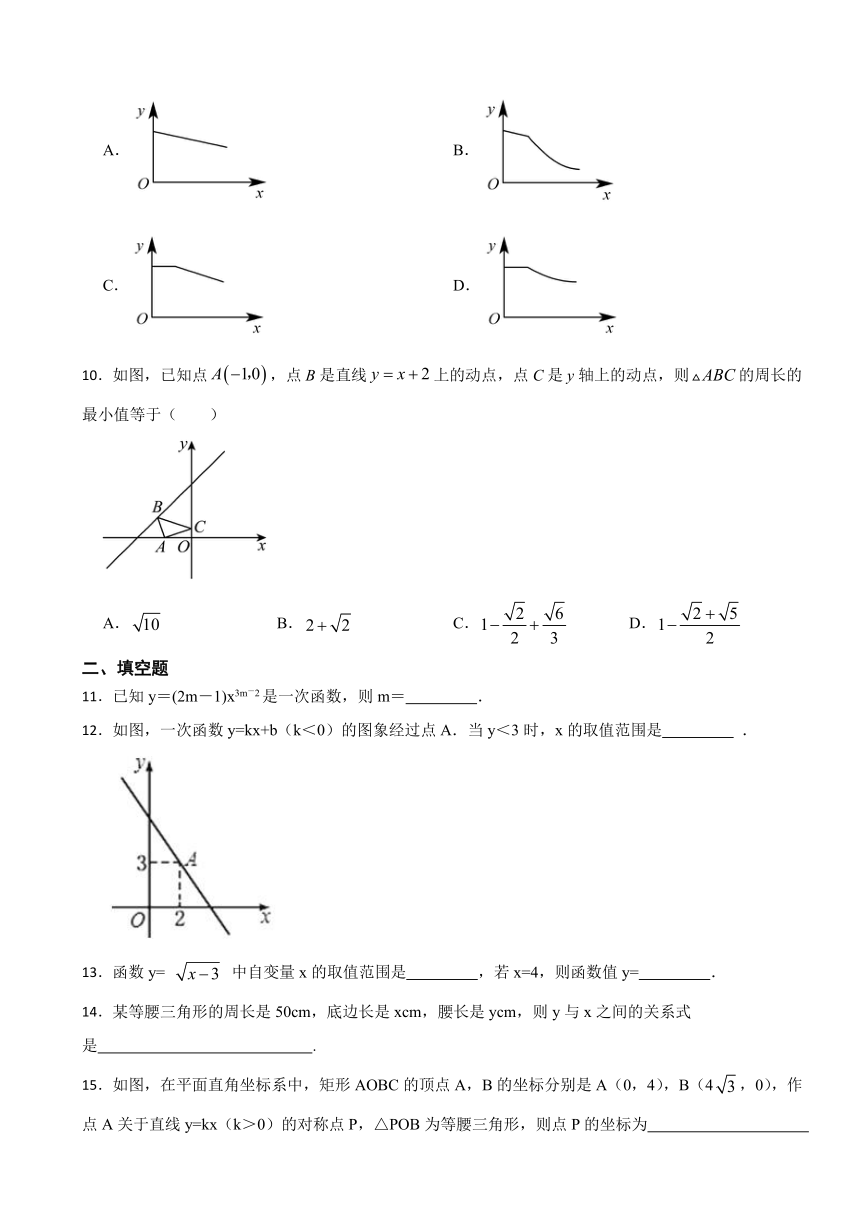
10.如图,已知点,点B是直线上的动点,点C是y轴上的动点,则的周长的最小值等于( )
A. B. C. D.
二、填空题
11.已知y=(2m-1)x3m-2是一次函数,则m= .
12.如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 .
13.函数y= 中自变量x的取值范围是 ,若x=4,则函数值y= .
14.某等腰三角形的周长是50cm,底边长是xcm,腰长是ycm,则y与x之间的关系式是 .
15.如图,在平面直角坐标系中,矩形AOBC的顶点A,B的坐标分别是A(0,4),B(4,0),作点A关于直线y=kx(k>0)的对称点P,△POB为等腰三角形,则点P的坐标为
三、解答题
16.已知函数y=(m2+m)x2m﹣1,当m取何值时;
(1)是正比例函数;
(2)是反比例函数.
17.一次函数y=﹣x+b与正比例函数y=2x图象交于点A(1,n):
(1)求一次函数解析式;
(2)将(1)中所求一次函数图象进行平行移动,平移后图象过(2,7),求平移后图象的函数解析式.
18.(1)根据画函数图象的步骤,在如图的直角坐标系中,画出函数y=|x|的图象;
(2)求证:无论m取何值,函数y=mx﹣2(m﹣1)的图象经过的一个确定的点;
(3)若(1),(2)中两图象围成图形的面积刚好为2,求m值.
19.甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途经C地时休息一小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
(1)直接写出a,m,n的值;
(2)求出甲车与B地的距离y(千米)与甲车出发时间x(小时)的函数关系式(写出自变量x的取值范围);
(3)当两车相距120千米时,乙车行驶了多长时间?
20.已知y=(k﹣3)x+k2﹣9是关于x的正比例函数,求当x=﹣4时,y的值.
21.校园美术活动社为筹备公益基金,向外出售自制环保手工艺品,A种手工艺品每件成本20元,售价30元;B种手工艺品每件成本35元,售价48元,活动社准备拿出800元作为制作成本,怎样制作才能使销售这两种手工艺品的利润最大?(其中B种商品不少于7件)
22.云南某县境内发生地震,某市积极筹集救灾物资260吨从该市区运往该县甲、乙两地,若用大、小两种货车共20辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
车 型 运往地 甲 地(元/辆) 乙 地(元/辆)
大货车 720 800
小货车 500 650
(1)求这两种货车各用多少辆?
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于132吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
23.台州市某体育用品商店一次性购进排球、足球两种商品共100个,排球每个进价40元,售价50元,足球每个进价90元,售价105元.
(1)设购进排球x个,销售完此两种商品的总利润为y元,求出y与x的函数关系式;
(2)该商家计划最多投入8000元用于购进此两种商品共100件,至少要购进多少个排球?
(3)在(2)的条件下,若售完这些商品,商家可获得最大利润是多少元?
一、单选题
1.下列函数中,是一次函数的是( )
A. B. C. D.
2.一次函数的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知点(-5,y1),(1,0),(6,y2)都在一次函数y=kx-2的图象上,则y1,y2,0的大小关系是( )
A.0<y1<y2 B.y1<0<y2 C.y1<y2<0 D.y2<0<y1
4.在下列四组点中,可以在同一个正比例函数图象上的一组点是( )
A.(2,﹣3),(﹣4,6) B.(﹣2,3),(4,6)
C.(﹣2,﹣3),(4,﹣6) D.(2,3),(﹣4,6)
5.从A地向B地打长途电话,按时收费,3分钟内收费2.4元,以后每超过1分钟加收1元,若通话t分钟(t≥3),则需付电话费y(元)与t(分钟)之间的函数关系式是( )
A.y=t﹣0.5 B.y=t﹣0.6 C.y=3.4t﹣7.8 D.y=3.4t﹣8
6.若等腰三角形的周长为20cm,底边长为xcm,一腰长为ycm,则y与x的函数表达式正确的是( )
A.y=20﹣2x(0<x<20) B.y=20﹣2x(0<x<10)
C.y=(20﹣x)(0<x<20) D.y=(20﹣x)(0<x<10)
7.下列函数中,自变量x的取值范围是x≥3的是( )
A.y= B.y= C.y=x-3 D.y=
8.已知点 都在直线 上,则 , , 的大小关系是( )
A. B. C. D.
9.将一圆柱体从水中匀速提起,从如图所示开始计时,直至其下表面刚好离开水面,停止计时.用x表示圆柱体运动时间,y表示水面的高度,则y与x之间函数关系的图象大致是( )
A. B.
C. D.
10.如图,已知点,点B是直线上的动点,点C是y轴上的动点,则的周长的最小值等于( )
A. B. C. D.
二、填空题
11.已知y=(2m-1)x3m-2是一次函数,则m= .
12.如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 .
13.函数y= 中自变量x的取值范围是 ,若x=4,则函数值y= .
14.某等腰三角形的周长是50cm,底边长是xcm,腰长是ycm,则y与x之间的关系式是 .
15.如图,在平面直角坐标系中,矩形AOBC的顶点A,B的坐标分别是A(0,4),B(4,0),作点A关于直线y=kx(k>0)的对称点P,△POB为等腰三角形,则点P的坐标为
三、解答题
16.已知函数y=(m2+m)x2m﹣1,当m取何值时;
(1)是正比例函数;
(2)是反比例函数.
17.一次函数y=﹣x+b与正比例函数y=2x图象交于点A(1,n):
(1)求一次函数解析式;
(2)将(1)中所求一次函数图象进行平行移动,平移后图象过(2,7),求平移后图象的函数解析式.
18.(1)根据画函数图象的步骤,在如图的直角坐标系中,画出函数y=|x|的图象;
(2)求证:无论m取何值,函数y=mx﹣2(m﹣1)的图象经过的一个确定的点;
(3)若(1),(2)中两图象围成图形的面积刚好为2,求m值.
19.甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途经C地时休息一小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
(1)直接写出a,m,n的值;
(2)求出甲车与B地的距离y(千米)与甲车出发时间x(小时)的函数关系式(写出自变量x的取值范围);
(3)当两车相距120千米时,乙车行驶了多长时间?
20.已知y=(k﹣3)x+k2﹣9是关于x的正比例函数,求当x=﹣4时,y的值.
21.校园美术活动社为筹备公益基金,向外出售自制环保手工艺品,A种手工艺品每件成本20元,售价30元;B种手工艺品每件成本35元,售价48元,活动社准备拿出800元作为制作成本,怎样制作才能使销售这两种手工艺品的利润最大?(其中B种商品不少于7件)
22.云南某县境内发生地震,某市积极筹集救灾物资260吨从该市区运往该县甲、乙两地,若用大、小两种货车共20辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
车 型 运往地 甲 地(元/辆) 乙 地(元/辆)
大货车 720 800
小货车 500 650
(1)求这两种货车各用多少辆?
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于132吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
23.台州市某体育用品商店一次性购进排球、足球两种商品共100个,排球每个进价40元,售价50元,足球每个进价90元,售价105元.
(1)设购进排球x个,销售完此两种商品的总利润为y元,求出y与x的函数关系式;
(2)该商家计划最多投入8000元用于购进此两种商品共100件,至少要购进多少个排球?
(3)在(2)的条件下,若售完这些商品,商家可获得最大利润是多少元?
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
