三边成比例的两个三角形相似学案
文档属性
| 名称 | 三边成比例的两个三角形相似学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 367.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-30 00:00:00 | ||
图片预览


文档简介
“一·三·六”导学案——九年级数学(下)
编号:2704 班级: 姓名:
课题:三边成比例的两个三角形相似
主备: 审核: 时间: 年 月 日
【明确目标】
1.掌握相似三角形的判定定理1.(三组对应边的比相等的两个三角形相似)
2.经历相似三角形判定定理1的探索过程,让学生体会探索的一般方法,为接下来学习其他几个定理积累一些技能,发展其推理能力.
3.会用判定定理1证明两个三角形相似.
【自主预习】
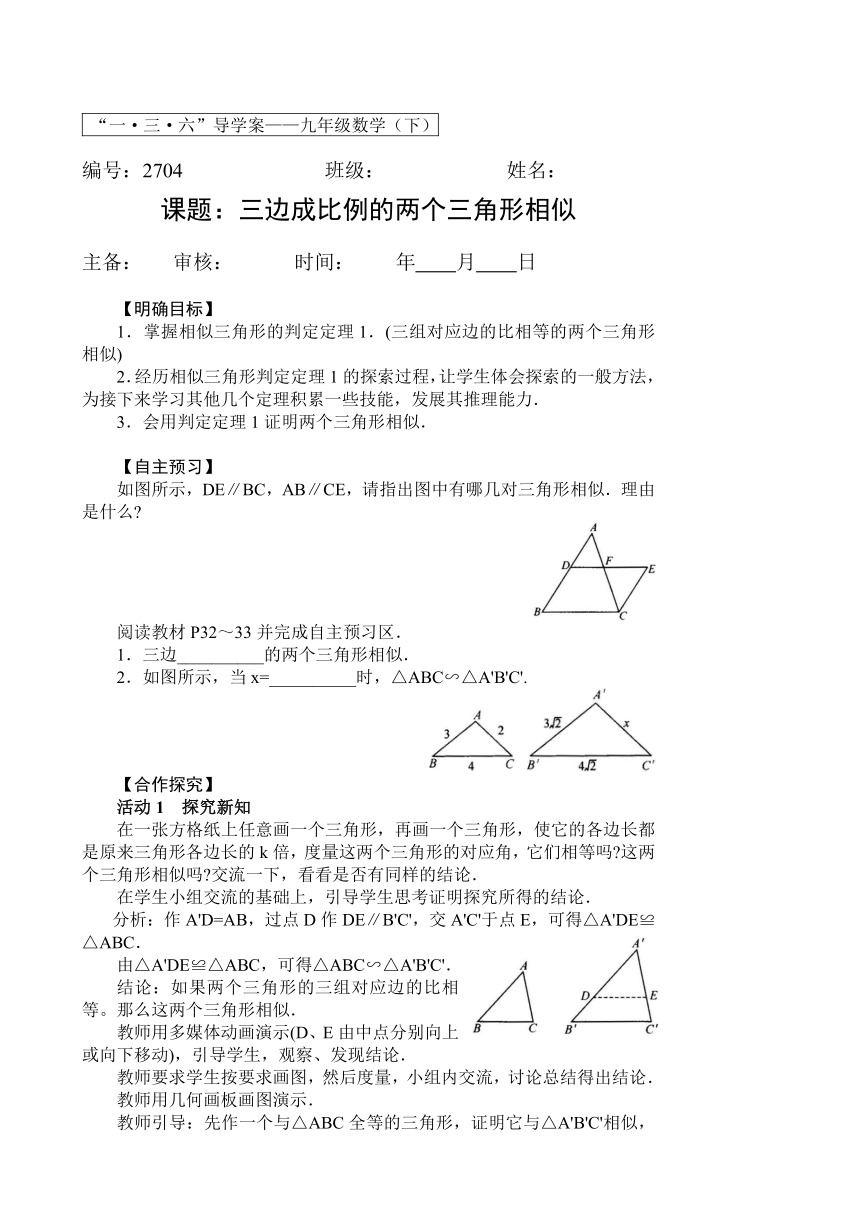
如图所示,DE∥BC,AB∥CE,请指出图中有哪几对三角形相似.理由是什么
阅读教材P32~33并完成自主预习区.
1.三边__________的两个三角形相似.
2.如图所示,当x=__________时,△ABC∽△A'B'C'.
【合作探究】
活动1 探究新知
在一张方格纸上任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗 这两个三角形相似吗 交流一下,看看是否有同样的结论.
在学生小组交流的基础上,引导学生思考证明探究所得的结论.
分析:作A'D=AB,过点D作DE∥B'C',交A'C'于点E,可得△A'DE≌△ABC.
由△A'DE≌△ABC,可得△ABC∽△A'B'C'.
结论:如果两个三角形的三组对应边的比相等。那么这两个三角形相似.
教师用多媒体动画演示(D、E由中点分别向上或向下移动),引导学生,观察、发现结论.
教师要求学生按要求画图,然后度量,小组内交流,讨论总结得出结论.
教师用几何画板画图演示.
教师引导:先作一个与△ABC全等的三角形,证明它与△A'B'C'相似,△A'DE是联系△ABC和△A'B'C'的中介.
学生先大胆猜想,然后认真观察动画演示,归纳总结结论.
学生画图、度量、交流、归纳.
学生观察动画演示.
学生探索推理过程,与同伴交流.
活动2 新知运用
如图所示,判断4×4方格中的两个三角形是否相似,并说明理由.
【当堂反馈】
教材P34练习1
知识点一 三边成比例的两个三角形相似
1.△ABC的三边长分别为,2,,△A1B1C1的两边长分别为1和. 当△A1B1C1的第三边长为__________时,△ABC和△A1B1C1相似.
2.有甲、乙两个三角形木框,甲三角形木框的三边长分别为1,,,乙三角形木框的三边长分别为5,,,则甲、乙两个三角形( )
A.一定相似 B.一定不相似
C.不一定相似 D.无法判断
3.若△ABC和△DEF满足下列条件,其中使△ABC与△DEF相似的是( )
A.AB=2,BC=3,AC=4,DE=4,EF=6,DF=8
B.AB=4,BC=6,AC=8,DE=5,EF=10,DF=15
C.AB=1,BC=3,AC=2,DE=,EF=,DF=
D.AB=1,BC=,AC=3,DE=,EF=2,DF=
知识点二 相似三角形判定的运用
4.如图,△AOB∽△COD,则x=_______,y=_______.
第4题图 第5题图
5.如图,点D在△ABC内,连接BD,并延长到点E,连接AD,AE,若∠EAC=30°,,则∠BAD=________.
6.已知△ABC的各边之比为2:3:4,与其相似的另一个△A'B'C'中的最小边长为4cm,试求其他两边之长.
【拓展提升】
(1)如图所示,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当CM=__________时,△AED与以M、N、C为顶点的三角形相似.
(2)如图所示,在△ABC中,∠A=60°,BD⊥AC,CE⊥AB,求证:△ADE∽△ABC.
【课后检测】
一、选择题
1.已知△ABC中,AB=10,BC=8,AC=6,另一个与它相似的△A'B'C'中,A'B'=5,B'C'=4,A'C'=3,则△A'B'C'与△ABC的相似比为( )
A.2 B. C. D.
2.如图,在正方形网格上有6个三角形;①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中与①相似的是( )
A.②③④ B.③④⑤ C.④⑤⑥ D.②③⑥
二、填空题
3.如图,在正方形网格上画有梯形ABCD,则∠BDC的度数为__________.
4.一个三角形的三边长分别为3cm,4cm,5cm,另一个与它相似的三角形的一边长为2cm,则另一个三角形的另外两边长分别可以为________________________________________.
5.网格图中每个方格都是边长为1的正方形.若A,B,C,D,E,F都是格点,试说明△ABC∽△DEF.
6.阅读理解:
如图,在Rt△ABC中,AB=1.5cm,AC=2cm,BC=2.5cm;在△DEF中,DE=2.8cm,EF=2.1cm,DF=3.5cm.试判断这两个三角形是否相似.某同学解答如下:
∵,
∴≠≠,
∴两个三角形不相似.该同学判断是否正确,请写出你正确的判断.
7.一个钢筋三角架各边长分别是30cm、50cm、70cm,现在要做一个与其相似的钢筋三角架,而只有长为35cm和70cm的两根钢筋,要求以其中一根为边,从另一根上截下两段(允许有余料)作为两边,问有几种不同的截法
8.如图,已知A(3,0),B(0,4),C(4,2).作CD⊥x轴于D,连接AB,BC,AC.
(1)证明△ABC∽△ACD;
(2)计算S△ABC:S△ACD的值,看一看,这一比值与两个三角形的相似比有什么关系
编号:2704 班级: 姓名:
课题:三边成比例的两个三角形相似
主备: 审核: 时间: 年 月 日
【明确目标】
1.掌握相似三角形的判定定理1.(三组对应边的比相等的两个三角形相似)
2.经历相似三角形判定定理1的探索过程,让学生体会探索的一般方法,为接下来学习其他几个定理积累一些技能,发展其推理能力.
3.会用判定定理1证明两个三角形相似.
【自主预习】
如图所示,DE∥BC,AB∥CE,请指出图中有哪几对三角形相似.理由是什么
阅读教材P32~33并完成自主预习区.
1.三边__________的两个三角形相似.
2.如图所示,当x=__________时,△ABC∽△A'B'C'.
【合作探究】
活动1 探究新知
在一张方格纸上任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗 这两个三角形相似吗 交流一下,看看是否有同样的结论.
在学生小组交流的基础上,引导学生思考证明探究所得的结论.
分析:作A'D=AB,过点D作DE∥B'C',交A'C'于点E,可得△A'DE≌△ABC.
由△A'DE≌△ABC,可得△ABC∽△A'B'C'.
结论:如果两个三角形的三组对应边的比相等。那么这两个三角形相似.
教师用多媒体动画演示(D、E由中点分别向上或向下移动),引导学生,观察、发现结论.
教师要求学生按要求画图,然后度量,小组内交流,讨论总结得出结论.
教师用几何画板画图演示.
教师引导:先作一个与△ABC全等的三角形,证明它与△A'B'C'相似,△A'DE是联系△ABC和△A'B'C'的中介.
学生先大胆猜想,然后认真观察动画演示,归纳总结结论.
学生画图、度量、交流、归纳.
学生观察动画演示.
学生探索推理过程,与同伴交流.
活动2 新知运用
如图所示,判断4×4方格中的两个三角形是否相似,并说明理由.
【当堂反馈】
教材P34练习1
知识点一 三边成比例的两个三角形相似
1.△ABC的三边长分别为,2,,△A1B1C1的两边长分别为1和. 当△A1B1C1的第三边长为__________时,△ABC和△A1B1C1相似.
2.有甲、乙两个三角形木框,甲三角形木框的三边长分别为1,,,乙三角形木框的三边长分别为5,,,则甲、乙两个三角形( )
A.一定相似 B.一定不相似
C.不一定相似 D.无法判断
3.若△ABC和△DEF满足下列条件,其中使△ABC与△DEF相似的是( )
A.AB=2,BC=3,AC=4,DE=4,EF=6,DF=8
B.AB=4,BC=6,AC=8,DE=5,EF=10,DF=15
C.AB=1,BC=3,AC=2,DE=,EF=,DF=
D.AB=1,BC=,AC=3,DE=,EF=2,DF=
知识点二 相似三角形判定的运用
4.如图,△AOB∽△COD,则x=_______,y=_______.
第4题图 第5题图
5.如图,点D在△ABC内,连接BD,并延长到点E,连接AD,AE,若∠EAC=30°,,则∠BAD=________.
6.已知△ABC的各边之比为2:3:4,与其相似的另一个△A'B'C'中的最小边长为4cm,试求其他两边之长.
【拓展提升】
(1)如图所示,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当CM=__________时,△AED与以M、N、C为顶点的三角形相似.
(2)如图所示,在△ABC中,∠A=60°,BD⊥AC,CE⊥AB,求证:△ADE∽△ABC.
【课后检测】
一、选择题
1.已知△ABC中,AB=10,BC=8,AC=6,另一个与它相似的△A'B'C'中,A'B'=5,B'C'=4,A'C'=3,则△A'B'C'与△ABC的相似比为( )
A.2 B. C. D.
2.如图,在正方形网格上有6个三角形;①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中与①相似的是( )
A.②③④ B.③④⑤ C.④⑤⑥ D.②③⑥
二、填空题
3.如图,在正方形网格上画有梯形ABCD,则∠BDC的度数为__________.
4.一个三角形的三边长分别为3cm,4cm,5cm,另一个与它相似的三角形的一边长为2cm,则另一个三角形的另外两边长分别可以为________________________________________.
5.网格图中每个方格都是边长为1的正方形.若A,B,C,D,E,F都是格点,试说明△ABC∽△DEF.
6.阅读理解:
如图,在Rt△ABC中,AB=1.5cm,AC=2cm,BC=2.5cm;在△DEF中,DE=2.8cm,EF=2.1cm,DF=3.5cm.试判断这两个三角形是否相似.某同学解答如下:
∵,
∴≠≠,
∴两个三角形不相似.该同学判断是否正确,请写出你正确的判断.
7.一个钢筋三角架各边长分别是30cm、50cm、70cm,现在要做一个与其相似的钢筋三角架,而只有长为35cm和70cm的两根钢筋,要求以其中一根为边,从另一根上截下两段(允许有余料)作为两边,问有几种不同的截法
8.如图,已知A(3,0),B(0,4),C(4,2).作CD⊥x轴于D,连接AB,BC,AC.
(1)证明△ABC∽△ACD;
(2)计算S△ABC:S△ACD的值,看一看,这一比值与两个三角形的相似比有什么关系
