两边成比例且夹角相等的两个三角形相似学案
文档属性
| 名称 | 两边成比例且夹角相等的两个三角形相似学案 | 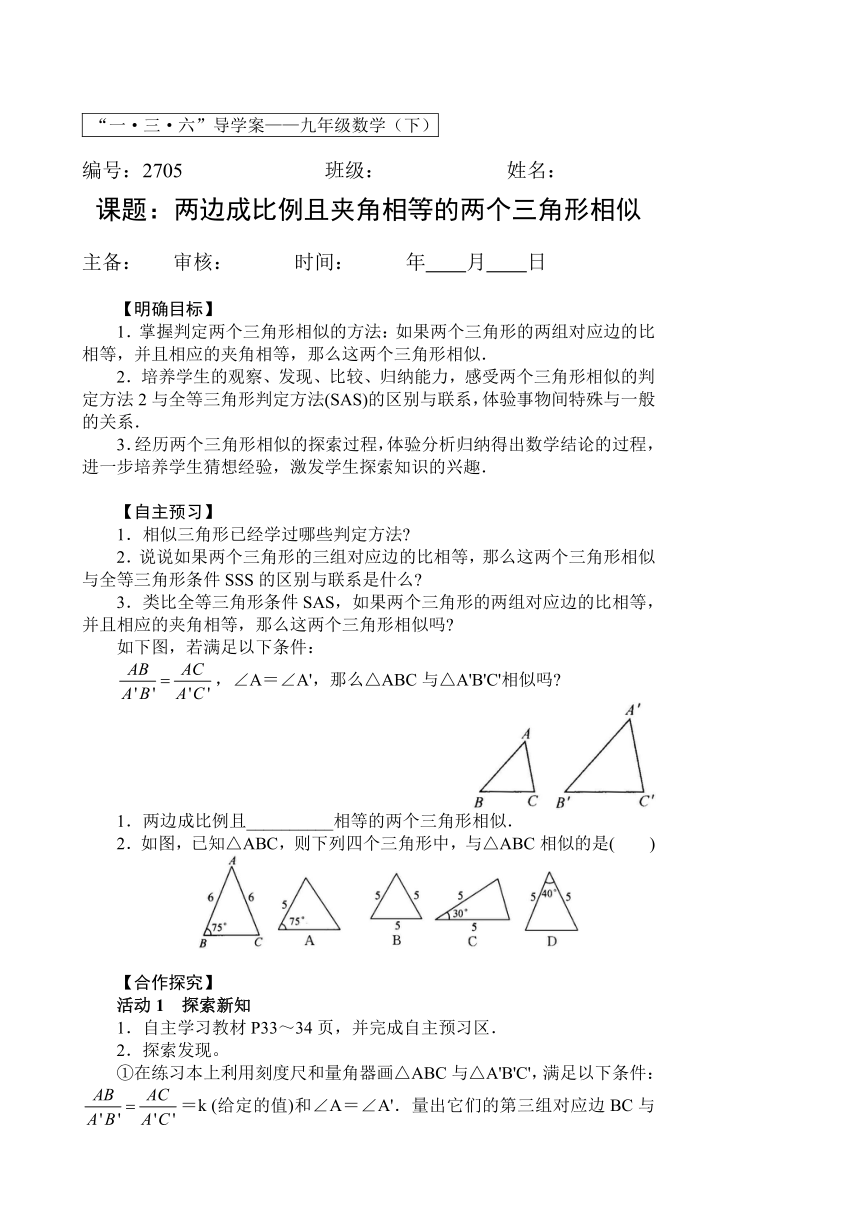 | |
| 格式 | zip | ||
| 文件大小 | 352.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-30 21:05:20 | ||
图片预览


文档简介
“一·三·六”导学案——九年级数学(下)
编号:2705 班级: 姓名:
课题:两边成比例且夹角相等的两个三角形相似
主备: 审核: 时间: 年 月 日
【明确目标】
1.掌握判定两个三角形相似的方法:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
2.培养学生的观察、发现、比较、归纳能力,感受两个三角形相似的判定方法2与全等三角形判定方法(SAS)的区别与联系,体验事物间特殊与一般的关系.
3.经历两个三角形相似的探索过程,体验分析归纳得出数学结论的过程,进一步培养学生猜想经验,激发学生探索知识的兴趣.
【自主预习】
1.相似三角形已经学过哪些判定方法
2.说说如果两个三角形的三组对应边的比相等,那么这两个三角形相似与全等三角形条件SSS的区别与联系是什么
3.类比全等三角形条件SAS,如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似吗
如下图,若满足以下条件:
,∠A=∠A',那么△ABC与△A'B'C'相似吗
1.两边成比例且__________相等的两个三角形相似.
2.如图,已知△ABC,则下列四个三角形中,与△ABC相似的是( )
【合作探究】
活动1 探索新知
1.自主学习教材P33~34页,并完成自主预习区.
2.探索发现。
①在练习本上利用刻度尺和量角器画△ABC与△A'B'C',满足以下条件:=k (给定的值)和∠A=∠A'.量出它们的第三组对应边BC与B'C'的长,它们的比等于是吗 另外两组对应角分别相等吗
②改变∠A或是值的大小,再用同样的方法试一试,是否有同样的结论
3.得出结论:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
4.尝试证明(类似于判定1)
先作一个与△ABC全等的三角形,再证明它与△A'B'C'相似.
活动2 类比探索
对于△ABC和△A'B'C',,∠B=∠B',这两个三角形一定相似吗
小组讨论、交流.
教师点评:类似于全等中“SSA”一样不能作为三角形相似的判定方法.
【当堂反馈】
教材P34练习1①
知识点一 两边成比例且夹角相等的两个三角形相似
1.如图,线段AC与BD相交于O点,且OA=12,OC=54,OB=18,OD=36,则△ABO与△DCO__________(选填“一定”或“不”)相似.
第1题图 第2题图
2.如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
A.①和②相似 B.①和③相似 C.①和④相似 D.②和④相似
3.能判定AABC和△A'B'C'相似的条件是( )
A.,且∠B=∠B' B.,且∠A=∠C'
C.,且∠B=∠A' D.,且∠A=∠B'
4.如图,要使△ACD与△BCA相似,下列等式一定成立的是( )
A. B. C.CD2=AD·DB D.AC2=AD·AE
第4题图 第5题图 第6题图
知识点二 相似三角形判定的应用
5.如图,在△ABC中,点D、E两点分别在AB、AC上,且AD=5,BD=3,AE=4,EC=6,若∠A=40°,则图中∠1、∠2、∠3的大小关系正确的是( )
A.∠1>∠3 B.∠2=∠4 C.∠1>∠4 D.∠2=∠3
6.如图,在△ABC中,点D、E分别为AB、AC边上的点,.若AD=3,AC=5,DE=4,则BC=_______.
7.如图,BD平分∠ABC,AB=4,BC=6,当BD=_______时,△ABD∽△DBC.
【拓展提升】
1.如图所示,么DAB=么CAE,且AB·AD=AE·AC,问图中有与∠ADE相等的角吗 若有,请找出来,并说明理由.
2.如图所示,在△ABC中,AB=8cm,BC=16cm,点P从A开始沿AB边向点B以2cm/s的速度运动,点Q从点B开始沿BC边向点C以4cm/s的速度运动.如果P、Q分别从A、B同时出发,问经过几秒,以P、Q、B为顶点的三角形与△ABC相似
【课后检测】
一、选择题
1.D是△ABC的边AB上一点,要使△ACD∽△ABC,则它们必须具备的条件是( )
A. B. C.CD2=AD·DB D.AC2=AD·AB
第1题图 第2题图
2.如图,在正△ABC中,D、E分别在AC、AB上,且,AE=BE,则有( )
A.△AED∽△BED B.△AED∽△CBD
C.△AED∽△ABD D.△BAD∽△BCD
二、填空题
3.已知直线与x轴交于点A,与y轴交于点B,在x轴上有一点C,使B,O,C三点构成的三角形与△AOB相似,则点C的坐标为__________.
第3题图 第4题图
4.如图,在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,使△ADE与△ABC相似,则AE=__________.
三、解答题
5.如图,点D在△ABC内,连接AD、BD,将△ABD绕点A逆时针旋转得到△ACE,连接DE,试问:△ABC与△ADE相似吗 请说明理由.
6.如图,网格中的每个小正方形的边长都是l,每个小正方形的顶点叫做格点.△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
求证:(1)△ACB∽△DCE;
(2)EF⊥AB.
7.如图,D是△ABC的边BC上的一点,AB=2,BD=1,DC=3.
求证:△ABD∽△CBA.
编号:2705 班级: 姓名:
课题:两边成比例且夹角相等的两个三角形相似
主备: 审核: 时间: 年 月 日
【明确目标】
1.掌握判定两个三角形相似的方法:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
2.培养学生的观察、发现、比较、归纳能力,感受两个三角形相似的判定方法2与全等三角形判定方法(SAS)的区别与联系,体验事物间特殊与一般的关系.
3.经历两个三角形相似的探索过程,体验分析归纳得出数学结论的过程,进一步培养学生猜想经验,激发学生探索知识的兴趣.
【自主预习】
1.相似三角形已经学过哪些判定方法
2.说说如果两个三角形的三组对应边的比相等,那么这两个三角形相似与全等三角形条件SSS的区别与联系是什么
3.类比全等三角形条件SAS,如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似吗
如下图,若满足以下条件:
,∠A=∠A',那么△ABC与△A'B'C'相似吗
1.两边成比例且__________相等的两个三角形相似.
2.如图,已知△ABC,则下列四个三角形中,与△ABC相似的是( )
【合作探究】
活动1 探索新知
1.自主学习教材P33~34页,并完成自主预习区.
2.探索发现。
①在练习本上利用刻度尺和量角器画△ABC与△A'B'C',满足以下条件:=k (给定的值)和∠A=∠A'.量出它们的第三组对应边BC与B'C'的长,它们的比等于是吗 另外两组对应角分别相等吗
②改变∠A或是值的大小,再用同样的方法试一试,是否有同样的结论
3.得出结论:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
4.尝试证明(类似于判定1)
先作一个与△ABC全等的三角形,再证明它与△A'B'C'相似.
活动2 类比探索
对于△ABC和△A'B'C',,∠B=∠B',这两个三角形一定相似吗
小组讨论、交流.
教师点评:类似于全等中“SSA”一样不能作为三角形相似的判定方法.
【当堂反馈】
教材P34练习1①
知识点一 两边成比例且夹角相等的两个三角形相似
1.如图,线段AC与BD相交于O点,且OA=12,OC=54,OB=18,OD=36,则△ABO与△DCO__________(选填“一定”或“不”)相似.
第1题图 第2题图
2.如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
A.①和②相似 B.①和③相似 C.①和④相似 D.②和④相似
3.能判定AABC和△A'B'C'相似的条件是( )
A.,且∠B=∠B' B.,且∠A=∠C'
C.,且∠B=∠A' D.,且∠A=∠B'
4.如图,要使△ACD与△BCA相似,下列等式一定成立的是( )
A. B. C.CD2=AD·DB D.AC2=AD·AE
第4题图 第5题图 第6题图
知识点二 相似三角形判定的应用
5.如图,在△ABC中,点D、E两点分别在AB、AC上,且AD=5,BD=3,AE=4,EC=6,若∠A=40°,则图中∠1、∠2、∠3的大小关系正确的是( )
A.∠1>∠3 B.∠2=∠4 C.∠1>∠4 D.∠2=∠3
6.如图,在△ABC中,点D、E分别为AB、AC边上的点,.若AD=3,AC=5,DE=4,则BC=_______.
7.如图,BD平分∠ABC,AB=4,BC=6,当BD=_______时,△ABD∽△DBC.
【拓展提升】
1.如图所示,么DAB=么CAE,且AB·AD=AE·AC,问图中有与∠ADE相等的角吗 若有,请找出来,并说明理由.
2.如图所示,在△ABC中,AB=8cm,BC=16cm,点P从A开始沿AB边向点B以2cm/s的速度运动,点Q从点B开始沿BC边向点C以4cm/s的速度运动.如果P、Q分别从A、B同时出发,问经过几秒,以P、Q、B为顶点的三角形与△ABC相似
【课后检测】
一、选择题
1.D是△ABC的边AB上一点,要使△ACD∽△ABC,则它们必须具备的条件是( )
A. B. C.CD2=AD·DB D.AC2=AD·AB
第1题图 第2题图
2.如图,在正△ABC中,D、E分别在AC、AB上,且,AE=BE,则有( )
A.△AED∽△BED B.△AED∽△CBD
C.△AED∽△ABD D.△BAD∽△BCD
二、填空题
3.已知直线与x轴交于点A,与y轴交于点B,在x轴上有一点C,使B,O,C三点构成的三角形与△AOB相似,则点C的坐标为__________.
第3题图 第4题图
4.如图,在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,使△ADE与△ABC相似,则AE=__________.
三、解答题
5.如图,点D在△ABC内,连接AD、BD,将△ABD绕点A逆时针旋转得到△ACE,连接DE,试问:△ABC与△ADE相似吗 请说明理由.
6.如图,网格中的每个小正方形的边长都是l,每个小正方形的顶点叫做格点.△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
求证:(1)△ACB∽△DCE;
(2)EF⊥AB.
7.如图,D是△ABC的边BC上的一点,AB=2,BD=1,DC=3.
求证:△ABD∽△CBA.
