两角分别相等的两个三角形相似学案
文档属性
| 名称 | 两角分别相等的两个三角形相似学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 281.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-30 21:06:05 | ||
图片预览

文档简介
“一·三·六”导学案——九年级数学(下)
编号:2706 班级: 姓名:
课题:两角分别相等的两个三角形相似
主备: 审核: 时间:年 月 日
【明确目标】
1.掌握相似三角形的判定方法3(有两个角对应相等的两个三角形相似)和直角三角形相似,并运用它们解决一些实际问题.
2.经历探究相似三角形的判定,体会类比思想在学习数学中的作用.
3.在探究发现相似三角形的判定和直角三角形相似的过程中,体会动手操作的乐趣.
【自主预习】
判定三角形相似已有哪些定理 两个角相等的两个三角形相似吗 你有什么样的例子
阅读教材P35~36,自学“思考”及“例2”,理解相似三角形判定定理3及直角三角形相似的判定方法.
并思考解答下列问题.
①如果一个三角形的两个角与另一个三角形的两个角对应__________,那么这两个三角形相似.
②如果两个直角三角形中,有一-条直角边和斜边对应成比例,那么这两个直角三角形__________.
③要判定两个直角三角形相似,最简单的方法就是再找__________对应相等,就可以根据相似三角形的判定3,判定这两个直角三角形相似.
④如图所示,已知∠ADE=∠B,则△AED∽△_______.理由是____________________________________.
⑤顶角对应相等的两个等腰三角形相似吗 为什么
相似.理由:对应角相等的两个三角形相似.
教师点拨:要根据已知条件选择适当的方法.
1.两角分别__________的两个三角形相似.
2.斜边和一条直角边__________的两个直角三角形相似.
3.如图,在△ABC和△A'B'C'中,若∠A=60°,∠B=40°,∠A'=60°,当∠C'=_______时,则△ABC∽△A'B'C'.
4.在△ABC和△A'B'C'中,∠C=∠C'=90°,AC=3,AB=5,A'C'=6,则当A'B'=_______时,△ABC∽△A'B'C'.
【合作探究】
活动1 小组讨论(新知运用)
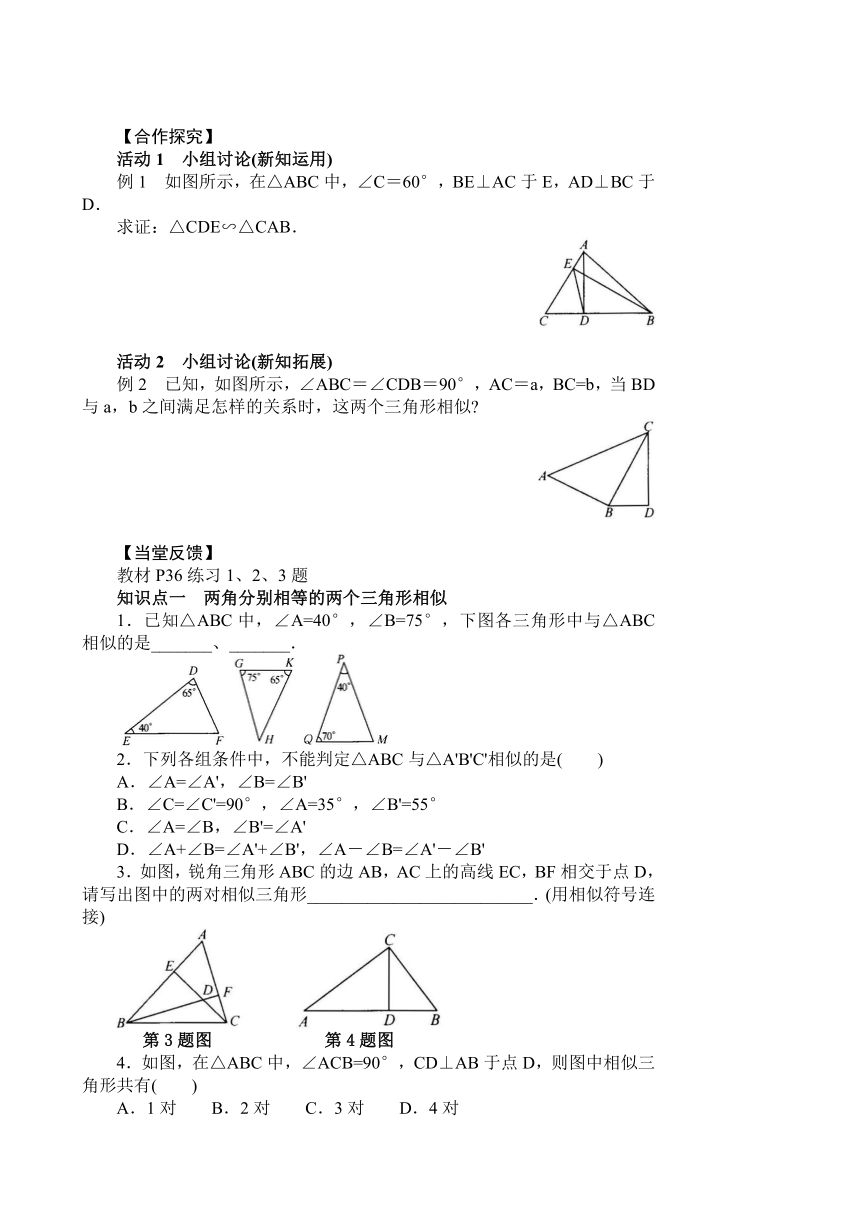
例1 如图所示,在△ABC中,∠C=60°,BE⊥AC于E,AD⊥BC于D.
求证:△CDE∽△CAB.
活动2 小组讨论(新知拓展)
例2 已知,如图所示,∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a,b之间满足怎样的关系时,这两个三角形相似
【当堂反馈】
教材P36练习1、2、3题
知识点一 两角分别相等的两个三角形相似
1.已知△ABC中,∠A=40°,∠B=75°,下图各三角形中与△ABC相似的是_______、_______.
2.下列各组条件中,不能判定△ABC与△A'B'C'相似的是( )
A.∠A=∠A',∠B=∠B'
B.∠C=∠C'=90°,∠A=35°,∠B'=55°
C.∠A=∠B,∠B'=∠A'
D.∠A+∠B=∠A'+∠B',∠A-∠B=∠A'-∠B'
3.如图,锐角三角形ABC的边AB,AC上的高线EC,BF相交于点D,请写出图中的两对相似三角形__________________________.(用相似符号连接)
第3题图 第4题图
4.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
知识点二 斜边和一直角边成比例的两个直角三角形相似
5.已知Rt△ABC中,∠C=90°,AB=15cm,BC=8cm,另一个Rt△DEF中,∠D=90°,EF=cm,DE一6cm,则△ABC与△DEF_______(选填“是”或“不是”)相似的两个三角形.
6.如图,在矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF等于( )
A. B.1 C. D.2
7.如图,△ABC中,AC=8cm,BC=6cm,AB=10cm.D是AB上一点,AD=4cm,DE⊥AB交AC于点E.当AE的长为多少时,△ADE与△ABC相似?
【拓展提升】
(1)如图所示,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.
①求证:△BCF≌△DCE;②若BC=5,CF=3,∠BFC=90°,求DG:GC的值.
(2)如图所示,在⊙O中,AB=AC,则△ABD∽_______,若AC=12,AE=8,则AD=_______.
第1题图 第2题图 第3题图
(3)如图所示,在直角坐标系中,有两点A(4,0),B(0,2),如果点C在x轴上(C与A不重合),使得由点B、O、C组成的三角形与△AOB相似,符合条件的C点的坐标为_______.
【课后检测】
一、选择题
1.如图,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;@AC2=AB·AD.其中单独能够判定△ABC∽△ACD的个数为( )
A.1个 B.2个 C.3个 D.4个
第1题图 第2题图 第3题图
2.如图,直角梯形ABCD中,AB∥CD,∠C=90°,∠BDA=90°,AB=a,BD=b,CD=c,BC=d,AD=e,则下列等式成立的是( )
A.b2=ac B.b2=ce C.be=ac D.bd=ae
二、填空题
3.已知∠ACB=∠ABD=90°,AB=,AC=2,当AD=__________时,△ABD与△BCA相似.
4.在△ABC中,AB>BC>AC,D是AC的中点,过点D作直线l,使截得的三角形与原三角形相似,这样的直线l有_______条.
三、解答题
5.如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.
6.已知:∠ACB=∠ABD=90°,AB=,AC=2,求AD的长为多少时,图中两直角三角形相似
7.如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
编号:2706 班级: 姓名:
课题:两角分别相等的两个三角形相似
主备: 审核: 时间:年 月 日
【明确目标】
1.掌握相似三角形的判定方法3(有两个角对应相等的两个三角形相似)和直角三角形相似,并运用它们解决一些实际问题.
2.经历探究相似三角形的判定,体会类比思想在学习数学中的作用.
3.在探究发现相似三角形的判定和直角三角形相似的过程中,体会动手操作的乐趣.
【自主预习】
判定三角形相似已有哪些定理 两个角相等的两个三角形相似吗 你有什么样的例子
阅读教材P35~36,自学“思考”及“例2”,理解相似三角形判定定理3及直角三角形相似的判定方法.
并思考解答下列问题.
①如果一个三角形的两个角与另一个三角形的两个角对应__________,那么这两个三角形相似.
②如果两个直角三角形中,有一-条直角边和斜边对应成比例,那么这两个直角三角形__________.
③要判定两个直角三角形相似,最简单的方法就是再找__________对应相等,就可以根据相似三角形的判定3,判定这两个直角三角形相似.
④如图所示,已知∠ADE=∠B,则△AED∽△_______.理由是____________________________________.
⑤顶角对应相等的两个等腰三角形相似吗 为什么
相似.理由:对应角相等的两个三角形相似.
教师点拨:要根据已知条件选择适当的方法.
1.两角分别__________的两个三角形相似.
2.斜边和一条直角边__________的两个直角三角形相似.
3.如图,在△ABC和△A'B'C'中,若∠A=60°,∠B=40°,∠A'=60°,当∠C'=_______时,则△ABC∽△A'B'C'.
4.在△ABC和△A'B'C'中,∠C=∠C'=90°,AC=3,AB=5,A'C'=6,则当A'B'=_______时,△ABC∽△A'B'C'.
【合作探究】
活动1 小组讨论(新知运用)
例1 如图所示,在△ABC中,∠C=60°,BE⊥AC于E,AD⊥BC于D.
求证:△CDE∽△CAB.
活动2 小组讨论(新知拓展)
例2 已知,如图所示,∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a,b之间满足怎样的关系时,这两个三角形相似
【当堂反馈】
教材P36练习1、2、3题
知识点一 两角分别相等的两个三角形相似
1.已知△ABC中,∠A=40°,∠B=75°,下图各三角形中与△ABC相似的是_______、_______.
2.下列各组条件中,不能判定△ABC与△A'B'C'相似的是( )
A.∠A=∠A',∠B=∠B'
B.∠C=∠C'=90°,∠A=35°,∠B'=55°
C.∠A=∠B,∠B'=∠A'
D.∠A+∠B=∠A'+∠B',∠A-∠B=∠A'-∠B'
3.如图,锐角三角形ABC的边AB,AC上的高线EC,BF相交于点D,请写出图中的两对相似三角形__________________________.(用相似符号连接)
第3题图 第4题图
4.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
知识点二 斜边和一直角边成比例的两个直角三角形相似
5.已知Rt△ABC中,∠C=90°,AB=15cm,BC=8cm,另一个Rt△DEF中,∠D=90°,EF=cm,DE一6cm,则△ABC与△DEF_______(选填“是”或“不是”)相似的两个三角形.
6.如图,在矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF等于( )
A. B.1 C. D.2
7.如图,△ABC中,AC=8cm,BC=6cm,AB=10cm.D是AB上一点,AD=4cm,DE⊥AB交AC于点E.当AE的长为多少时,△ADE与△ABC相似?
【拓展提升】
(1)如图所示,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.
①求证:△BCF≌△DCE;②若BC=5,CF=3,∠BFC=90°,求DG:GC的值.
(2)如图所示,在⊙O中,AB=AC,则△ABD∽_______,若AC=12,AE=8,则AD=_______.
第1题图 第2题图 第3题图
(3)如图所示,在直角坐标系中,有两点A(4,0),B(0,2),如果点C在x轴上(C与A不重合),使得由点B、O、C组成的三角形与△AOB相似,符合条件的C点的坐标为_______.
【课后检测】
一、选择题
1.如图,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;@AC2=AB·AD.其中单独能够判定△ABC∽△ACD的个数为( )
A.1个 B.2个 C.3个 D.4个
第1题图 第2题图 第3题图
2.如图,直角梯形ABCD中,AB∥CD,∠C=90°,∠BDA=90°,AB=a,BD=b,CD=c,BC=d,AD=e,则下列等式成立的是( )
A.b2=ac B.b2=ce C.be=ac D.bd=ae
二、填空题
3.已知∠ACB=∠ABD=90°,AB=,AC=2,当AD=__________时,△ABD与△BCA相似.
4.在△ABC中,AB>BC>AC,D是AC的中点,过点D作直线l,使截得的三角形与原三角形相似,这样的直线l有_______条.
三、解答题
5.如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.
6.已知:∠ACB=∠ABD=90°,AB=,AC=2,求AD的长为多少时,图中两直角三角形相似
7.如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
