二元一次方程与一次函数

6.二元一次方程和一次函数
●教学时间
第七课时
●课 题
§7.6 二元一次方程和一次函数
●教学目标
(一)教学知识点
1.二元一次方程和一次函数的关系.
2.二元一次方程组的图象解法.
(二)能力训练要求
1.使学生初步理解二元一次方程与一次函数的关系.
2.通过学生的思考和操作，在力图提示出方程与图象之间的关系，引入二元一次方程组的图象解法.同时培养了学生初步的数形结合的意识和能力.
(三)情感与价值观要求
通过学生的自主探索，提示出方程和图象之间的对应关系，加强了新旧知识的联系，培养了学生的创新意识，激发了学生学习数学的兴趣.
●教学重点
1.二元一次方程和一次函数的关系.
2.能根据一次函数的图象求二元一次方程组的近似解.
●教学难点
方程和函数之间的对应关系即数形结合的意识和能力.
●教学方法
学生操作——自主探索的方法.
学生通过自己操作和思考，结合新旧知识的联系，自主探索出方程与图象之间的对应关系，以引入二元一次方程组的图象解法，同时也建立了“数”——二元一次方程组与“形”——函数的图象(直线)之间的对应关系，培养了学生数形结合的意识和能力.
●教具准备
投影片两张：
第一张：问题串(记作§7.6 A)；
第二张：补充练习(记作§7.6 B).
●教学过程
Ⅰ.回忆旧知识，引入新课
［师］举例说明什么是二元一次方程？什么是二元一次方程的解？二元一次方程的解的个数如何？为什么？
［生］例如x+y=8含有两个未知数x,y且未知数的项的次数是一次，所以x+y=8是二元一次方程.
是适合方程x+y=8的一组未知数的值，所以是二元一次方程x+y=8的一个解.
我们不难发现适合x+y=8的一组未知数的值不只再例如;;……都适合方程x+y=8，所以说它们都是x+y=8的解.x+y=8有无数多个解，只要给出一个x的值，代入x+y=8中，就可得到一个y的值.这样一组一组的未知数的值都是x+y=8的解.
［师］如果将方程x+y=8利用等式的性质变形，就可得到y=8－x，同学们能联想到什么？
［生］y=8－x是一个一次函数，x、y在一次函数中不是未知数，而是两个变量，x是自变量，y是因变量.
［师］这位同学回答得很好，他能够把所学的知识联系起来，这正是我们学习数学最可贵的地方之一.我们说到函数，不得不想到函数的图象，因为函数的图象可直观地反映出y随x变化的情况.那么函数的图象如何画出来的呢？
［生］我们知道在函数中，给出自变量x的值，就对应着一个y的值.我们把x的值作为点的横坐标，对应的y的值作为这个点的纵坐标.在直角坐标系中描出它的对应点，所有这些点组成的图形叫做该函数的图象.
［师］下面就请同学们画出一次函数y=8－x的图象.
我们观察y=8－x的图象可知：
(1)满足关系式y=8－x的x、y所对应的点(x,y)都在一次函数y=8－x的图象上.
(2)一次函数y=8－x的图象上的点(x,y)都满足关系式y=8－x.
(3)满足关系式y=8－x的x、y的值恰好就是二元一次方程x+y=8的解.
因此我们猜想二元一次方程的解与相应的一次函数图象上的点有无对应关系呢？
这节课我们主要就来研究二元一次方程与一次函数的关系.
Ⅱ.讲授讲课
出示投影片(§7.6 A)
(1)方程x+y=5的解有多少个？写出其中几个？(2)在直角坐标系中分别描出以这些解为坐标的点，它们在一次函数y=5－x的图象上吗？(3)在一次函数y=5－x的图象上任取一点，它的坐标适合方程x+y=5吗？(4)以方程x+y=5的解为坐标的所有点组成的图象与一次函数y=5－x的图象相同吗？
［师］对于以上几个问题分组讨论，并归纳出二元一次方程和一次函数的关系.
［生］(1)方程x+y=5的解有无数个.例如……
(2)我们不妨先画出y=5－x的图象.
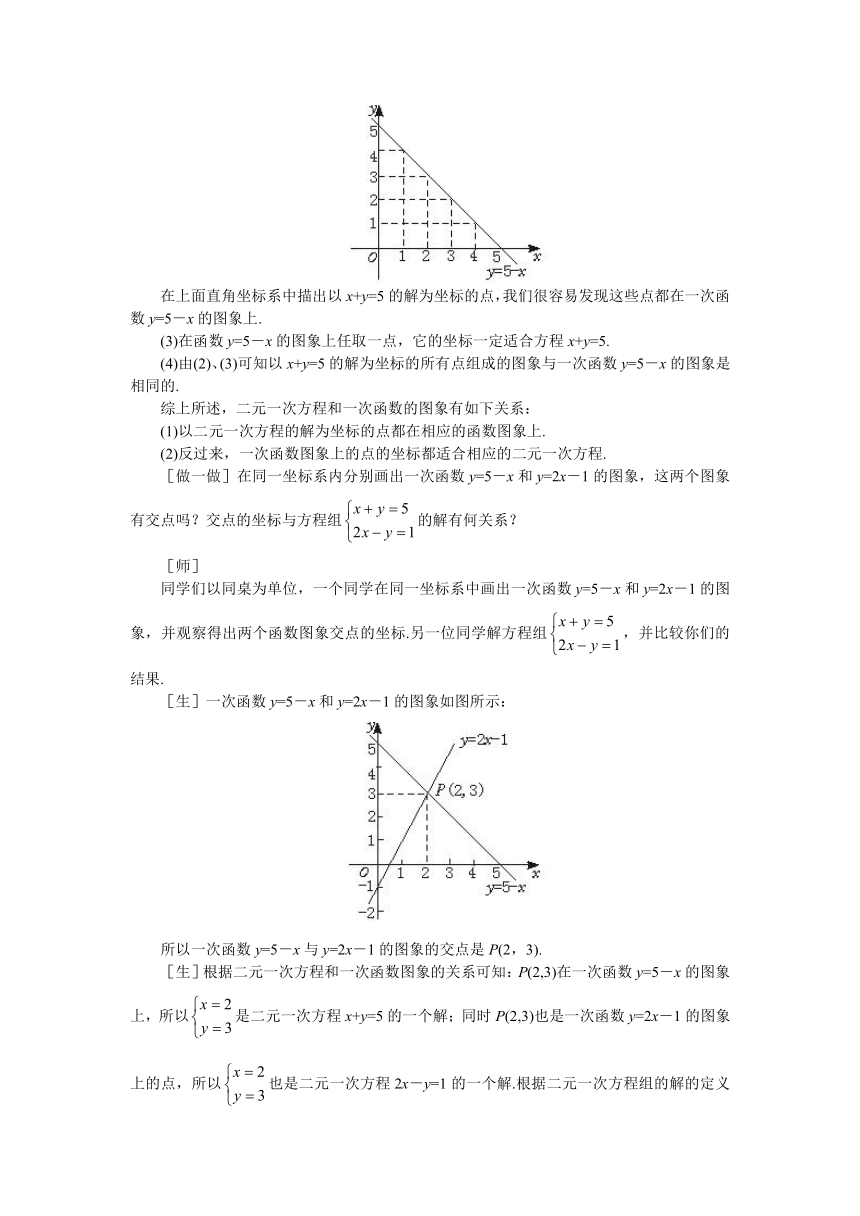
在上面直角坐标系中描出以x+y=5的解为坐标的点，我们很容易发现这些点都在一次函数y=5－x的图象上.
(3)在函数y=5－x的图象上任取一点，它的坐标一定适合方程x+y=5.
(4)由(2)、(3)可知以x+y=5的解为坐标的所有点组成的图象与一次函数y=5－x的图象是相同的.
综上所述，二元一次方程和一次函数的图象有如下关系：
(1)以二元一次方程的解为坐标的点都在相应的函数图象上.
(2)反过来，一次函数图象上的点的坐标都适合相应的二元一次方程.
［做一做］在同一坐标系内分别画出一次函数y=5－x和y=2x－1的图象，这两个图象有交点吗？交点的坐标与方程组的解有何关系？
［师］
同学们以同桌为单位，一个同学在同一坐标系中画出一次函数y=5－x和y=2x－1的图象，并观察得出两个函数图象交点的坐标.另一位同学解方程组，并比较你们的结果.
［生］一次函数y=5－x和y=2x－1的图象如图所示：
所以一次函数y=5－x与y=2x－1的图象的交点是P(2，3).
［生］根据二元一次方程和一次函数图象的关系可知：P(2,3)在一次函数y=5－x的图象上，所以是二元一次方程x+y=5的一个解；同时P(2,3)也是一次函数y=2x－1的图象上的点，所以也是二元一次方程2x－y=1的一个解.根据二元一次方程组的解的定义可知是的解.
［生］老师，用消元法解二元一次方程组得到的解也是.
［师］因此，我们又有了解二元一次方程组的新的方法——图象法.下面我们来看一个例题.
［例1］用作图象的方法解方程得
分析：在同一坐标中作出相应的两个一次函数的图象.观察图象的交点便可得出方程的解.
解：由x－2y=－2可得y=x+1,
同理，由2x－y=2可得y=2x－2,
在同一坐标系内作出一次函数y=x+1的图象l1和y=2x－2的图象l2.如下图.
观察图象，得l1,l2的交点为P(2，2).
所以方程组的解是
Ⅲ.随堂练习
1.课本P208.
(1)用作图解的方法解方程组.
解：由2x+y=4得y=4－2x
同理，由2x－3y=12得y=x－4,
在同一坐标系中作函数y=4－2x的图象l1和函数y=x－4的图象l2,如下图所示：
观察图象，得l1,l2的交点P(3，－2)
所以方程组的解为
(2)下图中的两直线l1,l2的交点坐标可以看作方程组_________的解.
解：由图象可知l1过点(1，3)、(0，1).设l1是函数y=k1x+b1的图象，根据题意，得
解得k1=2,b1=1.
所以l1是函数y=2x+1的图象.
l1同理可得l2是函数y=4－x的图象.所以l1、l2交点的坐标可看做二元一次方程组的解.
2.补充练习(出示投影片§7.6 B)
如图，l甲，l乙分别表示甲走路与乙骑自行车(在同一条路上)行走的路程s与时间t的关系观察图象并回答下列问题：
(1)乙出发时，与甲相距_________千米；(2)走了一段路程后，乙的自行车发生故障，停下来修理，修车的时间为[CD#2]时；(3)乙从出发起，经过_________时与甲相遇；(4)甲行走的路程s(千米)与时间t(时)之间的函数关系式是_________.(5)如果乙的自行车不出现故障，那么乙出发后经过_________时与甲相遇，相遇处离乙的出发点_________千米，并在图中标出其相遇点.
解：由图示得：
(1)10千米 (2)1小时 (3)3小时
(4)设甲行走的路程s与时间t之间的函数关系为S=kt+b(t≥0).由于此函数的图象过(0，10)和(3，22.5)，根据题意可得b=10，k=.所以甲行走的路程s与时间t之间的函数关系为s=t+10(t≥0)
(5)如果乙不出现故障，乙行走的路程s与t之间的函数关系式为s=15t(t≥0).在同一坐标系中画出甲走路和乙骑自行车行走的路程s与时间t的关系，如下图：
由图可知乙出发后经过小时与甲相遇，相遇时离乙的出发点为≈13.9千米.相遇点为图中P(，)点.
Ⅳ.课时小结
本节课我们通过操作和思考，揭示了二元一次方程和函数图象之间的对应关系，从而引出了二元一次方程组的图象解法，同时也建立了“数”——二元一次方程组与“形”——函数图象之间的对应关系，培养了学生初步的数形结合的意识和能力.其实，在我们平时解二元一次方程组时，大多还用的消元法.但对于我们将来要学习的高次方程、无理方程等的求解，画图象的方法更具一般性.无疑这节的学习为我们的后继学习打下了基础.因此这节课用图象法求二元一次方程组的解必须理解和掌握.
Ⅴ.课后作业
1.课本P208、习题7.7.
2.收集有关科学家和方程的故事.
Ⅵ.活动与挖究
有一组数同时适合方程x+y=2和x+y=5吗？一次函数y=2－x，y=5－x的图象之间有何关系？你能从中“悟”出些什么？
过程：学生经过尝试是很容易发现x+y=2和x+y=5时没有一组数同时适合这两个二元一次方程的.即这个二元一次方程组无解.
对于一次函数y=2－x，y=5－x的图象可以让学生作出它们的图象(下图)观察可以发现它们的图象(直线)是互相平行的，即它们无公共点.
结果：我们从中可以“悟”出：方程组的解与函数图象交点之间的关系：当函数的图象有交点时，说明相应的二元一次方程组有解；当函数的图象(直线)平行即无交点时，说明相应的二元一次方程组无解.反之也成立.
●板书设计
§7.6 二元一次方程和一次函数一、二元一次方程和一次函数的关系(1)以二元一次方程的解为坐标的点在相应的一次函数图象上.(2)一次函数图象上的点的坐标是相应的二元一次方程的解.二、用图象法解二元一次方程组［做一做］［例题］三、随堂练习(学生板演)四、课时小结