人教版数学九年级下册 第二十六章反比例函数 单元测试(含答案)
文档属性
| 名称 | 人教版数学九年级下册 第二十六章反比例函数 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 144.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 08:44:13 | ||
图片预览

文档简介
人教九年级下 单元测试
第26章
班级________ 姓名________
一、选择题(本大题共10小题,共30分)
下列关系式中,不是y关于x的反比例函数的是( )
A. B. C. D.
反比例函数y=(2m+1),当x>0时,y随x的增大而增大,则m的值是( )
A. B. 小于的实数 C. D.
下列函数中,经过一,三象限的反比例函数是( )
A. B. C. D.
如图,A为反比例函数y=图象上的一点,AB⊥y轴于B,点P在x轴上,S△ABP=2,则这个反比例函数的表达式为( )
A. B.
C. D.
如果A (2,y1),B(-3,y2)两点都在反比例函数y=的图象上,那么y1与y2的大小关系是( )
A. B. C. D.
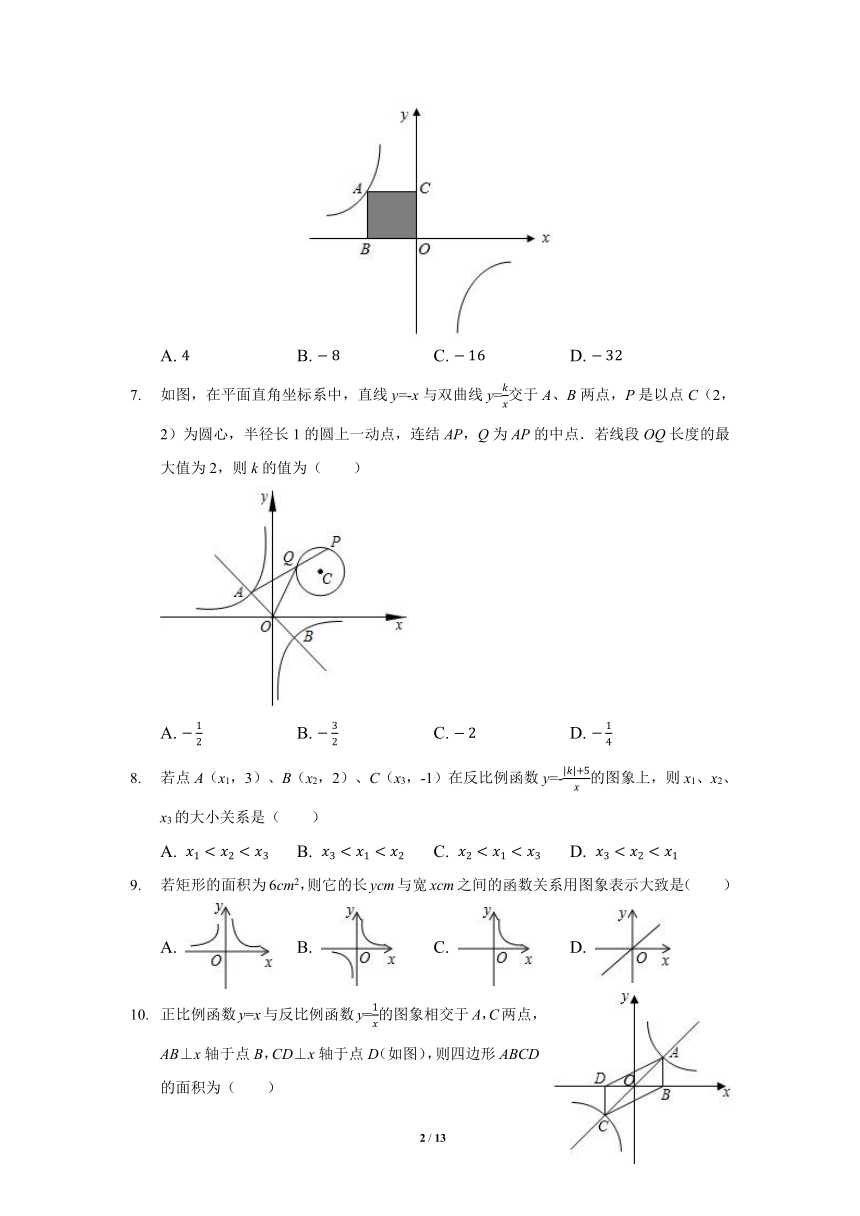
如图,点A是反比例函数y=图象上的一个动点,点A作AB⊥x轴;AC⊥y轴,垂足分别为B,C,矩形ABOC的面积为16,则k=( )
A. B. C. D.
如图,在平面直角坐标系中,直线y=-x与双曲线y=交于A、B两点,P是以点C(2,2)为圆心,半径长1的圆上一动点,连结AP,Q为AP的中点.若线段OQ长度的最大值为2,则k的值为( )
A. B. C. D.
若点A(x1,3)、B(x2,2)、C(x3,-1)在反比例函数y=-的图象上,则x1、x2、x3的大小关系是( )
A. B. C. D.
若矩形的面积为6cm2,则它的长ycm与宽xcm之间的函数关系用图象表示大致是( )
A. B. C. D.
正比例函数y=x与反比例函数y=的图象相交于A,C两点,AB⊥x轴于点B,CD⊥x轴于点D(如图),则四边形ABCD的面积为( )
A. B. C. D.
二、填空题(本大题共10小题,共30分)
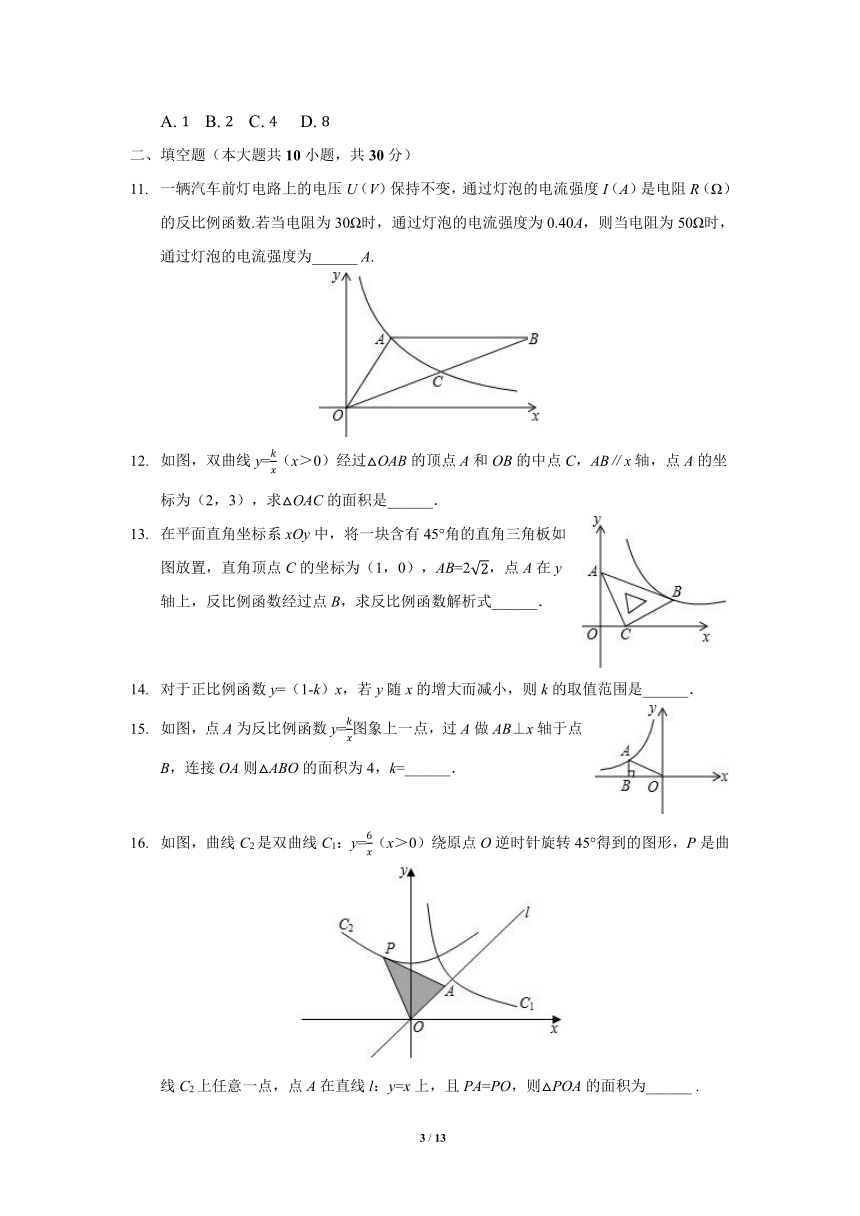
一辆汽车前灯电路上的电压U(V)保持不变,通过灯泡的电流强度I(A)是电阻R(Ω)的反比例函数.若当电阻为30Ω时,通过灯泡的电流强度为0.40A,则当电阻为50Ω时,通过灯泡的电流强度为______ A.
如图,双曲线y=(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),求△OAC的面积是______.
在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),AB=2,点A在y轴上,反比例函数经过点B,求反比例函数解析式______.
对于正比例函数y=(1-k)x,若y随x的增大而减小,则k的取值范围是______.
如图,点A为反比例函数y=图象上一点,过A做AB⊥x轴于点B,连接OA则△ABO的面积为4,k=______.
如图,曲线C2是双曲线C1:y=(x>0)绕原点O逆时针旋转45°得到的图形,P是曲线C2上任意一点,点A在直线l:y=x上,且PA=PO,则△POA的面积为______ .
阅读理解:对于任意正实数a,b,
∵(-)2≥0,
∴ a-2+b≥0,
∴ a+b≥2,只有当a=b时,等号成立.
结论:在 a+b≥2(a,b均为正实数)中,若ab为定值P,则a+b≥2,
当 a=b,a+b有最小值2.
根据上述内容,回答下列问题:
(1)若x>0,x+的最小值为 .
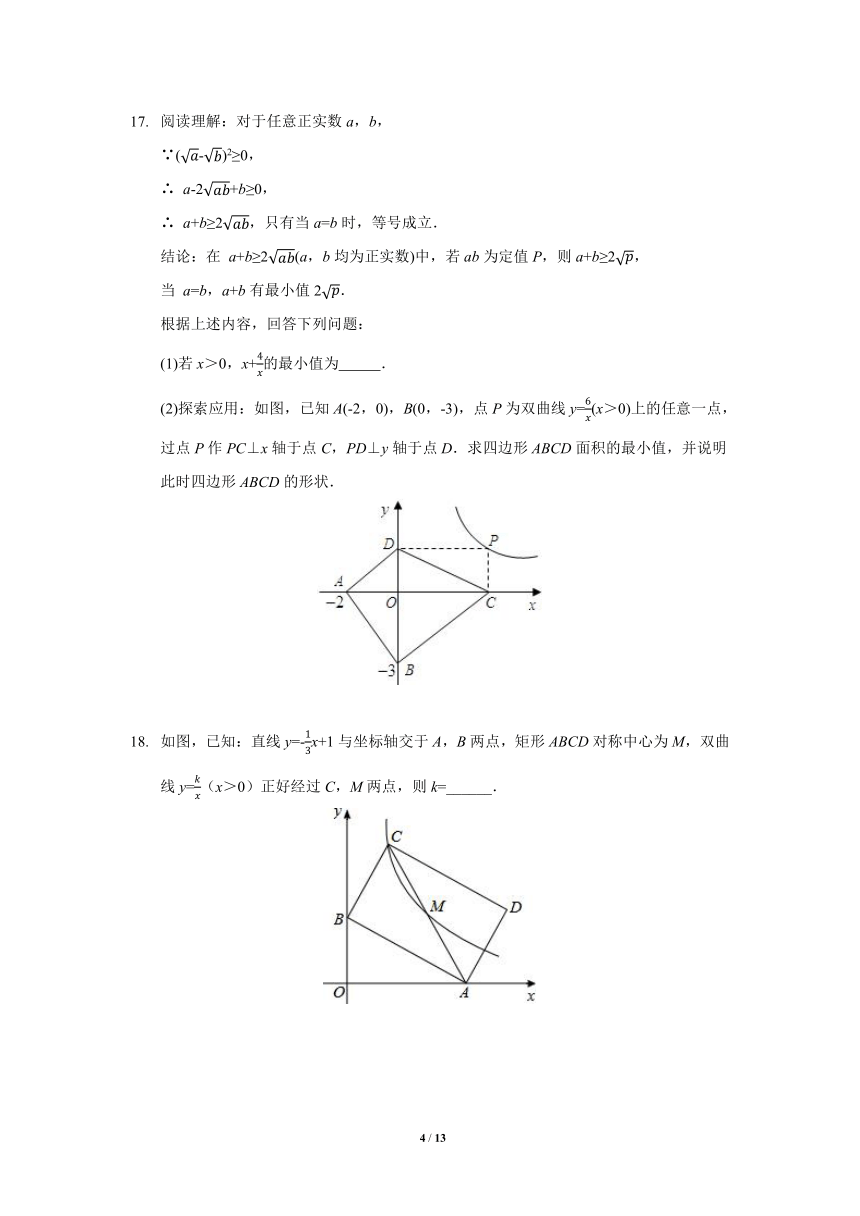
(2)探索应用:如图,已知A(-2,0),B(0,-3),点P为双曲线y=(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
如图,已知:直线y=-x+1与坐标轴交于A,B两点,矩形ABCD对称中心为M,双曲线y=(x>0)正好经过C,M两点,则k=______.
如图, ABCD的顶点A在反比例函数y=-的图象上,顶点B在x轴的正半轴上,顶点C和D在反比例函数y=的图象上,且对角线AC∥x轴,则平行四边形ABCD的面积等于______.
如图,将平行四边形ABCD沿EF对折,使点A落在点C处,若∠A=60°,AD=6,AB=12,则AE的长为______.
三、计算题(本大题共1小题,共6分)
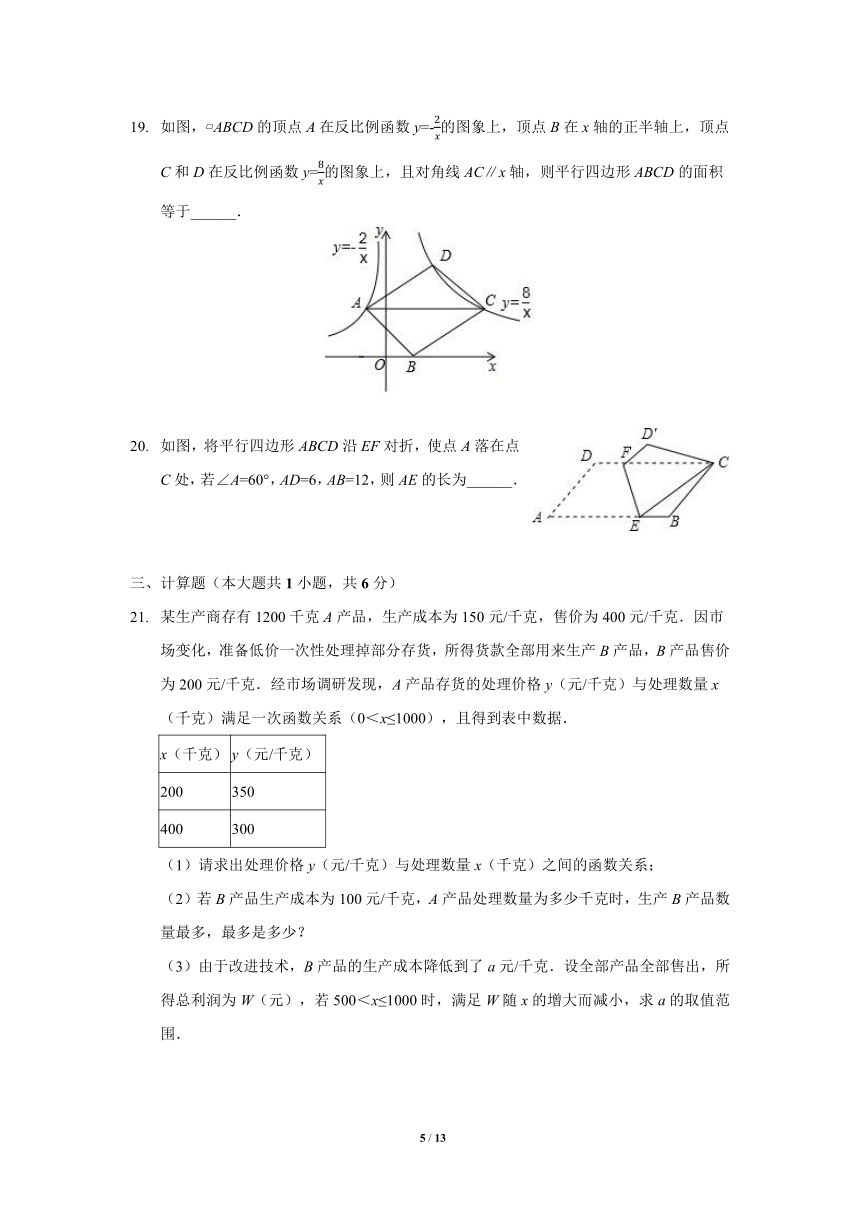
某生产商存有1200千克A产品,生产成本为150元/千克,售价为400元/千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产B产品,B产品售价为200元/千克.经市场调研发现,A产品存货的处理价格y(元/千克)与处理数量x(千克)满足一次函数关系(0<x≤1000),且得到表中数据.
x(千克) y(元/千克)
200 350
400 300
(1)请求出处理价格y(元/千克)与处理数量x(千克)之间的函数关系;
(2)若B产品生产成本为100元/千克,A产品处理数量为多少千克时,生产B产品数量最多,最多是多少?
(3)由于改进技术,B产品的生产成本降低到了a元/千克.设全部产品全部售出,所得总利润为W(元),若500<x≤1000时,满足W随x的增大而减小,求a的取值范围.
四、解答题(本大题共3小题,共34分)
(15分)如图是函数与函数在第一象限内的图象,点是的图象上一动点,轴于点A,交的图象于点,轴于点B,交的图象于点.
(1)求证:D是BP的中点;
(2)求出四边形ODPC的面积.
如图,双曲线y=(x>0)经过△OAB的顶点A和OB的三等分点C,且OC:OB=1:3,AB∥x轴,点A的坐标为(2,5)
(1)求k的值;
(2)求点C的坐标和△OAB的面积.
如图,已知正方形ABCD,∠MAN=45°,连接CB,交AM、AN分别于点P、Q,求证:CP2+BQ2=PQ2.
1.B
2.C
3.B
4.D
5.A
6.C
7.A
8.C
9.C
10.B
11.0.24
12.
13.
14.k>1
15.-8
16.6
17.解:(1)4;
(2)设P(x, ),则C(x,0),D(0, ),
∴四边形ABCD面积S= AC DB= ( x+2)( +3)
= ( x+ )+6,
由 (1)得若x>0,x+ 的最小值为 4,
∴四边形ABCD面积S≥ ×4+6=12,
∴四边形ABCD面积的最小值为12.
此时 x = ,则 x =2,
∴ C(2,0),D(0,3),
∴ OA=OC=2,OD=OB=3,
∴四边形ABCD是平行四边形.
又 AC ⊥BD,
∴四边形ABCD是菱形.
18.4
19.10
20.
21.解:(1)设y=kx+b,
根据题意,得:,
解得:,
∴y=-x+400(0<x≤1000);
(2)生产B产品的数量z==-x2+4x=-(x-800)2+1600,
∴当x=800时,生产B产品数量最多,最多为1600千克;
(3)W=400(1200-x)+200×-1200×150
=-x2+x+300000,
∴对称轴x==800-4a,
∵-<0,若500<x≤1000时,W随x的增大而减小,
则800-4a≤500,即a≥75,
∴a的取值范围是75≤a<100.
22.(1)证明:
∵点P在函数 上,
∴设P点坐标为( ,m),
∵点D在函数 上,BP∥ 轴,
∴设D点坐标为( ,m).
由题意可得 BD= ,BP= ,
故D是BP的中点.
(2)解:S四边形PBOA = ﹒
设C点坐标为( , ), D点坐标为( , ),
则S△OBD= = ,
S△OAC= = ,
∴S四边形ODPC=S四边形PBOA—S△OBD—S△OAC=6— — =3
(1)设P点的坐标为(a,b),设D点的坐标为(m,n),
∴点D为BP的中点
(2)
23.解:(1)将点A(2,5)代入解析式y=,
得:k=10;
(2)过点C作CN⊥y轴,垂足为N,延长BA,交y轴于点M,
∵AB∥x轴,
∴BM⊥y轴,
∴MB∥CN,
∴△OCN∽△OBM,
∵C为OB的三等分点,即=,
∴=()2=,==,
∴=,则ON=,即点C的纵坐标是.
∵A,C都在双曲线y=,点C的横坐标为:=6,故C(6,)
∴S△OCN=S△AOM=5,
由=,
得:S△AOB=40,
则△AOB面积为40.
24.证明:将△ABQ绕A点顺时针旋转90°得到△ACQ′,连接PQ′,
∴AQ′=AQ,CQ′=BQ,∠BAQ=∠CAQ′,∠ACQ′=∠ABC,
∵四边形ABCD为正方形,
∴∠ACQ′=∠ABC=∠ACB=45°,∠CAB=90°,
∵∠MAN=45°,
∴∠CAP+∠BAQ=45°,
∴∠Q′AP=∠CAQ′+∠CAP=45°,
∴∠Q′AP=∠QAP,
在△Q′AP和△QAP中,
,
∴△Q′AP≌△QAP(SAS),
∴PQ=PQ′,
∵∠Q′CP=∠ACQ′+∠ACB=90°,
在Rt△Q′CP中,由勾股定理得,
Q′P2=Q′C2+CP2,
∴CP2+BQ2=PQ2.
1 / 13
第26章
班级________ 姓名________
一、选择题(本大题共10小题,共30分)
下列关系式中,不是y关于x的反比例函数的是( )
A. B. C. D.
反比例函数y=(2m+1),当x>0时,y随x的增大而增大,则m的值是( )
A. B. 小于的实数 C. D.
下列函数中,经过一,三象限的反比例函数是( )
A. B. C. D.
如图,A为反比例函数y=图象上的一点,AB⊥y轴于B,点P在x轴上,S△ABP=2,则这个反比例函数的表达式为( )
A. B.
C. D.
如果A (2,y1),B(-3,y2)两点都在反比例函数y=的图象上,那么y1与y2的大小关系是( )
A. B. C. D.
如图,点A是反比例函数y=图象上的一个动点,点A作AB⊥x轴;AC⊥y轴,垂足分别为B,C,矩形ABOC的面积为16,则k=( )
A. B. C. D.
如图,在平面直角坐标系中,直线y=-x与双曲线y=交于A、B两点,P是以点C(2,2)为圆心,半径长1的圆上一动点,连结AP,Q为AP的中点.若线段OQ长度的最大值为2,则k的值为( )
A. B. C. D.
若点A(x1,3)、B(x2,2)、C(x3,-1)在反比例函数y=-的图象上,则x1、x2、x3的大小关系是( )
A. B. C. D.
若矩形的面积为6cm2,则它的长ycm与宽xcm之间的函数关系用图象表示大致是( )
A. B. C. D.
正比例函数y=x与反比例函数y=的图象相交于A,C两点,AB⊥x轴于点B,CD⊥x轴于点D(如图),则四边形ABCD的面积为( )
A. B. C. D.
二、填空题(本大题共10小题,共30分)
一辆汽车前灯电路上的电压U(V)保持不变,通过灯泡的电流强度I(A)是电阻R(Ω)的反比例函数.若当电阻为30Ω时,通过灯泡的电流强度为0.40A,则当电阻为50Ω时,通过灯泡的电流强度为______ A.
如图,双曲线y=(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),求△OAC的面积是______.
在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),AB=2,点A在y轴上,反比例函数经过点B,求反比例函数解析式______.
对于正比例函数y=(1-k)x,若y随x的增大而减小,则k的取值范围是______.
如图,点A为反比例函数y=图象上一点,过A做AB⊥x轴于点B,连接OA则△ABO的面积为4,k=______.
如图,曲线C2是双曲线C1:y=(x>0)绕原点O逆时针旋转45°得到的图形,P是曲线C2上任意一点,点A在直线l:y=x上,且PA=PO,则△POA的面积为______ .
阅读理解:对于任意正实数a,b,
∵(-)2≥0,
∴ a-2+b≥0,
∴ a+b≥2,只有当a=b时,等号成立.
结论:在 a+b≥2(a,b均为正实数)中,若ab为定值P,则a+b≥2,
当 a=b,a+b有最小值2.
根据上述内容,回答下列问题:
(1)若x>0,x+的最小值为 .
(2)探索应用:如图,已知A(-2,0),B(0,-3),点P为双曲线y=(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
如图,已知:直线y=-x+1与坐标轴交于A,B两点,矩形ABCD对称中心为M,双曲线y=(x>0)正好经过C,M两点,则k=______.
如图, ABCD的顶点A在反比例函数y=-的图象上,顶点B在x轴的正半轴上,顶点C和D在反比例函数y=的图象上,且对角线AC∥x轴,则平行四边形ABCD的面积等于______.
如图,将平行四边形ABCD沿EF对折,使点A落在点C处,若∠A=60°,AD=6,AB=12,则AE的长为______.
三、计算题(本大题共1小题,共6分)
某生产商存有1200千克A产品,生产成本为150元/千克,售价为400元/千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产B产品,B产品售价为200元/千克.经市场调研发现,A产品存货的处理价格y(元/千克)与处理数量x(千克)满足一次函数关系(0<x≤1000),且得到表中数据.
x(千克) y(元/千克)
200 350
400 300
(1)请求出处理价格y(元/千克)与处理数量x(千克)之间的函数关系;
(2)若B产品生产成本为100元/千克,A产品处理数量为多少千克时,生产B产品数量最多,最多是多少?
(3)由于改进技术,B产品的生产成本降低到了a元/千克.设全部产品全部售出,所得总利润为W(元),若500<x≤1000时,满足W随x的增大而减小,求a的取值范围.
四、解答题(本大题共3小题,共34分)
(15分)如图是函数与函数在第一象限内的图象,点是的图象上一动点,轴于点A,交的图象于点,轴于点B,交的图象于点.
(1)求证:D是BP的中点;
(2)求出四边形ODPC的面积.
如图,双曲线y=(x>0)经过△OAB的顶点A和OB的三等分点C,且OC:OB=1:3,AB∥x轴,点A的坐标为(2,5)
(1)求k的值;
(2)求点C的坐标和△OAB的面积.
如图,已知正方形ABCD,∠MAN=45°,连接CB,交AM、AN分别于点P、Q,求证:CP2+BQ2=PQ2.
1.B
2.C
3.B
4.D
5.A
6.C
7.A
8.C
9.C
10.B
11.0.24
12.
13.
14.k>1
15.-8
16.6
17.解:(1)4;
(2)设P(x, ),则C(x,0),D(0, ),
∴四边形ABCD面积S= AC DB= ( x+2)( +3)
= ( x+ )+6,
由 (1)得若x>0,x+ 的最小值为 4,
∴四边形ABCD面积S≥ ×4+6=12,
∴四边形ABCD面积的最小值为12.
此时 x = ,则 x =2,
∴ C(2,0),D(0,3),
∴ OA=OC=2,OD=OB=3,
∴四边形ABCD是平行四边形.
又 AC ⊥BD,
∴四边形ABCD是菱形.
18.4
19.10
20.
21.解:(1)设y=kx+b,
根据题意,得:,
解得:,
∴y=-x+400(0<x≤1000);
(2)生产B产品的数量z==-x2+4x=-(x-800)2+1600,
∴当x=800时,生产B产品数量最多,最多为1600千克;
(3)W=400(1200-x)+200×-1200×150
=-x2+x+300000,
∴对称轴x==800-4a,
∵-<0,若500<x≤1000时,W随x的增大而减小,
则800-4a≤500,即a≥75,
∴a的取值范围是75≤a<100.
22.(1)证明:
∵点P在函数 上,
∴设P点坐标为( ,m),
∵点D在函数 上,BP∥ 轴,
∴设D点坐标为( ,m).
由题意可得 BD= ,BP= ,
故D是BP的中点.
(2)解:S四边形PBOA = ﹒
设C点坐标为( , ), D点坐标为( , ),
则S△OBD= = ,
S△OAC= = ,
∴S四边形ODPC=S四边形PBOA—S△OBD—S△OAC=6— — =3
(1)设P点的坐标为(a,b),设D点的坐标为(m,n),
∴点D为BP的中点
(2)
23.解:(1)将点A(2,5)代入解析式y=,
得:k=10;
(2)过点C作CN⊥y轴,垂足为N,延长BA,交y轴于点M,
∵AB∥x轴,
∴BM⊥y轴,
∴MB∥CN,
∴△OCN∽△OBM,
∵C为OB的三等分点,即=,
∴=()2=,==,
∴=,则ON=,即点C的纵坐标是.
∵A,C都在双曲线y=,点C的横坐标为:=6,故C(6,)
∴S△OCN=S△AOM=5,
由=,
得:S△AOB=40,
则△AOB面积为40.
24.证明:将△ABQ绕A点顺时针旋转90°得到△ACQ′,连接PQ′,
∴AQ′=AQ,CQ′=BQ,∠BAQ=∠CAQ′,∠ACQ′=∠ABC,
∵四边形ABCD为正方形,
∴∠ACQ′=∠ABC=∠ACB=45°,∠CAB=90°,
∵∠MAN=45°,
∴∠CAP+∠BAQ=45°,
∴∠Q′AP=∠CAQ′+∠CAP=45°,
∴∠Q′AP=∠QAP,
在△Q′AP和△QAP中,
,
∴△Q′AP≌△QAP(SAS),
∴PQ=PQ′,
∵∠Q′CP=∠ACQ′+∠ACB=90°,
在Rt△Q′CP中,由勾股定理得,
Q′P2=Q′C2+CP2,
∴CP2+BQ2=PQ2.
1 / 13
