12.3.1等腰三角形(1)(浙江省台州市)
文档属性
| 名称 | 12.3.1等腰三角形(1)(浙江省台州市) |  | |
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-23 19:34:00 | ||
图片预览







文档简介
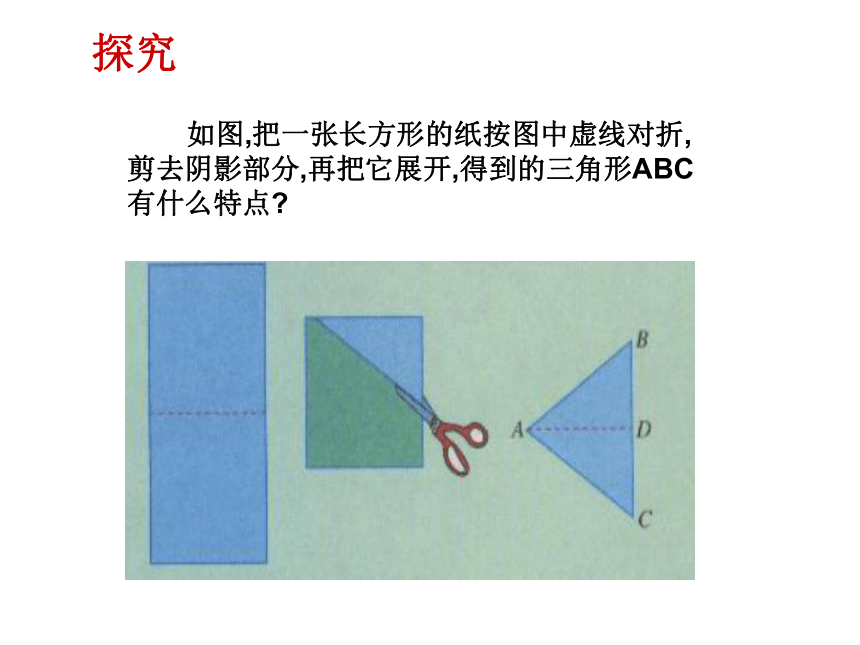
课件39张PPT。12.3.1等腰三角形探究 如图,把一张长方形的纸按图中虚线对折,
剪去阴影部分,再把它展开,得到的三角形ABC
有什么特点? 对于等腰三角形,你们已经了解了哪些方面的知识?问题 :你知道什么样的三角形是等腰三角形吗?
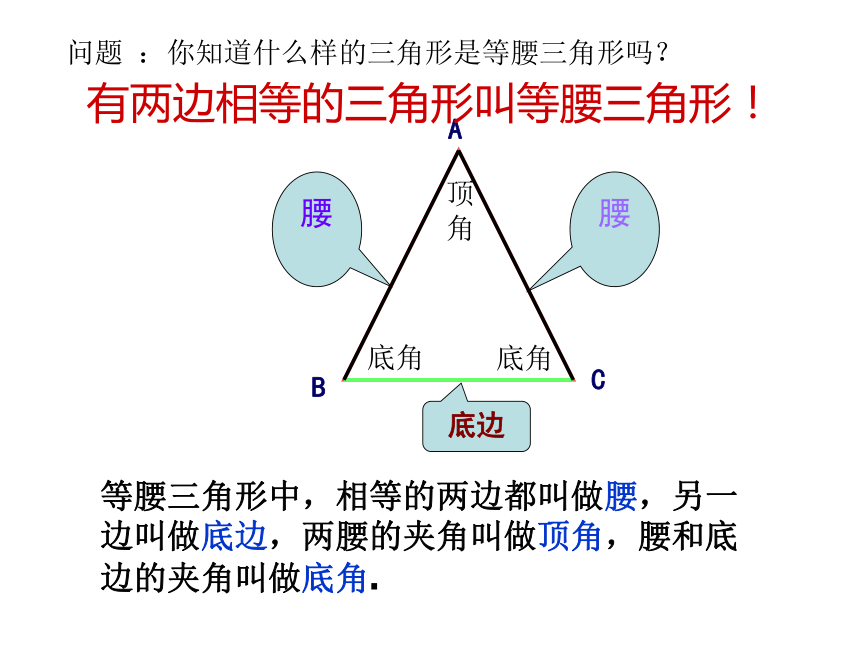
底边底角底角顶角等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.有两边相等的三角形叫等腰三角形!
1、等腰三角形一腰为3cm,底为4cm,则它的周长
是 ;
2、等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是 ;
3、等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
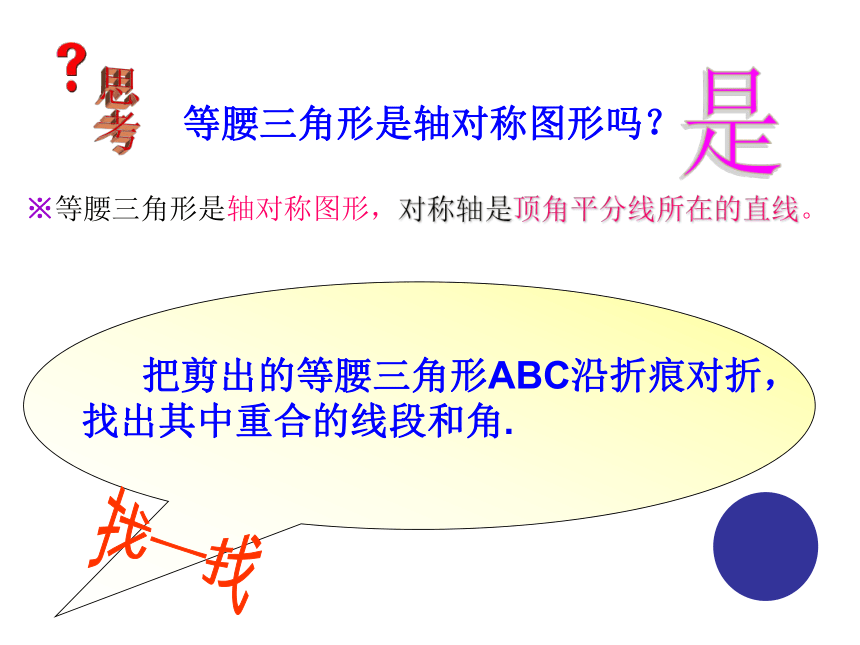
10 cm10 cm 或 11 cm19 cm小试牛刀 等腰三角形是轴对称图形吗?
思考是※等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线。请同学们观察下面的动画:ACDB请同学们观察下面的动画:ACBD请同学们观察下面的动画:ACBD请同学们观察下面的动画:ACBD请同学们观察下面的动画:ACBD请同学们观察下面的动画:请同学们观察下面的动画:C请同学们观察下面的动画:C请同学们观察下面的动画:c请同学们观察下面的动画:c请同学们观察下面的动画:C
AC B D AB=AC BD=CD AD=AD ∠B = ∠C.∠BAD = ∠CAD∠ADB = ∠ADC 等腰三角形除了两腰相等以外, 你还能发现它的其他性质吗? 大胆猜想猜想与论证等腰三角形的两个底角相等。已知:△ABC中,AB=AC求证:∠B=?C分析:1.如何证明两个角相等? 2.如何构造两个全等的三角形?猜想则有∠1=∠2D12在△ABD和△ACD中证明: 作顶角的平分线AD,AB=AC ∠1=∠2 AD=AD (公共边) ∴ △ABD≌ △ACD (SAS) ∴ ∠B=∠C (全等三角形对应角相等) 方法一则有 BD=CDD在△ABD和△ACD中证明: 作△ABC 的中线ADAB=AC BD=CDAD=AD (公共边) ∴ △ABD≌ △ACD (SSS) ∴ ∠B=∠C (全等三角形对应角相等) 方法二则有 ∠ADB=∠ADC =90oD在Rt△ABD和Rt△ACD中证明: 作△ABC 的高线ADAB=AC AD=AD (公共边) ∴ Rt△ABD≌Rt△ACD (HL) ∴ ∠B=∠C (全等三角形对应角相等) 方法三等腰三角形的性质1: 等腰三角形的两个底角相等
(简写成“等边对等角”)注意:
在 三角形中,等边对等角。用符号语言表示为: 在△ABC中,
∵ AC=AB( )
∴ ∠B=∠C ( )已知等边对等角⒈等腰三角形一个底角为75°,它的另外两个
角为_____ __;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个角
为______ __。75°, 30°70°,40°或55°,55°35°,35°小试牛刀想一想: 刚才的证明除了能得到∠B=∠C 你还能发现什么?
A B D C AB=AC BD=CD AD=AD ∠B = ∠C.∠BAD = ∠CAD ∠ADB =∠ADC=90°等腰三角形顶角的平分线、底边上的中线、底边上的高相互重合。性质2(等腰三角形三线合一)是真是假 等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。 等腰三角形“三线合一”的性质用符号语言表示为:12B DCD12ADBCADBCB DCD1 .如图,在△ABC中,AB=AC, BD=CD,∠BAC=100o,则∠BAD= ______ 2 .如图,在△ABC中,AB=AC, AD平分∠BAC, BC=10则BD= ______50o5例:如图,这是正在修建的南充嘉陵江三桥设计效果图,桥梁支架与桥面形成的△ABC中,AB=AC , AC上有一点D,测得BD=BC=AD,求△ABC 中∠A 的度数. 教学流程 一次数学课上,老师布置了一道几何证明题,通过大家的激烈讨论得到了许多种证明方法,聪明的你们,能找出几种证明方法呢?试试看吧! 如图,已知△ABC中,AB=AC,F在AC上,在BA的延长线上截取AE=AF,求证:ED⊥BC天生我才 如图在等腰三角形ABC中,AB =AC.点D为BC的中点.AEDCBF(1)猜想一下:点D到两腰的距离DE与DF相等吗?(2)如果DE、DF分别是AB、AC上的中线,它们还相等吗?探一探(3)如果DE、DF是∠ADB、 ∠ ADC的平分线,它们还相等吗? 如图在等腰三角形ABC中,AB =AC.点D为BC的中点.(1)猜想一下:点D到两腰的距离DE与DF相等吗?(2)如果DE、DF分别是AB、AC上的中线,它们还相等吗?问题拓展(3)如果将点D沿DA由D向A运动到D′那么点D′到两腰的距离还相等吗?试说明理由.(2)如果DE、DF是∠ADB、 ∠ ADC的平分线,它们还相等吗?ADCB● 1 、掌握等腰三角形的两个性质及简单应用 2、熟练求解等腰三角形的顶角、底角的度数;
3 、注意:解决等腰三角形有关计算有时要利
用方程来解决
谢谢
剪去阴影部分,再把它展开,得到的三角形ABC
有什么特点? 对于等腰三角形,你们已经了解了哪些方面的知识?问题 :你知道什么样的三角形是等腰三角形吗?
底边底角底角顶角等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.有两边相等的三角形叫等腰三角形!
1、等腰三角形一腰为3cm,底为4cm,则它的周长
是 ;
2、等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是 ;
3、等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
10 cm10 cm 或 11 cm19 cm小试牛刀 等腰三角形是轴对称图形吗?
思考是※等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线。请同学们观察下面的动画:ACDB请同学们观察下面的动画:ACBD请同学们观察下面的动画:ACBD请同学们观察下面的动画:ACBD请同学们观察下面的动画:ACBD请同学们观察下面的动画:请同学们观察下面的动画:C请同学们观察下面的动画:C请同学们观察下面的动画:c请同学们观察下面的动画:c请同学们观察下面的动画:C
AC B D AB=AC BD=CD AD=AD ∠B = ∠C.∠BAD = ∠CAD∠ADB = ∠ADC 等腰三角形除了两腰相等以外, 你还能发现它的其他性质吗? 大胆猜想猜想与论证等腰三角形的两个底角相等。已知:△ABC中,AB=AC求证:∠B=?C分析:1.如何证明两个角相等? 2.如何构造两个全等的三角形?猜想则有∠1=∠2D12在△ABD和△ACD中证明: 作顶角的平分线AD,AB=AC ∠1=∠2 AD=AD (公共边) ∴ △ABD≌ △ACD (SAS) ∴ ∠B=∠C (全等三角形对应角相等) 方法一则有 BD=CDD在△ABD和△ACD中证明: 作△ABC 的中线ADAB=AC BD=CDAD=AD (公共边) ∴ △ABD≌ △ACD (SSS) ∴ ∠B=∠C (全等三角形对应角相等) 方法二则有 ∠ADB=∠ADC =90oD在Rt△ABD和Rt△ACD中证明: 作△ABC 的高线ADAB=AC AD=AD (公共边) ∴ Rt△ABD≌Rt△ACD (HL) ∴ ∠B=∠C (全等三角形对应角相等) 方法三等腰三角形的性质1: 等腰三角形的两个底角相等
(简写成“等边对等角”)注意:
在 三角形中,等边对等角。用符号语言表示为: 在△ABC中,
∵ AC=AB( )
∴ ∠B=∠C ( )已知等边对等角⒈等腰三角形一个底角为75°,它的另外两个
角为_____ __;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个角
为______ __。75°, 30°70°,40°或55°,55°35°,35°小试牛刀想一想: 刚才的证明除了能得到∠B=∠C 你还能发现什么?
A B D C AB=AC BD=CD AD=AD ∠B = ∠C.∠BAD = ∠CAD ∠ADB =∠ADC=90°等腰三角形顶角的平分线、底边上的中线、底边上的高相互重合。性质2(等腰三角形三线合一)是真是假 等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。 等腰三角形“三线合一”的性质用符号语言表示为:12B DCD12ADBCADBCB DCD1 .如图,在△ABC中,AB=AC, BD=CD,∠BAC=100o,则∠BAD= ______ 2 .如图,在△ABC中,AB=AC, AD平分∠BAC, BC=10则BD= ______50o5例:如图,这是正在修建的南充嘉陵江三桥设计效果图,桥梁支架与桥面形成的△ABC中,AB=AC , AC上有一点D,测得BD=BC=AD,求△ABC 中∠A 的度数. 教学流程 一次数学课上,老师布置了一道几何证明题,通过大家的激烈讨论得到了许多种证明方法,聪明的你们,能找出几种证明方法呢?试试看吧! 如图,已知△ABC中,AB=AC,F在AC上,在BA的延长线上截取AE=AF,求证:ED⊥BC天生我才 如图在等腰三角形ABC中,AB =AC.点D为BC的中点.AEDCBF(1)猜想一下:点D到两腰的距离DE与DF相等吗?(2)如果DE、DF分别是AB、AC上的中线,它们还相等吗?探一探(3)如果DE、DF是∠ADB、 ∠ ADC的平分线,它们还相等吗? 如图在等腰三角形ABC中,AB =AC.点D为BC的中点.(1)猜想一下:点D到两腰的距离DE与DF相等吗?(2)如果DE、DF分别是AB、AC上的中线,它们还相等吗?问题拓展(3)如果将点D沿DA由D向A运动到D′那么点D′到两腰的距离还相等吗?试说明理由.(2)如果DE、DF是∠ADB、 ∠ ADC的平分线,它们还相等吗?ADCB● 1 、掌握等腰三角形的两个性质及简单应用 2、熟练求解等腰三角形的顶角、底角的度数;
3 、注意:解决等腰三角形有关计算有时要利
用方程来解决
谢谢
