人教版数学九年级下册 27.2.1相似三角形的判定巩固 学案(含答案)
文档属性
| 名称 | 人教版数学九年级下册 27.2.1相似三角形的判定巩固 学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 191.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 09:08:17 | ||
图片预览


文档简介
相似三角形的判定——巩固拓展
班级: 姓名: 组号:
一、巩固训练
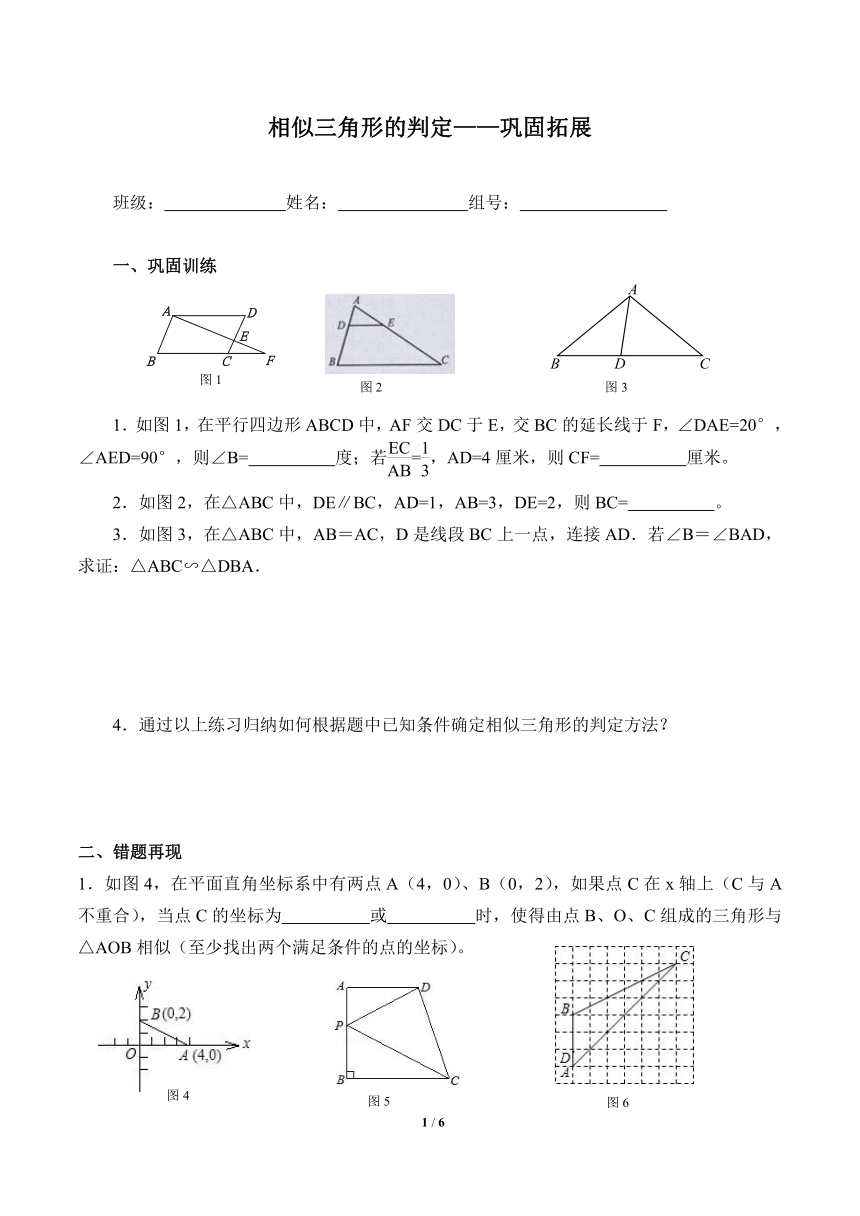
1.如图1,在平行四边形ABCD中,AF交DC于E,交BC的延长线于F,∠DAE=20°,∠AED=90°,则∠B= 度;若=,AD=4厘米,则CF= 厘米。
2.如图2,在△ABC中,DE∥BC,AD=1,AB=3,DE=2,则BC= 。
3.如图3,在△ABC中,AB=AC,D是线段BC上一点,连接AD.若∠B=∠BAD,求证:△ABC∽△DBA.
4.通过以上练习归纳如何根据题中已知条件确定相似三角形的判定方法?
二、错题再现
1.如图4,在平面直角坐标系中有两点A(4,0)、B(0,2),如果点C在x轴上(C与A不重合),当点C的坐标为 或 时,使得由点B、O、C组成的三角形与△AOB相似(至少找出两个满足条件的点的坐标)。
2.如图5,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB上一个动点,当PC+PD的和最小时,PB的长为
3.如图6,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点。如果AD=1,那么当AE= 时,以点A、D、E为顶点的三角形与△ABC相似。
三、综合运用
1.如图7,在直角坐标系中,点A(0,4),B(3,4),C(6,0),动点P从点A出发以1个单位/秒的速度在y轴上向下运动,动点Q同时从点C出发以2个单位/秒的速度在x轴上向左运动,过点P作RP⊥y轴,交OB于R,连结RQ。当点P与点O重合时,两动点均停止运动。设运动的时间为t秒。
(1)若t=1,求点R的坐标;
(2)在线段OB上是否存在点R,使△ORQ与△ABC相似?若存在,请求出所有满足要求的t的值;若不存在,请说明理由。
四、精练反馈:
A组
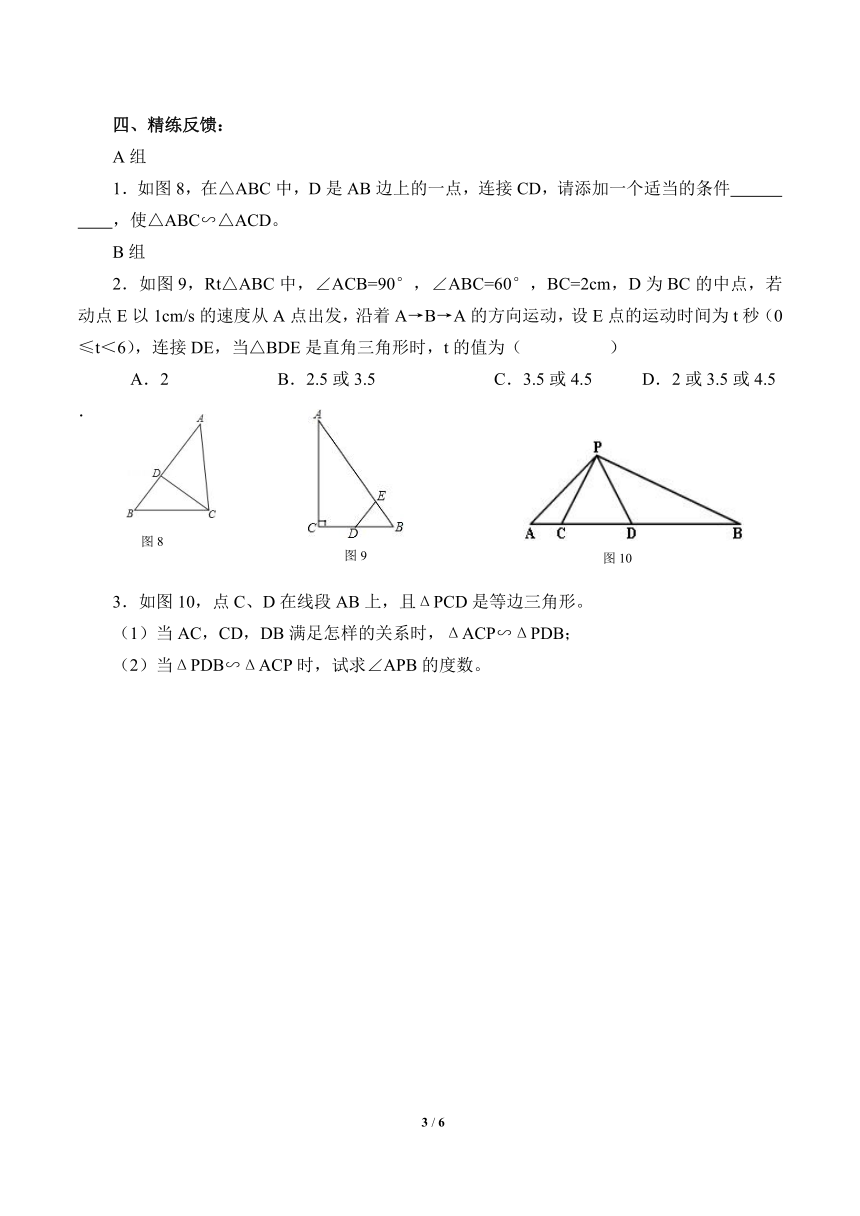
1.如图8,在△ABC中,D是AB边上的一点,连接CD,请添加一个适当的条件 ,使△ABC∽△ACD。
B组
2.如图9,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )
A. A.2 B B.2.5或3.5 C C.3.5或4.5 D D.2或3.5或4.5
3.如图10,点C、D在线段AB上,且ΔPCD是等边三角形。
(1)当AC,CD,DB满足怎样的关系时,ΔACP∽ΔPDB;
(2)当ΔPDB∽ΔACP时,试求∠APB的度数。
【答案】
巩固训练
1.70;2
2.6
3.证明:∵AB=AC,AD=BD
∴∠B=∠C,∠B=∠BAD,
∴△ABC∽△DBA.
4.略
错题再现
1.(1,0);(-1,0)
2.3
3.
综合运用
1.解:(1)∵A(0,4),B(3,4),
∴AB⊥y轴,AB=3.
∵RP⊥y轴,
∴∠OPR=∠OAB=90° 。
又∠POR=∠AOB,
∴△OPR∽△OAB ,
∴ 。
当t=1时,AP=1,OP=3,
∴,
∵R的纵坐标等于OP的长,∴点R的坐标为(,3)。
(2)如图a,过点B作BD⊥x轴于点D,则D(3,0)
在△BOC中,
∵OD=DC=3,且BD⊥OC,
∴OB=BC.
∵△OPR∽△OAB,
∴,
∵在Rt△OBD中,
∴,
∴。
由题意得,AP=t,CQ=2t (0≤t≤4)。
分三种情况讨论:
①当0≤t<3时,即点Q从点C运动到点O(不与O重合)时,
∵OB=BC
∴∠BOC=∠BCO>∠BCA
∵AB∥x轴,
∴∠BOC =∠ABO,∠BAC=∠ACO,
∵∠ABO<ABC, ∠BCO>∠ACO,
∴∠BOC<ABC, ∠BOC>∠BAC,
∴当0≤t<3时,△ORQ与△ABC不可能相似。
②当t=3时,点Q与O重合时,△ORQ变成线段OR,故不可能与△ABC相似
③如图b,当3<t≤4时,即点Q从原点O向左运动时,
∵BD∥y轴
∴∠AOB=∠OBD
∵OB=BC,BD⊥OC
∴∠OBD=∠DBC
∴∠QOR=90°+∠AOB=90°+∠DBC=∠ABC
当时,
∵,
∴,
∴。
当时,
同理可求得。
经检验和均在3<t≤4内,
∴所有满足要求的t的值为和。
精练反馈:
1.∠ACD=∠B
2.D
3.解:(1)当CD2=AC·DB时,△ACP∽△PDB,
∵△PCD是等边三角形,∴∠PCD=∠PDC=60°,
∴∠ACP=∠PDB=120°,
若CD2=AC·DB,可得:PC·PD=AC·DB,
即=,则△ACP∽△PDB
(2)当△ACP∽△PDB时,∠APC=∠PBD
∵∠PDB=120°∴∠DPB+∠DBP=60°
∴∠APC+∠BPD=60°
∴∠APB=∠CPD+∠APC+∠BPD=120°
6 / 6
班级: 姓名: 组号:
一、巩固训练
1.如图1,在平行四边形ABCD中,AF交DC于E,交BC的延长线于F,∠DAE=20°,∠AED=90°,则∠B= 度;若=,AD=4厘米,则CF= 厘米。
2.如图2,在△ABC中,DE∥BC,AD=1,AB=3,DE=2,则BC= 。
3.如图3,在△ABC中,AB=AC,D是线段BC上一点,连接AD.若∠B=∠BAD,求证:△ABC∽△DBA.
4.通过以上练习归纳如何根据题中已知条件确定相似三角形的判定方法?
二、错题再现
1.如图4,在平面直角坐标系中有两点A(4,0)、B(0,2),如果点C在x轴上(C与A不重合),当点C的坐标为 或 时,使得由点B、O、C组成的三角形与△AOB相似(至少找出两个满足条件的点的坐标)。
2.如图5,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB上一个动点,当PC+PD的和最小时,PB的长为
3.如图6,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点。如果AD=1,那么当AE= 时,以点A、D、E为顶点的三角形与△ABC相似。
三、综合运用
1.如图7,在直角坐标系中,点A(0,4),B(3,4),C(6,0),动点P从点A出发以1个单位/秒的速度在y轴上向下运动,动点Q同时从点C出发以2个单位/秒的速度在x轴上向左运动,过点P作RP⊥y轴,交OB于R,连结RQ。当点P与点O重合时,两动点均停止运动。设运动的时间为t秒。
(1)若t=1,求点R的坐标;
(2)在线段OB上是否存在点R,使△ORQ与△ABC相似?若存在,请求出所有满足要求的t的值;若不存在,请说明理由。
四、精练反馈:
A组
1.如图8,在△ABC中,D是AB边上的一点,连接CD,请添加一个适当的条件 ,使△ABC∽△ACD。
B组
2.如图9,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )
A. A.2 B B.2.5或3.5 C C.3.5或4.5 D D.2或3.5或4.5
3.如图10,点C、D在线段AB上,且ΔPCD是等边三角形。
(1)当AC,CD,DB满足怎样的关系时,ΔACP∽ΔPDB;
(2)当ΔPDB∽ΔACP时,试求∠APB的度数。
【答案】
巩固训练
1.70;2
2.6
3.证明:∵AB=AC,AD=BD
∴∠B=∠C,∠B=∠BAD,
∴△ABC∽△DBA.
4.略
错题再现
1.(1,0);(-1,0)
2.3
3.
综合运用
1.解:(1)∵A(0,4),B(3,4),
∴AB⊥y轴,AB=3.
∵RP⊥y轴,
∴∠OPR=∠OAB=90° 。
又∠POR=∠AOB,
∴△OPR∽△OAB ,
∴ 。
当t=1时,AP=1,OP=3,
∴,
∵R的纵坐标等于OP的长,∴点R的坐标为(,3)。
(2)如图a,过点B作BD⊥x轴于点D,则D(3,0)
在△BOC中,
∵OD=DC=3,且BD⊥OC,
∴OB=BC.
∵△OPR∽△OAB,
∴,
∵在Rt△OBD中,
∴,
∴。
由题意得,AP=t,CQ=2t (0≤t≤4)。
分三种情况讨论:
①当0≤t<3时,即点Q从点C运动到点O(不与O重合)时,
∵OB=BC
∴∠BOC=∠BCO>∠BCA
∵AB∥x轴,
∴∠BOC =∠ABO,∠BAC=∠ACO,
∵∠ABO<ABC, ∠BCO>∠ACO,
∴∠BOC<ABC, ∠BOC>∠BAC,
∴当0≤t<3时,△ORQ与△ABC不可能相似。
②当t=3时,点Q与O重合时,△ORQ变成线段OR,故不可能与△ABC相似
③如图b,当3<t≤4时,即点Q从原点O向左运动时,
∵BD∥y轴
∴∠AOB=∠OBD
∵OB=BC,BD⊥OC
∴∠OBD=∠DBC
∴∠QOR=90°+∠AOB=90°+∠DBC=∠ABC
当时,
∵,
∴,
∴。
当时,
同理可求得。
经检验和均在3<t≤4内,
∴所有满足要求的t的值为和。
精练反馈:
1.∠ACD=∠B
2.D
3.解:(1)当CD2=AC·DB时,△ACP∽△PDB,
∵△PCD是等边三角形,∴∠PCD=∠PDC=60°,
∴∠ACP=∠PDB=120°,
若CD2=AC·DB,可得:PC·PD=AC·DB,
即=,则△ACP∽△PDB
(2)当△ACP∽△PDB时,∠APC=∠PBD
∵∠PDB=120°∴∠DPB+∠DBP=60°
∴∠APC+∠BPD=60°
∴∠APB=∠CPD+∠APC+∠BPD=120°
6 / 6
