5.2.1 三角函数的概念(第二课时)(共20页ppt)
文档属性
| 名称 | 5.2.1 三角函数的概念(第二课时)(共20页ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-09 08:48:26 | ||
图片预览







文档简介
(共20张PPT)
第5章 三角函数
5.2 三角函数的概念
5.2.1 三角函数的概念(第二课时)
人教A版(2019)
教学目标
学习目标 数学素养
1.利用三角函数的概念,判定三角函数在各个象限的符号; 1.直观想象素养.
2.掌握并会用诱导公式(一); 2.数学运算素养.
3.掌握简单的三角函数求值.
温故知新
-32°
1. 三角函数的定义1.
设α是一个任意角,点P(x, y)是α的终边与单位圆的交点,则
2. 三角函数的定义2.
设α是一个任意角,在α的终边上任取(异于原点的)一点P(x, y),P与原点的距离为
温故知新
3.三角函数三要素
定义域
对应关系
值域
R
x(弧度数) 角的终边与单位圆交点的纵坐标
[-1,1]
x(弧度数) 角的终边与单位圆交点的横坐标
R
[-1,1]
x(弧度数) 角的终边与单位圆交点的纵坐标与横坐标的比值
R
新知探究
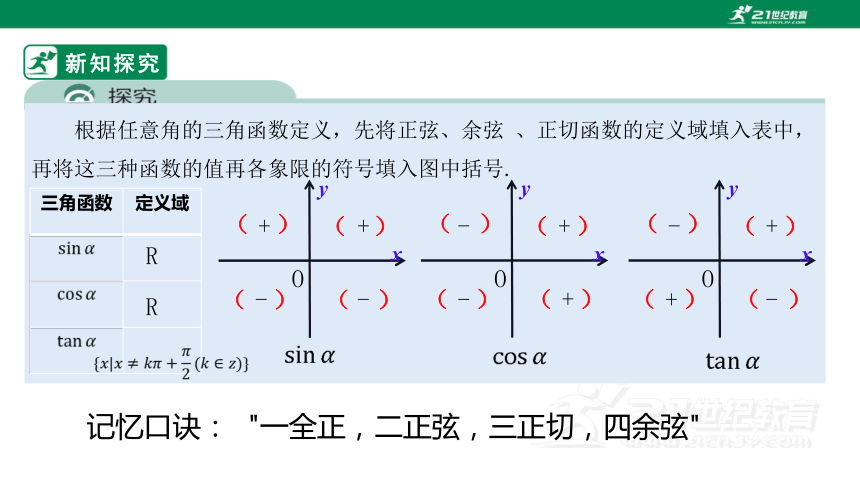
根据任意角的三角函数定义,先将正弦、余弦 、正切函数的定义域填入表中,再将这三种函数的值再各象限的符号填入图中括号.
三角函数 定义域
y
x
O
( )
( )
( )
( )
y
x
O
( )
( )
( )
( )
y
x
O
( )
( )
( )
( )
R
R
+
+
-
-
+
-
-
+
+
-
+
-
记忆口诀: "一全正,二正弦,三正切,四余弦"
新知探究
角α 0° 90° 180° 270° 360°
角α的弧度数
sinα
cosα
tanα
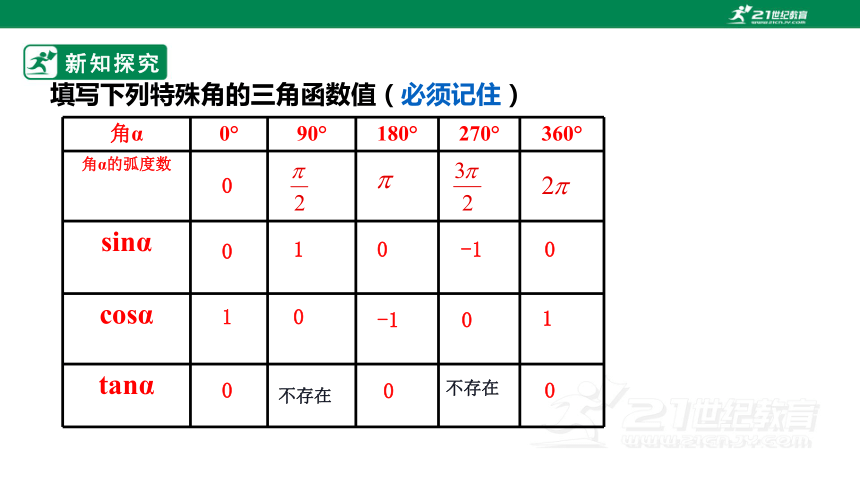
填写下列特殊角的三角函数值(必须记住)
0
0
1
0
-1
0
1
0
-1
0
1
0
不存在
0
0
不存在
新知形成
【例1】求证:角θ为第三象限角的充要条件为
证明:
首先证明充分性,
因为①式sinθ<0成立,所以θ角的终边位于第三或者第四象限,也可能和y轴的负半轴重合;
又因为②式cosθ>0成立,所以θ角的终边位于第一或者第三象限,
因为①②式都成立,所以θ角的终边只能位于第三象限.于是角θ为第三象限角.
再证明必要性,
因为角θ是第三象限角,根据定义有sinθ<0, tanθ>0,
所以必要性成立,即充要性成立.
新知形成
由三角函数的定义,可以知道:终边相同的角的同一三角函数相等.
由此得到一组公式:
诱导公式一
其中k∈z.
由诱导公式一可知,三角函数值有“周而复始”的变化规律,即角α的终边每绕原点旋转一周,函数值将重复出现一次.
利用诱导公式一,可以把任意角的三角函数值,转化为求0~2(或0°~360°)角的三角函数值.
新知形成
诱导公式一
其中k∈z.
注意:利用诱导公式一时,角度制与弧度制不能混用.
诱导公式一也可以用角度制表示.
新知探求
【例2】确定下列三角函数值的符号,然后用计算工具验证:
(1)cos250 ; (2)
(3)tan(-672 ); (4)
解:
⑴因为250 是第三象限角,所以cos250 <0.
⑵因为是第四象限角,所以.
⑶因为,
⑷因为
而48°是第一象限角,所以.
而的终边在x轴上,所以.
请同学们自己完成用计算工具验证.
新知探求
【例3】求下列三角函数值:
⑴(精确到0.001); ⑵ ;
⑶
解:
⑵
⑶
⑴
新知探求
【例4】求下列各式的值:
⑴sin(-1 395°)cos 1 110°+cos(-1 020°)sin 750°;
解:
⑴原式=
+
新知探求
【例4】求下列各式的值:
⑵
解:
⑵原式=
=1
注意:
1.利用诱导公式一可把任意角的三角函数值化归为区间[0,2π)上角的三角函数值,实现“负化正,大化小”,体现了数学中的转化与化归思想.
2.要熟记一些特殊角的三角函数值,有利于准确求值.
初试身手
1.的值是( )
A. B. C. D.
2.若三角形的两内角 , 满足sin cos <0,则此三角形必为( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.以上三种情况都可能
3.若是第三象限角,则下列各式中不成立的是( )
A.sin +cos <0 B.tan sin <0
C.cos tan <0 D.tan -cos >0
A
B
2.解:
因为三角形的两内角 , 满足sin cos <0,
所以cos <0,角 为钝角,此三角形必为钝角三角形 .故选B.
3.解:
由是第三象限角,得sin <0,cos <0,tan >0 ,则sin +cos <0,
tan sin >0,cos tan <0 ,tan -cos >0,故选B.
B
初试身手
4.sin2·cos3·tan4的值 ( )
A.大于0 B.小于0 C.等于0 D.大于等于0
5.若sinθ·cosθ>0, 则θ是第 象限的角.
6.求值:sin(-1320°)cos1110°+cos(-1020°)sin750°+tan495°.
解:
4.因为2和3都是第二象限角,4是第三象限角,即sin2>0,cos3<0,tan4>0,
所以sin2·cos3·tan4<0,故选B.
B
5.因为sinθ·cosθ>0,即sinθ与cosθ同号,
所以θ是第一、三象限角.
一、三
6.原式=
=
=
课堂小结
三角函数值的符号:
正弦函数值:一、二象限正,三、四象限负
余弦函数值:一、四象限正,二、三象限负
正切函数值:一、三象限正,二、四象限负
诱导公式一
其中k∈z.
利用诱导公式一,可以把任意角的三角函数值,转化为求0~2(或0°~360°)角的三角函数值.
作业布置
作业:p185 习题5.2 第5⑵⑷⑹,8⑴⑷,9⑴⑵,10⑴⑶题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第5章 三角函数
5.2 三角函数的概念
5.2.1 三角函数的概念(第二课时)
人教A版(2019)
教学目标
学习目标 数学素养
1.利用三角函数的概念,判定三角函数在各个象限的符号; 1.直观想象素养.
2.掌握并会用诱导公式(一); 2.数学运算素养.
3.掌握简单的三角函数求值.
温故知新
-32°
1. 三角函数的定义1.
设α是一个任意角,点P(x, y)是α的终边与单位圆的交点,则
2. 三角函数的定义2.
设α是一个任意角,在α的终边上任取(异于原点的)一点P(x, y),P与原点的距离为
温故知新
3.三角函数三要素
定义域
对应关系
值域
R
x(弧度数) 角的终边与单位圆交点的纵坐标
[-1,1]
x(弧度数) 角的终边与单位圆交点的横坐标
R
[-1,1]
x(弧度数) 角的终边与单位圆交点的纵坐标与横坐标的比值
R
新知探究
根据任意角的三角函数定义,先将正弦、余弦 、正切函数的定义域填入表中,再将这三种函数的值再各象限的符号填入图中括号.
三角函数 定义域
y
x
O
( )
( )
( )
( )
y
x
O
( )
( )
( )
( )
y
x
O
( )
( )
( )
( )
R
R
+
+
-
-
+
-
-
+
+
-
+
-
记忆口诀: "一全正,二正弦,三正切,四余弦"
新知探究
角α 0° 90° 180° 270° 360°
角α的弧度数
sinα
cosα
tanα
填写下列特殊角的三角函数值(必须记住)
0
0
1
0
-1
0
1
0
-1
0
1
0
不存在
0
0
不存在
新知形成
【例1】求证:角θ为第三象限角的充要条件为
证明:
首先证明充分性,
因为①式sinθ<0成立,所以θ角的终边位于第三或者第四象限,也可能和y轴的负半轴重合;
又因为②式cosθ>0成立,所以θ角的终边位于第一或者第三象限,
因为①②式都成立,所以θ角的终边只能位于第三象限.于是角θ为第三象限角.
再证明必要性,
因为角θ是第三象限角,根据定义有sinθ<0, tanθ>0,
所以必要性成立,即充要性成立.
新知形成
由三角函数的定义,可以知道:终边相同的角的同一三角函数相等.
由此得到一组公式:
诱导公式一
其中k∈z.
由诱导公式一可知,三角函数值有“周而复始”的变化规律,即角α的终边每绕原点旋转一周,函数值将重复出现一次.
利用诱导公式一,可以把任意角的三角函数值,转化为求0~2(或0°~360°)角的三角函数值.
新知形成
诱导公式一
其中k∈z.
注意:利用诱导公式一时,角度制与弧度制不能混用.
诱导公式一也可以用角度制表示.
新知探求
【例2】确定下列三角函数值的符号,然后用计算工具验证:
(1)cos250 ; (2)
(3)tan(-672 ); (4)
解:
⑴因为250 是第三象限角,所以cos250 <0.
⑵因为是第四象限角,所以.
⑶因为,
⑷因为
而48°是第一象限角,所以.
而的终边在x轴上,所以.
请同学们自己完成用计算工具验证.
新知探求
【例3】求下列三角函数值:
⑴(精确到0.001); ⑵ ;
⑶
解:
⑵
⑶
⑴
新知探求
【例4】求下列各式的值:
⑴sin(-1 395°)cos 1 110°+cos(-1 020°)sin 750°;
解:
⑴原式=
+
新知探求
【例4】求下列各式的值:
⑵
解:
⑵原式=
=1
注意:
1.利用诱导公式一可把任意角的三角函数值化归为区间[0,2π)上角的三角函数值,实现“负化正,大化小”,体现了数学中的转化与化归思想.
2.要熟记一些特殊角的三角函数值,有利于准确求值.
初试身手
1.的值是( )
A. B. C. D.
2.若三角形的两内角 , 满足sin cos <0,则此三角形必为( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.以上三种情况都可能
3.若是第三象限角,则下列各式中不成立的是( )
A.sin +cos <0 B.tan sin <0
C.cos tan <0 D.tan -cos >0
A
B
2.解:
因为三角形的两内角 , 满足sin cos <0,
所以cos <0,角 为钝角,此三角形必为钝角三角形 .故选B.
3.解:
由是第三象限角,得sin <0,cos <0,tan >0 ,则sin +cos <0,
tan sin >0,cos tan <0 ,tan -cos >0,故选B.
B
初试身手
4.sin2·cos3·tan4的值 ( )
A.大于0 B.小于0 C.等于0 D.大于等于0
5.若sinθ·cosθ>0, 则θ是第 象限的角.
6.求值:sin(-1320°)cos1110°+cos(-1020°)sin750°+tan495°.
解:
4.因为2和3都是第二象限角,4是第三象限角,即sin2>0,cos3<0,tan4>0,
所以sin2·cos3·tan4<0,故选B.
B
5.因为sinθ·cosθ>0,即sinθ与cosθ同号,
所以θ是第一、三象限角.
一、三
6.原式=
=
=
课堂小结
三角函数值的符号:
正弦函数值:一、二象限正,三、四象限负
余弦函数值:一、四象限正,二、三象限负
正切函数值:一、三象限正,二、四象限负
诱导公式一
其中k∈z.
利用诱导公式一,可以把任意角的三角函数值,转化为求0~2(或0°~360°)角的三角函数值.
作业布置
作业:p185 习题5.2 第5⑵⑷⑹,8⑴⑷,9⑴⑵,10⑴⑶题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
