人教版数学九年级下册 27.3位似 学案(含答案)
文档属性
| 名称 | 人教版数学九年级下册 27.3位似 学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 387.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 10:27:24 | ||
图片预览


文档简介
位似
班级: 姓名: 组号:
第二课时
一、旧知回顾
1.如图1,以C为位似中心,把△ABC放大2倍的△DEF且点B的对应点E在点C的另一侧。若点A的坐标为(-4,2),试通过计算求对应点D的坐标。
二、新知梳理
2.在平面直角坐标系中有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小。
方法一: 方法二:
探究:(1)在方法一中,A'的坐标是 ,B'的坐标是 ,对应点坐标之比是
(2)在方法二中,A''的坐标是 ,B''的坐标是 ,对应点坐标之比是 。
归纳:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于 ;
3.图形变换:我们学习过的图形变换包括: ,轴对称,旋转和
4.如图2,四边形ABCD顶点坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形,并写出A'、B'、C'、
D'三点对应点的坐标。
★通过预习你还有什么困惑?
一、课堂活动、记录
平面直角坐标系中把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律。
二、精练反馈
1.如图3所示,左图与右图是相似图形,如果左图上一个顶点坐标是(a,b),那么右图上对应顶点的坐标是( )
A.(-a,-2b) B.(-2a,-b) C.(-2a,-2b) D.(-2b,-2a)
2.如图4所示,已知△OAB与△OA1B1是相似比为1:2的人位似图形,点O是位似中心,若△OAB内的点P(x,y)与△OA1B1内的点P1对应,则P1的坐标是
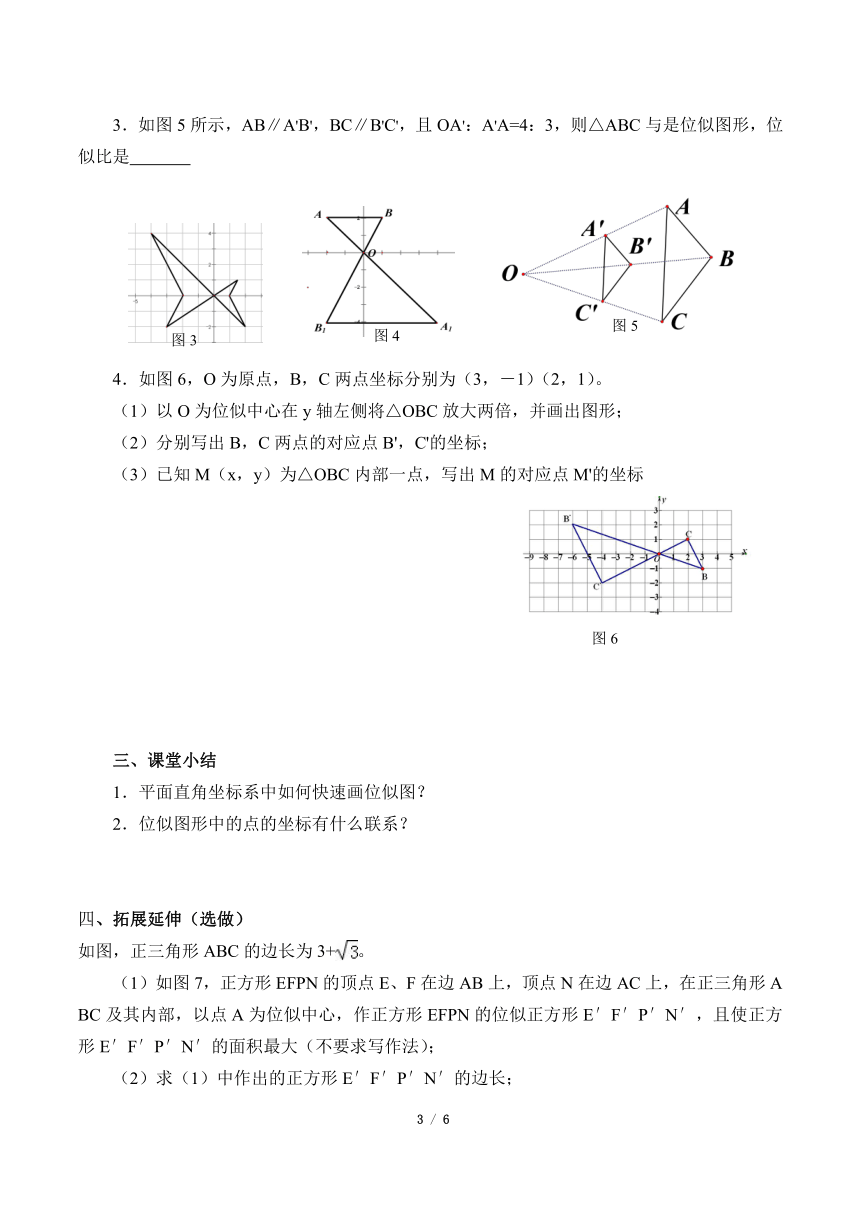
3.如图5所示,AB∥A'B',BC∥B'C',且OA':A'A=4:3,则△ABC与是位似图形,位似比是
4.如图6,O为原点,B,C两点坐标分别为(3,-1)(2,1)。
(1)以O为位似中心在y轴左侧将△OBC放大两倍,并画出图形;
(2)分别写出B,C两点的对应点B',C'的坐标;
(3)已知M(x,y)为△OBC内部一点,写出M的对应点M'的坐标
三、课堂小结
1.平面直角坐标系中如何快速画位似图?
2.位似图形中的点的坐标有什么联系?
四、拓展延伸(选做)
如图,正三角形ABC的边长为3+。
(1)如图7,正方形EFPN的顶点E、F在边AB上,顶点N在边AC上,在正三角形ABC及其内部,以点A为位似中心,作正方形EFPN的位似正方形E′F′P′N′,且使正方形E′F′P′N′的面积最大(不要求写作法);
(2)求(1)中作出的正方形E′F′P′N′的边长;
(3)如图8,在正三角形ABC中放入正方形DEMN和正方形EFPH,使得DE、EF在边AB上,点P、N分别在边CB.CA上,求这两个正方形面积和的最大值和最小值,并说明理由。
【答案】
【学前准备】
1.解:D(8-,4)
2.探究:(1)(2,1);(2,0);
(2)(-2,-2);(-2,-1);(-2,0)
归纳:K或-K
3.平移;相似
4.
解:
【课堂探究】
课堂活动、记录
略
精练反馈
1.C
2.P(-2x,-2y)
3.7:4
4.解:(1)△OB'C'如图所示;
(2)B'(-6,2),C'(-4,-2)
(3)
课堂小结
略
拓展延伸
解:(1)如图①,正方形E′F′P′N′即为所求。
(2)设正方形E′F′P′N′的边长为x,∵△ABC为正三角形,∴AE′=BF′=x。
∵E′F′+AE′+BF′=AB,∴x+x+x=3+,∴x=,即x=3-3,
(3)如图②,连接NE、EP、PN,则∠NEP=90°。
设正方形DEMN、正方形EFPH的边长分别为m、n(m≥n),它们的面积和为S,则NE=,PE=n。
∴PN2=NE2+PE2=2m2+2n2=2(m2+n2)。
∴S=m2+n2=PN2,延长PH交ND于点G,则PG⊥ND.
在Rt△PGN中,PN2=PG2+GN2=(m+n)2+(m-n)2.
∵AD+DE+EF+BF=AB,即m+m+n+n=+3,化简得m+n=3.
∴S=[32+(m-n)2]=+(m-n)2
①当(m-n)2=0时,即m=n时,S最小。
∴S最小=;
②当(m-n)2最大时,S最大。
即当m最大且n最小时,S最大。
∵m+n=3,由(2)知,m最大=3-3.
∴S最大=[9+2(m最大-n最小)]
=[9+(3-3-6+3)2]
=99-54…。
综上所述,S最大=99-54,S最小=。
6 / 6
班级: 姓名: 组号:
第二课时
一、旧知回顾
1.如图1,以C为位似中心,把△ABC放大2倍的△DEF且点B的对应点E在点C的另一侧。若点A的坐标为(-4,2),试通过计算求对应点D的坐标。
二、新知梳理
2.在平面直角坐标系中有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小。
方法一: 方法二:
探究:(1)在方法一中,A'的坐标是 ,B'的坐标是 ,对应点坐标之比是
(2)在方法二中,A''的坐标是 ,B''的坐标是 ,对应点坐标之比是 。
归纳:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于 ;
3.图形变换:我们学习过的图形变换包括: ,轴对称,旋转和
4.如图2,四边形ABCD顶点坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形,并写出A'、B'、C'、
D'三点对应点的坐标。
★通过预习你还有什么困惑?
一、课堂活动、记录
平面直角坐标系中把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律。
二、精练反馈
1.如图3所示,左图与右图是相似图形,如果左图上一个顶点坐标是(a,b),那么右图上对应顶点的坐标是( )
A.(-a,-2b) B.(-2a,-b) C.(-2a,-2b) D.(-2b,-2a)
2.如图4所示,已知△OAB与△OA1B1是相似比为1:2的人位似图形,点O是位似中心,若△OAB内的点P(x,y)与△OA1B1内的点P1对应,则P1的坐标是
3.如图5所示,AB∥A'B',BC∥B'C',且OA':A'A=4:3,则△ABC与是位似图形,位似比是
4.如图6,O为原点,B,C两点坐标分别为(3,-1)(2,1)。
(1)以O为位似中心在y轴左侧将△OBC放大两倍,并画出图形;
(2)分别写出B,C两点的对应点B',C'的坐标;
(3)已知M(x,y)为△OBC内部一点,写出M的对应点M'的坐标
三、课堂小结
1.平面直角坐标系中如何快速画位似图?
2.位似图形中的点的坐标有什么联系?
四、拓展延伸(选做)
如图,正三角形ABC的边长为3+。
(1)如图7,正方形EFPN的顶点E、F在边AB上,顶点N在边AC上,在正三角形ABC及其内部,以点A为位似中心,作正方形EFPN的位似正方形E′F′P′N′,且使正方形E′F′P′N′的面积最大(不要求写作法);
(2)求(1)中作出的正方形E′F′P′N′的边长;
(3)如图8,在正三角形ABC中放入正方形DEMN和正方形EFPH,使得DE、EF在边AB上,点P、N分别在边CB.CA上,求这两个正方形面积和的最大值和最小值,并说明理由。
【答案】
【学前准备】
1.解:D(8-,4)
2.探究:(1)(2,1);(2,0);
(2)(-2,-2);(-2,-1);(-2,0)
归纳:K或-K
3.平移;相似
4.
解:
【课堂探究】
课堂活动、记录
略
精练反馈
1.C
2.P(-2x,-2y)
3.7:4
4.解:(1)△OB'C'如图所示;
(2)B'(-6,2),C'(-4,-2)
(3)
课堂小结
略
拓展延伸
解:(1)如图①,正方形E′F′P′N′即为所求。
(2)设正方形E′F′P′N′的边长为x,∵△ABC为正三角形,∴AE′=BF′=x。
∵E′F′+AE′+BF′=AB,∴x+x+x=3+,∴x=,即x=3-3,
(3)如图②,连接NE、EP、PN,则∠NEP=90°。
设正方形DEMN、正方形EFPH的边长分别为m、n(m≥n),它们的面积和为S,则NE=,PE=n。
∴PN2=NE2+PE2=2m2+2n2=2(m2+n2)。
∴S=m2+n2=PN2,延长PH交ND于点G,则PG⊥ND.
在Rt△PGN中,PN2=PG2+GN2=(m+n)2+(m-n)2.
∵AD+DE+EF+BF=AB,即m+m+n+n=+3,化简得m+n=3.
∴S=[32+(m-n)2]=+(m-n)2
①当(m-n)2=0时,即m=n时,S最小。
∴S最小=;
②当(m-n)2最大时,S最大。
即当m最大且n最小时,S最大。
∵m+n=3,由(2)知,m最大=3-3.
∴S最大=[9+2(m最大-n最小)]
=[9+(3-3-6+3)2]
=99-54…。
综上所述,S最大=99-54,S最小=。
6 / 6
