人教版数学九年级下册 第二十七章 相似复习课时练(含答案)
文档属性
| 名称 | 人教版数学九年级下册 第二十七章 相似复习课时练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 137.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 12:36:15 | ||
图片预览


文档简介
人教九年级下 单元测试
第27章
班级________ 姓名________
一、单选题
1.如图,将图形用放大镜放大,这种图形的变化属于( )
A.平移 B.相似 C.旋转 D.对称
2.下列命题中,正确的是( )
A.如果一条直线截三角形两边的延长线所得的对应线段成比例,那么这条直线一定平行于三角形的第三边;
B.不同向量的单位向量的长度都相等,方向也都相同;
C.相似三角形的中线的比等于相似比;
D.一般来说,一条线段的黄金分割点有两个.
3.一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边是21,则其它两边的和是( ).
A.19 B.17 C.24 D.21
4.如图,已知 , ,以O为位似中心,把 缩小到原来的 ,则点E的对应点的坐标为是( )
A. B. 或
C. 或 D.
5.在同一时刻,身高1.6m的小强在阳光下的影长为0.8m,一棵大树的影长为4.8m,则树的高度为( )
A.4.8m B.6.4m C.9.6m D.10m
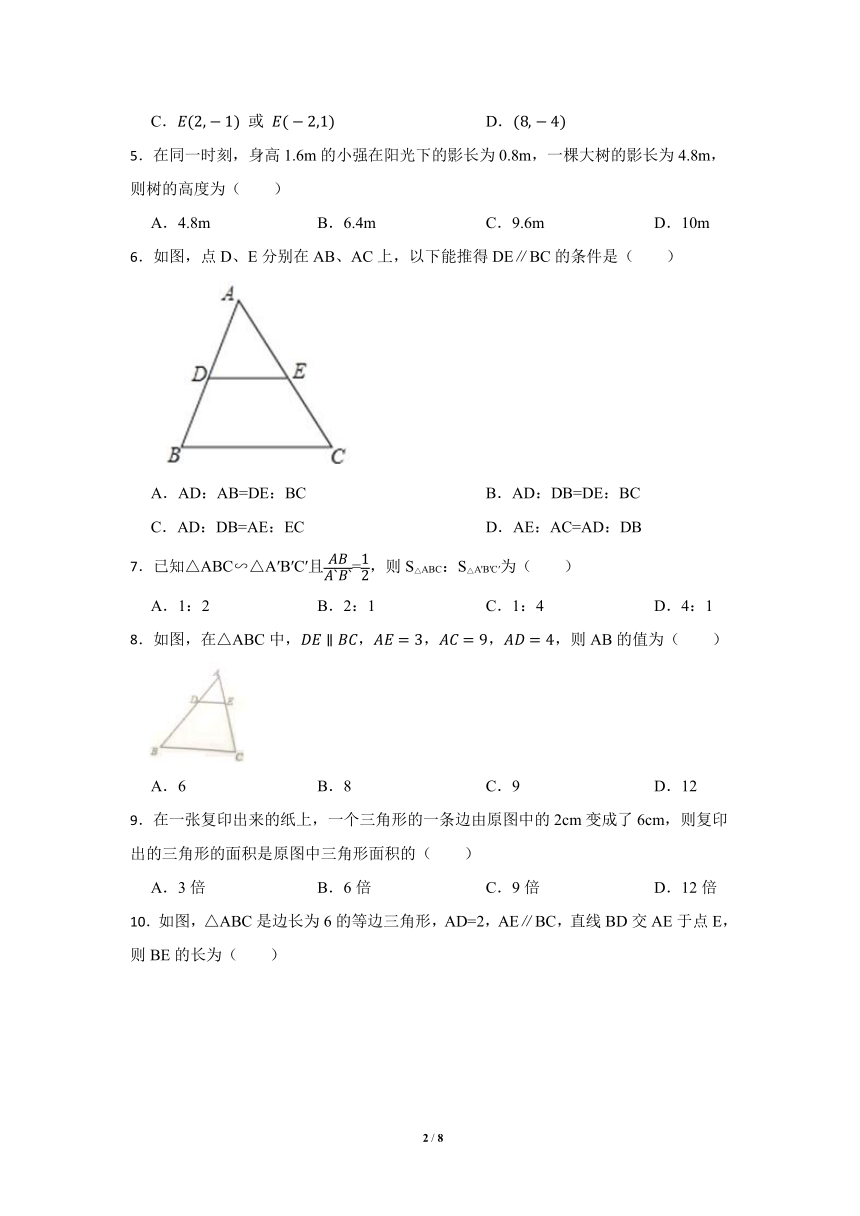
6.如图,点D、E分别在AB、AC上,以下能推得DE∥BC的条件是( )
A.AD:AB=DE:BC B.AD:DB=DE:BC
C.AD:DB=AE:EC D.AE:AC=AD:DB
7.已知△ABC∽△A′B′C′且=,则S△ABC:S△A'B'C′为( )
A.1:2 B.2:1 C.1:4 D.4:1
8.如图,在△ABC中,,,,,则AB的值为( )
A.6 B.8 C.9 D.12
9.在一张复印出来的纸上,一个三角形的一条边由原图中的2cm变成了6cm,则复印出的三角形的面积是原图中三角形面积的( )
A.3倍 B.6倍 C.9倍 D.12倍
10.如图,△ABC是边长为6的等边三角形,AD=2,AE∥BC,直线BD交AE于点E,则BE的长为( )
A.3 B.4 C.3 D.5
二、填空题
11.若 = = ,则 = .
12.若 ADE∽ ACB,且 ,DE=10,则BC= .
13.如图, ,AD=10,BD=8, 与 相似,则CD=
14.如图,是小林设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD,且测得AB=1.4米,BP=2.1米,PD=12米,那么该古城墙CD的高度是 米.
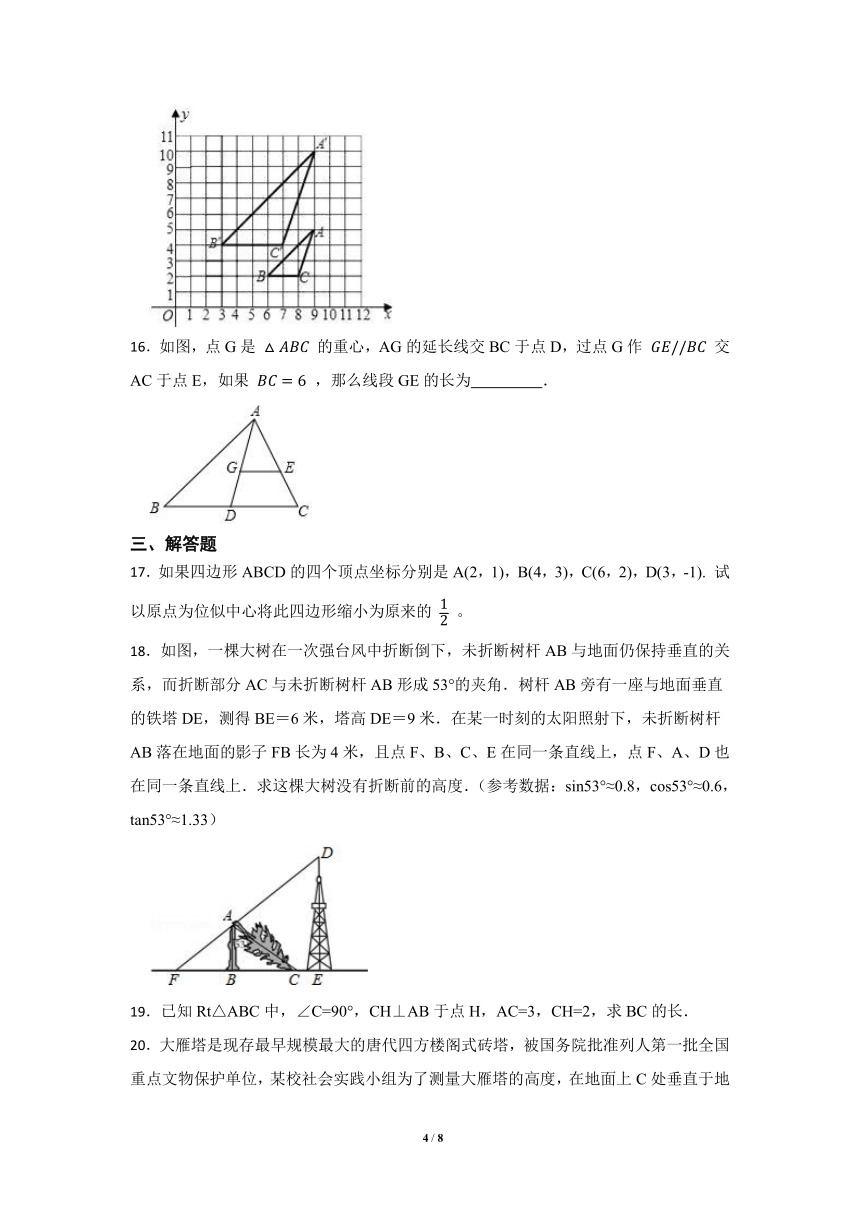
15.如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是 .
16.如图,点G是 的重心,AG的延长线交BC于点D,过点G作 交AC于点E,如果 ,那么线段GE的长为 .
三、解答题
17.如果四边形ABCD的四个顶点坐标分别是A(2,1),B(4,3),C(6,2),D(3,-1). 试以原点为位似中心将此四边形缩小为原来的 。
18.如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)
19.已知Rt△ABC中,∠C=90°,CH⊥AB于点H,AC=3,CH=2,求BC的长.
20.大雁塔是现存最早规模最大的唐代四方楼阁式砖塔,被国务院批准列人第一批全国重点文物保护单位,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为 米的标杆 ,这时地面上的点E,标杆的顶端点D,古塔的塔尖点B正好在同一直线上,测得 米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上) ,这时测得 米, 米,请你根据以上数据,计算古塔的高度 .
答案解析部分
1.B
2.D
3.C
4.C
5.C
6.C
7.C
8.D
9.C
10.A
11.
12.15
13.6.4或4.8
14.8
15.(9,0)
16.2
17.解:如图所示:
四边形A′B′C′D′即为所求.
18.解:∵AB⊥EF,DE⊥EF,
∴∠ABC=90°,AB∥DE,
∴△FAB∽△FDE,
∴ = ,
∵FB=4米,BE=6米,DE=9米,
∴ = ,得AB=3.6米,
∵∠ABC=90°,∠BAC=53°,cos∠BAC= ,
∴AC= = =6米,
∴AB+AC=3.6+6=9.6米,
即这棵大树没有折断前的高度是9.6米
19.解:∵Rt△ABC中,∠C=90°,CH⊥AB于点H,AC=3,CH=2,
∴AH2=AC2﹣CH2=5.
∴AH=.
又∵CH2=AH BH,
∴BH== ,
∴BC2=BH AB=×(+)= ,则BC=.
20.解:∵CD//AB,HG//AB,
∴△EDC∽△EBA,△FHG∽△FBA,
∴ ,
∵
∴ ,即
∴ (米),
∵ ,
∴ ,
∴AB=64.5.
答:古塔的高度 为64.5米.
7 / 8
第27章
班级________ 姓名________
一、单选题
1.如图,将图形用放大镜放大,这种图形的变化属于( )
A.平移 B.相似 C.旋转 D.对称
2.下列命题中,正确的是( )
A.如果一条直线截三角形两边的延长线所得的对应线段成比例,那么这条直线一定平行于三角形的第三边;
B.不同向量的单位向量的长度都相等,方向也都相同;
C.相似三角形的中线的比等于相似比;
D.一般来说,一条线段的黄金分割点有两个.
3.一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边是21,则其它两边的和是( ).
A.19 B.17 C.24 D.21
4.如图,已知 , ,以O为位似中心,把 缩小到原来的 ,则点E的对应点的坐标为是( )
A. B. 或
C. 或 D.
5.在同一时刻,身高1.6m的小强在阳光下的影长为0.8m,一棵大树的影长为4.8m,则树的高度为( )
A.4.8m B.6.4m C.9.6m D.10m
6.如图,点D、E分别在AB、AC上,以下能推得DE∥BC的条件是( )
A.AD:AB=DE:BC B.AD:DB=DE:BC
C.AD:DB=AE:EC D.AE:AC=AD:DB
7.已知△ABC∽△A′B′C′且=,则S△ABC:S△A'B'C′为( )
A.1:2 B.2:1 C.1:4 D.4:1
8.如图,在△ABC中,,,,,则AB的值为( )
A.6 B.8 C.9 D.12
9.在一张复印出来的纸上,一个三角形的一条边由原图中的2cm变成了6cm,则复印出的三角形的面积是原图中三角形面积的( )
A.3倍 B.6倍 C.9倍 D.12倍
10.如图,△ABC是边长为6的等边三角形,AD=2,AE∥BC,直线BD交AE于点E,则BE的长为( )
A.3 B.4 C.3 D.5
二、填空题
11.若 = = ,则 = .
12.若 ADE∽ ACB,且 ,DE=10,则BC= .
13.如图, ,AD=10,BD=8, 与 相似,则CD=
14.如图,是小林设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD,且测得AB=1.4米,BP=2.1米,PD=12米,那么该古城墙CD的高度是 米.
15.如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是 .
16.如图,点G是 的重心,AG的延长线交BC于点D,过点G作 交AC于点E,如果 ,那么线段GE的长为 .
三、解答题
17.如果四边形ABCD的四个顶点坐标分别是A(2,1),B(4,3),C(6,2),D(3,-1). 试以原点为位似中心将此四边形缩小为原来的 。
18.如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)
19.已知Rt△ABC中,∠C=90°,CH⊥AB于点H,AC=3,CH=2,求BC的长.
20.大雁塔是现存最早规模最大的唐代四方楼阁式砖塔,被国务院批准列人第一批全国重点文物保护单位,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为 米的标杆 ,这时地面上的点E,标杆的顶端点D,古塔的塔尖点B正好在同一直线上,测得 米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上) ,这时测得 米, 米,请你根据以上数据,计算古塔的高度 .
答案解析部分
1.B
2.D
3.C
4.C
5.C
6.C
7.C
8.D
9.C
10.A
11.
12.15
13.6.4或4.8
14.8
15.(9,0)
16.2
17.解:如图所示:
四边形A′B′C′D′即为所求.
18.解:∵AB⊥EF,DE⊥EF,
∴∠ABC=90°,AB∥DE,
∴△FAB∽△FDE,
∴ = ,
∵FB=4米,BE=6米,DE=9米,
∴ = ,得AB=3.6米,
∵∠ABC=90°,∠BAC=53°,cos∠BAC= ,
∴AC= = =6米,
∴AB+AC=3.6+6=9.6米,
即这棵大树没有折断前的高度是9.6米
19.解:∵Rt△ABC中,∠C=90°,CH⊥AB于点H,AC=3,CH=2,
∴AH2=AC2﹣CH2=5.
∴AH=.
又∵CH2=AH BH,
∴BH== ,
∴BC2=BH AB=×(+)= ,则BC=.
20.解:∵CD//AB,HG//AB,
∴△EDC∽△EBA,△FHG∽△FBA,
∴ ,
∵
∴ ,即
∴ (米),
∵ ,
∴ ,
∴AB=64.5.
答:古塔的高度 为64.5米.
7 / 8
