一元二次方程的应用2

课件22张PPT。一元二次方程的应用一元二次方程的应用（二） -----------面积问题 利率问题 授 课 人: 黄 敏
1.解一元二次方程有哪些方法？ 直接开平方法、配方法、公式法、因式分解法．
2.解方程
(80－2x)(60－2x)＝1500
(80－2x)(60－2x)＝1500 解(1)先把方程化为一元二次方程的一般形式 x2－70x＋825＝0．
(2)确认a,b,c的值 a＝1，b＝－70，c＝825
(3)判断b2－4ac的值
b2－4ac＝702－4×1×825＝1600＞0，
(4)代入求根公式得x1＝55，x2＝15 3.列一元一次方程方程解应用题的步骤？
①审题，
②找等量关系
③列方程，
④解方程，
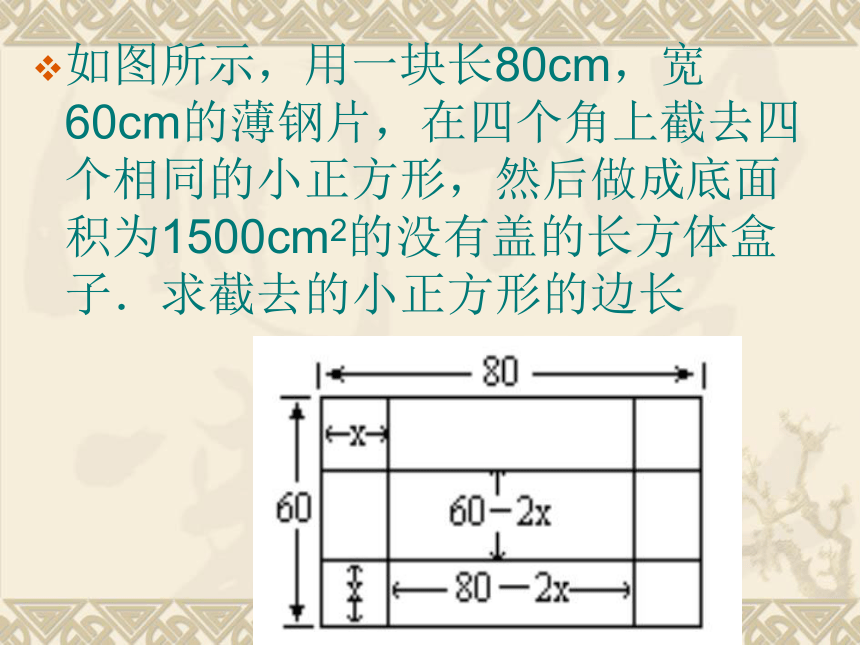
⑤答。 如图所示，用一块长80cm，宽60cm的薄钢片，在四个角上截去四个相同的小正方形，然后做成底面积为1500cm2的没有盖的长方体盒子．求截去的小正方形的边长 解：设截去的小正方形的边长xcm.则长和宽分别为(80－2x)cm、(60－2x)cm (80－2x)(60－2x)＝1500得x1＝55，x2＝15检验：当x1＝55时 长为80－2x＝-30cm
宽为60－2x＝-50cm． 想想，这符合题意吗？不符合． 舍去． 当x2＝15时 长为80－2x＝50cm
宽为60－2x＝30cm． 符合题意 所以只能取x＝15． 答：截取的小正方形的边长是15cm 列一元二次方程解应用题的步骤与列一元一次方程解应用题的步骤类似，即审、找、列、解、答．这里要特别注意．在列一元二次方程解应用题时，由于所得的根一般有两个，所以要检验这两个根是否符合实际问题的要求． 试一试：
如图，小明把一张边长为10cm的正方形硬纸板的四周剪去一个同样大小的正方形，再折合成一个无盖的长方形盒子。如果要求长方体的底面面积为81cm2，那么剪去的正方形边长为多少？边长2＝面积 解：设剪去的正方形的边长为 x cm，则长方体的底面边长为___________，依题意得：
(10－2x)2＝81
10－2x＝±9
∴x1＝ x2＝(10－2x)cm(不合题意，舍去)答：剪去的正方形的边长为0.5cm。（2）底面的长和宽能否用含x的代数式表示？ （3）你能找出题中的等量关系吗？你怎样列方程？
（1）若设纸盒的高为xcm，那么裁去的四个正方形
的边长为多少？想一想 如图1有一张长40cm，宽25cm的长方形硬纸片，
裁去角上四个小正方形之后，折成如图2那样的
无盖纸盒，若纸盒的底面积是450cm2，那么纸
盒的高是多少？ 40-2x练习：一块长方形铁板，长是宽的2倍，如果在4个角上截去边长为5cm的小正方形，? 然后把四边折起来，做成一个没有盖的盒子，盒子的容积是3000 cm3，求铁板的长和宽． 解：设铁板的宽为xcm,则有长为2xcm5(2x-10)(x-10)=3000例：一种铁栅栏护窗的正面为120cm、宽为100cm的矩形，在中间有一个由4根铁条组成的菱形，如图，菱形的水平方向的对角线比竖直方向的对角线长20cm，并且菱形的面积是护窗正面矩形面积的 。
(1)求菱形的两条对角线的长度；
(2)求组成菱形的每一根铁条的长度练习二：如图，在一块长为92m，宽为60m的矩形耕地上挖三条水渠，水渠的宽都相等，水渠把耕地分成面积均为885m2的6个矩形小块，水渠应挖多宽？ 解：设水渠应挖 x m宽，则矩形小块的长为 m，宽为 m，依题意得：化为一般形式：x2－106x＋105＝0
(x－1)(x－105)＝0
∴x1＝1，x2＝105(不合题意，舍去)答：水渠应挖 1 m宽。例题:某药品两次升价，零售价升为原来的 1.2倍，已知两次升价的百分率一样，求每次升价的百分率（精确到0.1%）解，设原价为 元，每次升价的百分率为 ，
根据题意，得 解这个方程，得 由于升价的百分率不可能是负数，
所以 不合题意，舍去答：每次升价的百分率为9.5%. 变换题1：某药品经两次降价，零售价降为原来的一半.已知两次降价的百分率一样，求每次降价的百分率.（精确到0.1%） 解：设原价为1个单位，
每次降价的百分率为 x.
根据题意，得 解这个方程，得 答：每次降价的百分率为29.3%. 问题2某商店6月份的利润是2500元，要使8月份的利润达到3600元，这两个月的利润平均月增长的百分率是多少？某民营企业成立3年来，累计向国家上缴利税280万元，其中第一年上缴40万元，求上缴利税的年平均增长率。 某商场销售一批名牌衬衫，平均每天可售出20件，每件赢利40元。为了扩大销售，增加利润，商场决定采取适当降价措施。经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件。（1）若商场平均每天要赢利1200元，则每件衬衫应降价多少元？为尽快减少库存，以便资金周转，则降价多少元？（2）能不能通过适当的降价，使商场的每天衬衫销售获利达到最大？若能，则降价多少元？最大获利是多少元？(小组合作探究)练习1练习2：如图,在一幅长90cm,宽40cm的风景画四周镶上一条宽度相同的金色纸边,制成一幅挂画.如果要求风景画的面积是整个面积的72%,那么金边的宽应是多少? 已知矩形(记为A)长为4，宽为1，是否存在另一个矩形(记为B),使得这个矩形的周长和面积都为原来矩形周长和面积的一半?如果存在,求出这个矩形的长和宽；如果不存在,试说明理由。探究活动