人教版数学九年级下册 28.1锐角三角函数 学案(含答案)
文档属性
| 名称 | 人教版数学九年级下册 28.1锐角三角函数 学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 210.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 00:00:00 | ||
图片预览



文档简介
三角函数定义----拓展
班级: 姓名: 组号:
一、巩固训练
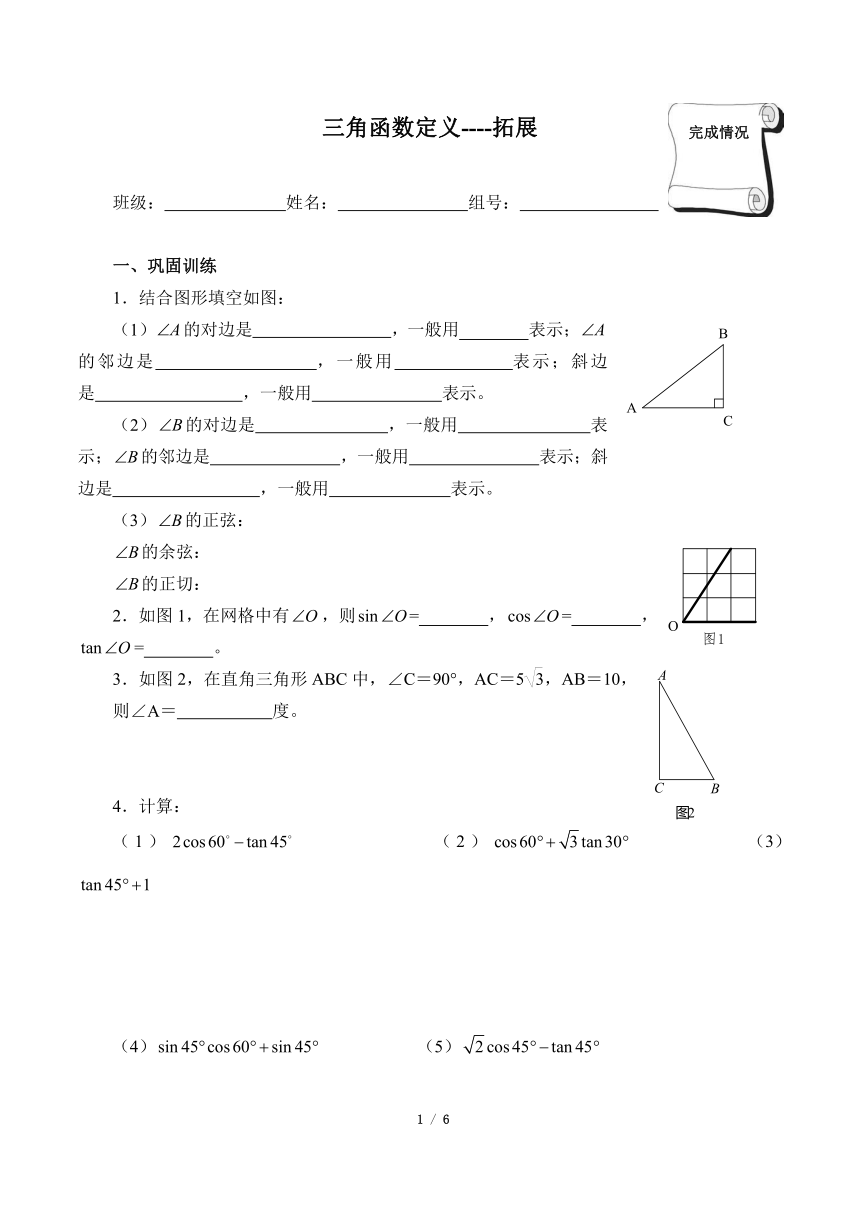
1.结合图形填空如图:
(1)的对边是 ,一般用 表示;的邻边是 ,一般用 表示;斜边是 ,一般用 表示。
(2)的对边是 ,一般用 表示;的邻边是 ,一般用 表示;斜边是 ,一般用 表示。
(3)的正弦:
的余弦:
的正切:
2.如图1,在网格中有,则= ,= ,= 。
3.如图2,在直角三角形ABC中,∠C=90°,AC=5,AB=10,
则∠A= 度。
4.计算:
(1) (2) (3)
(4) (5)
(6)
二、错题再现
1.如图3,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.已知AC=,BC=2,那么sin∠ACD=( )
A. B. C. D.
2.设α、β均为锐角,且,则= °
3.若,则△ABC( )。
A.是直角三角形 B.是等边三角形
C.是含有60°的任意三角形 D.是顶角为钝角的等腰三角形
三、能力提升
1.已知:如图4,在△ABC中,∠C=90°,点D.E分别在边AB、AC上,DE∥BC,DE=3,BC=9。
(1)求 的值;
(2)若BD=10,求sin∠A的值。
2.已知锐角三角形ABC,点D在BC的延长线上,连接AD,若∠DAB=90°,∠ACB=2∠D,AD=2,AC=,根据题意画出示意图,并求tanD的值。
四、精练反馈
A组
1.在△ABC中,若∠C=90°,AC=1,AB=5,则sinB=
2.计算:
(1) (2)
B组
3.已知是锐角,且,求的值。
【答案】
巩固训练
1.(1)BC,AC,b,AB,c
(2)AC;b;BC;a;AB;c
(3)
2.,,
3.30
4.
错题再现
1.A 2.90° 3.A
能力提升
1.(1)解:(1)DE∥BC,∴△ADE ∽△ABC,∴,∴;
(2)∵,BD =10 ,∴,∴AD=5,
经检验,符合题意,∴AB=15,
在Rt△ABC 中,sin∠A=。
2.
解:如图
∵∠ACB=∠D+∠CAD,∠ACB=2∠D,
∴∠CAD=∠D
∴ CA=CD∵∠BAD=90°,
∴∠B+∠D=90°,∵∠BAC+∠CAD=90°,∴∠B=∠BAC
∴CB=CA ∴BD =2AC
∵AC=, ∴BD=3.
在Rt△BAD中,∵AD=2,∴AB=
∴tanD==
精练反馈
1.
2.
(1)
(2)
3.
解:a是锐角,a+15°∈(15°,105°)sin(a+15°)=
a+15°=60°a=45°
原式=-4cos45°-1+tan45°+3
=-4-1 + 1 + 3
=2-2+3
=3
1 / 6
班级: 姓名: 组号:
一、巩固训练
1.结合图形填空如图:
(1)的对边是 ,一般用 表示;的邻边是 ,一般用 表示;斜边是 ,一般用 表示。
(2)的对边是 ,一般用 表示;的邻边是 ,一般用 表示;斜边是 ,一般用 表示。
(3)的正弦:
的余弦:
的正切:
2.如图1,在网格中有,则= ,= ,= 。
3.如图2,在直角三角形ABC中,∠C=90°,AC=5,AB=10,
则∠A= 度。
4.计算:
(1) (2) (3)
(4) (5)
(6)
二、错题再现
1.如图3,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.已知AC=,BC=2,那么sin∠ACD=( )
A. B. C. D.
2.设α、β均为锐角,且,则= °
3.若,则△ABC( )。
A.是直角三角形 B.是等边三角形
C.是含有60°的任意三角形 D.是顶角为钝角的等腰三角形
三、能力提升
1.已知:如图4,在△ABC中,∠C=90°,点D.E分别在边AB、AC上,DE∥BC,DE=3,BC=9。
(1)求 的值;
(2)若BD=10,求sin∠A的值。
2.已知锐角三角形ABC,点D在BC的延长线上,连接AD,若∠DAB=90°,∠ACB=2∠D,AD=2,AC=,根据题意画出示意图,并求tanD的值。
四、精练反馈
A组
1.在△ABC中,若∠C=90°,AC=1,AB=5,则sinB=
2.计算:
(1) (2)
B组
3.已知是锐角,且,求的值。
【答案】
巩固训练
1.(1)BC,AC,b,AB,c
(2)AC;b;BC;a;AB;c
(3)
2.,,
3.30
4.
错题再现
1.A 2.90° 3.A
能力提升
1.(1)解:(1)DE∥BC,∴△ADE ∽△ABC,∴,∴;
(2)∵,BD =10 ,∴,∴AD=5,
经检验,符合题意,∴AB=15,
在Rt△ABC 中,sin∠A=。
2.
解:如图
∵∠ACB=∠D+∠CAD,∠ACB=2∠D,
∴∠CAD=∠D
∴ CA=CD∵∠BAD=90°,
∴∠B+∠D=90°,∵∠BAC+∠CAD=90°,∴∠B=∠BAC
∴CB=CA ∴BD =2AC
∵AC=, ∴BD=3.
在Rt△BAD中,∵AD=2,∴AB=
∴tanD==
精练反馈
1.
2.
(1)
(2)
3.
解:a是锐角,a+15°∈(15°,105°)sin(a+15°)=
a+15°=60°a=45°
原式=-4cos45°-1+tan45°+3
=-4-1 + 1 + 3
=2-2+3
=3
1 / 6
