12.1轴对称(2)(山东省济宁市微山县)
文档属性
| 名称 | 12.1轴对称(2)(山东省济宁市微山县) |

|
|
| 格式 | rar | ||
| 文件大小 | 533.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-24 00:00:00 | ||
图片预览


文档简介
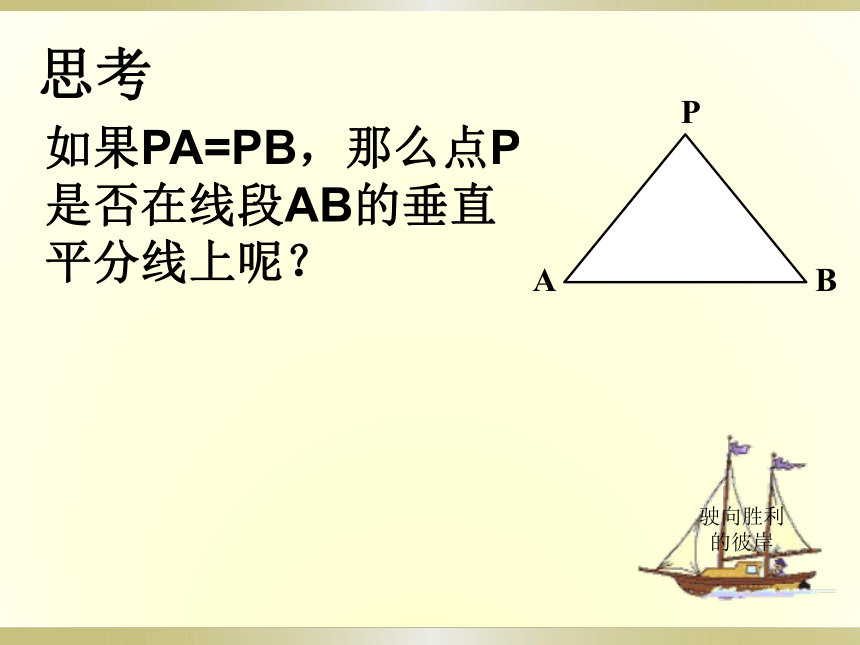
课件13张PPT。12.1轴对称(3)主讲 金启国思考如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?驶向胜利的彼岸ABP用一根木棒和一根弹性均匀的橡皮筋,做一 个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保持射出去的方向与木棒垂直呢?为什么?
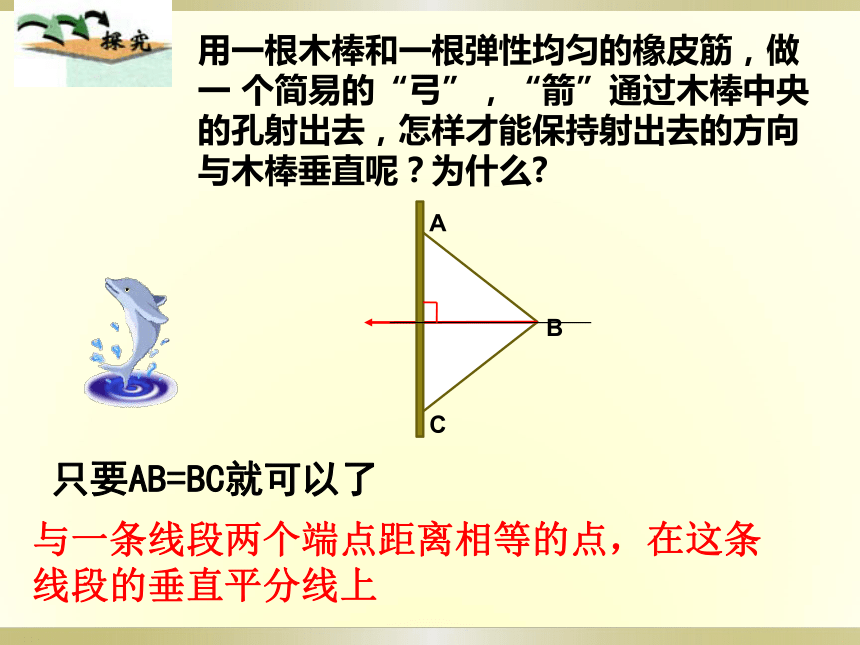
CBA只要AB=BC就可以了与一条线段两个端点距离相等的点,在这条线段的垂直平分线上与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
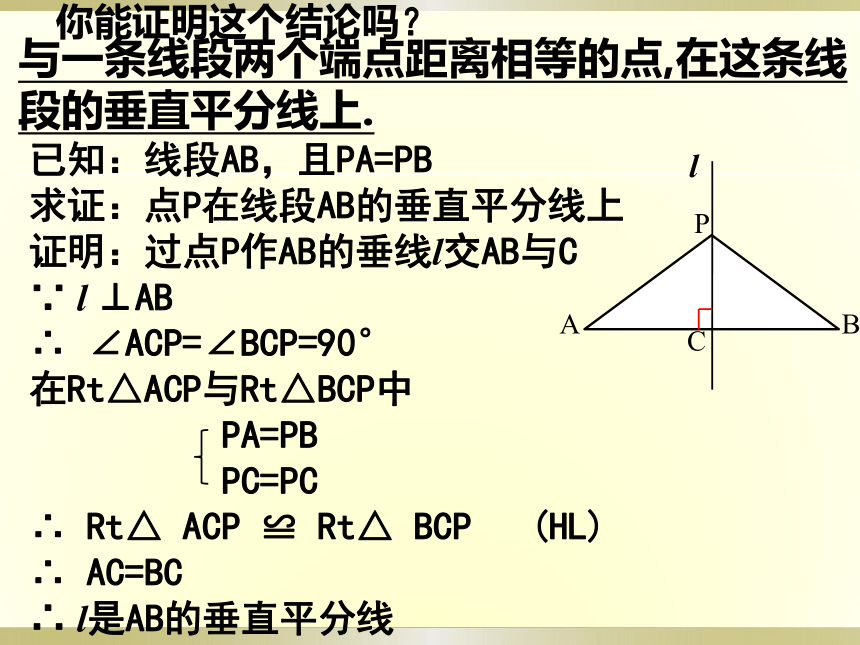
你能证明这个结论吗?ABCP l 已知:线段AB,且PA=PB
求证:点P在线段AB的垂直平分线上
证明:过点P作AB的垂线l交AB与C
∵ l ⊥AB
∴ ∠ACP=∠BCP=90°
在Rt△ACP与Rt△BCP中
PA=PB
PC=PC
∴ Rt△ ACP ≌ Rt△ BCP (HL)
∴ AC=BC
∴ l是AB的垂直平分线
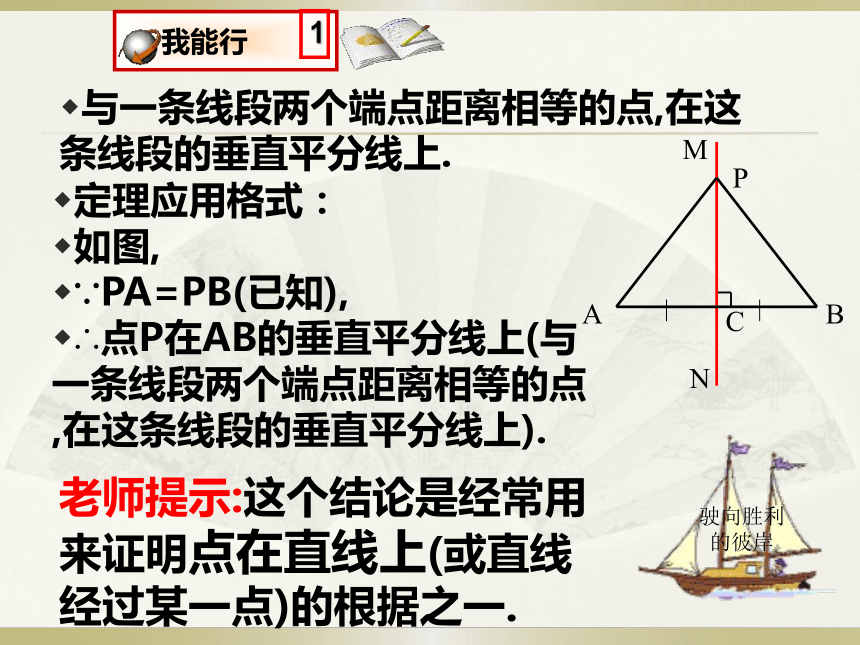
驶向胜利的彼岸与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.定理应用格式:
如图,
∵PA=PB(已知),
∴点P在AB的垂直平分线上(与一条线段两个端点距离相等的点,在这条线段的垂直平分线上).老师提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.结论:在线段AB的垂直平分线l上的点与A,B的距离都相等;反过来,与两点A,B的距离相等的点都在l上,所以直线l可以看成与两点A,B的距离相等的所有点的集合.练习
1.如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?MABCM分析:因为AB=AC,所以A在BC的垂直
平分线上
同理M也在BC的垂直平分线上,
而BC的垂直平分线只有一条,
由两点决定一条直线,
AM是BC的垂直平分线拓展:如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长。证明:
∵N在MN的垂直平分线上
∴ BN=AN
∴ △BCN的周长=BN+NC+BC
=AN+NC+BC=AC+BC=32+21=53已知: △ABC中,边AB、 BC的垂直平分线交于点P。 (1)求证:PA=PB=PC. (2)点P是否也在边AC的垂直平分线 上呢?由此你还能得出什么结论?结论:三角形三边的垂直平分线交于一点,并且这点到三个顶点的距离相等。——重心ABCP(1)证明:由题意可知点P在AB的垂直平分线上
∵ PA=PB
同理可得PB=PC
∴ PA=PB=PC
(2)由(1)知PA=PC
∴ P在AC的垂直平分线上(与一条线段两个端点距离相等
的点,在这条线段的垂直平分线上).
例 : 如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗?⑴分别以点A、B为圆心,以大于 AB的长为半径作弧,两弧相交于C、D两点;
⑵作直线CD
CD即为所求的直线。CD 如图,七(1)班与七(2)班两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且PM=PN,请你用折纸的方法找出P点并说明理由。?MNBCA做一做P小结:通过本节课你有哪些收获?
CBA只要AB=BC就可以了与一条线段两个端点距离相等的点,在这条线段的垂直平分线上与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
你能证明这个结论吗?ABCP l 已知:线段AB,且PA=PB
求证:点P在线段AB的垂直平分线上
证明:过点P作AB的垂线l交AB与C
∵ l ⊥AB
∴ ∠ACP=∠BCP=90°
在Rt△ACP与Rt△BCP中
PA=PB
PC=PC
∴ Rt△ ACP ≌ Rt△ BCP (HL)
∴ AC=BC
∴ l是AB的垂直平分线
驶向胜利的彼岸与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.定理应用格式:
如图,
∵PA=PB(已知),
∴点P在AB的垂直平分线上(与一条线段两个端点距离相等的点,在这条线段的垂直平分线上).老师提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.结论:在线段AB的垂直平分线l上的点与A,B的距离都相等;反过来,与两点A,B的距离相等的点都在l上,所以直线l可以看成与两点A,B的距离相等的所有点的集合.练习
1.如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?MABCM分析:因为AB=AC,所以A在BC的垂直
平分线上
同理M也在BC的垂直平分线上,
而BC的垂直平分线只有一条,
由两点决定一条直线,
AM是BC的垂直平分线拓展:如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长。证明:
∵N在MN的垂直平分线上
∴ BN=AN
∴ △BCN的周长=BN+NC+BC
=AN+NC+BC=AC+BC=32+21=53已知: △ABC中,边AB、 BC的垂直平分线交于点P。 (1)求证:PA=PB=PC. (2)点P是否也在边AC的垂直平分线 上呢?由此你还能得出什么结论?结论:三角形三边的垂直平分线交于一点,并且这点到三个顶点的距离相等。——重心ABCP(1)证明:由题意可知点P在AB的垂直平分线上
∵ PA=PB
同理可得PB=PC
∴ PA=PB=PC
(2)由(1)知PA=PC
∴ P在AC的垂直平分线上(与一条线段两个端点距离相等
的点,在这条线段的垂直平分线上).
例 : 如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗?⑴分别以点A、B为圆心,以大于 AB的长为半径作弧,两弧相交于C、D两点;
⑵作直线CD
CD即为所求的直线。CD 如图,七(1)班与七(2)班两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且PM=PN,请你用折纸的方法找出P点并说明理由。?MNBCA做一做P小结:通过本节课你有哪些收获?
