苏科版八年级数学下册 11.3用反比例函数解决问题--k值问题 试题(含答案)
文档属性
| 名称 | 苏科版八年级数学下册 11.3用反比例函数解决问题--k值问题 试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 150.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 13:11:59 | ||
图片预览



文档简介
11.3用反比例函数解决问题--k值问题
一、选择题.
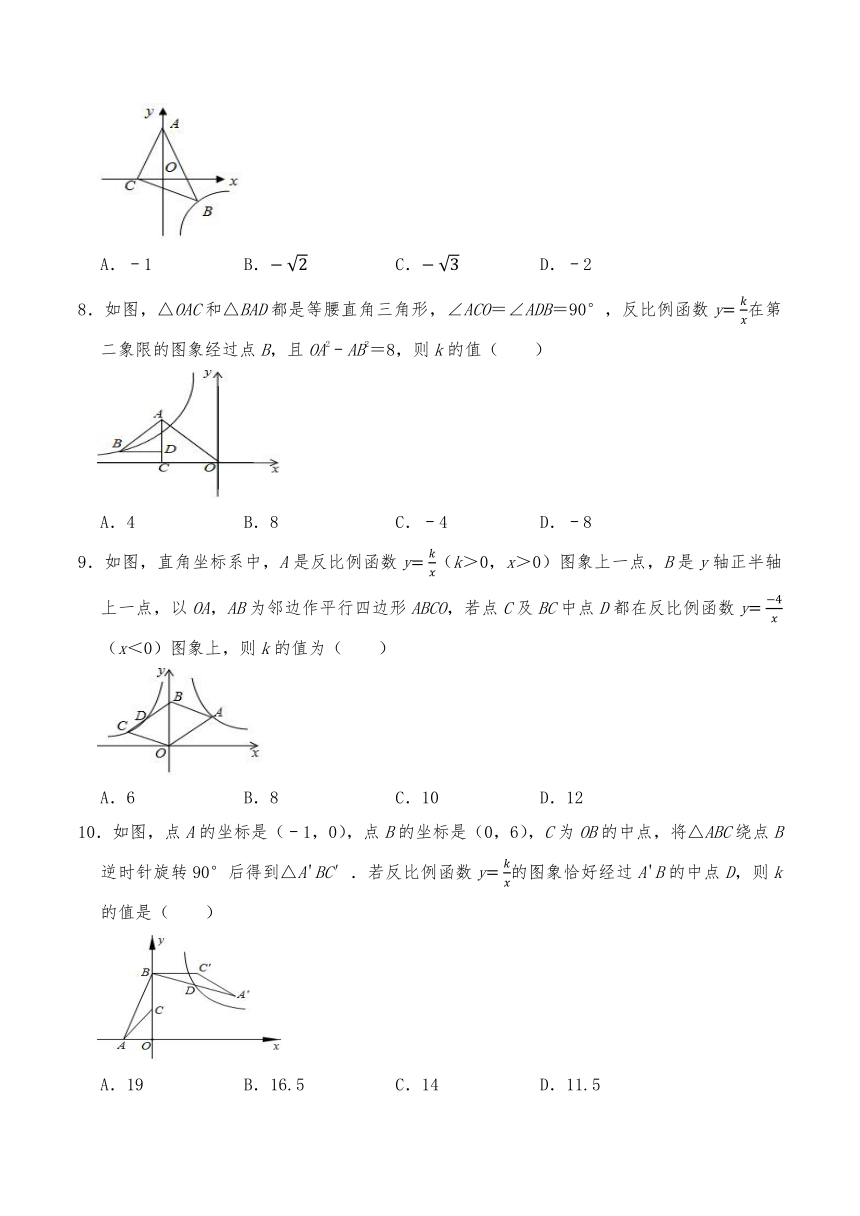
1.如图,已知在平面直角坐标系中,Rt△ABC的顶点A(0,3),B(3,0),∠ABC=90°.函数y(x>0)的图象经过点C,则AC的长为( )
A.3 B.2 C.2 D.
2.如图,反比例函数的图象经过平行四边形ABCD的顶点C,D,若点A、点B、点C的坐标分别为(3,0),(0,4),(a,b),且a+b=7.5,则k的值是( )
A.7.5 B.9 C.10 D.12
3.如图,矩形OABC的一个顶点与坐标原点重合,OC、OA分别在x轴和y轴上,正方形CDEF的一条边在x轴上,另一条边CD在BC上,反比例函数y的图象经过B、E两点,已知OA=5,则正方形的边长是( )
A.42 B.4﹣2 C.22 D.
4.如图,在平面直角坐标系中,正方形ABCD的顶点A、D分别在x轴、y轴上,反比例函数y(k>0,x>0)的图象经过正方形对角线的交点E,若点A(2,0)、D(0,4),则k=( )
A.6 B.8 C.9 D.12
5.如图,在平面直角坐标系中,A是反比例函数y(k>0,x>0)图象上一点,B是y轴正半轴上一点,以OA、AB为邻边作 ABCO.若点C及BC中点D都在反比例函数y(x<0)图象上,则k的值为( )
A.6 B.8 C.10 D.12
6.如图,A,B两点在反比例函数y的图象上,C,D两点在反比例函数y的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=6,BD=3,EF=8,则k1﹣k2的值是( )
A.10 B.18 C.12 D.16
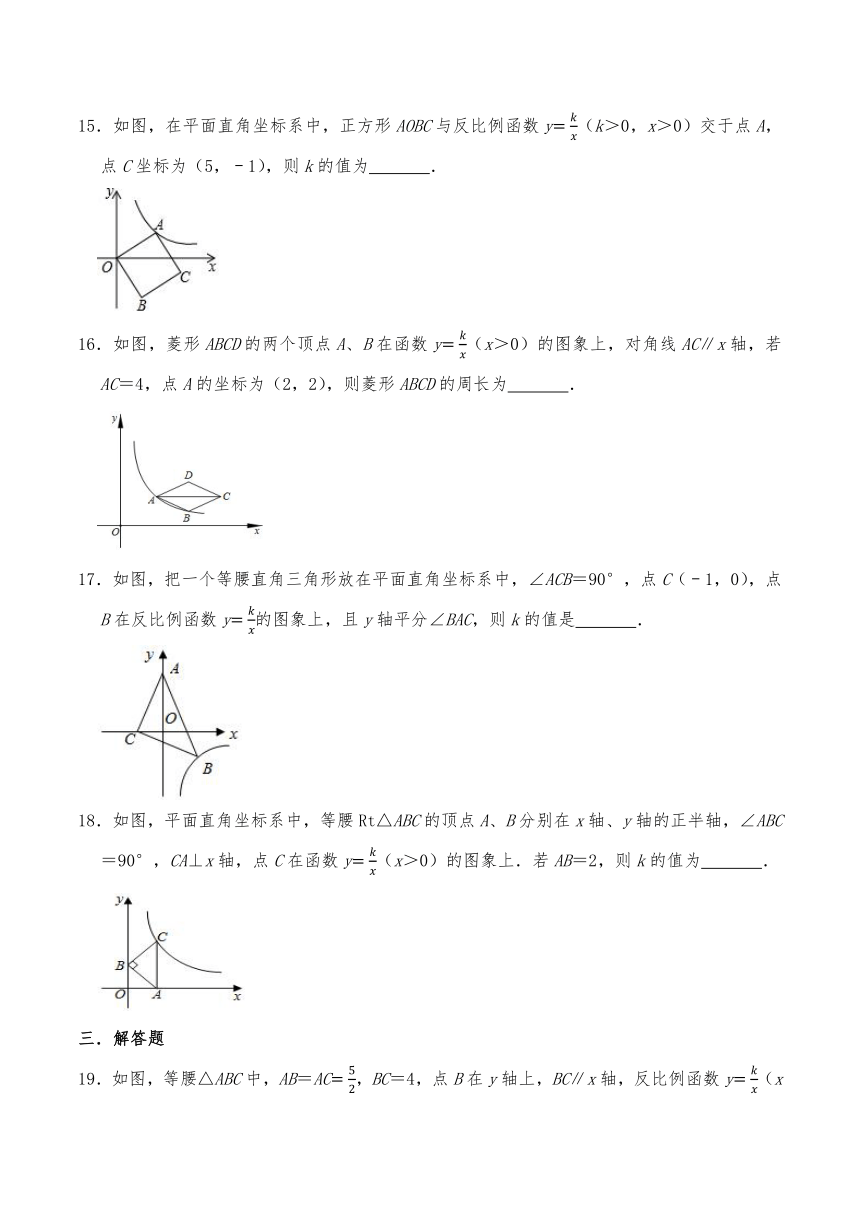
7.如图,把一个等腰直角三角形放在平面直角坐标系中,∠ACB=90°,点C(﹣1,0),点B在反比例函数y的图象上,且y轴平分∠BAC,则k的值是( )
A.﹣1 B. C. D.﹣2
8.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y在第二象限的图象经过点B,且OA2﹣AB2=8,则k的值( )
A.4 B.8 C.﹣4 D.﹣8
9.如图,直角坐标系中,A是反比例函数y(k>0,x>0)图象上一点,B是y轴正半轴上一点,以OA,AB为邻边作平行四边形ABCO,若点C及BC中点D都在反比例函数y(x<0)图象上,则k的值为( )
A.6 B.8 C.10 D.12
10.如图,点A的坐标是(﹣1,0),点B的坐标是(0,6),C为OB的中点,将△ABC绕点B逆时针旋转90°后得到△A'BC′.若反比例函数y的图象恰好经过A'B的中点D,则k的值是( )
A.19 B.16.5 C.14 D.11.5
二、填空题
11.如图,已知点A是反比例函数y图象上的一个动点,连接OA,若将线段OA绕点O逆时针旋转90°得到线段OB,则过点B的反比例函数解析式为 .
12.如图,已知平面直角坐标系中A点坐标为(0,3),以OA为一边在第一象限作三角形OAB.E为AB中点,OB=4.若反比例函数y的图象恰好经过点B和点E,则k的值为 .
13.如图,点D是矩形AOBC的对称中心,点A坐标是(0,2),点B的坐标是(4,0),反比例函数y(k≠0)的图象经过点D,则k= .
14.(秦淮区一模)如图,在平面直角坐标系中,等腰三角形ABC的腰AB经过原点,底边BC与x轴平行,反比例函数y的图象经过A、B两点,若点A的坐标为(1,4),则点C的坐标为 .
15.如图,在平面直角坐标系中,正方形AOBC与反比例函数y(k>0,x>0)交于点A,点C坐标为(5,﹣1),则k的值为 .
16.如图,菱形ABCD的两个顶点A、B在函数y(x>0)的图象上,对角线AC∥x轴,若AC=4,点A的坐标为(2,2),则菱形ABCD的周长为 .
17.如图,把一个等腰直角三角形放在平面直角坐标系中,∠ACB=90°,点C(﹣1,0),点B在反比例函数y的图象上,且y轴平分∠BAC,则k的值是 .
18.如图,平面直角坐标系中,等腰Rt△ABC的顶点A、B分别在x轴、y轴的正半轴,∠ABC=90°,CA⊥x轴,点C在函数y(x>0)的图象上.若AB=2,则k的值为 .
三.解答题
19.如图,等腰△ABC中,AB=AC,BC=4,点B在y轴上,BC∥x轴,反比例函数y(x>0)的图象经过点A,交BC于点D.
(1)若OB=3,求k的值;
(2)连接CO,若AB=BD,求四边形ABOC的周长.
20.如图,边长为2的正方形ABCD的顶点A,B在x轴正半轴上,反比例函数y在第一象限的图象经过点D,交BC于E.
(1)当点E的坐标为(3,n)时,求n和k的值;
(2)若点E是BC的中点,求OD的长.
21.如图,菱形OABC放置在第一象限内,顶点A在x轴上,若顶点B的坐标是(4,3).
(1)请求出菱形边长OA的长度.
(2)反比例函数y经过点C,请求出k的值.
22.如图,在△ABC中,AC=BC,AB⊥x轴于A,反比例函数y(x>0)的图象经过点C,交AB于点D,已知AB=4,BC.
(1)若OA=4,求k的值.
(2)连接OC,若AD=AC,求CO的长.
23.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y(x>0)的图象上,点D的坐标为(3,4).
(1)菱形ABCD的边长为 ;
(2)求k的值;
(3)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
24.如图, OABC的边OA在x轴的正半轴上,OA=5,反比例函数(x>0)的图象经过点C(1,4).
(1)求反比例函数的关系式和点B的坐标;
(2)过AB的中点D作DP∥x轴交反比例函数图象于点P,连接CP,OP.求△COP的面积.
答案
一、选择题.
B.B.C.C.B.D.B.C.B.B.
二、填空题
11.y.
12..
13.2.
14.(3,﹣4).
15.6.
16.4.
17..
18.4.
三.解答题
19.(1)过A作AE⊥BC于E交x轴于F,
则AF∥y轴,
∵BC∥x轴,
∴四边形BOFE是矩形,
∴EF=OB=3,
∵AB=AC,BC=4,
∴BEBC=2,
∴AE,
∴A(2,),
∵反比例函数y(x>0)的图象经过点A,
∴k=29;
(2)设OB=a,
∵BD=AB,
∴A(2,a),D(,a),
∵反比例函数y(x>0)的图象经过点A,交BC于点D,
∴2(a)a,
解得:a=6,
∴OB=6,
∴OC2,
∴四边形ABOC的周长=AB+OB+OC+AC=11+2.
20.(1)∵正方形ABCD的边长为2,点E的坐标为(3,n),
∴OB=3,AB=AD=2,
∴D(1,2),
∵反比例函数y在第一象限的图象经过点D,
∴k=1×2=2,
∴反比例为:y,
∵反比例函数y在第一象限的图象交BC于E,
∴n;
(2)设D(x,2)则E(x+2,1),
∵反比例函数y在第一象限的图象经过点D、点E,
∴2x=x+2,
解得x=2,
∴D(2,2),
∴OA=AD=2,
∴OD2.
21.(1)如图,过B作BD⊥x轴于D,则BD=3,OD=4,
设AO=x=AB,则AD=4﹣x,
∵Rt△ABD中,AD2+BD2=AB2,
∴(4﹣x)2+32=x2,
解得x,
∴菱形边长OA的长度为.
(2)如图,过C作CE⊥x轴于E,则四边形BCED是矩形,
∴BC=DE,CE=BD=3,
∴OE=OD﹣DE=4,
∴点C的坐标为(,3),
∵反比例函数y经过点C,
∴k.
22.(1)作CE⊥AB,垂足为E,
∵AC=BC,AB=4,
∴AE=BE=2.
在Rt△BCE中,BC,BE=2,
∴CE,
∵OA=4,
∴C点的坐标为:(,2),
∵点C在y(x>0)的图象上,
∴k=11;
(2)设A点的坐标为(m,0),
∵AC=BC,AD=AC,
∴AD,
∴D,C两点的坐标分别为:(m,),(m,2).
∵点C,D都在y(x>0)的图象上,
∴m=2(m),
∴m=6,
∴C点的坐标为:(,2),
作CF⊥x轴,垂足为F,
∴OF,CF=2,
在Rt△OFC中,
OC2=OF2+CF2,
∴OC.
23.(1)∵点D的坐标为(3,4),
∴由勾股定理得:OD5,
即菱形ABCD的边长为5,
故答案为:5;
(2)∵菱形ABCD的边长为5,
∴OD=AD=5,AD∥OB,
∵D(3,4),
∴A的坐标为(3,9),
代入y得:k=27,
故答案为:27;
(3)将菱形ABCD沿x轴正方向平移,使得点D落在函数y(x>0)的图象D′点处,
过点D′做x轴的垂线,垂足为F′.
∵DF=4,
∴D′F′=4,
∴点D′的纵坐标为4,
∵点D′在y的图象上,
∴4,
解得:x,
即OF′,
∴FF′3,
∴菱形ABCD平移的距离为.
24.(1)∵反比例函数y(x>0)的图象经过点C(1,4).
∴m=1×4=4,
∴反比例函数的关系式为y(x>0).
∵四边形OABC为平行四边形,且点O(0,0),OA=5,点C(1,4),
∴点A(5,0),
∴点B(6,4).
(2)延长DP交OC于点E,如图所示.
∵点D为线段BA的中点,点A(5,0)、B(6,4),
∴点D(,2).
令y中y=2,则x=2,
∴点P(2,2),
∴PD2,EP=ED﹣PD,
∴S△COPEP (yC﹣yO)(4﹣0)=3.
一、选择题.
1.如图,已知在平面直角坐标系中,Rt△ABC的顶点A(0,3),B(3,0),∠ABC=90°.函数y(x>0)的图象经过点C,则AC的长为( )
A.3 B.2 C.2 D.
2.如图,反比例函数的图象经过平行四边形ABCD的顶点C,D,若点A、点B、点C的坐标分别为(3,0),(0,4),(a,b),且a+b=7.5,则k的值是( )
A.7.5 B.9 C.10 D.12
3.如图,矩形OABC的一个顶点与坐标原点重合,OC、OA分别在x轴和y轴上,正方形CDEF的一条边在x轴上,另一条边CD在BC上,反比例函数y的图象经过B、E两点,已知OA=5,则正方形的边长是( )
A.42 B.4﹣2 C.22 D.
4.如图,在平面直角坐标系中,正方形ABCD的顶点A、D分别在x轴、y轴上,反比例函数y(k>0,x>0)的图象经过正方形对角线的交点E,若点A(2,0)、D(0,4),则k=( )
A.6 B.8 C.9 D.12
5.如图,在平面直角坐标系中,A是反比例函数y(k>0,x>0)图象上一点,B是y轴正半轴上一点,以OA、AB为邻边作 ABCO.若点C及BC中点D都在反比例函数y(x<0)图象上,则k的值为( )
A.6 B.8 C.10 D.12
6.如图,A,B两点在反比例函数y的图象上,C,D两点在反比例函数y的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=6,BD=3,EF=8,则k1﹣k2的值是( )
A.10 B.18 C.12 D.16
7.如图,把一个等腰直角三角形放在平面直角坐标系中,∠ACB=90°,点C(﹣1,0),点B在反比例函数y的图象上,且y轴平分∠BAC,则k的值是( )
A.﹣1 B. C. D.﹣2
8.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y在第二象限的图象经过点B,且OA2﹣AB2=8,则k的值( )
A.4 B.8 C.﹣4 D.﹣8
9.如图,直角坐标系中,A是反比例函数y(k>0,x>0)图象上一点,B是y轴正半轴上一点,以OA,AB为邻边作平行四边形ABCO,若点C及BC中点D都在反比例函数y(x<0)图象上,则k的值为( )
A.6 B.8 C.10 D.12
10.如图,点A的坐标是(﹣1,0),点B的坐标是(0,6),C为OB的中点,将△ABC绕点B逆时针旋转90°后得到△A'BC′.若反比例函数y的图象恰好经过A'B的中点D,则k的值是( )
A.19 B.16.5 C.14 D.11.5
二、填空题
11.如图,已知点A是反比例函数y图象上的一个动点,连接OA,若将线段OA绕点O逆时针旋转90°得到线段OB,则过点B的反比例函数解析式为 .
12.如图,已知平面直角坐标系中A点坐标为(0,3),以OA为一边在第一象限作三角形OAB.E为AB中点,OB=4.若反比例函数y的图象恰好经过点B和点E,则k的值为 .
13.如图,点D是矩形AOBC的对称中心,点A坐标是(0,2),点B的坐标是(4,0),反比例函数y(k≠0)的图象经过点D,则k= .
14.(秦淮区一模)如图,在平面直角坐标系中,等腰三角形ABC的腰AB经过原点,底边BC与x轴平行,反比例函数y的图象经过A、B两点,若点A的坐标为(1,4),则点C的坐标为 .
15.如图,在平面直角坐标系中,正方形AOBC与反比例函数y(k>0,x>0)交于点A,点C坐标为(5,﹣1),则k的值为 .
16.如图,菱形ABCD的两个顶点A、B在函数y(x>0)的图象上,对角线AC∥x轴,若AC=4,点A的坐标为(2,2),则菱形ABCD的周长为 .
17.如图,把一个等腰直角三角形放在平面直角坐标系中,∠ACB=90°,点C(﹣1,0),点B在反比例函数y的图象上,且y轴平分∠BAC,则k的值是 .
18.如图,平面直角坐标系中,等腰Rt△ABC的顶点A、B分别在x轴、y轴的正半轴,∠ABC=90°,CA⊥x轴,点C在函数y(x>0)的图象上.若AB=2,则k的值为 .
三.解答题
19.如图,等腰△ABC中,AB=AC,BC=4,点B在y轴上,BC∥x轴,反比例函数y(x>0)的图象经过点A,交BC于点D.
(1)若OB=3,求k的值;
(2)连接CO,若AB=BD,求四边形ABOC的周长.
20.如图,边长为2的正方形ABCD的顶点A,B在x轴正半轴上,反比例函数y在第一象限的图象经过点D,交BC于E.
(1)当点E的坐标为(3,n)时,求n和k的值;
(2)若点E是BC的中点,求OD的长.
21.如图,菱形OABC放置在第一象限内,顶点A在x轴上,若顶点B的坐标是(4,3).
(1)请求出菱形边长OA的长度.
(2)反比例函数y经过点C,请求出k的值.
22.如图,在△ABC中,AC=BC,AB⊥x轴于A,反比例函数y(x>0)的图象经过点C,交AB于点D,已知AB=4,BC.
(1)若OA=4,求k的值.
(2)连接OC,若AD=AC,求CO的长.
23.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y(x>0)的图象上,点D的坐标为(3,4).
(1)菱形ABCD的边长为 ;
(2)求k的值;
(3)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
24.如图, OABC的边OA在x轴的正半轴上,OA=5,反比例函数(x>0)的图象经过点C(1,4).
(1)求反比例函数的关系式和点B的坐标;
(2)过AB的中点D作DP∥x轴交反比例函数图象于点P,连接CP,OP.求△COP的面积.
答案
一、选择题.
B.B.C.C.B.D.B.C.B.B.
二、填空题
11.y.
12..
13.2.
14.(3,﹣4).
15.6.
16.4.
17..
18.4.
三.解答题
19.(1)过A作AE⊥BC于E交x轴于F,
则AF∥y轴,
∵BC∥x轴,
∴四边形BOFE是矩形,
∴EF=OB=3,
∵AB=AC,BC=4,
∴BEBC=2,
∴AE,
∴A(2,),
∵反比例函数y(x>0)的图象经过点A,
∴k=29;
(2)设OB=a,
∵BD=AB,
∴A(2,a),D(,a),
∵反比例函数y(x>0)的图象经过点A,交BC于点D,
∴2(a)a,
解得:a=6,
∴OB=6,
∴OC2,
∴四边形ABOC的周长=AB+OB+OC+AC=11+2.
20.(1)∵正方形ABCD的边长为2,点E的坐标为(3,n),
∴OB=3,AB=AD=2,
∴D(1,2),
∵反比例函数y在第一象限的图象经过点D,
∴k=1×2=2,
∴反比例为:y,
∵反比例函数y在第一象限的图象交BC于E,
∴n;
(2)设D(x,2)则E(x+2,1),
∵反比例函数y在第一象限的图象经过点D、点E,
∴2x=x+2,
解得x=2,
∴D(2,2),
∴OA=AD=2,
∴OD2.
21.(1)如图,过B作BD⊥x轴于D,则BD=3,OD=4,
设AO=x=AB,则AD=4﹣x,
∵Rt△ABD中,AD2+BD2=AB2,
∴(4﹣x)2+32=x2,
解得x,
∴菱形边长OA的长度为.
(2)如图,过C作CE⊥x轴于E,则四边形BCED是矩形,
∴BC=DE,CE=BD=3,
∴OE=OD﹣DE=4,
∴点C的坐标为(,3),
∵反比例函数y经过点C,
∴k.
22.(1)作CE⊥AB,垂足为E,
∵AC=BC,AB=4,
∴AE=BE=2.
在Rt△BCE中,BC,BE=2,
∴CE,
∵OA=4,
∴C点的坐标为:(,2),
∵点C在y(x>0)的图象上,
∴k=11;
(2)设A点的坐标为(m,0),
∵AC=BC,AD=AC,
∴AD,
∴D,C两点的坐标分别为:(m,),(m,2).
∵点C,D都在y(x>0)的图象上,
∴m=2(m),
∴m=6,
∴C点的坐标为:(,2),
作CF⊥x轴,垂足为F,
∴OF,CF=2,
在Rt△OFC中,
OC2=OF2+CF2,
∴OC.
23.(1)∵点D的坐标为(3,4),
∴由勾股定理得:OD5,
即菱形ABCD的边长为5,
故答案为:5;
(2)∵菱形ABCD的边长为5,
∴OD=AD=5,AD∥OB,
∵D(3,4),
∴A的坐标为(3,9),
代入y得:k=27,
故答案为:27;
(3)将菱形ABCD沿x轴正方向平移,使得点D落在函数y(x>0)的图象D′点处,
过点D′做x轴的垂线,垂足为F′.
∵DF=4,
∴D′F′=4,
∴点D′的纵坐标为4,
∵点D′在y的图象上,
∴4,
解得:x,
即OF′,
∴FF′3,
∴菱形ABCD平移的距离为.
24.(1)∵反比例函数y(x>0)的图象经过点C(1,4).
∴m=1×4=4,
∴反比例函数的关系式为y(x>0).
∵四边形OABC为平行四边形,且点O(0,0),OA=5,点C(1,4),
∴点A(5,0),
∴点B(6,4).
(2)延长DP交OC于点E,如图所示.
∵点D为线段BA的中点,点A(5,0)、B(6,4),
∴点D(,2).
令y中y=2,则x=2,
∴点P(2,2),
∴PD2,EP=ED﹣PD,
∴S△COPEP (yC﹣yO)(4﹣0)=3.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
