苏科版八年级数学下册 9.4.5正方形 试题(含答案)
文档属性
| 名称 | 苏科版八年级数学下册 9.4.5正方形 试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 141.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 00:00:00 | ||
图片预览


文档简介
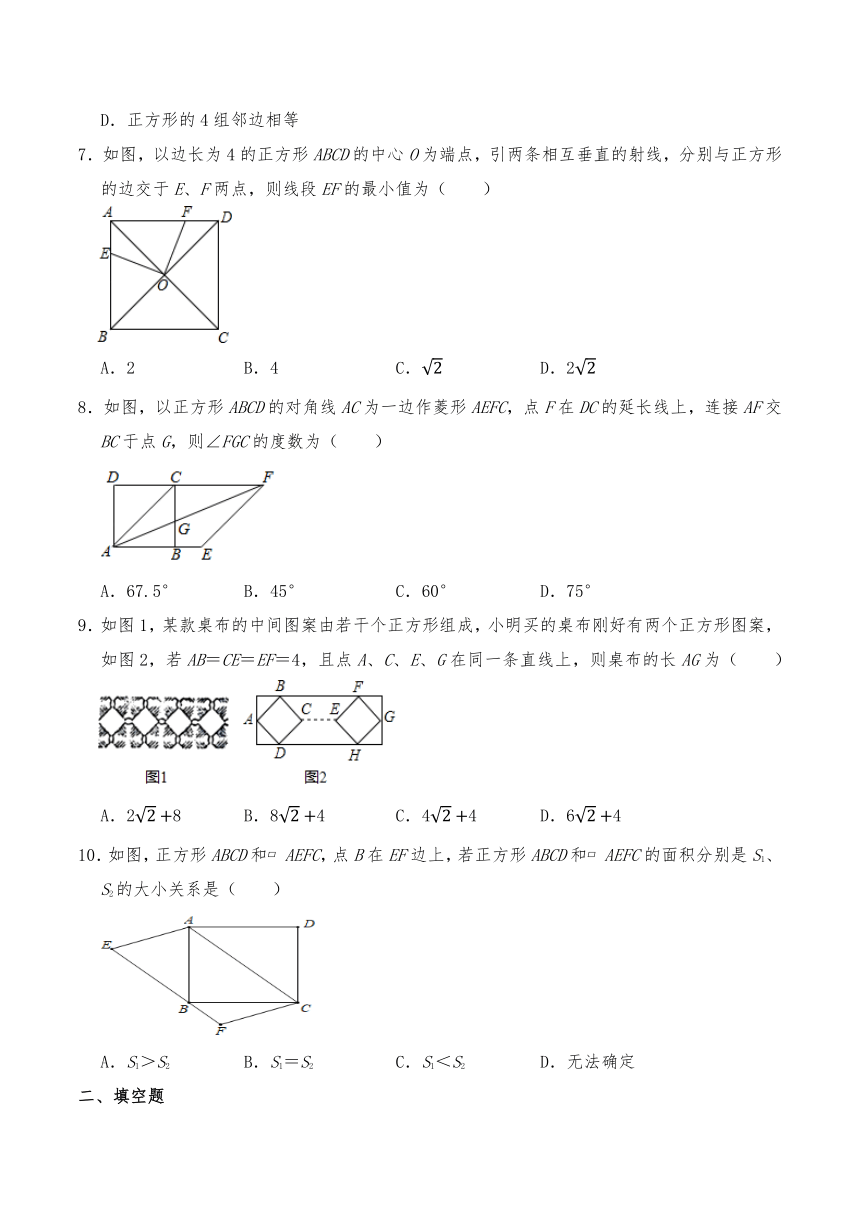
9.4.5正方形
一、选择题.
1.下列图形中仅有两条对称轴的是( )
A.等边三角形 B.长方形 C.圆 D.正方形
2.将三个大小不同的正方形如图放置,顶点处两两相接,若正方形A的边长为4,正方形C的边长为3,则正方形B的面积为( )
A.25 B.5 C.16 D.12
3.在如图所示的若干个正方形拼成的图形中,与三角形ABC全等的三角形是( )
A.△AEG B.△ADF C.△DFG D.△CEG
4.如图,正方形的边长为4,则图中阴影部分的面积为( )
A.2 B.4 C.8 D.无法确定
5.对角线互相垂直且相等四边形一定是( )
A.矩形 B.菱形 C.正方形 D.无法确定
6.下列说法中,正确的是( )
A.平行四边形是特殊的矩形
B.矩形的对角线互相垂直
C.菱形的四只角相等
D.正方形的4组邻边相等
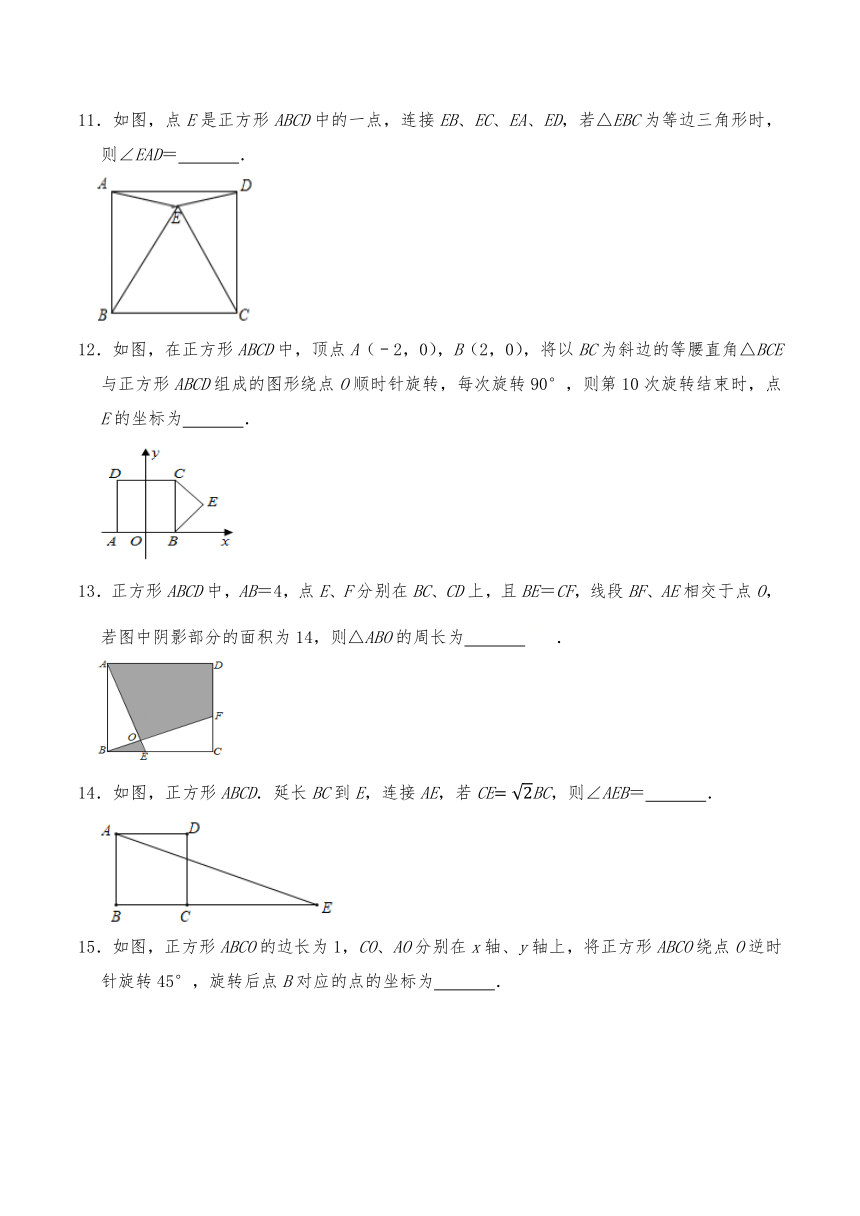
7.如图,以边长为4的正方形ABCD的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于E、F两点,则线段EF的最小值为( )
A.2 B.4 C. D.2
8.如图,以正方形ABCD的对角线AC为一边作菱形AEFC,点F在DC的延长线上,连接AF交BC于点G,则∠FGC的度数为( )
A.67.5° B.45° C.60° D.75°
9.如图1,某款桌布的中间图案由若干个正方形组成,小明买的桌布刚好有两个正方形图案,如图2,若AB=CE=EF=4,且点A、C、E、G在同一条直线上,则桌布的长AG为( )
A.28 B.84 C.44 D.64
10.如图,正方形ABCD和 AEFC,点B在EF边上,若正方形ABCD和 AEFC的面积分别是S1、S2的大小关系是( )
A.S1>S2 B.S1=S2 C.S1<S2 D.无法确定
二、填空题
11.如图,点E是正方形ABCD中的一点,连接EB、EC、EA、ED,若△EBC为等边三角形时,则∠EAD= .
12.如图,在正方形ABCD中,顶点A(﹣2,0),B(2,0),将以BC为斜边的等腰直角△BCE与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第10次旋转结束时,点E的坐标为 .
13.正方形ABCD中,AB=4,点E、F分别在BC、CD上,且BE=CF,线段BF、AE相交于点O,若图中阴影部分的面积为14,则△ABO的周长为 .
14.如图,正方形ABCD.延长BC到E,连接AE,若CEBC,则∠AEB= .
15.如图,正方形ABCO的边长为1,CO、AO分别在x轴、y轴上,将正方形ABCO绕点O逆时针旋转45°,旋转后点B对应的点的坐标为 .
16.如图,正方形ABCD中,点E、F分别是BC、AB边上的点,且AE⊥DF,垂足为点O,△AOD的面积为,则图中阴影部分的面积为 .
17.如图,在正方形ABCD的各边上顺次截取AE=BF=CG=DH=3,若四边形EFGH面积是10,则正方形ABCD的面积为 .
18.如图,正方形ABCD中,E是BD上一点,BE=BA,则∠ACE= .
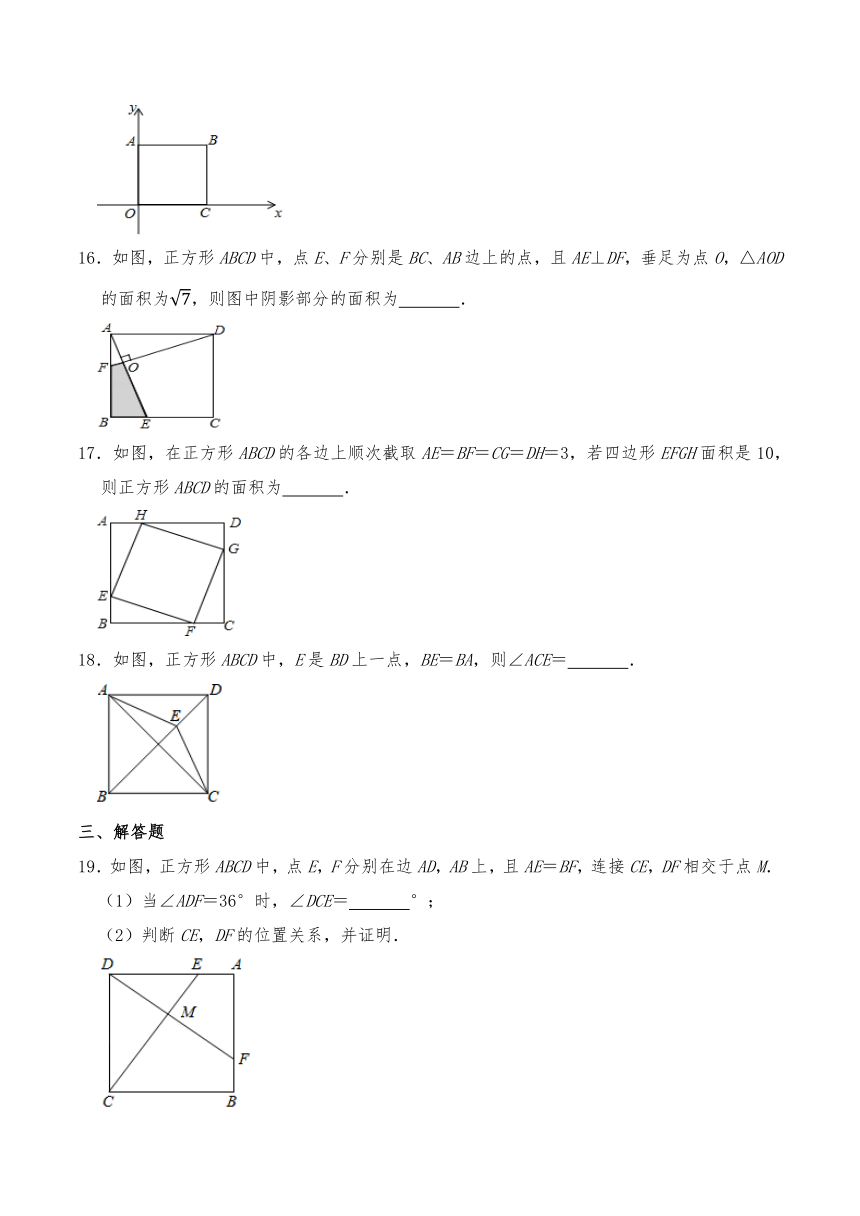
三、解答题
19.如图,正方形ABCD中,点E,F分别在边AD,AB上,且AE=BF,连接CE,DF相交于点M.
(1)当∠ADF=36°时,∠DCE= °;
(2)判断CE,DF的位置关系,并证明.
20.如图,正方形ABCD的对角线AC、BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)判断四边形AECF的形状,并证明你的猜想;
(2)若AB=3,BE=3,求四边形AECF的周长.
21.如图,△EBF为等腰直角三角形,点B为直角顶点,四边形ABCD是正方形.
(1)求证:△ABE≌△CBF;
(2)CF与AE有什么特殊的位置关系?请证明你的结论.
22.如图,AC是正方形ABCD的对角线,E、F分别为BC、CD边上的点,CE=CF,连接AE、AF.
(1)求证:AE=AF;
(2)连接EF,试证明:EF⊥AC.
23.如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上,AB=13,OB=5,E为AC上一点,且∠EBC=∠CBN,直线DE与ON交于点F.
(1)求证:BE=DE;
(2)判断DF与ON的位置关系,并说明理由;
(3)△BEF的周长为 .
24.如图,正方形ABCD中,E是CD边的中点,F是BC边上一点,∠FAE=∠DAE.
(1)求证:AF=AD+CF;
(2)已知正方形ABCD的边长为4.
①求AF之长;
②若P是AE上一点,且△DEP是等腰三角形,则线段EP的长为 .
答案
一、选择题.
B.A.C.C.D.D.D.A.B.B.
二、填空题
11.15°.
12.(﹣4,﹣2).
13.24.
14.22.5°.
15.(0,).
16..
17.16.
18.22.5°.
三、解答题
19.(1)∵四边形ABCD是正方形,
∴CD=AD=AB,∠CDE=∠DAF=90°,
又∵AE=BF,
∴DE=AF,
在△CDE和△DAF中,
,
∴△CDE≌△DAF(SAS),
∴∠DCE=∠ADF,
∵∠ADF=36°,
∴∠DCE=36°,
故答案为:36;
(2)CE,DF的位置关系互相垂直,
证明:由(1)知∠DCE=∠ADF,
∵∠ADF+∠MDC=∠CDE=90°,
∴∠DCE+∠MDC=90°,
∴∠DMC=90°,
∴CE⊥DF,
即CE,DF的位置关系互相垂直.
20.(1)证明:∵正方形ABCD的对角线AC,BD相交于点O,
∴OA=OC,OB=OD,
AC⊥BD.
∵BE=DF,
∴OB+BE=OD+DF,即OE=OF.
∴四边形AECF是平行四边形.
∵AC⊥EF,
∴四边形AECF是菱形.
(2)∵四边形ABCD是正方形,
∴AOAC,BOBD,AC=BD,AC⊥BD,
∴AO=BO,∠AOB=90°.
在直角△AOB中,由勾股定理知:AB3,
∴AO=BO=3.
∴EO=OB+BE=6.
在△AOE中,∠AOE=90°,AE3.
∵四边形AECF是菱形,
∴AE=EC=CF=AF.
∴四边形AECF的周长=4AE=12.
∴四边形AECF的周长是12.
21.证明:(1)∵等腰直角△EBF,
∴BE=BF,∠EBF=90°,
∵正方形ABCD,
∴BA=BC,∠ABC=90°,
∴∠ABE+∠ABF=∠CBF+∠ABF,
∴∠ABE=∠CBF,
在△ABE和△CBF中
∴△ABE≌△CBF(SAS);
(2)CF⊥AE,
理由:延长CF交AB于H,交AE于G,
∵△ABE≌△CBF,
∴∠BAE=∠BCF,
∵∠BCF+∠BHC=90°,
∴∠BAE+∠AHG=90°,
∴∠AGH=90°,
∴CF⊥AE.
22.证明:(1)在正方形ABCD中,则∠ACE=∠ACF=45°,
在△AEC和△AFC中
,
∴△AEC≌△AFC(SAS),
∴AE=AF;
(2)∵CE=CF,∠ACE=∠ACF,
∴EF⊥AC.
23.(1)∵四边形ABCD正方形,
∴CA平分∠BCD,BC=DC,
∴∠BCE=∠DCE=45°,
∵CE=CE,
∴△BCE≌△DCE(SAS),
∴BE=DE.
(2)DF⊥ON,理由如下:
∵△BCE≌△DCE,
∴∠EBC=∠EDC,
∵∠EBC=∠CBN,
∴∠EDC=∠CBN,
∵∠EDC+∠1=90°,∠1=∠2,
∴∠2+∠CBN=90°,
∴∠EFB=90°,
即DF⊥ON;
(3)如图所示,过C作CG⊥ON于G,过D作DH⊥CG于H,则∠CGB=∠AOB=90°,四边形DFGH是矩形,
又∵∠ABC=90°,
∴∠ABO+∠BAO=90°=∠ABO+∠CBG,
∴∠BAO=∠CBG,
又∵AB=BC,
∴△ABO≌△BCG(AAS),
∴BG=AO12,CG=BO=5,
同理可得△CDH≌△BCG,
∴DH=CG=5,CH=BG=12,
∴HG=5+12=17,
∴DF=HG=12,GF=DH=5,
∴BF=BG﹣GF=12﹣5=7,
∴△BEF的周长=BF+EF+BE=BF+EF+DE=BF+DF=7+17=24,
故答案为:24.
24.(1)证明:如图1,过E点作EG⊥AF,垂足为G,连接EF,
(也可延长AE、BC交于P,用全等和等腰三角形知识解决),
∵EG⊥AF,
∴∠EGF=∠AGE=90°,
∵四边形ABCD是正方形,
∴∠C=∠D=90°,
在△AGE和△ADE中,
∴△AGE≌△ADE(AAS),
∴AD=AG,GE=DE,
∵E是CD边的中点,
∴CE=DE,
∴GE=CE,
在Rt△EGF和Rt△ECF中,
∴Rt△EGF≌Rt△ECF(HL),
∴GF=CF,
∵AF=AG+GF,
∴AF=AD+CF;
(2)解:①设CF=x,则BF=4﹣x,AF=4+x,
在Rt△ABF中,AB2+BF2=AF2,
∴42+(4﹣x)2=(4+x)2,
解得:x=1,
∴AF=4+x=4+1=5;
②分三种情况:
i)如图2,PD=DE,过D作DG⊥AE于G,
∴EP=2EG,
Rt△ADE中,AD=4,DE=2,
∴AE2,
∴S△ADE,
即,
∴DG,
由勾股定理得:EG,
∴EP=2EG;
ii)如图3,EP=DE=2;
iii)如图4,PD=PE,过P作PM⊥DE于M,则DM=EM,
∵AD⊥CD,PM⊥DE,
∴AD∥PM,
∴AP=PE,
∵AE=2,
∴EP,
综上,EP的长是2或或.
一、选择题.
1.下列图形中仅有两条对称轴的是( )
A.等边三角形 B.长方形 C.圆 D.正方形
2.将三个大小不同的正方形如图放置,顶点处两两相接,若正方形A的边长为4,正方形C的边长为3,则正方形B的面积为( )
A.25 B.5 C.16 D.12
3.在如图所示的若干个正方形拼成的图形中,与三角形ABC全等的三角形是( )
A.△AEG B.△ADF C.△DFG D.△CEG
4.如图,正方形的边长为4,则图中阴影部分的面积为( )
A.2 B.4 C.8 D.无法确定
5.对角线互相垂直且相等四边形一定是( )
A.矩形 B.菱形 C.正方形 D.无法确定
6.下列说法中,正确的是( )
A.平行四边形是特殊的矩形
B.矩形的对角线互相垂直
C.菱形的四只角相等
D.正方形的4组邻边相等
7.如图,以边长为4的正方形ABCD的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于E、F两点,则线段EF的最小值为( )
A.2 B.4 C. D.2
8.如图,以正方形ABCD的对角线AC为一边作菱形AEFC,点F在DC的延长线上,连接AF交BC于点G,则∠FGC的度数为( )
A.67.5° B.45° C.60° D.75°
9.如图1,某款桌布的中间图案由若干个正方形组成,小明买的桌布刚好有两个正方形图案,如图2,若AB=CE=EF=4,且点A、C、E、G在同一条直线上,则桌布的长AG为( )
A.28 B.84 C.44 D.64
10.如图,正方形ABCD和 AEFC,点B在EF边上,若正方形ABCD和 AEFC的面积分别是S1、S2的大小关系是( )
A.S1>S2 B.S1=S2 C.S1<S2 D.无法确定
二、填空题
11.如图,点E是正方形ABCD中的一点,连接EB、EC、EA、ED,若△EBC为等边三角形时,则∠EAD= .
12.如图,在正方形ABCD中,顶点A(﹣2,0),B(2,0),将以BC为斜边的等腰直角△BCE与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第10次旋转结束时,点E的坐标为 .
13.正方形ABCD中,AB=4,点E、F分别在BC、CD上,且BE=CF,线段BF、AE相交于点O,若图中阴影部分的面积为14,则△ABO的周长为 .
14.如图,正方形ABCD.延长BC到E,连接AE,若CEBC,则∠AEB= .
15.如图,正方形ABCO的边长为1,CO、AO分别在x轴、y轴上,将正方形ABCO绕点O逆时针旋转45°,旋转后点B对应的点的坐标为 .
16.如图,正方形ABCD中,点E、F分别是BC、AB边上的点,且AE⊥DF,垂足为点O,△AOD的面积为,则图中阴影部分的面积为 .
17.如图,在正方形ABCD的各边上顺次截取AE=BF=CG=DH=3,若四边形EFGH面积是10,则正方形ABCD的面积为 .
18.如图,正方形ABCD中,E是BD上一点,BE=BA,则∠ACE= .
三、解答题
19.如图,正方形ABCD中,点E,F分别在边AD,AB上,且AE=BF,连接CE,DF相交于点M.
(1)当∠ADF=36°时,∠DCE= °;
(2)判断CE,DF的位置关系,并证明.
20.如图,正方形ABCD的对角线AC、BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)判断四边形AECF的形状,并证明你的猜想;
(2)若AB=3,BE=3,求四边形AECF的周长.
21.如图,△EBF为等腰直角三角形,点B为直角顶点,四边形ABCD是正方形.
(1)求证:△ABE≌△CBF;
(2)CF与AE有什么特殊的位置关系?请证明你的结论.
22.如图,AC是正方形ABCD的对角线,E、F分别为BC、CD边上的点,CE=CF,连接AE、AF.
(1)求证:AE=AF;
(2)连接EF,试证明:EF⊥AC.
23.如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上,AB=13,OB=5,E为AC上一点,且∠EBC=∠CBN,直线DE与ON交于点F.
(1)求证:BE=DE;
(2)判断DF与ON的位置关系,并说明理由;
(3)△BEF的周长为 .
24.如图,正方形ABCD中,E是CD边的中点,F是BC边上一点,∠FAE=∠DAE.
(1)求证:AF=AD+CF;
(2)已知正方形ABCD的边长为4.
①求AF之长;
②若P是AE上一点,且△DEP是等腰三角形,则线段EP的长为 .
答案
一、选择题.
B.A.C.C.D.D.D.A.B.B.
二、填空题
11.15°.
12.(﹣4,﹣2).
13.24.
14.22.5°.
15.(0,).
16..
17.16.
18.22.5°.
三、解答题
19.(1)∵四边形ABCD是正方形,
∴CD=AD=AB,∠CDE=∠DAF=90°,
又∵AE=BF,
∴DE=AF,
在△CDE和△DAF中,
,
∴△CDE≌△DAF(SAS),
∴∠DCE=∠ADF,
∵∠ADF=36°,
∴∠DCE=36°,
故答案为:36;
(2)CE,DF的位置关系互相垂直,
证明:由(1)知∠DCE=∠ADF,
∵∠ADF+∠MDC=∠CDE=90°,
∴∠DCE+∠MDC=90°,
∴∠DMC=90°,
∴CE⊥DF,
即CE,DF的位置关系互相垂直.
20.(1)证明:∵正方形ABCD的对角线AC,BD相交于点O,
∴OA=OC,OB=OD,
AC⊥BD.
∵BE=DF,
∴OB+BE=OD+DF,即OE=OF.
∴四边形AECF是平行四边形.
∵AC⊥EF,
∴四边形AECF是菱形.
(2)∵四边形ABCD是正方形,
∴AOAC,BOBD,AC=BD,AC⊥BD,
∴AO=BO,∠AOB=90°.
在直角△AOB中,由勾股定理知:AB3,
∴AO=BO=3.
∴EO=OB+BE=6.
在△AOE中,∠AOE=90°,AE3.
∵四边形AECF是菱形,
∴AE=EC=CF=AF.
∴四边形AECF的周长=4AE=12.
∴四边形AECF的周长是12.
21.证明:(1)∵等腰直角△EBF,
∴BE=BF,∠EBF=90°,
∵正方形ABCD,
∴BA=BC,∠ABC=90°,
∴∠ABE+∠ABF=∠CBF+∠ABF,
∴∠ABE=∠CBF,
在△ABE和△CBF中
∴△ABE≌△CBF(SAS);
(2)CF⊥AE,
理由:延长CF交AB于H,交AE于G,
∵△ABE≌△CBF,
∴∠BAE=∠BCF,
∵∠BCF+∠BHC=90°,
∴∠BAE+∠AHG=90°,
∴∠AGH=90°,
∴CF⊥AE.
22.证明:(1)在正方形ABCD中,则∠ACE=∠ACF=45°,
在△AEC和△AFC中
,
∴△AEC≌△AFC(SAS),
∴AE=AF;
(2)∵CE=CF,∠ACE=∠ACF,
∴EF⊥AC.
23.(1)∵四边形ABCD正方形,
∴CA平分∠BCD,BC=DC,
∴∠BCE=∠DCE=45°,
∵CE=CE,
∴△BCE≌△DCE(SAS),
∴BE=DE.
(2)DF⊥ON,理由如下:
∵△BCE≌△DCE,
∴∠EBC=∠EDC,
∵∠EBC=∠CBN,
∴∠EDC=∠CBN,
∵∠EDC+∠1=90°,∠1=∠2,
∴∠2+∠CBN=90°,
∴∠EFB=90°,
即DF⊥ON;
(3)如图所示,过C作CG⊥ON于G,过D作DH⊥CG于H,则∠CGB=∠AOB=90°,四边形DFGH是矩形,
又∵∠ABC=90°,
∴∠ABO+∠BAO=90°=∠ABO+∠CBG,
∴∠BAO=∠CBG,
又∵AB=BC,
∴△ABO≌△BCG(AAS),
∴BG=AO12,CG=BO=5,
同理可得△CDH≌△BCG,
∴DH=CG=5,CH=BG=12,
∴HG=5+12=17,
∴DF=HG=12,GF=DH=5,
∴BF=BG﹣GF=12﹣5=7,
∴△BEF的周长=BF+EF+BE=BF+EF+DE=BF+DF=7+17=24,
故答案为:24.
24.(1)证明:如图1,过E点作EG⊥AF,垂足为G,连接EF,
(也可延长AE、BC交于P,用全等和等腰三角形知识解决),
∵EG⊥AF,
∴∠EGF=∠AGE=90°,
∵四边形ABCD是正方形,
∴∠C=∠D=90°,
在△AGE和△ADE中,
∴△AGE≌△ADE(AAS),
∴AD=AG,GE=DE,
∵E是CD边的中点,
∴CE=DE,
∴GE=CE,
在Rt△EGF和Rt△ECF中,
∴Rt△EGF≌Rt△ECF(HL),
∴GF=CF,
∵AF=AG+GF,
∴AF=AD+CF;
(2)解:①设CF=x,则BF=4﹣x,AF=4+x,
在Rt△ABF中,AB2+BF2=AF2,
∴42+(4﹣x)2=(4+x)2,
解得:x=1,
∴AF=4+x=4+1=5;
②分三种情况:
i)如图2,PD=DE,过D作DG⊥AE于G,
∴EP=2EG,
Rt△ADE中,AD=4,DE=2,
∴AE2,
∴S△ADE,
即,
∴DG,
由勾股定理得:EG,
∴EP=2EG;
ii)如图3,EP=DE=2;
iii)如图4,PD=PE,过P作PM⊥DE于M,则DM=EM,
∵AD⊥CD,PM⊥DE,
∴AD∥PM,
∴AP=PE,
∵AE=2,
∴EP,
综上,EP的长是2或或.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
