九年级数学下册试题 8.2货比三家同步练习-苏科版(含答案)
文档属性
| 名称 | 九年级数学下册试题 8.2货比三家同步练习-苏科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 338.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 13:59:55 | ||
图片预览




文档简介
8.2货比三家
一.选择题
1. “新冠病毒”的英语“NewCoronavirus”中,字母“o”出现的频率是( )
A. B. C.2 D.1
2. 统计得到的一组数据最大值为139,最小值为48,取组距为10,可分成( )
A.10组 B.9组 C.8组 D.7组
3. 为了了解七年级女生的跳绳情况,从中随机抽取了50女生进行1min跳绳测验,得到了这50名女生的跳绳成绩(单位:次),其中最小值为60,最大值为140,若取组距为15,则可分为( )
A.7组 B.6组 C.5组 D.4组
4. 有60个数据,其中最大值为40,最小值为20,若取组距为5,则这组数据分组应该分( )
A.3组 B.4组 C.5组 D.6组
5. 足球运动是全球体育界最具响力的单项体育场动,故有世界第一大运动的美称,为了解某学校校园足球与学生数占学校总人数的百分比,最合适的统计方式是( )
A.折线统计图 B.条形统计图 C.扇形统计图 D.直方图
6. 为了了解某校七年级800名学生的跳绳情况(60秒跳绳的次数),随机对该年级50名学生进行了调查,根据收集的数据绘制了如图所示的频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的次数x为:60≤x<80),则以下说法正确的是( )
A.跳绳次数不少于100次的占80%
B.大多数学生跳绳次数在140﹣160范围内
C.跳绳次数最多的是160次
D.由样本可以估计全年级800人中跳绳次数在60﹣80次的大约有84人
7. 如图为某一试验结果的频率随机试验次数变化趋势图,则下列试验中不符合该图的是( )
A.掷一枚普通正六面体骰子,出现点数不超过2
B.掷一枚硬币,出现正面朝上
C.从装有2个黑球、1个白球的不透明布袋中随机摸出一球为白球
D.从分别标有数字1,2,3,4,5,6,7,8,9的九张卡片中,随机抽取一张卡片所标记的数字不小于7
8. 对一批衬衣进行抽检,统计合格衬衣的件数,得到合格衬衣的频数表如下:
抽取件数 50 100 150 200 500 800 1000
合格频数 42 88 141 176 448 720 900
估计出售2000件衬衣,其中次品大约是( )
A.50件 B.100件 C.150件 D.200件
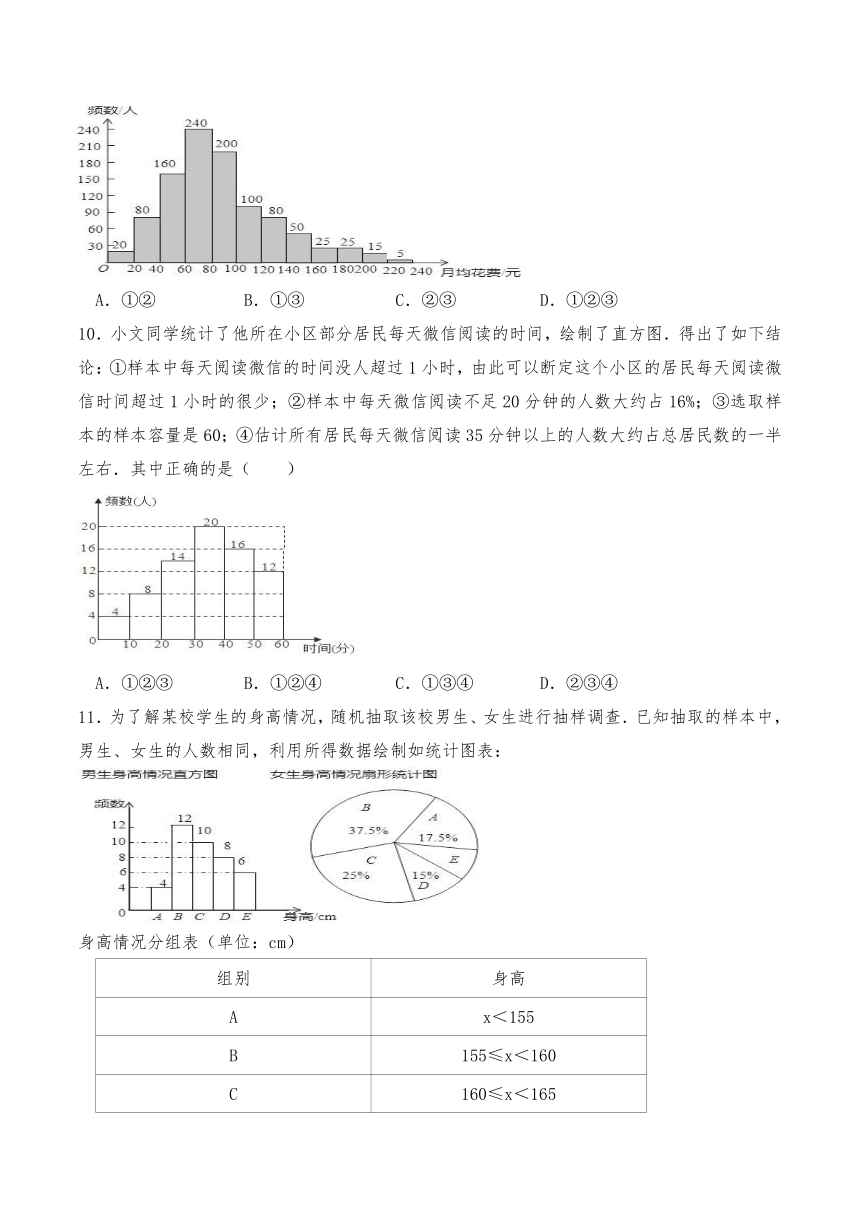
9. 为了了解2018年北京市乘坐地铁的每个人的月均花费情况,相关部门随机调查了1000人乘坐地铁的月均花费(单位:元),绘制了如下频数分布直方图,根据图中信息,下面3个推断中,合理的是( )
①小明乘坐地铁的月均花费是75元,那么在所调查的1000人中至少有一半以上的人月均花费超过小明;
②估计平均每人乘坐地铁的月均花费的范围是60﹣120元;
③如果规定消费达到一定数额可以享受折扣优惠,并且享受折扣优惠的人数控制在20%左右,那么乘坐地铁的月均花费达到120元的人可享受折扣.
A.①② B.①③ C.②③ D.①②③
10.小文同学统计了他所在小区部分居民每天微信阅读的时间,绘制了直方图.得出了如下结论:①样本中每天阅读微信的时间没人超过1小时,由此可以断定这个小区的居民每天阅读微信时间超过1小时的很少;②样本中每天微信阅读不足20分钟的人数大约占16%;③选取样本的样本容量是60;④估计所有居民每天微信阅读35分钟以上的人数大约占总居民数的一半左右.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
11.为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如统计图表:
身高情况分组表(单位:cm)
组别 身高
A x<155
B 155≤x<160
C 160≤x<165
D 165≤x<170
E x≥170
根据图表提供的信息,样本中,身高在160≤x<170之间的女学生人数为( )
A.8 B.6 C.14 D.16
12.某中学举行了“安全知识竞赛“,张岚将所有参赛选手的成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图,部分信息如下:
则下列结论不正确的是( )
A.本次比赛参赛选手共有50人
B.扇形统计图中“89.5~99.5“这一组人数占总参赛人数的百分比为24%
C.频数分布直方图中“84.5~89.5“这一组人数为8人
D.扇形统计图中“89.5~99.5“扇形的圆心角为90°
二.填空题
13.秋季新学期开学,某中学对初一新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格.现随机抽取了部分学生的成绩制作成如下表格,则b= ,c= .
分数段 频数 频率
60≤x<70 6 a
70≤x<80 20 0.4
80≤x<90 15 b
90≤x<100 c 0.18
14.如图是某景点6月份内1~10日每天的最高温度折线统计图,由图信息可知该景点这10天中,气温26℃出现的频率是 .
15.小明将本班全体同学某次数学测试成绩制成了频数分布直方图,图中从左到右各小长方形的高之比为4:3:7:6,且第一小组的频数是12,则小明班的学生人数是 .
16.某中学七年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如下:(如图,每组分数含最小值,不含最大值)根据图、表提供的信息,则80~90分这一组人数最多的班是 .
甲班数学成绩频数分布直方图乙班数学成绩各分数段人数统计图
丙班数学成绩频数统计表
分数 50~60 60~70 70~80 80~90 90~100
人数 1 4 15 11 9
17.将50个数据分成5组列出频数分布表,其中第一组的频数为8,第二组与第五组的频数之和为20,第三组的频率为0.2,则第四组的频率为 .
18.瓯海区开展“明眸皓齿”工程,泽雅中学八年级某班级40名同学经过视力检测,将他们的视力分为6组,前四组的人数分别为10、5、7、6,第五组的频率为0.2,则第六组的频率是 .
19.数学小组对收集到的160个数据进行整理,并绘制出扇形图.发现有一组数据所对应扇形的圆心角是72°,则该组的频数为 .
20.教育部门为了了解全市中小学安全教育情况,对某校进行了“防溺水”安全知识的测试.从七年级随机抽取了50名学生的测试成绩(百分制),整理样本数据,得到下表:
成绩 90≤x≤100 80≤x<90 70≤x<80 60≤x<70 x<60
人数 25 15 5 4 1
根据抽样调查结果,估计该校七年级600名学生中,80分(含80分)以上的学生有 人.
21.自疫情爆发以来,北京市各中小学学生在居家学习期间,坚持开展居家体育锻炼.某校八年级为了解学生的居家锻炼情况,通过视频会议软件,随机抽查了八年级的30名学生的一分钟仰卧起坐的次数,将数据分组整理后,绘制了如图所示的频数分布直方图,估计八年级学生仰卧起坐的次数在30~40次的频率是 .
22.某中学七年级甲、乙、丙三个班中,每班的学生人数都为40名.
某次数学考试的成绩统计如下:(如图,每组分数含最小值,不含最大值)根据图、表提供的信息,则80~90分这一组人数最多的班是 班
三.解答题
23.为了展现新时代青年学子勇于担当的责任感和强烈的爱国情怀,自治区教育工委、教育厅组织开展了全区学生“共抗疫情、爱国力行”网络文化作品征集展示活动,现将从中挑选的50件参赛作品的成绩(单位:分)统计如表:
等级 成绩(用m表示) 频数 频率
A 90≤m≤100 x 0.08
B 80≤m<90 34 y
C m<80 12 0.24
合计 50 1
请根据上表提供的信息,解答下列问题:
(1)表中x的值为 ,y的值为 (直接填写结果);
(2)将本次参赛作品获得A等级的学生依次用A1、A2、A3…表示.若从本次参赛作品获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,用列表或画树状图的方法,求恰好抽到学生A1和A2概率.
24.中国国际进口博览会的成功举办成为共建“一带一路”的又一个重要支撑.某兴趣小组对某天申请参展的企业中信用等级在B等级及以上的进行了调查,根据调查结果绘制了如下尚不完整的统计图表.
调查结果统计表
组别 信用等级 频数
第一组 AAA 32
第二组 AA 144
第三组 BBB c
第四组 BB 88
第五组 B e
请结合图表提供的信息回答下列问题:
(1)填空:这天进行申请的企业共有 家,c= , ;
(2)在扇形统计图中,第3组所在扇形的圆心角的度数是 ;
(3)若这天参与申请的企业信用等级在BBB级及以上的数量约占整个申请阶段的6%,请你估计整个申请阶段参与申请的企业数量.
25.某校团委为了解该校七年级学生最喜欢的课余活动情况,采用随机抽样的方法进行了问卷调查,被调查学生必须从“运动、娱乐、阅读、其他”四项中选择其中的一项,以下是根据调查结果绘制的统计图表的一部分,
活动类型 频数(人数) 频率
运动 20
娱乐 40
阅读
其他 0.1
根据以上图表信息,解答下列问题:
(1)在被调查的学生中,最喜欢“运动”的学生人数为 人,最喜欢“娱乐”的学生人数占被调查学生人数的百分比为 %.
(2)本次调查的样本容量是 ,最喜欢“其他”的学生人数为 人.
(3)若该校七年级共有360名学生,试估计最喜欢“阅读”的学生人数.
26.某校组织全校2000名学生进行了时事知识竞赛.为了解成绩的分布情况,随机抽取了部分学生的成绩(得分取整数,满分为100分),并绘制了频数分布表和频数分布直方图(不完整).
分组 50.5≤x<60.5 60.5≤x<70.5 70.5≤x<80.5 80.5≤x<90.5 90.5≤x<100.5 合计
频数 20 48 a 104 148 400
根据所给信息,回答下列问题:
(1)频数分布表中,a= ;
(2)补全频数分布直方图;
(3)学校将对分数x在90.5≤x<100.5范围内的学生进行奖励,请你估算出全校获奖学生的人数.
27.初三年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有12000名初三学生,那么在试卷评讲课中,“独立思考”的初三学生约有多少人?
28.为了了解我市中学生跳绳活动开展的情况,随机抽查了全市八年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制成如下的两个不完整的统计图:
请根据图中提供的信息,解答下列问题:
(1)本次共抽查了多少名学生?请补全频数分布直方图;
(2)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生的成绩为优秀;
(3)请你根据以上信息,对我市开展的学生跳绳活动情况谈谈自己的看法或建议.
29.为节约水资源,某市已于2023年1月按居民家庭年用水量实行阶梯水价,水价分档递增.每户家庭年用水量分档如表:
第一档 第二档 第三档
年用水量(m3) 180及以下 181﹣240 241及以上
为了解阶梯水价实行三年来有关情况,有关部门随机抽查了该市5万户家庭的年用水量(取整数,单位:m3),绘制了如图所示的统计图(每组只含最大值,不含最小值).已知最初的设计目标是使第一档、第二档和第三档水价用户分别占全市家庭的80%、15%和5%,且上下波动不超过0.5%.结合图表回答下列问题.
(1)实施过程中,第一档水价用户标准符合最初的设计目标吗?为什么?
(2)若该市有120万户家庭用户,估计该市居民家庭年用水量在90m3~120m3这一组的户数.
(3)请结合所给数据,发表一条你的观点或提出一条建议.
30.为了调查居民的生活水平,有关部门对某居委会的50户居民的家庭存款额进行了调查,数据(单位:万元)如下:
1.7 3.5 2.3 6.4 2.0 1.9 6.7 4.8 5.0 4.7
2.3 3.4 5.6 3.7 2.2 3.3 5.8 4.3 3.6 3.8
3.0 5.1 7.0 3.1 2.9 4.9 5.8 3.6 3.0 4.2
4.0 3.9 5.1 6.3 1.8 3.2 5.1 5.7 3.9 3.1
2.5 2.8 4.5 4.9 5.3 2.6 7.2 1.9 5.0 3.8
(1)这50个家庭存款额的最大值、最小值分别是多少?它们相差多少?
(2)填表:
存款额x(万元) 划记 户数
1.0≤x<2.0
2.0≤x<3.0
3.0≤x<4.0
4.0≤x<5.0
5.0≤x<6.0
6.0≤x<7.0
7.0≤x<8.0
(3)根据上表谈谈这50户家庭存款额的分布情况.
答案
一.选择题
B.A.B.C.C.A.B.D.D.B.D.D.
二.填空题
13.0.3,9.
14.0.3.
15.60.
16.甲班.
17.0.24.
18.0.1.
19.32.
20.480.
21.0.4.
22.甲.
三.解答题
23.(1)50﹣12﹣34=4,34÷50=0.68,
故答案为4,0.68;
(2)用列表法表示所有可能出现的结果情况如下:
∵共有12种等可能的结果,其中恰好抽到A1和A2的结果有2种,
∴恰好抽到 A1和A2的概率为P.
24.(1)这天进行申请的企业共有:144÷45%=320(家),
m%=32÷320×100%=10%,e=320×5%=16,
c=320﹣32﹣144﹣88﹣16=40,
n%=40÷320×100%=12.5%,
∴m=10,n=12.5,
∴,
故答案为320,40,;
(2)在扇形统计图中,第3组所在扇形的圆心角的度数是360°×12.5%=45°,
故答案为45°;
(3)320﹣16﹣88=216(家),
216÷6%=3600(家),
答:整个申请阶段参与申请的企业数量为3600家.
25.(1)从统计图表中,可得最喜欢“运动”的有20人,最喜欢“娱乐”的学生人数占被调查学生人数的百分比为40%,
故答案为20,40;
(2)40÷40%=100(人),100×0.1=10(人),
故答案为100,10;
(3)360108(人),
答:该校七年级360名学生中最喜欢“阅读”的学生有108人.
26.(1)a=400﹣148﹣104﹣48﹣20=80,
故答案为80;
(2)补全频数分布直方图如下:
(3)2000740(人),
答:全校2000名学生中获奖的大约有740人.
27.(1)在这次评价中,一共抽查了224÷40%=560名学生,
故答案为560;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为360°54°,
故答案为54;
(3)讲解题目的学生有:560﹣(84+168+224)=84(人),
补充完整的频数分布直方图如右图所示;
(4)120003600(人),
在试卷评讲课中,“独立思考”的初三学生约有3600人.
28.(1)24÷12%=200 名,200﹣8﹣16﹣71﹣60﹣16=29名,补全条形统计图如图所示:
(2)80004200名,
答:估计全市8000名八年级学生中有4200名学生的成绩为优秀;
(3)继续加强锻炼,加强跳绳的技巧性训练,增加优秀率.
29.(1)∵80%,
∴实施方案中,第一档水价用户标准符合最初的设计目标;
(2)∵120=36,
∴该市居民家庭年用水量在90m3~120m3这一组的约有36万户;
(3)第二档、第三档水价用户分别占全市家庭用户的13%、7%,实施方案不符合最初的设计目标.
30.(1)存款额的最大值为7.2万元,存款额的最小值为1.7万元,相差:7.2﹣1.7=5.5(万元);
(2)根据划记可得,1.0≤x<2.0一组的户数为4,2.0≤x<3.0一组的户数为8,3.0≤x<4.0一组的户数为15,4.0≤x<5.0一组的户数为8,5.0≤x<6.0一组的户数为10,6.0≤x<7.0一组的户数为3,7.0≤x<8.0一组的户数为2;
故答案为4,8,15,8,10,3,2.
(3)由表可得,这50户家庭中,存款额在2.0≤x<6.0范围内的户数较多,其中在3.0≤x<4.0范围内的户数最多,而存款额在1.0≤x<2.0,6.0≤x<8.0范围内户数较少,占小部分.
一.选择题
1. “新冠病毒”的英语“NewCoronavirus”中,字母“o”出现的频率是( )
A. B. C.2 D.1
2. 统计得到的一组数据最大值为139,最小值为48,取组距为10,可分成( )
A.10组 B.9组 C.8组 D.7组
3. 为了了解七年级女生的跳绳情况,从中随机抽取了50女生进行1min跳绳测验,得到了这50名女生的跳绳成绩(单位:次),其中最小值为60,最大值为140,若取组距为15,则可分为( )
A.7组 B.6组 C.5组 D.4组
4. 有60个数据,其中最大值为40,最小值为20,若取组距为5,则这组数据分组应该分( )
A.3组 B.4组 C.5组 D.6组
5. 足球运动是全球体育界最具响力的单项体育场动,故有世界第一大运动的美称,为了解某学校校园足球与学生数占学校总人数的百分比,最合适的统计方式是( )
A.折线统计图 B.条形统计图 C.扇形统计图 D.直方图
6. 为了了解某校七年级800名学生的跳绳情况(60秒跳绳的次数),随机对该年级50名学生进行了调查,根据收集的数据绘制了如图所示的频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的次数x为:60≤x<80),则以下说法正确的是( )
A.跳绳次数不少于100次的占80%
B.大多数学生跳绳次数在140﹣160范围内
C.跳绳次数最多的是160次
D.由样本可以估计全年级800人中跳绳次数在60﹣80次的大约有84人
7. 如图为某一试验结果的频率随机试验次数变化趋势图,则下列试验中不符合该图的是( )
A.掷一枚普通正六面体骰子,出现点数不超过2
B.掷一枚硬币,出现正面朝上
C.从装有2个黑球、1个白球的不透明布袋中随机摸出一球为白球
D.从分别标有数字1,2,3,4,5,6,7,8,9的九张卡片中,随机抽取一张卡片所标记的数字不小于7
8. 对一批衬衣进行抽检,统计合格衬衣的件数,得到合格衬衣的频数表如下:
抽取件数 50 100 150 200 500 800 1000
合格频数 42 88 141 176 448 720 900
估计出售2000件衬衣,其中次品大约是( )
A.50件 B.100件 C.150件 D.200件
9. 为了了解2018年北京市乘坐地铁的每个人的月均花费情况,相关部门随机调查了1000人乘坐地铁的月均花费(单位:元),绘制了如下频数分布直方图,根据图中信息,下面3个推断中,合理的是( )
①小明乘坐地铁的月均花费是75元,那么在所调查的1000人中至少有一半以上的人月均花费超过小明;
②估计平均每人乘坐地铁的月均花费的范围是60﹣120元;
③如果规定消费达到一定数额可以享受折扣优惠,并且享受折扣优惠的人数控制在20%左右,那么乘坐地铁的月均花费达到120元的人可享受折扣.
A.①② B.①③ C.②③ D.①②③
10.小文同学统计了他所在小区部分居民每天微信阅读的时间,绘制了直方图.得出了如下结论:①样本中每天阅读微信的时间没人超过1小时,由此可以断定这个小区的居民每天阅读微信时间超过1小时的很少;②样本中每天微信阅读不足20分钟的人数大约占16%;③选取样本的样本容量是60;④估计所有居民每天微信阅读35分钟以上的人数大约占总居民数的一半左右.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
11.为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如统计图表:
身高情况分组表(单位:cm)
组别 身高
A x<155
B 155≤x<160
C 160≤x<165
D 165≤x<170
E x≥170
根据图表提供的信息,样本中,身高在160≤x<170之间的女学生人数为( )
A.8 B.6 C.14 D.16
12.某中学举行了“安全知识竞赛“,张岚将所有参赛选手的成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图,部分信息如下:
则下列结论不正确的是( )
A.本次比赛参赛选手共有50人
B.扇形统计图中“89.5~99.5“这一组人数占总参赛人数的百分比为24%
C.频数分布直方图中“84.5~89.5“这一组人数为8人
D.扇形统计图中“89.5~99.5“扇形的圆心角为90°
二.填空题
13.秋季新学期开学,某中学对初一新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格.现随机抽取了部分学生的成绩制作成如下表格,则b= ,c= .
分数段 频数 频率
60≤x<70 6 a
70≤x<80 20 0.4
80≤x<90 15 b
90≤x<100 c 0.18
14.如图是某景点6月份内1~10日每天的最高温度折线统计图,由图信息可知该景点这10天中,气温26℃出现的频率是 .
15.小明将本班全体同学某次数学测试成绩制成了频数分布直方图,图中从左到右各小长方形的高之比为4:3:7:6,且第一小组的频数是12,则小明班的学生人数是 .
16.某中学七年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如下:(如图,每组分数含最小值,不含最大值)根据图、表提供的信息,则80~90分这一组人数最多的班是 .
甲班数学成绩频数分布直方图乙班数学成绩各分数段人数统计图
丙班数学成绩频数统计表
分数 50~60 60~70 70~80 80~90 90~100
人数 1 4 15 11 9
17.将50个数据分成5组列出频数分布表,其中第一组的频数为8,第二组与第五组的频数之和为20,第三组的频率为0.2,则第四组的频率为 .
18.瓯海区开展“明眸皓齿”工程,泽雅中学八年级某班级40名同学经过视力检测,将他们的视力分为6组,前四组的人数分别为10、5、7、6,第五组的频率为0.2,则第六组的频率是 .
19.数学小组对收集到的160个数据进行整理,并绘制出扇形图.发现有一组数据所对应扇形的圆心角是72°,则该组的频数为 .
20.教育部门为了了解全市中小学安全教育情况,对某校进行了“防溺水”安全知识的测试.从七年级随机抽取了50名学生的测试成绩(百分制),整理样本数据,得到下表:
成绩 90≤x≤100 80≤x<90 70≤x<80 60≤x<70 x<60
人数 25 15 5 4 1
根据抽样调查结果,估计该校七年级600名学生中,80分(含80分)以上的学生有 人.
21.自疫情爆发以来,北京市各中小学学生在居家学习期间,坚持开展居家体育锻炼.某校八年级为了解学生的居家锻炼情况,通过视频会议软件,随机抽查了八年级的30名学生的一分钟仰卧起坐的次数,将数据分组整理后,绘制了如图所示的频数分布直方图,估计八年级学生仰卧起坐的次数在30~40次的频率是 .
22.某中学七年级甲、乙、丙三个班中,每班的学生人数都为40名.
某次数学考试的成绩统计如下:(如图,每组分数含最小值,不含最大值)根据图、表提供的信息,则80~90分这一组人数最多的班是 班
三.解答题
23.为了展现新时代青年学子勇于担当的责任感和强烈的爱国情怀,自治区教育工委、教育厅组织开展了全区学生“共抗疫情、爱国力行”网络文化作品征集展示活动,现将从中挑选的50件参赛作品的成绩(单位:分)统计如表:
等级 成绩(用m表示) 频数 频率
A 90≤m≤100 x 0.08
B 80≤m<90 34 y
C m<80 12 0.24
合计 50 1
请根据上表提供的信息,解答下列问题:
(1)表中x的值为 ,y的值为 (直接填写结果);
(2)将本次参赛作品获得A等级的学生依次用A1、A2、A3…表示.若从本次参赛作品获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,用列表或画树状图的方法,求恰好抽到学生A1和A2概率.
24.中国国际进口博览会的成功举办成为共建“一带一路”的又一个重要支撑.某兴趣小组对某天申请参展的企业中信用等级在B等级及以上的进行了调查,根据调查结果绘制了如下尚不完整的统计图表.
调查结果统计表
组别 信用等级 频数
第一组 AAA 32
第二组 AA 144
第三组 BBB c
第四组 BB 88
第五组 B e
请结合图表提供的信息回答下列问题:
(1)填空:这天进行申请的企业共有 家,c= , ;
(2)在扇形统计图中,第3组所在扇形的圆心角的度数是 ;
(3)若这天参与申请的企业信用等级在BBB级及以上的数量约占整个申请阶段的6%,请你估计整个申请阶段参与申请的企业数量.
25.某校团委为了解该校七年级学生最喜欢的课余活动情况,采用随机抽样的方法进行了问卷调查,被调查学生必须从“运动、娱乐、阅读、其他”四项中选择其中的一项,以下是根据调查结果绘制的统计图表的一部分,
活动类型 频数(人数) 频率
运动 20
娱乐 40
阅读
其他 0.1
根据以上图表信息,解答下列问题:
(1)在被调查的学生中,最喜欢“运动”的学生人数为 人,最喜欢“娱乐”的学生人数占被调查学生人数的百分比为 %.
(2)本次调查的样本容量是 ,最喜欢“其他”的学生人数为 人.
(3)若该校七年级共有360名学生,试估计最喜欢“阅读”的学生人数.
26.某校组织全校2000名学生进行了时事知识竞赛.为了解成绩的分布情况,随机抽取了部分学生的成绩(得分取整数,满分为100分),并绘制了频数分布表和频数分布直方图(不完整).
分组 50.5≤x<60.5 60.5≤x<70.5 70.5≤x<80.5 80.5≤x<90.5 90.5≤x<100.5 合计
频数 20 48 a 104 148 400
根据所给信息,回答下列问题:
(1)频数分布表中,a= ;
(2)补全频数分布直方图;
(3)学校将对分数x在90.5≤x<100.5范围内的学生进行奖励,请你估算出全校获奖学生的人数.
27.初三年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有12000名初三学生,那么在试卷评讲课中,“独立思考”的初三学生约有多少人?
28.为了了解我市中学生跳绳活动开展的情况,随机抽查了全市八年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制成如下的两个不完整的统计图:
请根据图中提供的信息,解答下列问题:
(1)本次共抽查了多少名学生?请补全频数分布直方图;
(2)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生的成绩为优秀;
(3)请你根据以上信息,对我市开展的学生跳绳活动情况谈谈自己的看法或建议.
29.为节约水资源,某市已于2023年1月按居民家庭年用水量实行阶梯水价,水价分档递增.每户家庭年用水量分档如表:
第一档 第二档 第三档
年用水量(m3) 180及以下 181﹣240 241及以上
为了解阶梯水价实行三年来有关情况,有关部门随机抽查了该市5万户家庭的年用水量(取整数,单位:m3),绘制了如图所示的统计图(每组只含最大值,不含最小值).已知最初的设计目标是使第一档、第二档和第三档水价用户分别占全市家庭的80%、15%和5%,且上下波动不超过0.5%.结合图表回答下列问题.
(1)实施过程中,第一档水价用户标准符合最初的设计目标吗?为什么?
(2)若该市有120万户家庭用户,估计该市居民家庭年用水量在90m3~120m3这一组的户数.
(3)请结合所给数据,发表一条你的观点或提出一条建议.
30.为了调查居民的生活水平,有关部门对某居委会的50户居民的家庭存款额进行了调查,数据(单位:万元)如下:
1.7 3.5 2.3 6.4 2.0 1.9 6.7 4.8 5.0 4.7
2.3 3.4 5.6 3.7 2.2 3.3 5.8 4.3 3.6 3.8
3.0 5.1 7.0 3.1 2.9 4.9 5.8 3.6 3.0 4.2
4.0 3.9 5.1 6.3 1.8 3.2 5.1 5.7 3.9 3.1
2.5 2.8 4.5 4.9 5.3 2.6 7.2 1.9 5.0 3.8
(1)这50个家庭存款额的最大值、最小值分别是多少?它们相差多少?
(2)填表:
存款额x(万元) 划记 户数
1.0≤x<2.0
2.0≤x<3.0
3.0≤x<4.0
4.0≤x<5.0
5.0≤x<6.0
6.0≤x<7.0
7.0≤x<8.0
(3)根据上表谈谈这50户家庭存款额的分布情况.
答案
一.选择题
B.A.B.C.C.A.B.D.D.B.D.D.
二.填空题
13.0.3,9.
14.0.3.
15.60.
16.甲班.
17.0.24.
18.0.1.
19.32.
20.480.
21.0.4.
22.甲.
三.解答题
23.(1)50﹣12﹣34=4,34÷50=0.68,
故答案为4,0.68;
(2)用列表法表示所有可能出现的结果情况如下:
∵共有12种等可能的结果,其中恰好抽到A1和A2的结果有2种,
∴恰好抽到 A1和A2的概率为P.
24.(1)这天进行申请的企业共有:144÷45%=320(家),
m%=32÷320×100%=10%,e=320×5%=16,
c=320﹣32﹣144﹣88﹣16=40,
n%=40÷320×100%=12.5%,
∴m=10,n=12.5,
∴,
故答案为320,40,;
(2)在扇形统计图中,第3组所在扇形的圆心角的度数是360°×12.5%=45°,
故答案为45°;
(3)320﹣16﹣88=216(家),
216÷6%=3600(家),
答:整个申请阶段参与申请的企业数量为3600家.
25.(1)从统计图表中,可得最喜欢“运动”的有20人,最喜欢“娱乐”的学生人数占被调查学生人数的百分比为40%,
故答案为20,40;
(2)40÷40%=100(人),100×0.1=10(人),
故答案为100,10;
(3)360108(人),
答:该校七年级360名学生中最喜欢“阅读”的学生有108人.
26.(1)a=400﹣148﹣104﹣48﹣20=80,
故答案为80;
(2)补全频数分布直方图如下:
(3)2000740(人),
答:全校2000名学生中获奖的大约有740人.
27.(1)在这次评价中,一共抽查了224÷40%=560名学生,
故答案为560;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为360°54°,
故答案为54;
(3)讲解题目的学生有:560﹣(84+168+224)=84(人),
补充完整的频数分布直方图如右图所示;
(4)120003600(人),
在试卷评讲课中,“独立思考”的初三学生约有3600人.
28.(1)24÷12%=200 名,200﹣8﹣16﹣71﹣60﹣16=29名,补全条形统计图如图所示:
(2)80004200名,
答:估计全市8000名八年级学生中有4200名学生的成绩为优秀;
(3)继续加强锻炼,加强跳绳的技巧性训练,增加优秀率.
29.(1)∵80%,
∴实施方案中,第一档水价用户标准符合最初的设计目标;
(2)∵120=36,
∴该市居民家庭年用水量在90m3~120m3这一组的约有36万户;
(3)第二档、第三档水价用户分别占全市家庭用户的13%、7%,实施方案不符合最初的设计目标.
30.(1)存款额的最大值为7.2万元,存款额的最小值为1.7万元,相差:7.2﹣1.7=5.5(万元);
(2)根据划记可得,1.0≤x<2.0一组的户数为4,2.0≤x<3.0一组的户数为8,3.0≤x<4.0一组的户数为15,4.0≤x<5.0一组的户数为8,5.0≤x<6.0一组的户数为10,6.0≤x<7.0一组的户数为3,7.0≤x<8.0一组的户数为2;
故答案为4,8,15,8,10,3,2.
(3)由表可得,这50户家庭中,存款额在2.0≤x<6.0范围内的户数较多,其中在3.0≤x<4.0范围内的户数最多,而存款额在1.0≤x<2.0,6.0≤x<8.0范围内户数较少,占小部分.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
