2023年新疆维吾尔自治区普通高中学业水平考试数学模拟试卷(四)(含答案)
文档属性
| 名称 | 2023年新疆维吾尔自治区普通高中学业水平考试数学模拟试卷(四)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 279.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-08 22:53:59 | ||
图片预览



文档简介
新疆维吾尔自治区普通高中学业水平考试
数学模拟试卷(四)
第Ⅰ卷 (选择题,共48分)
一、选择题(本大题16小题,每小题3分,共48分。在下列各小题给出的四个选项中,只有一项是符合题目要求的。请将正确答案的序号填入下表。)
(1)已知集合,,则
A. B. C. D.
(2)已知角的终边过点P(-4,3), 则的值是
A. B. C. D.
(3)某几何体的三视图如图1所示,它的体积为
A. B. C. D.
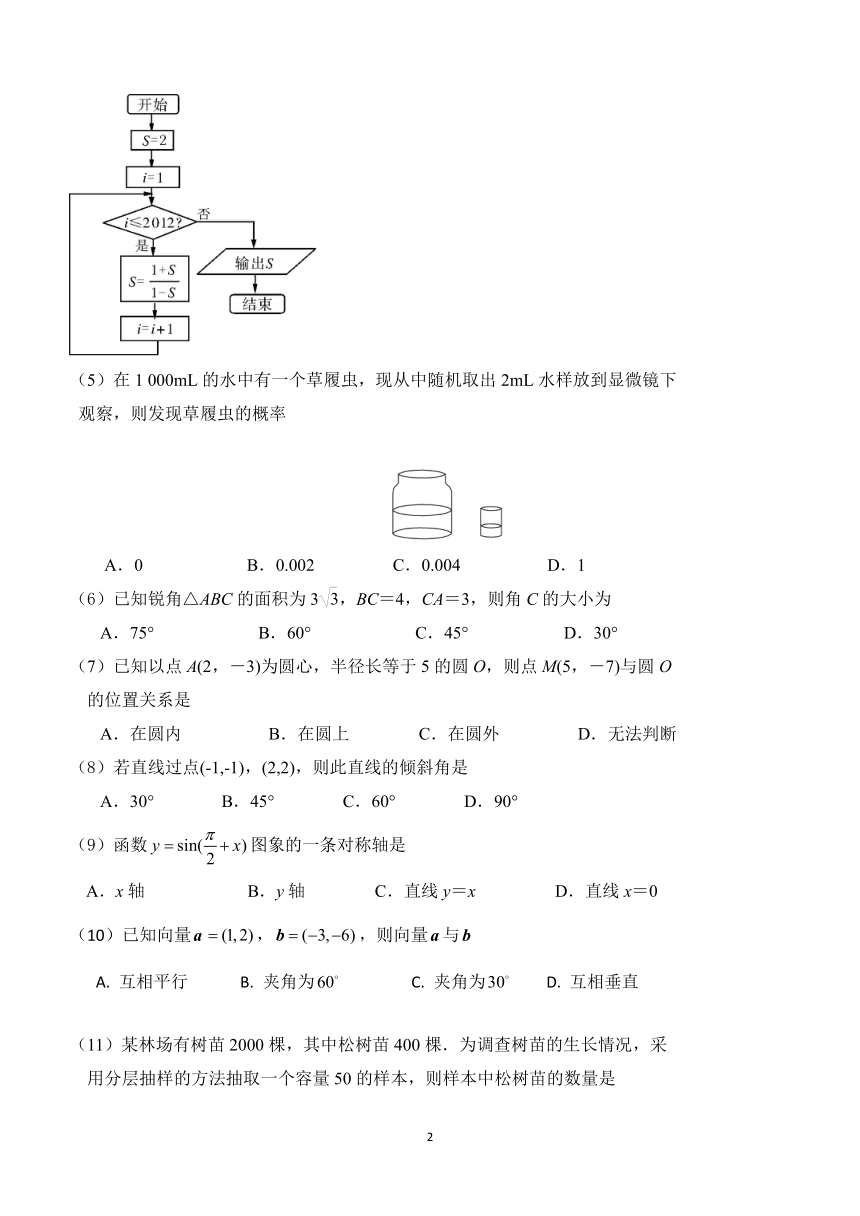
(4) 某程序框图如图,该程序运行后输出的值是
A.-3 B.- C. D.2
在1 000mL的水中有一个草履虫,现从中随机取出2mL水样放到显微镜下
观察,则发现草履虫的概率
A.0 B.0.002 C.0.004 D.1
(6)已知锐角△ABC的面积为3,BC=4,CA=3,则角C的大小为
A.75° B.60° C.45° D.30°
已知以点A(2,-3)为圆心,半径长等于5的圆O,则点M(5,-7)与圆O
的位置关系是
A.在圆内 B.在圆上 C.在圆外 D.无法判断
(8)若直线过点(-1,-1),(2,2),则此直线的倾斜角是
A.30° B.45° C.60° D.90°
(9)函数图象的一条对称轴是
A.x轴 B.y轴 C.直线y=x D.直线x=0
(10)已知向量,,则向量与
A. 互相平行 B. 夹角为 C. 夹角为 D. 互相垂直
某林场有树苗2000棵,其中松树苗400棵.为调查树苗的生长情况,采
用分层抽样的方法抽取一个容量50的样本,则样本中松树苗的数量是
A.40 B.30 C.20 D.10
已知点P(x,y)在不等式组表示的平面区域上运动,
则z=x-y的取值范围是
A.[-2,-1] B.[-2,1 C.[-1,2] D.[1,2]
(13) 已知, 则的值为
A. B. 7 C. D.
(14)等比数列{an}中,a1+a2+a3+…+an=2n-1,则a12+a22+a32+…+an2等于
A B C D
设a、b∈R+,若a+b=1,则+的最小值等于
A.1 B.3 C.2 D.4
设是定义在上的函数,其图像关于原点对称,且当>0时,,则( )
A.1 B.-1 C. D.
第Ⅱ卷 (非选择题,共52分)
二、填空题(本大题共4小题,每小题4分,共16分。请将答案直接填在题中的横线上。)
17. 用二分法求方程x3-2x-5=0在区间[2,3]上的近似解,取区间中点x0=2.5,那么下一个有解区间为________.
有4所自主招生的大学,甲、乙两位同学各自选择其中一所学校参加考试,
若每位同学选择每所大学的可能性相同,则这两位同学选择同一所大学的概率为
________。
19. 两条直线l1:2x+3y-m=0与l2:x-my+12=0的交点在y轴上,那么m
的值为_________。
20. 已知函数f(x)=Asin(ωx+φ)(ω>0)的图象如图所示,则A+ω=________.
三、解答题(本大题共6小题,每小题6分,共36分。解答应写出文字说明,证明过程或者演算步骤。)
21.用单调性定义证明:函数在上是增函数。
22. 某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
(I)求回归直线方程=bx+a,其中b=-20,a=-b;
(II)预计在今后的销售中,销量与单价仍然服从(I)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
23.设Sn为数列{an}的前n项和,Sn=kn2+n,n∈N*,其中k是常数.
(1) 求a1及an;
(2) 若对于任意的m∈N*,am,a2m,a4m成等比数列,求k的值.
24. 已知函数f(x)=sin(x+)+cos(x-),x∈R.
(1)求f(x)的最小正周期和最小值;
(2)已知cos(β-α)=,cos(β+α)=-,0<α<β≤.
求证:[f(β)]2-2=0.
解:(1)∵f(x)=sin(x+-2π)+sin(x-+)
=sin(x-)+sin(x-)
=2sin(x-),
∴f(x)的最小正周期为T=2π,最小值为-2.
(2)证明:由已知得cos βcos α+sin βsin α=,
cos βcos α-sin βsin α=-.
两式相加得2cos βcos α=0.
∵0<α<β≤,∴β=.
∴[f(β)]2-2=4sin2-2=0.
25. 如图所示,P为平行四边形ABCD所在平面外一点,M、N分别为AB、PC的中点,平面PAD∩平面PBC=l.
(1) 求证:BC∥l;
(2) MN与平面PAD是否平行?试证明你的结论.
已知圆C:x2+y2-2x-4y-20=0及直线l:(2m+1)x+(m+1)y=7m+4
(m∈R).
(1) 证明:不论m取什么实数,直线l与圆C总相交;
(2) 求直线l被圆C截得的弦长的最小值及此时的直线方程.
高中学业水平考试数学模拟试卷(四)
参考答案
一、DDCDB BBBDA DCCDDB
二、17. [2,2.5] 18 . 19. m=±6 20.
三、21. 证明:任取则
……3分
又,即,
∴ 函数在上是增函数。……6分
22. 解:(I)
……3分
(II)工厂获得利润
当时,(元)……6分
23.解 (1) 由Sn=kn2+n,得a1=S1=k+1.
当n≥2时,an=Sn-Sn-1=2kn-k+1.
经验证,n=1时,上式也成立,
∴an=2kn-k+1.……3分
(2) ∵am,a2m,a4m成等比数列,∴a=am·a4m,
即(4mk-k+1)2=(2km-k+1)(8km-k+1),
整理得mk(k-1)=0.
∵对任意的m∈N*成立, ∴k=0或k=1.……6分
24. 解 ∵=(1,3),=(2,4),=(-3,5),
=(-4,2),=(-5,1),
∴++=(-3,5)+(-4,2)+(-5,1)=(-12,8).……3分
根据平面向量基本定理,必存在唯一实数对m,n使得
++=m+n,
∴(-12,8)=m(1,3)+n(2,4).
∴,得m=32,n=-22.
∴++=32-22.……6分
25. (1) 证明 因为BC∥AD,AD 平面PAD,
BC 平面PAD,所以BC∥平面PAD.
又平面PAD∩平面PBC=l,BC 平面PBC,所以BC∥l.……3分
(2) 解 MN∥平面PAD.
证明如下:
如图所示,取DC的中点Q.连接MQ、NQ.
因为N为PC中点,所以NQ∥PD.
因为PD 平面PAD,NQ 平面PAD,所以NQ∥平面PAD.
同理MQ∥平面PAD.
又NQ 平面MNQ,MQ 平面MNQ,
NQ∩MQ=Q,所以平面MNQ∥平面PAD.
所以MN∥平面PAD.……6分
26.(1) 证明 把直线l的方程改写成(x+y-4)+m(2x+y-7)=0,
由方程组,解得,
所以直线l总过定点(3,1).
圆C的方程可写成(x-1)2+(y-2)2=25,所以圆C的圆心为(1,2),半径为5.
定点(3,1)到圆心(1,2)的距离为=<5,即点(3,1)在圆内.
所以过点(3,1)的直线总与圆相交,即不论m取什么实数,直线l与圆C总
相交.……3分
(2) 解 设直线与圆交于A、B两点.当直线l过定点M(3,1), 且垂直于过点M
的圆C的半径时,l被截得的弦长|AB|最短.
因为|AB|=2=2=2=4,
此时kAB=-=2,所以直线AB的方程为y-1=2(x-3),即2x-y-5=0.
故直线l被圆C截得的弦长最小值为4,此时直线l的方程为2x-y-5=0.
……6分
图1
正视图
俯视图
侧视图
5
5
6
3
5
5
6
3
数学模拟试卷(四)
第Ⅰ卷 (选择题,共48分)
一、选择题(本大题16小题,每小题3分,共48分。在下列各小题给出的四个选项中,只有一项是符合题目要求的。请将正确答案的序号填入下表。)
(1)已知集合,,则
A. B. C. D.
(2)已知角的终边过点P(-4,3), 则的值是
A. B. C. D.
(3)某几何体的三视图如图1所示,它的体积为
A. B. C. D.
(4) 某程序框图如图,该程序运行后输出的值是
A.-3 B.- C. D.2
在1 000mL的水中有一个草履虫,现从中随机取出2mL水样放到显微镜下
观察,则发现草履虫的概率
A.0 B.0.002 C.0.004 D.1
(6)已知锐角△ABC的面积为3,BC=4,CA=3,则角C的大小为
A.75° B.60° C.45° D.30°
已知以点A(2,-3)为圆心,半径长等于5的圆O,则点M(5,-7)与圆O
的位置关系是
A.在圆内 B.在圆上 C.在圆外 D.无法判断
(8)若直线过点(-1,-1),(2,2),则此直线的倾斜角是
A.30° B.45° C.60° D.90°
(9)函数图象的一条对称轴是
A.x轴 B.y轴 C.直线y=x D.直线x=0
(10)已知向量,,则向量与
A. 互相平行 B. 夹角为 C. 夹角为 D. 互相垂直
某林场有树苗2000棵,其中松树苗400棵.为调查树苗的生长情况,采
用分层抽样的方法抽取一个容量50的样本,则样本中松树苗的数量是
A.40 B.30 C.20 D.10
已知点P(x,y)在不等式组表示的平面区域上运动,
则z=x-y的取值范围是
A.[-2,-1] B.[-2,1 C.[-1,2] D.[1,2]
(13) 已知, 则的值为
A. B. 7 C. D.
(14)等比数列{an}中,a1+a2+a3+…+an=2n-1,则a12+a22+a32+…+an2等于
A B C D
设a、b∈R+,若a+b=1,则+的最小值等于
A.1 B.3 C.2 D.4
设是定义在上的函数,其图像关于原点对称,且当>0时,,则( )
A.1 B.-1 C. D.
第Ⅱ卷 (非选择题,共52分)
二、填空题(本大题共4小题,每小题4分,共16分。请将答案直接填在题中的横线上。)
17. 用二分法求方程x3-2x-5=0在区间[2,3]上的近似解,取区间中点x0=2.5,那么下一个有解区间为________.
有4所自主招生的大学,甲、乙两位同学各自选择其中一所学校参加考试,
若每位同学选择每所大学的可能性相同,则这两位同学选择同一所大学的概率为
________。
19. 两条直线l1:2x+3y-m=0与l2:x-my+12=0的交点在y轴上,那么m
的值为_________。
20. 已知函数f(x)=Asin(ωx+φ)(ω>0)的图象如图所示,则A+ω=________.
三、解答题(本大题共6小题,每小题6分,共36分。解答应写出文字说明,证明过程或者演算步骤。)
21.用单调性定义证明:函数在上是增函数。
22. 某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
(I)求回归直线方程=bx+a,其中b=-20,a=-b;
(II)预计在今后的销售中,销量与单价仍然服从(I)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
23.设Sn为数列{an}的前n项和,Sn=kn2+n,n∈N*,其中k是常数.
(1) 求a1及an;
(2) 若对于任意的m∈N*,am,a2m,a4m成等比数列,求k的值.
24. 已知函数f(x)=sin(x+)+cos(x-),x∈R.
(1)求f(x)的最小正周期和最小值;
(2)已知cos(β-α)=,cos(β+α)=-,0<α<β≤.
求证:[f(β)]2-2=0.
解:(1)∵f(x)=sin(x+-2π)+sin(x-+)
=sin(x-)+sin(x-)
=2sin(x-),
∴f(x)的最小正周期为T=2π,最小值为-2.
(2)证明:由已知得cos βcos α+sin βsin α=,
cos βcos α-sin βsin α=-.
两式相加得2cos βcos α=0.
∵0<α<β≤,∴β=.
∴[f(β)]2-2=4sin2-2=0.
25. 如图所示,P为平行四边形ABCD所在平面外一点,M、N分别为AB、PC的中点,平面PAD∩平面PBC=l.
(1) 求证:BC∥l;
(2) MN与平面PAD是否平行?试证明你的结论.
已知圆C:x2+y2-2x-4y-20=0及直线l:(2m+1)x+(m+1)y=7m+4
(m∈R).
(1) 证明:不论m取什么实数,直线l与圆C总相交;
(2) 求直线l被圆C截得的弦长的最小值及此时的直线方程.
高中学业水平考试数学模拟试卷(四)
参考答案
一、DDCDB BBBDA DCCDDB
二、17. [2,2.5] 18 . 19. m=±6 20.
三、21. 证明:任取则
……3分
又,即,
∴ 函数在上是增函数。……6分
22. 解:(I)
……3分
(II)工厂获得利润
当时,(元)……6分
23.解 (1) 由Sn=kn2+n,得a1=S1=k+1.
当n≥2时,an=Sn-Sn-1=2kn-k+1.
经验证,n=1时,上式也成立,
∴an=2kn-k+1.……3分
(2) ∵am,a2m,a4m成等比数列,∴a=am·a4m,
即(4mk-k+1)2=(2km-k+1)(8km-k+1),
整理得mk(k-1)=0.
∵对任意的m∈N*成立, ∴k=0或k=1.……6分
24. 解 ∵=(1,3),=(2,4),=(-3,5),
=(-4,2),=(-5,1),
∴++=(-3,5)+(-4,2)+(-5,1)=(-12,8).……3分
根据平面向量基本定理,必存在唯一实数对m,n使得
++=m+n,
∴(-12,8)=m(1,3)+n(2,4).
∴,得m=32,n=-22.
∴++=32-22.……6分
25. (1) 证明 因为BC∥AD,AD 平面PAD,
BC 平面PAD,所以BC∥平面PAD.
又平面PAD∩平面PBC=l,BC 平面PBC,所以BC∥l.……3分
(2) 解 MN∥平面PAD.
证明如下:
如图所示,取DC的中点Q.连接MQ、NQ.
因为N为PC中点,所以NQ∥PD.
因为PD 平面PAD,NQ 平面PAD,所以NQ∥平面PAD.
同理MQ∥平面PAD.
又NQ 平面MNQ,MQ 平面MNQ,
NQ∩MQ=Q,所以平面MNQ∥平面PAD.
所以MN∥平面PAD.……6分
26.(1) 证明 把直线l的方程改写成(x+y-4)+m(2x+y-7)=0,
由方程组,解得,
所以直线l总过定点(3,1).
圆C的方程可写成(x-1)2+(y-2)2=25,所以圆C的圆心为(1,2),半径为5.
定点(3,1)到圆心(1,2)的距离为=<5,即点(3,1)在圆内.
所以过点(3,1)的直线总与圆相交,即不论m取什么实数,直线l与圆C总
相交.……3分
(2) 解 设直线与圆交于A、B两点.当直线l过定点M(3,1), 且垂直于过点M
的圆C的半径时,l被截得的弦长|AB|最短.
因为|AB|=2=2=2=4,
此时kAB=-=2,所以直线AB的方程为y-1=2(x-3),即2x-y-5=0.
故直线l被圆C截得的弦长最小值为4,此时直线l的方程为2x-y-5=0.
……6分
图1
正视图
俯视图
侧视图
5
5
6
3
5
5
6
3
同课章节目录
