第6单元统计表和条形统计图(二)精选题(单元测试)数学五年级上册苏教版(含解析)
文档属性
| 名称 | 第6单元统计表和条形统计图(二)精选题(单元测试)数学五年级上册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-09 09:11:43 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第6单元统计表和条形统计图(二)精选题(单元测试)数学五年级上册苏教版
一、选择题
1.《国家学生体质健康标准》中指出,四年级男、女生1分钟跳绳的优秀标准分别是127个和135个。四(1)班20名男生平均跳了118个,15名女生平均跳了138个。根据以上信息,下列说法正确的是( )。
A.全体女生都达到优秀标准 B.每名女生的成绩都高于男生
C.全体男生的成绩未达到优秀标准 D.女生跳绳的整体水平高于优秀标准
2.下面的说法合理的是( )。
A.在一次捐款活动中,四(5)班平均每人捐50元,不可能有同学只捐5元
B.王鸣班上期末数学测试的平均分是91分,李刚班上期末数学测试的平均分是94分,李刚的数学成绩一定比王鸣高
C.校篮球队8名队员的平均体重是45千克。赵宝体重是48千克,他加入篮球队后,现在篮球队队员的平均体重比原来重
D.王刚身高160厘米,他到一个平均水深110厘米的池塘里游泳,不会有危险
3.一组平均数中,最大的数是28,这组数的平均数不可能是( )。
A.23 B.18 C.30
4.四(2)班第1组和第2组女生30秒跳绳成绩如下。
第1组女生30秒跳绳成绩统计表
成员 王芳 李玲 宋佳 赵萌 丁凡 孙静 合计
成绩/个 45 50 55 60 52 68 330
第2组女生30秒跳绳成绩统计表
成员 张颖 周舟 王瑶 吴雯 崔玲玲 合计
成绩/个 51 52 58 59 55 275
下面表述正确的是( )。
A.第1组比第2组平均成绩好 B.第2组比第1组平均成绩好
C.第1组和第2组平均成绩一样 D.无法判断
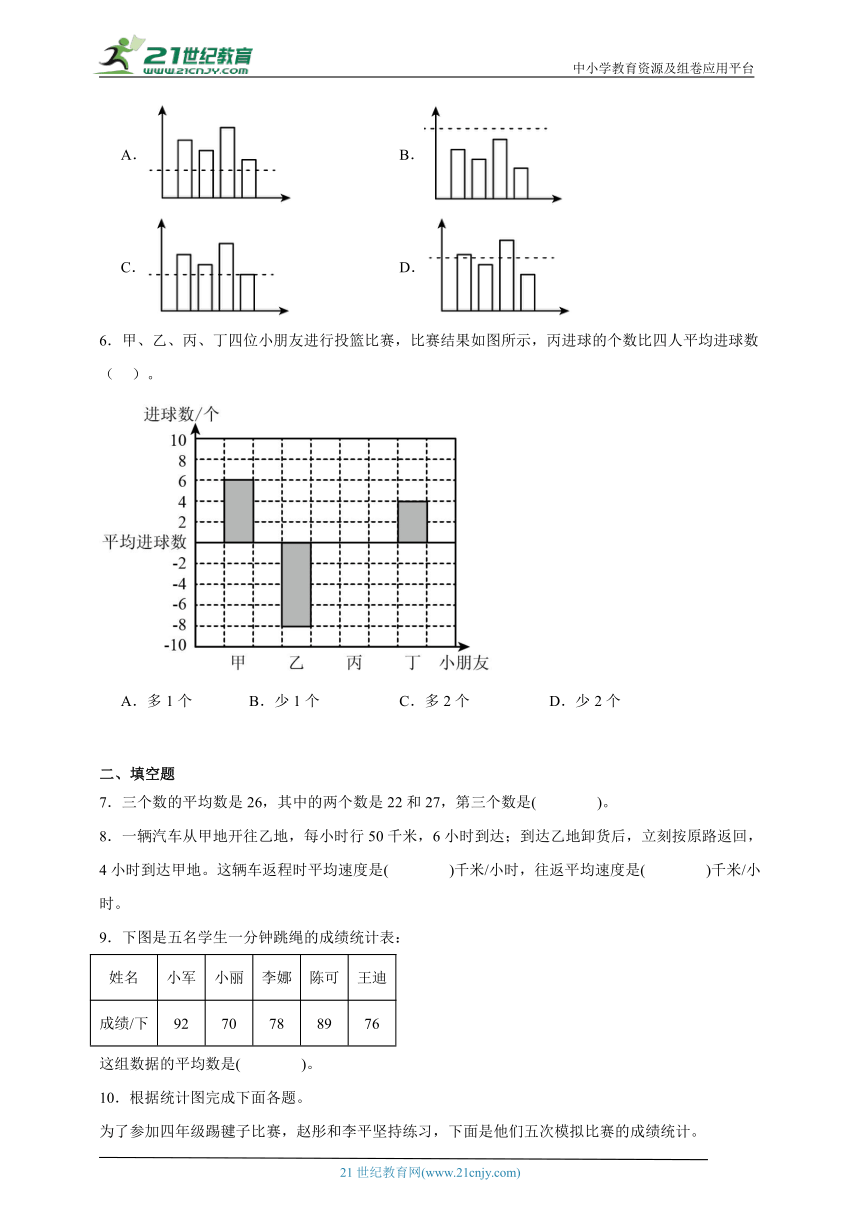
5.图中的虚线能正确代表所在图数据的平均数的是( )。
A. B.
C. D.
6.甲、乙、丙、丁四位小朋友进行投篮比赛,比赛结果如图所示,丙进球的个数比四人平均进球数( )。
A.多1个 B.少1个 C.多2个 D.少2个
二、填空题
7.三个数的平均数是26,其中的两个数是22和27,第三个数是( )。
8.一辆汽车从甲地开往乙地,每小时行50千米,6小时到达;到达乙地卸货后,立刻按原路返回,4小时到达甲地。这辆车返程时平均速度是( )千米/小时,往返平均速度是( )千米/小时。
9.下图是五名学生一分钟跳绳的成绩统计表:
姓名 小军 小丽 李娜 陈可 王迪
成绩/下 92 70 78 89 76
这组数据的平均数是( )。
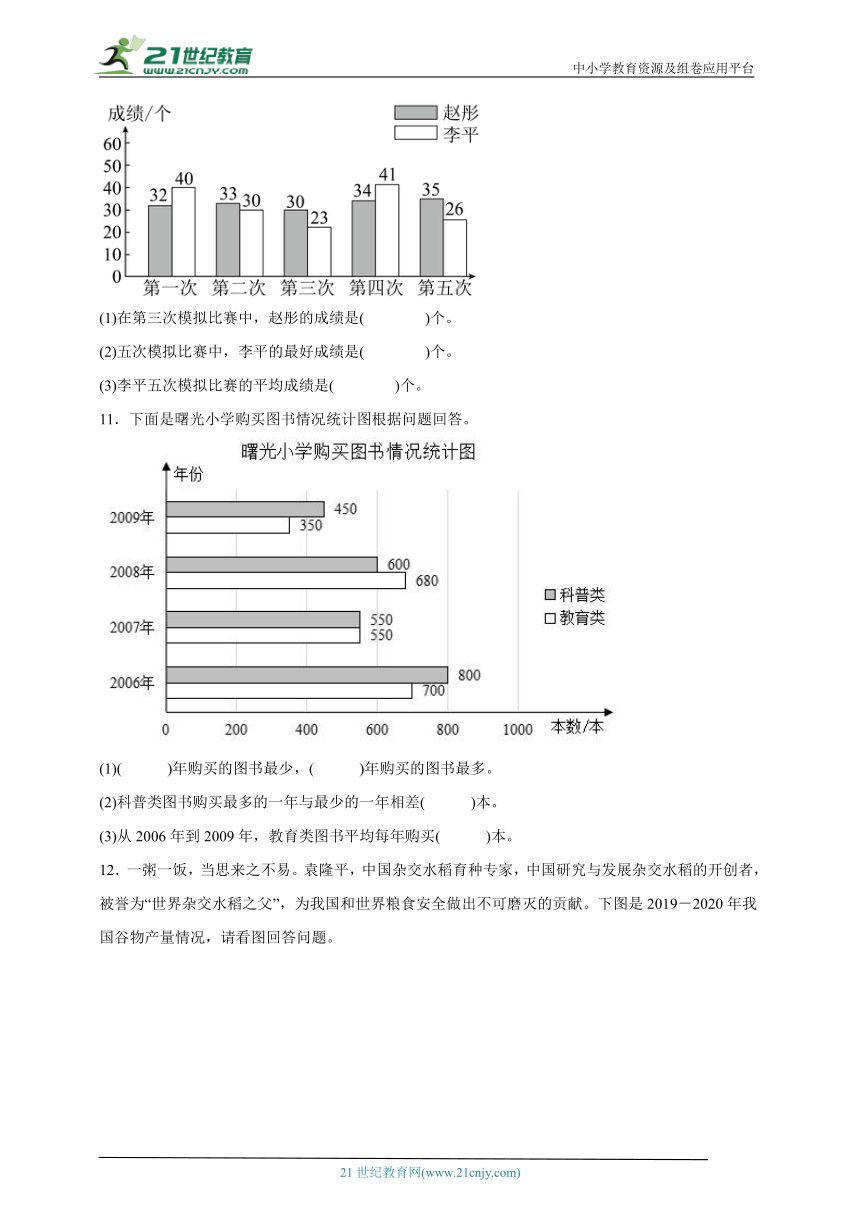
10.根据统计图完成下面各题。
为了参加四年级踢毽子比赛,赵彤和李平坚持练习,下面是他们五次模拟比赛的成绩统计。
(1)在第三次模拟比赛中,赵彤的成绩是( )个。
(2)五次模拟比赛中,李平的最好成绩是( )个。
(3)李平五次模拟比赛的平均成绩是( )个。
11.下面是曙光小学购买图书情况统计图根据问题回答。
(1)( )年购买的图书最少,( )年购买的图书最多。
(2)科普类图书购买最多的一年与最少的一年相差( )本。
(3)从2006年到2009年,教育类图书平均每年购买( )本。
12.一粥一饭,当思来之不易。袁隆平,中国杂交水稻育种专家,中国研究与发展杂交水稻的开创者,被誉为“世界杂交水稻之父”,为我国和世界粮食安全做出不可磨灭的贡献。下图是2019-2020年我国谷物产量情况,请看图回答问题。
(1)2019年我国谷物产量最高的品种是( )。
(2)2019-2020年这三种谷物中产量增长最多的品种是( ),它增长了( )万吨。
三、判断题
13.小林所在的小组同学的平均身高是150cm,小华所在的小组同学的平均身高是145cm,小林一定比小华高。( )
14.四年级同学平均每人捐款3.5元,其中聪聪一定捐了3元5角。( )
15.几个数的平均数是35,那么这几个数有的大于35,有的小于35,不可能有等于35的。( )
16.比较这次考试班与班成绩高低,应该选择平均数。( )
17.按照旅客的平均身高来订购新床,是比较合理的。( )
四、解答题
18.下面是实验小学三、四、五年级男、女生人数情况统计:
三年级 四年级 五年级
男生 33人 30人 40人
女生 27人 33人 35人
实验小学三、四、五年级男、女生人数情况统计图
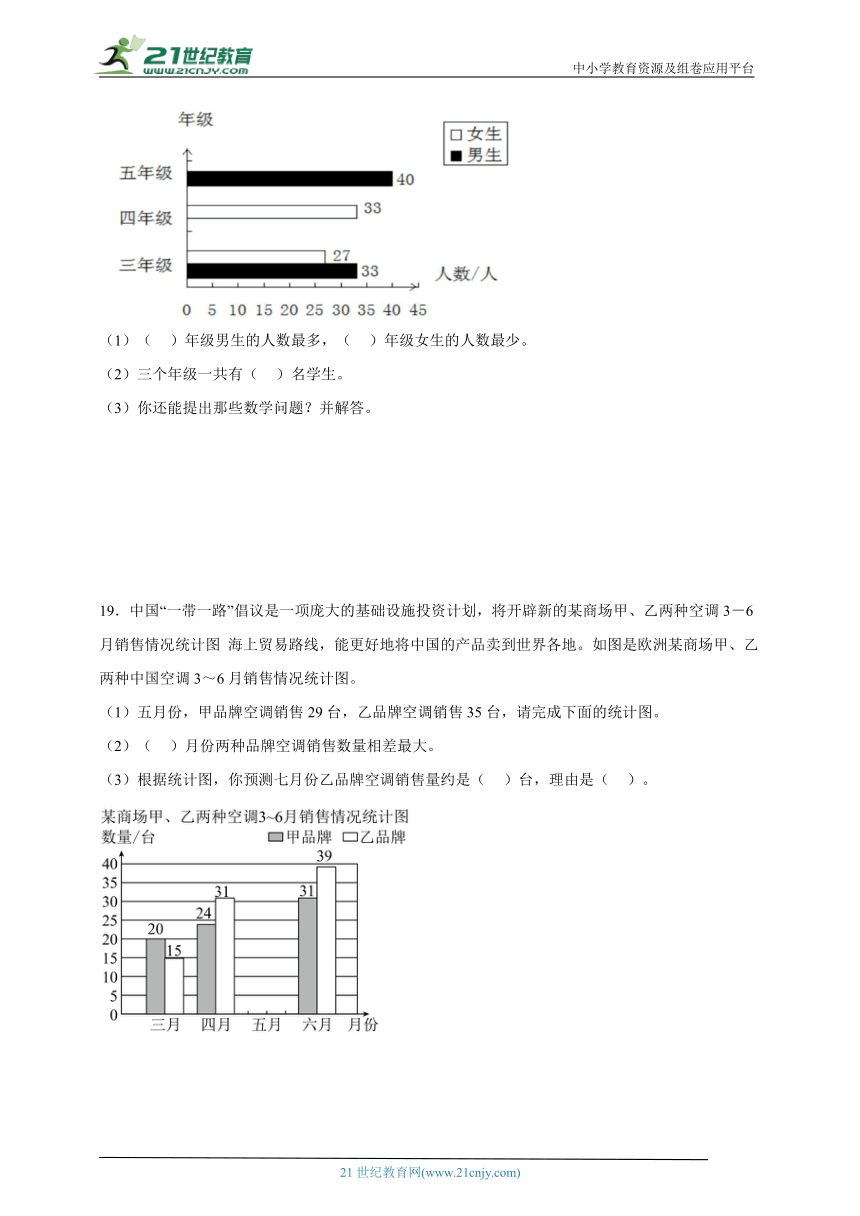
(1)( )年级男生的人数最多,( )年级女生的人数最少。
(2)三个年级一共有( )名学生。
(3)你还能提出那些数学问题?并解答。
19.中国“一带一路”倡议是一项庞大的基础设施投资计划,将开辟新的某商场甲、乙两种空调3-6月销售情况统计图 海上贸易路线,能更好地将中国的产品卖到世界各地。如图是欧洲某商场甲、乙两种中国空调3~6月销售情况统计图。
(1)五月份,甲品牌空调销售29台,乙品牌空调销售35台,请完成下面的统计图。
(2)( )月份两种品牌空调销售数量相差最大。
(3)根据统计图,你预测七月份乙品牌空调销售量约是( )台,理由是( )。
20.各式各样的卫星、飞船的发射离不开火箭,2017-2021年中国和俄罗斯火箭发射次数情况如表。
2017 2018 2019 2020 2021
中国 18 39 34 39 55
俄罗斯 20 20 25 17 25
(1)请根据统计表的数据完成统计图。
(2)这五年中,中国( )年火箭发射次数最多,( )年发射次数最少。
(3)这五年中,中国和俄罗斯( )年发射次数相差最多。
21.下图是小明家上半年的收支情况图。
小明家2022年上半年收支情况统计图
(1)小明家上半年( )月收支相等,( )月入不敷出。(“入不敷出”意思是收入比支出少)
(2)小明家( )月收支差距最大,相差( )元。
(3)上半年小明家平均每月收入多少元?
22.永辉超市打算在端午节期间再次采购一些粽子,为了更好地了解市场需求,该超市对近5天两种粽子的销售情况进行了数据统计,如下表。
永辉超市近5天两种粽子销售情况统计表
天数 第1天 第2天 第3天 第4天 第5天
鲜肉粽/千克 48 46 37 50 43
豆沙粽/千克 40 34 19 42 50
(1)根据统计表信息,补全上面的统计图(画出第4天)。
(2)两种粽子销售量相差最多的是第( )天。
(3)这5天豆沙粽平均每天销售( )千克。
(4)如果你是超市经理,你认为第6天怎样采购粽子比较合适?请写出理由。
参考答案:
1.D
【分析】根据平均数的意义,可知20名男生平均跳了118个,表示男生跳的平均数值,不能表示每个男生跳了118个;同理,15名女生平均跳了138个,表示女生跳的平均数值,不能表示每个女生都跳了138个。
【详解】118<127
138>135
男生跳绳的整体水平低于优秀标准;女生跳绳的整体水平高于优秀标准。
故答案为:D
2.C
【分析】根据平均数的意义,平均数只表示的是数据的平均值,实际的数据可能比平均数小,也可能比平均数大,据此逐项分析,找出合理的即可。
【详解】A.在一次捐款活动中,四(5)班平均每人捐50元,可能有同学只捐5元,原题说法不合理;
B.王鸣班上期末数学测试的平均分是91分,李刚班上期末数学测试的平均分是94分,李刚的数学成绩不一定比王鸣高,原题说法不合理;
C.校篮球队8名队员的平均体重是45千克。赵宝体重是48千克,他加入篮球队后,现在篮球队队员的平均体重比原来重,原题说法合理;
D.一个平均水深110厘米的池塘,可能有比160厘米深的地方,王刚身高160厘米,他到一个平均水深110厘米的池塘里游泳,是有一定危险的,原题说法不合理;
故答案为:C
【点睛】本题考查平均数的理解和应用,关键是要清楚平均数比一组数据的最小数要大,比最大数要小。
3.C
【分析】在一组数据中,平均数要比最小的数大,比最大的数小,据此解答。
【详解】一组平均数中,最大的数是28,这组数的平均数要比28小,所以这组数的平均数不可能是30。
故答案为:C
【点睛】明确平均数的含义是解题的关键。
4.C
【分析】平均数是表示一组数据的平均值,是指在一组数据中所有数据之和再除以这组数据的个数;依此分别计算出第1组和第2组女生30秒跳绳的平均成绩,然后再进行比较并选择即可。
【详解】330÷6=55(下)
275÷5=55(下)
55下=55下,由此可知,第1组和第2组平均成绩一样。
故答案为:C
【点睛】熟练掌握平均数的求法,是解答此题的关键。
5.D
【分析】平均数是指在一组数据中所有数据之和再除以数据的个数,平均数比最大数据小,比最小的数据大;据此对四幅图进行分析即可。
【详解】A.因为此图中虚线高度小于这组数据中最小的数,所以不符合题意;
B.因为此图中虚线的高度大于这组数据中最大的数,所以不符合题意;
C.因为此图中虚线的高度等于这组数据中最小的数,所以不符合题意;
D.因为此图中虚线的高度比这组数据中最大的数矮,比最小的数高,所以此图符合题意。
故答案为:D
【点睛】此题考查了平均数的含义,要注意观察图象。
6.D
【分析】甲的进球数比平均进球数多6个,乙的进球数比平均进球数少8个,丁的进球数比平均进球数多4个,即甲乙丁的进球数之和比平均进球数多2个,所以丙的进球数应比平均进球数少2个,据此解答。
【详解】甲的进球数比平均进球数多6个,乙的进球数比平均进球数少8个,丁的进球数比平均进球数多4个,甲乙丁的进球数之和是6+4-8=2(个)即比平均进球数多2个,所以丙的进球数应比平均进球数少2个。
故答案为:D
【点睛】考查应用平均数的知识分析图表,解决平均数问题,只要紧紧抓住平均数的数量关系式,找出总数量和对应的总份数即可。
7.29
【分析】根据平均数的意义和求法可知,这三个数之和除以3就是这三个数的平均数,三个数的平均数乘3就是这三个数之和,三个数之和减去其中的两个数就是第三个数。据此列式解答。
【详解】26×3=78
78-22-27
=56-27
=29
答:三个数的平均数是26,其中的两个数是22和27,第三个数是29。
8. 75 60
【分析】根据速度×时间=路程,即用50乘6即可求出甲地到乙地的路程,再根据路程÷时间=速度,用甲地到乙地的路程除以4即可求出这辆车返程时的平均速度;往返的平均速度=往返的路程÷往返的时间,据此进行计算即可。
【详解】50×6÷4
=300÷4
=75(千米/小时)
50×6×2÷(6+4)
=600÷10
=60(千米/小时)
则这辆车返程时平均速度是75千米/小时,往返平均速度是60千米/小时。
9.81
【分析】根据平均数=总数量÷个数,即用五名学生的总成绩除以5即可求解。
【详解】(92+70+78+89+76)÷5
=405÷5
=81(下)
则这组数据的平均数是81。
【点睛】本题考查求平均数,明确求平均数的方法是解题的关键。
10.(1)30
(2)41
(3)32
【分析】(1)在统计图的横轴上找到第三次比赛的直条,直条表示的成绩就是赵彤的成绩。
(2)在统计图上找出直条,最高的直条表示的成绩是李平的最好成绩。
(3)平均数=总数÷总份数,,据此将李平5次比赛的成绩相加,再除以5即可。
【详解】(1)在第三次模拟比赛中,赵彤的成绩是(30)个。
(2)五次模拟比赛中,李平的最好成绩是(41)个。
(3)(40+30+23+41+26)÷5
=(70+23+41+26)÷5
=(93+41+26)÷5
=(134+26)÷5
=160÷5
=32(个)
李平五次模拟比赛的平均成绩是(32)个。
【点睛】此题考查的目的是理解掌握复式条形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
11.(1) 2009 2006
(2)350
(3)570
【分析】(1)算出每年购买的图书的数量再比较即可;
(2)比较四年科普类图书的数量,用最多的一年的数量减去最少的一年的数量即可;
(3)将四年购买的教育图书的数量加起来算出四年购买的总本数,再用四年购买的总本数除以4即可。
【详解】(1)450+350=800(本)
600+680=1280(本)
550+550=1100(本)
800+700=1500(本)
1500>1280>1100>800
因此,2009年购买的图书最少,2006年购买的图书最多。
(2)450<550<600<800
800-450=350(本)
因此,科普类图书购买最多的一年与最少的一年相差350本。
(3)(350+680+550+700)÷4
=2280÷4
=570(本)
因此,从2006年到2009年,教育类图书平均每年购买570本。
【点睛】解决本题的关键是要理解掌握统计图的特点及作用和平均数的求法,并且能够根据统计图提供的信息,解决有关实际问题。
12.(1)玉米
(2) 稻谷 225
【分析】(1)2019年中,哪一个品种对应的条状最长,则这一年这个品种的产量就最高,依此填空。
(2)分别计算出2019-2020年每种谷物的重量差,然后再比较即可。
【详解】(1)根据统计图可知,2019年我国谷物产量最高的品种是玉米。
(2)稻谷:21186-20961=225(万吨)
小麦:13425-13359=66(万吨)
玉米:26067<26077,因此2019-2020年玉米的产量减少了。
225万吨>66万吨,即2019-2020年这三种谷物中产量增长最多的品种是稻谷,它增长了66万吨。
【点睛】熟练掌握复式条形统计图的特点,是解答此题的关键。
13.×
【分析】根据平均数的意义,平均数是反映一组数据的平均水平,平均数会受极端数据的影响,由此可知,小林所在小组同学的平均身高是150cm,小林的身高可能比150cm高一些,也可能比150cm矮一些;同理:小华所在小组同学的平均身高是145cm,小华的身高可能比145cm高一些,也可能比145cm矮一些;所以小林不一定比小华高,据此判断。
【详解】据分析可知:
小林所在小组同学的平均身高是150cm,小林的身高可能比150cm高一些,也可能比150cm矮一些;
小华所在小组同学的平均身高是145cm,小华的身高可能比145cm高一些,也可能比145cm矮一些;
所以小林不一定比小华高,故原题的说法错误。
故答案为:×
【点睛】此题考查的目的是理解掌握平均数的意义,明确:平均数会受偏大、偏小数据的影响。
14.×
【分析】平均数反映一组数据的平均情况,在一组数据中,有的数据可能会大于平均数,有的数据可能会小于平均数,有的数据可能会等于平均数。平均数大于一组数据的最小值,且小于这组数据的最大值。
【详解】四年级同学平均每人捐款3.5元,聪聪不一定捐了3元5角。
故答案为:×
【点睛】此题考查了平均数的性质和特点,要熟练掌握。
15.×
【分析】平均数是表示一组数据的平均值,是指在一组数据中所有数据之和再除以这组数据的个数;其特点是比最大数小,比最小数大;依此判断。
【详解】根据分析可知,几个数的平均数是35,那么这几个数有的大于35,有的小于35,可能有等于35的。
故答案为:×
【点睛】熟练掌握平均数的特点是解答此题的关键。
16.√
【分析】平均数表示一组数据的一般水平,用来比较班与班之间的成绩比较合适。
【详解】比较这次考试班与班成绩高低,应该选择平均数,说法正确。
故答案为:√。
【点睛】本题考查平均数,解答本题的关键是掌握平均数的概念。
17.×
【分析】平均数是反映一组数据的平均水平,并不能反映这组数据中各个数据的大小,据此解答。
【详解】旅客的平均身高,并不能反映出每一位旅客的身高,因为有的旅客的身高比平均身高要高一些, 睡这样的床就短了,所以这样并不合理。
故答案为:×
【点睛】此题考查了平均数的意义在实际生活中的灵活应用。
18.统计图见详解过程
(1)五;三
(2)198
(3)问题:五年级的学生人数比三年级的学生人数多多少人?15人(答案不唯一)
【分析】由统计图可得:纵坐标代表年级,横坐标代表人数,白色横直条代表女生人数,黑色横直条代表男生人数,根据表格中的数据,将统计图补充完整即可;
(1)根据条形统计图,看男生人数,哪个黑色条形最长,则表示哪个年级男生的人数最多;同理,看女生人数,哪个白色条形最短,则表示哪个年级女生的人数最少;
(2)将三个年级的男女生人数相加,即可求出三个年级一共有多少名学生;
(3)问题不唯一,符合题意即可。例如:五年级的学生人数比三年级的学生人数多多少人?分别求出五年级、三年级男女生的总人数,再作差即可。
【详解】实验小学三、四、五年级男、女生人数情况统计图
(1)五年级男生的人数最多,三年级女生的人数最少。
(2)(33+27)+(30+33)+(40+35)
=60+63+75
=123+75
=198(名)
三个年级一共有198名学生。
(3)问题:五年级的学生人数比三年级的学生人数多多少人?
(35+40)-(27+33)
=75-60
=15(人)
答:五年级的学生人数比三年级的学生人数多15人。(答案不唯一)
19.(1)见详解;(2)六;(3)43;理由见详解
【分析】(1)甲品牌的画成阴影的条形柱,在条形柱上标上数据29,乙品牌的画空白的条形柱,在条形柱上标上数据35即可;
(2)求出每个月份甲、乙两种品牌空调的数量差,再比较,根据比较结果来解答。
(3)六月、七月、八月空调的销量是比较好的,根据数据可知,五月比四月多几台,六月比五月多几台,根据这个数据来推测七月乙品牌空调的销量。
【详解】(1)如图:
(2)20-15=5(台)
31-24=7(台)
35-29=6(台)
39-31=8(台)
8>7>6>5
答:六月份两种品牌空调销售数量相差最大。
(3)39+4=43(台)
根据统计图,我预测七月份乙品牌空调销售量约是43台,理由是五月份比四月份多4台,六月份比五月份多4台,那么七月份比六月份多4台就是43台。
【点睛】本题主要考查复式条形统计图的应用,学会分析统计图是解题的关键,同时画图时注意图中1格表示多少台。
20.(1)见详解
(2)2021;2017
(3)2021
【分析】(1)制作条形统计图时先从列中找到项目,再从行中找到对应的数量高度画条形。复式统计图阴影空白条形分开表示。
(2)直接观察条形统计图,找出最长和最短的直条即可。
(3)求出相差数判断。
【详解】(1)如图:
(2)观察统计图,这五年中,中国2021年火箭发射次数最多,2017年发射次数最少。
(3)2017:20-18=2;
2018:39-20=19;
2019:34-25=9;
2020:39-17=22;
2021:55-25=30。
30最大,所以这五年中,中国和俄罗斯2021年发射次数相差最多。
【点睛】本题考查条形统计图相关知识,学会填补条形统计图,并熟练的运用统计图分析数据关系。
21.(1)2;6
(2)3;2600元
(3)5100元
【分析】(1)根据条形统计图,找出收支相等的月份以及收入小于支出的月份。
(2)分别求出各个月份的收支差距,再比较大小解答。
(3)将1~6月份的收入相加,再除以6,求出上半年小明家平均每月收入。
【详解】(1)小明家上半年2月收支相等,6月入不敷出。
(2)5000-4000=1000(元)
4000-4000=0(元)
7000-4400=2600(元)
5600-3600=2000(元)
5200-4800=400(元)
4800-3800=1000(元)
2600>1000>800>400>0
小明家3月收支差距最大,相差2600元。
(3)(5000+4000+7000+5600+5200+3800)÷6
=30600÷6
=5100(元)
答:上半年小明家平均每月收入5100元。
【点睛】此题考査的目的是理解掌握统计图的特点及作用,以及平均数的求法,能够根据统计图提供的信息,解决有关的实际问题。平均数问题的解题关键是确定总数量及其对应的份数。
22.(1)见详解;(2)3;(3)37;
(4)多采购豆沙粽,比第5天少采购鲜肉粽。因为从第3天起,豆沙粽的销量在逐渐增加,而第5天的销量比第4天、第1天和第2天的销量都少。(答案不唯一)
【分析】(1)根据复式条形统计图的特点,并结合复式统计表中的信息补全统计图即可。
(2)分别计算出每一天中两种粽子的销量差,然后再比较即可。
(3)平均数是表示一组数据的平均值,是指在一组数据中所有数据之和再除以这组数据的个数;依此计算。
(4)根据两种粽子销量的变化趋势进行解答,言之合理即可。
【详解】(1)画图如下:
(2)48-40=8(千克)
46-34=12(千克)
37-19=18(千克)
50-42=8(千克)
50-43=7(千克)
18>12>8>7
两种粽子销售量相差最多的是第3天。
(3)(40+34+19+42+50)÷5
=185÷5
=37(千克)
这5天豆沙粽平均每天销售37千克。
(4)如果我是超市经理,我认为第6天多采购豆沙粽,比第5天少采购鲜肉粽。因为从第3天起,豆沙粽的销量在逐渐增加,而第5天的销量比第4天、第1天和第2天的销量都少。
【点睛】解答此题的关键是应熟练掌握复式条形统计图的绘制方法及应用,以及平均数的求法,并且能够根据统计图提供的信息,解决有关的实际问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第6单元统计表和条形统计图(二)精选题(单元测试)数学五年级上册苏教版
一、选择题
1.《国家学生体质健康标准》中指出,四年级男、女生1分钟跳绳的优秀标准分别是127个和135个。四(1)班20名男生平均跳了118个,15名女生平均跳了138个。根据以上信息,下列说法正确的是( )。
A.全体女生都达到优秀标准 B.每名女生的成绩都高于男生
C.全体男生的成绩未达到优秀标准 D.女生跳绳的整体水平高于优秀标准
2.下面的说法合理的是( )。
A.在一次捐款活动中,四(5)班平均每人捐50元,不可能有同学只捐5元
B.王鸣班上期末数学测试的平均分是91分,李刚班上期末数学测试的平均分是94分,李刚的数学成绩一定比王鸣高
C.校篮球队8名队员的平均体重是45千克。赵宝体重是48千克,他加入篮球队后,现在篮球队队员的平均体重比原来重
D.王刚身高160厘米,他到一个平均水深110厘米的池塘里游泳,不会有危险
3.一组平均数中,最大的数是28,这组数的平均数不可能是( )。
A.23 B.18 C.30
4.四(2)班第1组和第2组女生30秒跳绳成绩如下。
第1组女生30秒跳绳成绩统计表
成员 王芳 李玲 宋佳 赵萌 丁凡 孙静 合计
成绩/个 45 50 55 60 52 68 330
第2组女生30秒跳绳成绩统计表
成员 张颖 周舟 王瑶 吴雯 崔玲玲 合计
成绩/个 51 52 58 59 55 275
下面表述正确的是( )。
A.第1组比第2组平均成绩好 B.第2组比第1组平均成绩好
C.第1组和第2组平均成绩一样 D.无法判断
5.图中的虚线能正确代表所在图数据的平均数的是( )。
A. B.
C. D.
6.甲、乙、丙、丁四位小朋友进行投篮比赛,比赛结果如图所示,丙进球的个数比四人平均进球数( )。
A.多1个 B.少1个 C.多2个 D.少2个
二、填空题
7.三个数的平均数是26,其中的两个数是22和27,第三个数是( )。
8.一辆汽车从甲地开往乙地,每小时行50千米,6小时到达;到达乙地卸货后,立刻按原路返回,4小时到达甲地。这辆车返程时平均速度是( )千米/小时,往返平均速度是( )千米/小时。
9.下图是五名学生一分钟跳绳的成绩统计表:
姓名 小军 小丽 李娜 陈可 王迪
成绩/下 92 70 78 89 76
这组数据的平均数是( )。
10.根据统计图完成下面各题。
为了参加四年级踢毽子比赛,赵彤和李平坚持练习,下面是他们五次模拟比赛的成绩统计。
(1)在第三次模拟比赛中,赵彤的成绩是( )个。
(2)五次模拟比赛中,李平的最好成绩是( )个。
(3)李平五次模拟比赛的平均成绩是( )个。
11.下面是曙光小学购买图书情况统计图根据问题回答。
(1)( )年购买的图书最少,( )年购买的图书最多。
(2)科普类图书购买最多的一年与最少的一年相差( )本。
(3)从2006年到2009年,教育类图书平均每年购买( )本。
12.一粥一饭,当思来之不易。袁隆平,中国杂交水稻育种专家,中国研究与发展杂交水稻的开创者,被誉为“世界杂交水稻之父”,为我国和世界粮食安全做出不可磨灭的贡献。下图是2019-2020年我国谷物产量情况,请看图回答问题。
(1)2019年我国谷物产量最高的品种是( )。
(2)2019-2020年这三种谷物中产量增长最多的品种是( ),它增长了( )万吨。
三、判断题
13.小林所在的小组同学的平均身高是150cm,小华所在的小组同学的平均身高是145cm,小林一定比小华高。( )
14.四年级同学平均每人捐款3.5元,其中聪聪一定捐了3元5角。( )
15.几个数的平均数是35,那么这几个数有的大于35,有的小于35,不可能有等于35的。( )
16.比较这次考试班与班成绩高低,应该选择平均数。( )
17.按照旅客的平均身高来订购新床,是比较合理的。( )
四、解答题
18.下面是实验小学三、四、五年级男、女生人数情况统计:
三年级 四年级 五年级
男生 33人 30人 40人
女生 27人 33人 35人
实验小学三、四、五年级男、女生人数情况统计图
(1)( )年级男生的人数最多,( )年级女生的人数最少。
(2)三个年级一共有( )名学生。
(3)你还能提出那些数学问题?并解答。
19.中国“一带一路”倡议是一项庞大的基础设施投资计划,将开辟新的某商场甲、乙两种空调3-6月销售情况统计图 海上贸易路线,能更好地将中国的产品卖到世界各地。如图是欧洲某商场甲、乙两种中国空调3~6月销售情况统计图。
(1)五月份,甲品牌空调销售29台,乙品牌空调销售35台,请完成下面的统计图。
(2)( )月份两种品牌空调销售数量相差最大。
(3)根据统计图,你预测七月份乙品牌空调销售量约是( )台,理由是( )。
20.各式各样的卫星、飞船的发射离不开火箭,2017-2021年中国和俄罗斯火箭发射次数情况如表。
2017 2018 2019 2020 2021
中国 18 39 34 39 55
俄罗斯 20 20 25 17 25
(1)请根据统计表的数据完成统计图。
(2)这五年中,中国( )年火箭发射次数最多,( )年发射次数最少。
(3)这五年中,中国和俄罗斯( )年发射次数相差最多。
21.下图是小明家上半年的收支情况图。
小明家2022年上半年收支情况统计图
(1)小明家上半年( )月收支相等,( )月入不敷出。(“入不敷出”意思是收入比支出少)
(2)小明家( )月收支差距最大,相差( )元。
(3)上半年小明家平均每月收入多少元?
22.永辉超市打算在端午节期间再次采购一些粽子,为了更好地了解市场需求,该超市对近5天两种粽子的销售情况进行了数据统计,如下表。
永辉超市近5天两种粽子销售情况统计表
天数 第1天 第2天 第3天 第4天 第5天
鲜肉粽/千克 48 46 37 50 43
豆沙粽/千克 40 34 19 42 50
(1)根据统计表信息,补全上面的统计图(画出第4天)。
(2)两种粽子销售量相差最多的是第( )天。
(3)这5天豆沙粽平均每天销售( )千克。
(4)如果你是超市经理,你认为第6天怎样采购粽子比较合适?请写出理由。
参考答案:
1.D
【分析】根据平均数的意义,可知20名男生平均跳了118个,表示男生跳的平均数值,不能表示每个男生跳了118个;同理,15名女生平均跳了138个,表示女生跳的平均数值,不能表示每个女生都跳了138个。
【详解】118<127
138>135
男生跳绳的整体水平低于优秀标准;女生跳绳的整体水平高于优秀标准。
故答案为:D
2.C
【分析】根据平均数的意义,平均数只表示的是数据的平均值,实际的数据可能比平均数小,也可能比平均数大,据此逐项分析,找出合理的即可。
【详解】A.在一次捐款活动中,四(5)班平均每人捐50元,可能有同学只捐5元,原题说法不合理;
B.王鸣班上期末数学测试的平均分是91分,李刚班上期末数学测试的平均分是94分,李刚的数学成绩不一定比王鸣高,原题说法不合理;
C.校篮球队8名队员的平均体重是45千克。赵宝体重是48千克,他加入篮球队后,现在篮球队队员的平均体重比原来重,原题说法合理;
D.一个平均水深110厘米的池塘,可能有比160厘米深的地方,王刚身高160厘米,他到一个平均水深110厘米的池塘里游泳,是有一定危险的,原题说法不合理;
故答案为:C
【点睛】本题考查平均数的理解和应用,关键是要清楚平均数比一组数据的最小数要大,比最大数要小。
3.C
【分析】在一组数据中,平均数要比最小的数大,比最大的数小,据此解答。
【详解】一组平均数中,最大的数是28,这组数的平均数要比28小,所以这组数的平均数不可能是30。
故答案为:C
【点睛】明确平均数的含义是解题的关键。
4.C
【分析】平均数是表示一组数据的平均值,是指在一组数据中所有数据之和再除以这组数据的个数;依此分别计算出第1组和第2组女生30秒跳绳的平均成绩,然后再进行比较并选择即可。
【详解】330÷6=55(下)
275÷5=55(下)
55下=55下,由此可知,第1组和第2组平均成绩一样。
故答案为:C
【点睛】熟练掌握平均数的求法,是解答此题的关键。
5.D
【分析】平均数是指在一组数据中所有数据之和再除以数据的个数,平均数比最大数据小,比最小的数据大;据此对四幅图进行分析即可。
【详解】A.因为此图中虚线高度小于这组数据中最小的数,所以不符合题意;
B.因为此图中虚线的高度大于这组数据中最大的数,所以不符合题意;
C.因为此图中虚线的高度等于这组数据中最小的数,所以不符合题意;
D.因为此图中虚线的高度比这组数据中最大的数矮,比最小的数高,所以此图符合题意。
故答案为:D
【点睛】此题考查了平均数的含义,要注意观察图象。
6.D
【分析】甲的进球数比平均进球数多6个,乙的进球数比平均进球数少8个,丁的进球数比平均进球数多4个,即甲乙丁的进球数之和比平均进球数多2个,所以丙的进球数应比平均进球数少2个,据此解答。
【详解】甲的进球数比平均进球数多6个,乙的进球数比平均进球数少8个,丁的进球数比平均进球数多4个,甲乙丁的进球数之和是6+4-8=2(个)即比平均进球数多2个,所以丙的进球数应比平均进球数少2个。
故答案为:D
【点睛】考查应用平均数的知识分析图表,解决平均数问题,只要紧紧抓住平均数的数量关系式,找出总数量和对应的总份数即可。
7.29
【分析】根据平均数的意义和求法可知,这三个数之和除以3就是这三个数的平均数,三个数的平均数乘3就是这三个数之和,三个数之和减去其中的两个数就是第三个数。据此列式解答。
【详解】26×3=78
78-22-27
=56-27
=29
答:三个数的平均数是26,其中的两个数是22和27,第三个数是29。
8. 75 60
【分析】根据速度×时间=路程,即用50乘6即可求出甲地到乙地的路程,再根据路程÷时间=速度,用甲地到乙地的路程除以4即可求出这辆车返程时的平均速度;往返的平均速度=往返的路程÷往返的时间,据此进行计算即可。
【详解】50×6÷4
=300÷4
=75(千米/小时)
50×6×2÷(6+4)
=600÷10
=60(千米/小时)
则这辆车返程时平均速度是75千米/小时,往返平均速度是60千米/小时。
9.81
【分析】根据平均数=总数量÷个数,即用五名学生的总成绩除以5即可求解。
【详解】(92+70+78+89+76)÷5
=405÷5
=81(下)
则这组数据的平均数是81。
【点睛】本题考查求平均数,明确求平均数的方法是解题的关键。
10.(1)30
(2)41
(3)32
【分析】(1)在统计图的横轴上找到第三次比赛的直条,直条表示的成绩就是赵彤的成绩。
(2)在统计图上找出直条,最高的直条表示的成绩是李平的最好成绩。
(3)平均数=总数÷总份数,,据此将李平5次比赛的成绩相加,再除以5即可。
【详解】(1)在第三次模拟比赛中,赵彤的成绩是(30)个。
(2)五次模拟比赛中,李平的最好成绩是(41)个。
(3)(40+30+23+41+26)÷5
=(70+23+41+26)÷5
=(93+41+26)÷5
=(134+26)÷5
=160÷5
=32(个)
李平五次模拟比赛的平均成绩是(32)个。
【点睛】此题考查的目的是理解掌握复式条形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
11.(1) 2009 2006
(2)350
(3)570
【分析】(1)算出每年购买的图书的数量再比较即可;
(2)比较四年科普类图书的数量,用最多的一年的数量减去最少的一年的数量即可;
(3)将四年购买的教育图书的数量加起来算出四年购买的总本数,再用四年购买的总本数除以4即可。
【详解】(1)450+350=800(本)
600+680=1280(本)
550+550=1100(本)
800+700=1500(本)
1500>1280>1100>800
因此,2009年购买的图书最少,2006年购买的图书最多。
(2)450<550<600<800
800-450=350(本)
因此,科普类图书购买最多的一年与最少的一年相差350本。
(3)(350+680+550+700)÷4
=2280÷4
=570(本)
因此,从2006年到2009年,教育类图书平均每年购买570本。
【点睛】解决本题的关键是要理解掌握统计图的特点及作用和平均数的求法,并且能够根据统计图提供的信息,解决有关实际问题。
12.(1)玉米
(2) 稻谷 225
【分析】(1)2019年中,哪一个品种对应的条状最长,则这一年这个品种的产量就最高,依此填空。
(2)分别计算出2019-2020年每种谷物的重量差,然后再比较即可。
【详解】(1)根据统计图可知,2019年我国谷物产量最高的品种是玉米。
(2)稻谷:21186-20961=225(万吨)
小麦:13425-13359=66(万吨)
玉米:26067<26077,因此2019-2020年玉米的产量减少了。
225万吨>66万吨,即2019-2020年这三种谷物中产量增长最多的品种是稻谷,它增长了66万吨。
【点睛】熟练掌握复式条形统计图的特点,是解答此题的关键。
13.×
【分析】根据平均数的意义,平均数是反映一组数据的平均水平,平均数会受极端数据的影响,由此可知,小林所在小组同学的平均身高是150cm,小林的身高可能比150cm高一些,也可能比150cm矮一些;同理:小华所在小组同学的平均身高是145cm,小华的身高可能比145cm高一些,也可能比145cm矮一些;所以小林不一定比小华高,据此判断。
【详解】据分析可知:
小林所在小组同学的平均身高是150cm,小林的身高可能比150cm高一些,也可能比150cm矮一些;
小华所在小组同学的平均身高是145cm,小华的身高可能比145cm高一些,也可能比145cm矮一些;
所以小林不一定比小华高,故原题的说法错误。
故答案为:×
【点睛】此题考查的目的是理解掌握平均数的意义,明确:平均数会受偏大、偏小数据的影响。
14.×
【分析】平均数反映一组数据的平均情况,在一组数据中,有的数据可能会大于平均数,有的数据可能会小于平均数,有的数据可能会等于平均数。平均数大于一组数据的最小值,且小于这组数据的最大值。
【详解】四年级同学平均每人捐款3.5元,聪聪不一定捐了3元5角。
故答案为:×
【点睛】此题考查了平均数的性质和特点,要熟练掌握。
15.×
【分析】平均数是表示一组数据的平均值,是指在一组数据中所有数据之和再除以这组数据的个数;其特点是比最大数小,比最小数大;依此判断。
【详解】根据分析可知,几个数的平均数是35,那么这几个数有的大于35,有的小于35,可能有等于35的。
故答案为:×
【点睛】熟练掌握平均数的特点是解答此题的关键。
16.√
【分析】平均数表示一组数据的一般水平,用来比较班与班之间的成绩比较合适。
【详解】比较这次考试班与班成绩高低,应该选择平均数,说法正确。
故答案为:√。
【点睛】本题考查平均数,解答本题的关键是掌握平均数的概念。
17.×
【分析】平均数是反映一组数据的平均水平,并不能反映这组数据中各个数据的大小,据此解答。
【详解】旅客的平均身高,并不能反映出每一位旅客的身高,因为有的旅客的身高比平均身高要高一些, 睡这样的床就短了,所以这样并不合理。
故答案为:×
【点睛】此题考查了平均数的意义在实际生活中的灵活应用。
18.统计图见详解过程
(1)五;三
(2)198
(3)问题:五年级的学生人数比三年级的学生人数多多少人?15人(答案不唯一)
【分析】由统计图可得:纵坐标代表年级,横坐标代表人数,白色横直条代表女生人数,黑色横直条代表男生人数,根据表格中的数据,将统计图补充完整即可;
(1)根据条形统计图,看男生人数,哪个黑色条形最长,则表示哪个年级男生的人数最多;同理,看女生人数,哪个白色条形最短,则表示哪个年级女生的人数最少;
(2)将三个年级的男女生人数相加,即可求出三个年级一共有多少名学生;
(3)问题不唯一,符合题意即可。例如:五年级的学生人数比三年级的学生人数多多少人?分别求出五年级、三年级男女生的总人数,再作差即可。
【详解】实验小学三、四、五年级男、女生人数情况统计图
(1)五年级男生的人数最多,三年级女生的人数最少。
(2)(33+27)+(30+33)+(40+35)
=60+63+75
=123+75
=198(名)
三个年级一共有198名学生。
(3)问题:五年级的学生人数比三年级的学生人数多多少人?
(35+40)-(27+33)
=75-60
=15(人)
答:五年级的学生人数比三年级的学生人数多15人。(答案不唯一)
19.(1)见详解;(2)六;(3)43;理由见详解
【分析】(1)甲品牌的画成阴影的条形柱,在条形柱上标上数据29,乙品牌的画空白的条形柱,在条形柱上标上数据35即可;
(2)求出每个月份甲、乙两种品牌空调的数量差,再比较,根据比较结果来解答。
(3)六月、七月、八月空调的销量是比较好的,根据数据可知,五月比四月多几台,六月比五月多几台,根据这个数据来推测七月乙品牌空调的销量。
【详解】(1)如图:
(2)20-15=5(台)
31-24=7(台)
35-29=6(台)
39-31=8(台)
8>7>6>5
答:六月份两种品牌空调销售数量相差最大。
(3)39+4=43(台)
根据统计图,我预测七月份乙品牌空调销售量约是43台,理由是五月份比四月份多4台,六月份比五月份多4台,那么七月份比六月份多4台就是43台。
【点睛】本题主要考查复式条形统计图的应用,学会分析统计图是解题的关键,同时画图时注意图中1格表示多少台。
20.(1)见详解
(2)2021;2017
(3)2021
【分析】(1)制作条形统计图时先从列中找到项目,再从行中找到对应的数量高度画条形。复式统计图阴影空白条形分开表示。
(2)直接观察条形统计图,找出最长和最短的直条即可。
(3)求出相差数判断。
【详解】(1)如图:
(2)观察统计图,这五年中,中国2021年火箭发射次数最多,2017年发射次数最少。
(3)2017:20-18=2;
2018:39-20=19;
2019:34-25=9;
2020:39-17=22;
2021:55-25=30。
30最大,所以这五年中,中国和俄罗斯2021年发射次数相差最多。
【点睛】本题考查条形统计图相关知识,学会填补条形统计图,并熟练的运用统计图分析数据关系。
21.(1)2;6
(2)3;2600元
(3)5100元
【分析】(1)根据条形统计图,找出收支相等的月份以及收入小于支出的月份。
(2)分别求出各个月份的收支差距,再比较大小解答。
(3)将1~6月份的收入相加,再除以6,求出上半年小明家平均每月收入。
【详解】(1)小明家上半年2月收支相等,6月入不敷出。
(2)5000-4000=1000(元)
4000-4000=0(元)
7000-4400=2600(元)
5600-3600=2000(元)
5200-4800=400(元)
4800-3800=1000(元)
2600>1000>800>400>0
小明家3月收支差距最大,相差2600元。
(3)(5000+4000+7000+5600+5200+3800)÷6
=30600÷6
=5100(元)
答:上半年小明家平均每月收入5100元。
【点睛】此题考査的目的是理解掌握统计图的特点及作用,以及平均数的求法,能够根据统计图提供的信息,解决有关的实际问题。平均数问题的解题关键是确定总数量及其对应的份数。
22.(1)见详解;(2)3;(3)37;
(4)多采购豆沙粽,比第5天少采购鲜肉粽。因为从第3天起,豆沙粽的销量在逐渐增加,而第5天的销量比第4天、第1天和第2天的销量都少。(答案不唯一)
【分析】(1)根据复式条形统计图的特点,并结合复式统计表中的信息补全统计图即可。
(2)分别计算出每一天中两种粽子的销量差,然后再比较即可。
(3)平均数是表示一组数据的平均值,是指在一组数据中所有数据之和再除以这组数据的个数;依此计算。
(4)根据两种粽子销量的变化趋势进行解答,言之合理即可。
【详解】(1)画图如下:
(2)48-40=8(千克)
46-34=12(千克)
37-19=18(千克)
50-42=8(千克)
50-43=7(千克)
18>12>8>7
两种粽子销售量相差最多的是第3天。
(3)(40+34+19+42+50)÷5
=185÷5
=37(千克)
这5天豆沙粽平均每天销售37千克。
(4)如果我是超市经理,我认为第6天多采购豆沙粽,比第5天少采购鲜肉粽。因为从第3天起,豆沙粽的销量在逐渐增加,而第5天的销量比第4天、第1天和第2天的销量都少。
【点睛】解答此题的关键是应熟练掌握复式条形统计图的绘制方法及应用,以及平均数的求法,并且能够根据统计图提供的信息,解决有关的实际问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
