第一章轴对称图形单元测试(无答案)(南门中学苏科版八年级数学)
文档属性
| 名称 | 第一章轴对称图形单元测试(无答案)(南门中学苏科版八年级数学) |
|
|
| 格式 | rar | ||
| 文件大小 | 334.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-24 00:00:00 | ||
图片预览


文档简介
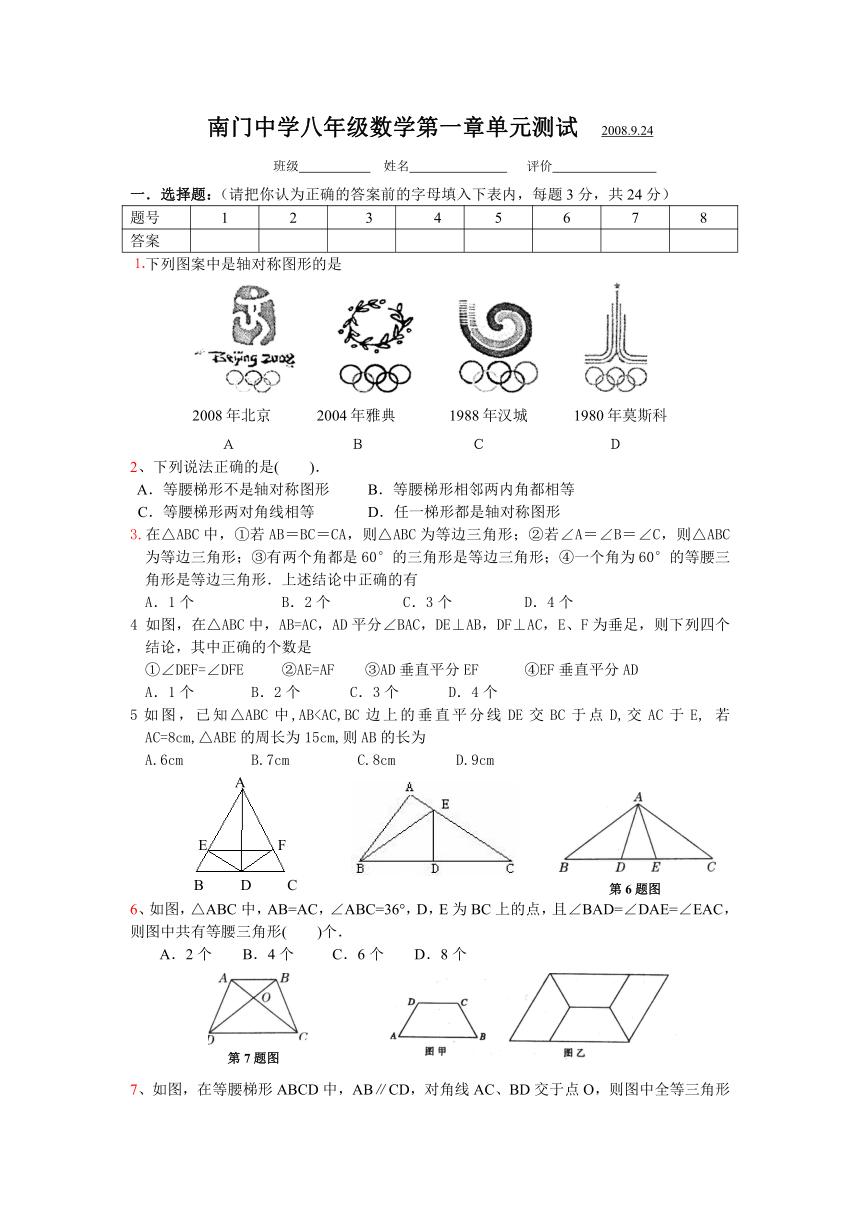
南门中学八年级数学第一章单元测试 2008.9.24
班级 姓名 评价
一.选择题:(请把你认为正确的答案前的字母填入下表内,每题3分,共24分)
题号 1 2 3 4 5 6 7 8
答案
⒈下列图案中是轴对称图形的是
A B C D
2、下列说法正确的是( ).
A.等腰梯形不是轴对称图形 B.等腰梯形相邻两内角都相等
C.等腰梯形两对角线相等 D.任一梯形都是轴对称图形
3.在△ABC中,①若AB=BC=CA,则△ABC为等边三角形;②若∠A=∠B=∠C,则△ABC为等边三角形;③有两个角都是60°的三角形是等边三角形;④一个角为60°的等腰三角形是等边三角形.上述结论中正确的有
A.1个 B.2个 C.3个 D.4个
4 如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,则下列四个结论,其中正确的个数是
①∠DEF=∠DFE ②AE=AF ③AD垂直平分EF ④EF垂直平分AD
A.1个 B.2个 C.3个 D.4个
5如图,已知△ABC中,ABA.6cm B.7cm C.8cm D.9cm
6、如图,△ABC中,AB=AC,∠ABC=36°,D,E为BC上的点,且∠BAD=∠DAE=∠EAC,则图中共有等腰三角形( )个.
A.2个 B.4个 C.6个 D.8个
7、如图,在等腰梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则图中全等三角形有( ). A.1对 B.2对 C.3对 D.4对
8. 如图甲,四边形ABCD是等腰梯形,AB∥DC.由4个这样的等腰梯形可以拼出图乙所示的平行四边形,则∠A的度数为( )A.50° B. 60° C. 70° D. 80°
二.填空题:(每题3分,共24分)
1等腰三角形的一个外角为110°,则它的另两个角是____ ____.
2、(1)如图,由Rt△CDE≌Rt△ACF,可得∠DCE+∠ACF= °,从而∠ACB= °.
(2)设小方格的边长为1,则AB= ;
(3)取AB的中点M,连接CM.则CM= ,理由是: .
3、如图,△ABC中,AB=AC,D是BC的中点,A C的垂直平分线EF分别交A C、AD、AB于点E、F、G.那么,点F到△ABC的边 的距离相等,点F到△ABC
的顶点 的距离相等.
4、代号为①、②、③、④的4张三角形纸片都有一个角为50°.如果它们另有一个角分别为50°、70°、80°、90°,那么其中只有代号为 的纸片能沿直线剪一刀得到等腰梯形.
5、如图,在梯形ABCD中,AD∥BC,DE∥AB,AD=4 cm,△DEC的周长为12 cm,则BE= ,梯形ABCD的周长= .
7、如图,已知中,,,直角的顶点是 中点,两边,分别交,于点,,给出以下四个结论:①,② ,③是等腰直角三角形,④。当在内绕顶点旋转时(点不与,重合),上述结论中始终正确的序号有 .
8.如图,∠AOB是一钢架,且∠AOB=10°,为了使钢架更加坚固,需在其内部添加一些钢管EF,FG,GH:……添加的钢管长度都与0E相等,则最多能添这样的钢管 根.
三.解答题:(本大题共8题,共52分)
1、(4分)利用图中的网格线,分别以线段MN和PQ为一底,画一个底角为45°的等腰梯形,且使它的另外2个顶点也在格点上.
2、(6分)如图,△ABC和△关于直线MN对称,△和△关于直线EF对称.
(1)画出直线EF;
(2)直线MN与EF相交于点0,试探究∠BO与直线MN、EF所夹锐角的数量关系.
3、(4分)已知△ABC中,AB=AC,∠A=36°,仿照图①,请你再设计两种不同的分法,将△ABC分割成3个三角形,使得每个三角形都是等腰三角形.
4、(10分)如图,AB=A C, ∠BAC=120°,AD⊥AB,AE⊥A C.
(1)写出图中等于30°的角: .
等于60°的角有: .(2分)
(2)△ADE是等边三角形吗 为什么?(4分)
(3)在Rt△ABD中,∠B= °,AD= BD;在Rt△ACE中,有类似的结论吗
试用一句话概括你得出的结论。(4分)
5、(10分)如图,梯形ABCD中,AD∥BC,AB= DC =AD=3,BD⊥CD.
(1) 求∠DBC的度数 (2)求B C的长
6、(8分)如图,中,AB=AC,2条角平分线BD、CE相交于点O。
(1)OB与OC相等吗?请说明你的理由;
(2)若连接AO,并延长AO交BC边于F点。你有哪些发现?请写出两条,并就其中的一条发现写出你的发现过程。
7、(10分)如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
(1)图中有几个等腰三角形 猜想: EF与BE、CF之间有怎样的关系,并说明理由.
(2)如图②,若AB≠AC,其他条件不变,图中还有等腰三角形吗 如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗 EF与BE、CF关系又如何 说明你的理由。
2008年北京 2004年雅典 1988年汉城 1980年莫斯科
C
D
B
E
F
A
第6题图
第7题图
第2题图
第3题图
第6题图
E
B
P
F
C
A
第5题图
班级 姓名 评价
一.选择题:(请把你认为正确的答案前的字母填入下表内,每题3分,共24分)
题号 1 2 3 4 5 6 7 8
答案
⒈下列图案中是轴对称图形的是
A B C D
2、下列说法正确的是( ).
A.等腰梯形不是轴对称图形 B.等腰梯形相邻两内角都相等
C.等腰梯形两对角线相等 D.任一梯形都是轴对称图形
3.在△ABC中,①若AB=BC=CA,则△ABC为等边三角形;②若∠A=∠B=∠C,则△ABC为等边三角形;③有两个角都是60°的三角形是等边三角形;④一个角为60°的等腰三角形是等边三角形.上述结论中正确的有
A.1个 B.2个 C.3个 D.4个
4 如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,则下列四个结论,其中正确的个数是
①∠DEF=∠DFE ②AE=AF ③AD垂直平分EF ④EF垂直平分AD
A.1个 B.2个 C.3个 D.4个
5如图,已知△ABC中,AB
6、如图,△ABC中,AB=AC,∠ABC=36°,D,E为BC上的点,且∠BAD=∠DAE=∠EAC,则图中共有等腰三角形( )个.
A.2个 B.4个 C.6个 D.8个
7、如图,在等腰梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则图中全等三角形有( ). A.1对 B.2对 C.3对 D.4对
8. 如图甲,四边形ABCD是等腰梯形,AB∥DC.由4个这样的等腰梯形可以拼出图乙所示的平行四边形,则∠A的度数为( )A.50° B. 60° C. 70° D. 80°
二.填空题:(每题3分,共24分)
1等腰三角形的一个外角为110°,则它的另两个角是____ ____.
2、(1)如图,由Rt△CDE≌Rt△ACF,可得∠DCE+∠ACF= °,从而∠ACB= °.
(2)设小方格的边长为1,则AB= ;
(3)取AB的中点M,连接CM.则CM= ,理由是: .
3、如图,△ABC中,AB=AC,D是BC的中点,A C的垂直平分线EF分别交A C、AD、AB于点E、F、G.那么,点F到△ABC的边 的距离相等,点F到△ABC
的顶点 的距离相等.
4、代号为①、②、③、④的4张三角形纸片都有一个角为50°.如果它们另有一个角分别为50°、70°、80°、90°,那么其中只有代号为 的纸片能沿直线剪一刀得到等腰梯形.
5、如图,在梯形ABCD中,AD∥BC,DE∥AB,AD=4 cm,△DEC的周长为12 cm,则BE= ,梯形ABCD的周长= .
7、如图,已知中,,,直角的顶点是 中点,两边,分别交,于点,,给出以下四个结论:①,② ,③是等腰直角三角形,④。当在内绕顶点旋转时(点不与,重合),上述结论中始终正确的序号有 .
8.如图,∠AOB是一钢架,且∠AOB=10°,为了使钢架更加坚固,需在其内部添加一些钢管EF,FG,GH:……添加的钢管长度都与0E相等,则最多能添这样的钢管 根.
三.解答题:(本大题共8题,共52分)
1、(4分)利用图中的网格线,分别以线段MN和PQ为一底,画一个底角为45°的等腰梯形,且使它的另外2个顶点也在格点上.
2、(6分)如图,△ABC和△关于直线MN对称,△和△关于直线EF对称.
(1)画出直线EF;
(2)直线MN与EF相交于点0,试探究∠BO与直线MN、EF所夹锐角的数量关系.
3、(4分)已知△ABC中,AB=AC,∠A=36°,仿照图①,请你再设计两种不同的分法,将△ABC分割成3个三角形,使得每个三角形都是等腰三角形.
4、(10分)如图,AB=A C, ∠BAC=120°,AD⊥AB,AE⊥A C.
(1)写出图中等于30°的角: .
等于60°的角有: .(2分)
(2)△ADE是等边三角形吗 为什么?(4分)
(3)在Rt△ABD中,∠B= °,AD= BD;在Rt△ACE中,有类似的结论吗
试用一句话概括你得出的结论。(4分)
5、(10分)如图,梯形ABCD中,AD∥BC,AB= DC =AD=3,BD⊥CD.
(1) 求∠DBC的度数 (2)求B C的长
6、(8分)如图,中,AB=AC,2条角平分线BD、CE相交于点O。
(1)OB与OC相等吗?请说明你的理由;
(2)若连接AO,并延长AO交BC边于F点。你有哪些发现?请写出两条,并就其中的一条发现写出你的发现过程。
7、(10分)如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
(1)图中有几个等腰三角形 猜想: EF与BE、CF之间有怎样的关系,并说明理由.
(2)如图②,若AB≠AC,其他条件不变,图中还有等腰三角形吗 如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗 EF与BE、CF关系又如何 说明你的理由。
2008年北京 2004年雅典 1988年汉城 1980年莫斯科
C
D
B
E
F
A
第6题图
第7题图
第2题图
第3题图
第6题图
E
B
P
F
C
A
第5题图
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
