第二十四图形的相似判定复习(2)
图片预览



文档简介
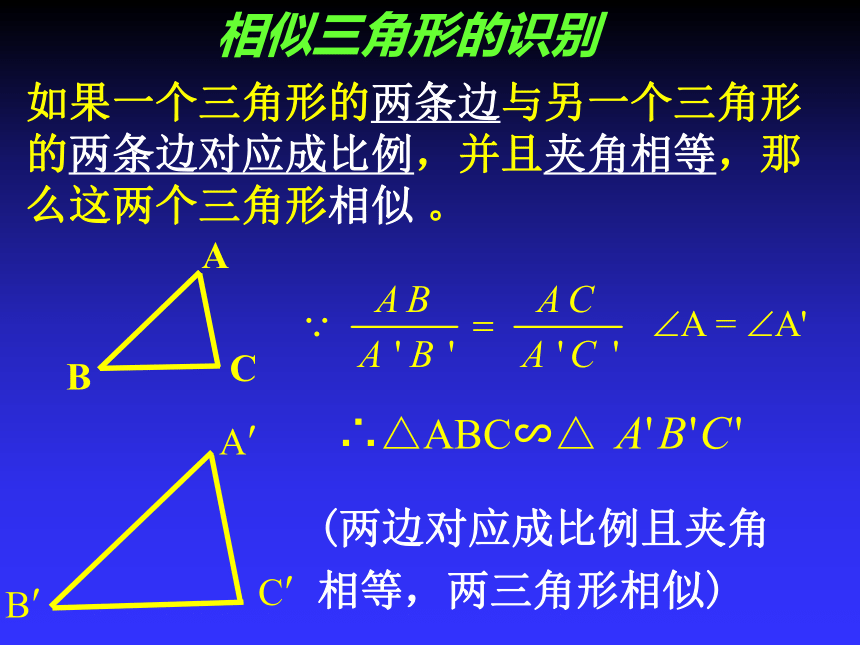
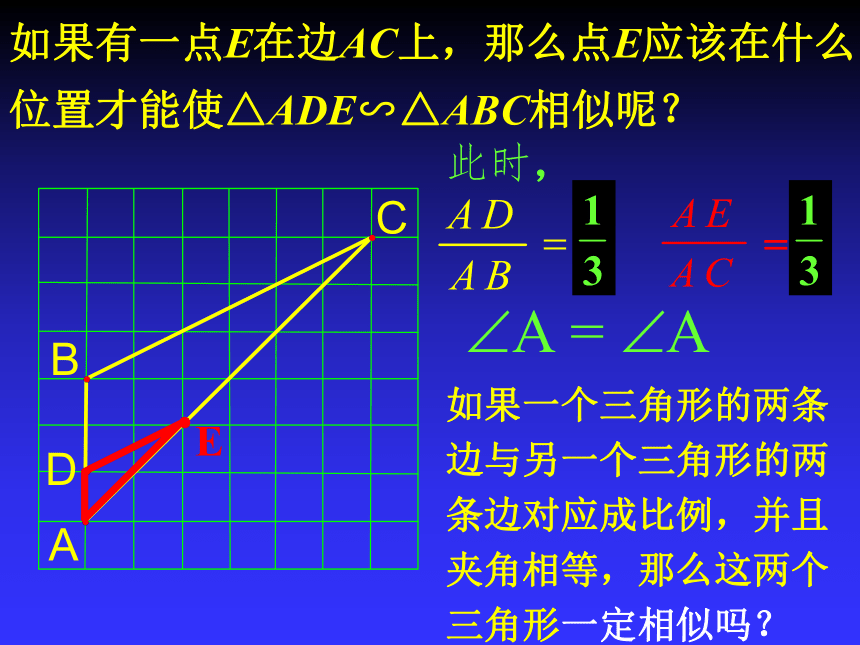
课件17张PPT。第24章.图形相似的判定复习(2)相似三角形的识别方法有那些?方法1:通过定义方法5:通过两角对应相等。课 堂 回顾方法2:平行于三角形一边的直线。方法3:三边对应成比例。方法4:两边对应成比例且夹角。相似三角形的识别 ∴△ABC∽△如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似 。(两边对应成比例且夹角相等,两三角形相似)A如果有一点E在边AC上,那么点E应该在什么位置才能使△ADE∽△ABC相似呢? 此时,如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形一定相似吗? =?已知:如图△ABC和△A`B`C`中,∠A=∠A` , ∠A` ,A`B`:AB=A`C`:AC.
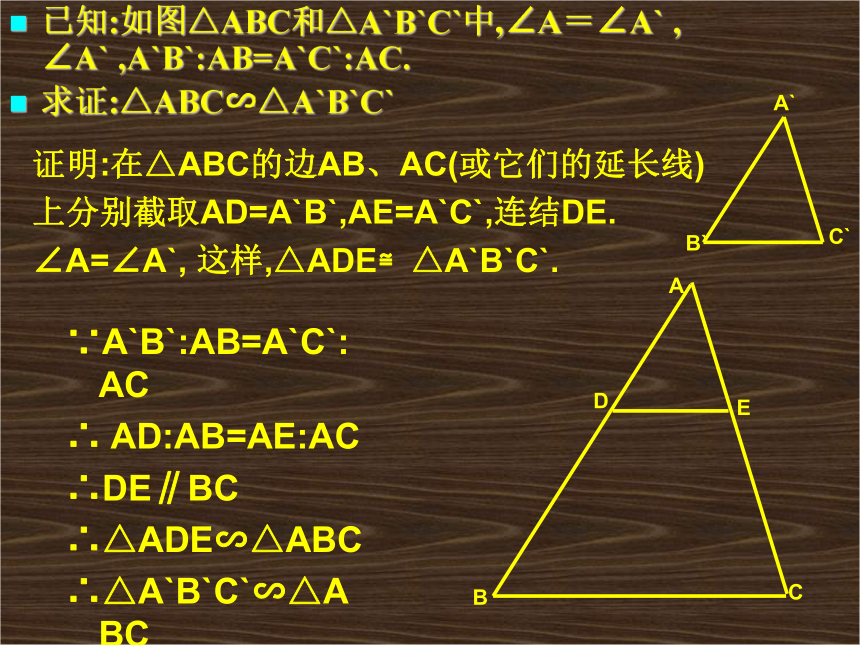
求证:△ABC∽△A`B`C`ABCED证明:在△ABC的边AB、AC(或它们的延长线)
上分别截取AD=A`B`,AE=A`C`,连结DE.
∠A=∠A`, 这样,△ADE≌△A`B`C`.∵A`B`:AB=A`C`:AC
∴ AD:AB=AE:AC
∴DE∥BC
∴△ADE∽△ABC
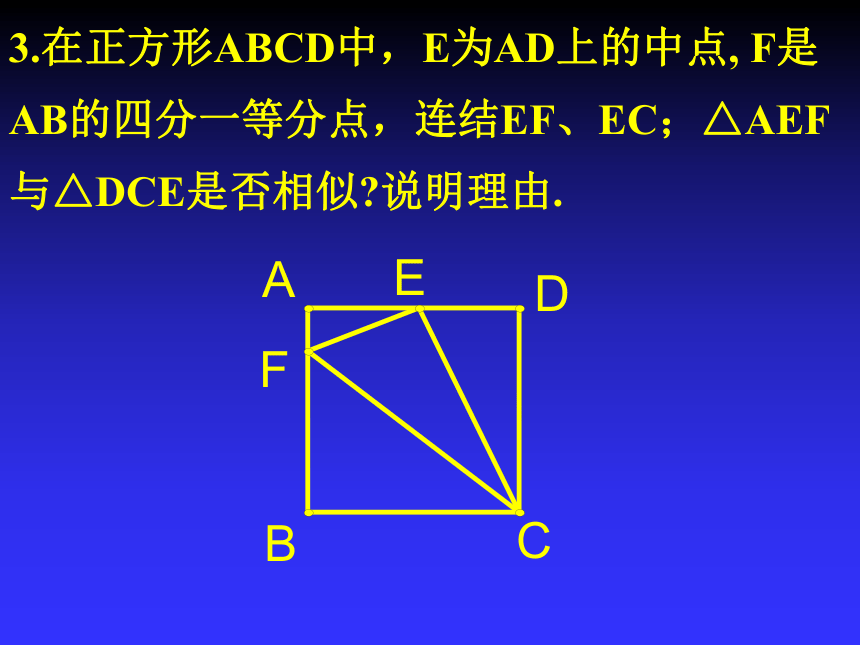
∴△A`B`C`∽△ABC ∵ = =1.52、判断图中△AEB和△FEC是否相似? 解:∴△AEB∽△FEC ∵∠1=∠2 = =1.5∴ =123.在正方形ABCD中,E为AD上的中点, F是AB的四分一等分点,连结EF、EC;△AEF与△DCE是否相似?说明理由.4、已知:如图,BD、CE是△ABC的高,
试说明 △ADE∽△ABC。例1 如图所示,在两个直角三角形△ABC和△A′B′C′中,∠B=∠B′=90°,∠A=∠A′,判断这两个三角形是否相似. 解:∵ ∠B=∠B′=90°(已知),∠A=∠A′(已知), ∴ △ABC∽△A′B′C′(两个角分别对应相等的两个三角形相似.) 例2. 如图,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC. 解: ∵ DE∥BC,EF∥AB(已知),∴ ∠ADE=∠B=∠EFC (两直线平行,同位角相等)∠AED=∠C. (两直线平行,同位角相等)∴ △ADE∽△EFC. (两个角分别对应相等的两个三角形相似.)找一找(1)图1中DE∥FG∥BC,找出图中所有的相似三角形。(2)图2中AB∥CD∥EF,找出图中所有的相似三角形。答:相似三角形有 △ADE∽△AFG∽△ABC。答:相似三角形有 △AOB∽△FOE∽△DOC。 (3)在△ABC和△A′B′C′中,如果∠A=80°,∠C=60°,∠A′=80°,∠B′=40°,那么这两个三角形是否相似?为什么?∠B=180 °-(∠A+∠C)=180 °-(80 °+60 °)=40 °填一填
(1)如图3,点D在AB上,当∠ =∠ 时,
△ACD∽△ABC。
(2)如图4,已知点E在AC上,若点D在AB上,则满足
条件 ,就可以使△ADE与原△ABC相似。
∠ ACD∠ B (或者∠ ACB=∠ ADB)DE//BCD(或者∠ C=∠ ADE)(或者∠ B=∠ ADE)DEABDC解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =43.已知如图, ∠ABD=∠C AD=2 AC=8,求AB DBCA18 5、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D ABDCEF问:若E是BC中点,ED的延长线交BA的延长线于F,
求证:AB : AC=DF : BF泰勒斯测量金字塔高度的示意图: 如果人体高度AC=1.7米,人影长BC=2.2米,而B′C′=176米,你能求出金字塔的高度并说明其中的道理吗?可证△ABC∽△A’B’C’
即
所以A’ C’=1.7x176÷2.2=136m? 平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似;? 三边对应成比例,两三角形相似.相似三角形的判定方法? 两边对应成比例且夹角相等,两三角形相似.
求证:△ABC∽△A`B`C`ABCED证明:在△ABC的边AB、AC(或它们的延长线)
上分别截取AD=A`B`,AE=A`C`,连结DE.
∠A=∠A`, 这样,△ADE≌△A`B`C`.∵A`B`:AB=A`C`:AC
∴ AD:AB=AE:AC
∴DE∥BC
∴△ADE∽△ABC
∴△A`B`C`∽△ABC ∵ = =1.52、判断图中△AEB和△FEC是否相似? 解:∴△AEB∽△FEC ∵∠1=∠2 = =1.5∴ =123.在正方形ABCD中,E为AD上的中点, F是AB的四分一等分点,连结EF、EC;△AEF与△DCE是否相似?说明理由.4、已知:如图,BD、CE是△ABC的高,
试说明 △ADE∽△ABC。例1 如图所示,在两个直角三角形△ABC和△A′B′C′中,∠B=∠B′=90°,∠A=∠A′,判断这两个三角形是否相似. 解:∵ ∠B=∠B′=90°(已知),∠A=∠A′(已知), ∴ △ABC∽△A′B′C′(两个角分别对应相等的两个三角形相似.) 例2. 如图,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC. 解: ∵ DE∥BC,EF∥AB(已知),∴ ∠ADE=∠B=∠EFC (两直线平行,同位角相等)∠AED=∠C. (两直线平行,同位角相等)∴ △ADE∽△EFC. (两个角分别对应相等的两个三角形相似.)找一找(1)图1中DE∥FG∥BC,找出图中所有的相似三角形。(2)图2中AB∥CD∥EF,找出图中所有的相似三角形。答:相似三角形有 △ADE∽△AFG∽△ABC。答:相似三角形有 △AOB∽△FOE∽△DOC。 (3)在△ABC和△A′B′C′中,如果∠A=80°,∠C=60°,∠A′=80°,∠B′=40°,那么这两个三角形是否相似?为什么?∠B=180 °-(∠A+∠C)=180 °-(80 °+60 °)=40 °填一填
(1)如图3,点D在AB上,当∠ =∠ 时,
△ACD∽△ABC。
(2)如图4,已知点E在AC上,若点D在AB上,则满足
条件 ,就可以使△ADE与原△ABC相似。
∠ ACD∠ B (或者∠ ACB=∠ ADB)DE//BCD(或者∠ C=∠ ADE)(或者∠ B=∠ ADE)DEABDC解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =43.已知如图, ∠ABD=∠C AD=2 AC=8,求AB DBCA18 5、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D ABDCEF问:若E是BC中点,ED的延长线交BA的延长线于F,
求证:AB : AC=DF : BF泰勒斯测量金字塔高度的示意图: 如果人体高度AC=1.7米,人影长BC=2.2米,而B′C′=176米,你能求出金字塔的高度并说明其中的道理吗?可证△ABC∽△A’B’C’
即
所以A’ C’=1.7x176÷2.2=136m? 平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似;? 三边对应成比例,两三角形相似.相似三角形的判定方法? 两边对应成比例且夹角相等,两三角形相似.
