四川省成都市石室阳安学校2023-2024学年高一上学期12月月考数学试题(无答案)
文档属性
| 名称 | 四川省成都市石室阳安学校2023-2024学年高一上学期12月月考数学试题(无答案) | 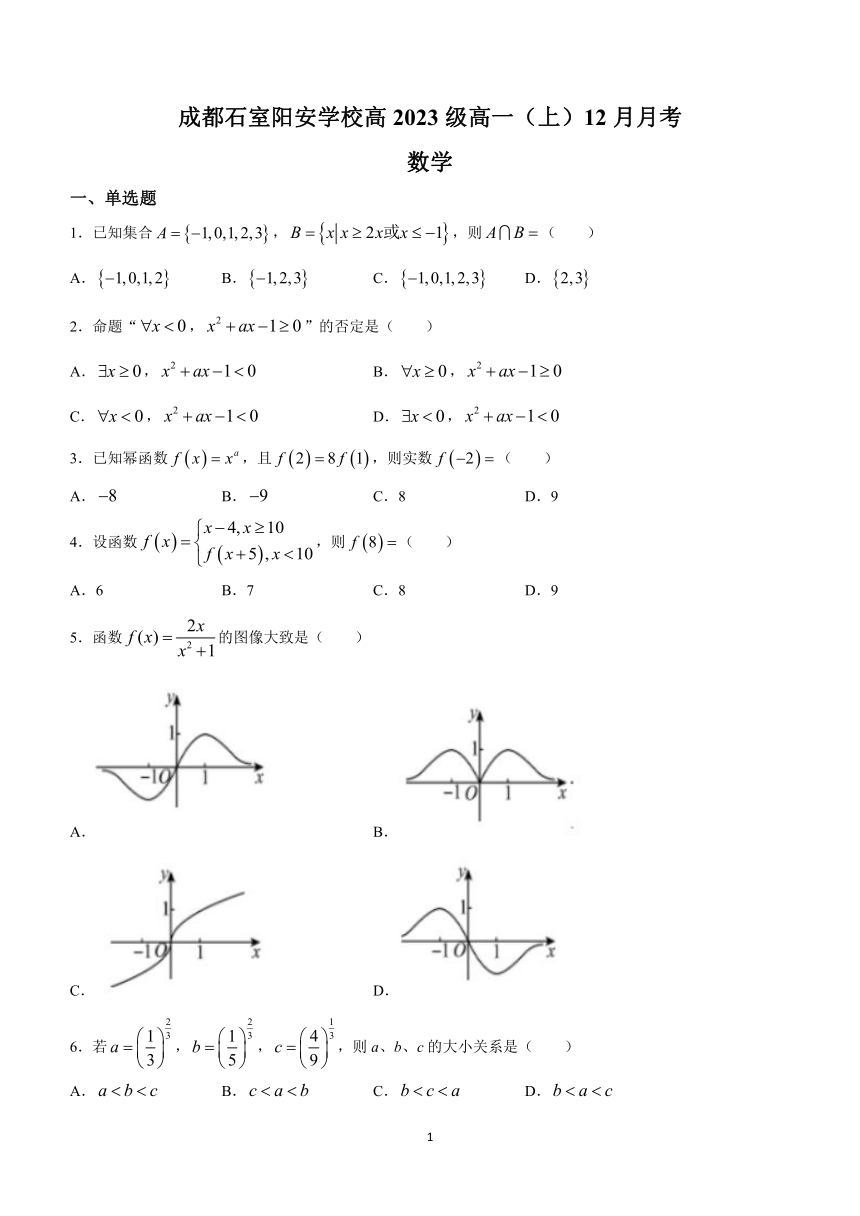 | |
| 格式 | doc | ||
| 文件大小 | 309.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-09 09:18:47 | ||
图片预览


文档简介
成都石室阳安学校高2023级高一(上)12月月考
数学
一、单选题
1.已知集合,,则( )
A. B. C. D.
2.命题“,”的否定是( )
A., B.,
C., D.,
3.已知幂函数,且,则实数( )
A. B. C.8 D.9
4.设函数,则( )
A.6 B.7 C.8 D.9
5.函数的图像大致是( )
A. B.
C. D.
6.若,,,则a、b、c的大小关系是( )
A. B. C. D.
7.若,则的值为( )
A.2 B.3 C.5 D.6
8.已知是定义在R上的奇函数,当时,,则不等式的解集为( )
A. B.
C. D.
二、多选题
9.若实数,则下列说法正确的是( )
A. B. C. D.
10.下列说法正确的是( )
A.“”是“”的充分不必要条件
B.函数与是同一函数
C.函数的单调递增区间是
D.已知的定义域为,则函数的定义域为
11.若函数在上是减函数,则关于实数a的可能取值是( )
A. B. C.0 D.1
12.已知函数的图象关于成中心对称图形的充要条件是是奇函数,函数的图象关于成轴对称图形的充要条件是是偶函数.则下列说法正确的是( )
A.的对称中心为 B.关于对称
C.的对称中心为 D.,的图象关于对称
三、填空题
13.已知函数,则______.
14.若a、b为正实数,且,则ab的最大值为______.
15.已知某种果蔬的有效保鲜时间y(单位:小时)与储藏温度x(单位:℃)近似满足函数关系(a,b为常数,e为自然对数底数),若该果蔬在4℃的保鲜时间为216小时,在16℃的有效保鲜时间为8小时,那么在8℃时,该果蔬的有效保鲜时间大约为_____小时.
16.已知定义域为R的函数,则满足条件的实数t的取值范围是______.
四、解答题
17.化简求值
(1) (2)
18.求下列函数的值域和单调区间.
(1),; (2),
19.求解下面两题:
(1)已知关于x的不等式的解集为,求不等的解集;
(2)若对于任意实数x,不等式恒成立,求实数k的取值范围.
20.己知函数(且)的图象过点.
(1)求a的值及的定义域;
(2)判断的奇偶性,并说明理由.
21.党的二十大报告明确要求继续深化国有企业改革,培育具有全球竞争力的世界一流企业.某企业抓住机遇推进生产改革,现在准备从单一产品转为生产A、B两种产品,根据市场调查与市场预测,生产A产品的利润与投资成正比,其关系如图①;生产B产品的利润与投资的算术平方根成正比,其关系如图②(注:所示图中的横坐标表示投资金额,单位为万元).
图① 图②
(1)分别求出生产A、B两种产品的利润表示为投资的函数关系式;
(2)该企业已筹集到12万元资金,并全部投入A、B两种产品的生产,问:怎样分配这12万元资金,才能使企业获得最大利润,最大利润是多少?
22.已知函数(且).
(1)当时,解不等式;
(2)若对于任意的,都有,求实数m的取值范围;
(3)在(2)的条件下,是否存在,使在区间上的值域是?若存在,求实数m的取值范围:若不存在,说明理由.
数学
一、单选题
1.已知集合,,则( )
A. B. C. D.
2.命题“,”的否定是( )
A., B.,
C., D.,
3.已知幂函数,且,则实数( )
A. B. C.8 D.9
4.设函数,则( )
A.6 B.7 C.8 D.9
5.函数的图像大致是( )
A. B.
C. D.
6.若,,,则a、b、c的大小关系是( )
A. B. C. D.
7.若,则的值为( )
A.2 B.3 C.5 D.6
8.已知是定义在R上的奇函数,当时,,则不等式的解集为( )
A. B.
C. D.
二、多选题
9.若实数,则下列说法正确的是( )
A. B. C. D.
10.下列说法正确的是( )
A.“”是“”的充分不必要条件
B.函数与是同一函数
C.函数的单调递增区间是
D.已知的定义域为,则函数的定义域为
11.若函数在上是减函数,则关于实数a的可能取值是( )
A. B. C.0 D.1
12.已知函数的图象关于成中心对称图形的充要条件是是奇函数,函数的图象关于成轴对称图形的充要条件是是偶函数.则下列说法正确的是( )
A.的对称中心为 B.关于对称
C.的对称中心为 D.,的图象关于对称
三、填空题
13.已知函数,则______.
14.若a、b为正实数,且,则ab的最大值为______.
15.已知某种果蔬的有效保鲜时间y(单位:小时)与储藏温度x(单位:℃)近似满足函数关系(a,b为常数,e为自然对数底数),若该果蔬在4℃的保鲜时间为216小时,在16℃的有效保鲜时间为8小时,那么在8℃时,该果蔬的有效保鲜时间大约为_____小时.
16.已知定义域为R的函数,则满足条件的实数t的取值范围是______.
四、解答题
17.化简求值
(1) (2)
18.求下列函数的值域和单调区间.
(1),; (2),
19.求解下面两题:
(1)已知关于x的不等式的解集为,求不等的解集;
(2)若对于任意实数x,不等式恒成立,求实数k的取值范围.
20.己知函数(且)的图象过点.
(1)求a的值及的定义域;
(2)判断的奇偶性,并说明理由.
21.党的二十大报告明确要求继续深化国有企业改革,培育具有全球竞争力的世界一流企业.某企业抓住机遇推进生产改革,现在准备从单一产品转为生产A、B两种产品,根据市场调查与市场预测,生产A产品的利润与投资成正比,其关系如图①;生产B产品的利润与投资的算术平方根成正比,其关系如图②(注:所示图中的横坐标表示投资金额,单位为万元).
图① 图②
(1)分别求出生产A、B两种产品的利润表示为投资的函数关系式;
(2)该企业已筹集到12万元资金,并全部投入A、B两种产品的生产,问:怎样分配这12万元资金,才能使企业获得最大利润,最大利润是多少?
22.已知函数(且).
(1)当时,解不等式;
(2)若对于任意的,都有,求实数m的取值范围;
(3)在(2)的条件下,是否存在,使在区间上的值域是?若存在,求实数m的取值范围:若不存在,说明理由.
同课章节目录
