12.1轴对称(2)
图片预览




文档简介
课件20张PPT。12.1.2轴对称的性质回顾与思考1、两个图形成轴对称与轴对称图形是否是同一回事?
它们有何区别与联系?答:“两个图形成轴对称”是指两个图形之间的形状与位置关系;“轴对称图形”是指一个图形的位置与形状关系。 一个图形可分割成两个图形,当这两个图形关于某直线对称时原来的那个轴对称图形就成为两个图形成轴对称;
反过来,如果把成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形。 2、一个轴对称图形的对称轴是否只有一条?答:不一定只有一条。
有的轴对称图形的对称轴不一定只有一条。
通常画出所有的对称轴,这样有利于多角度、
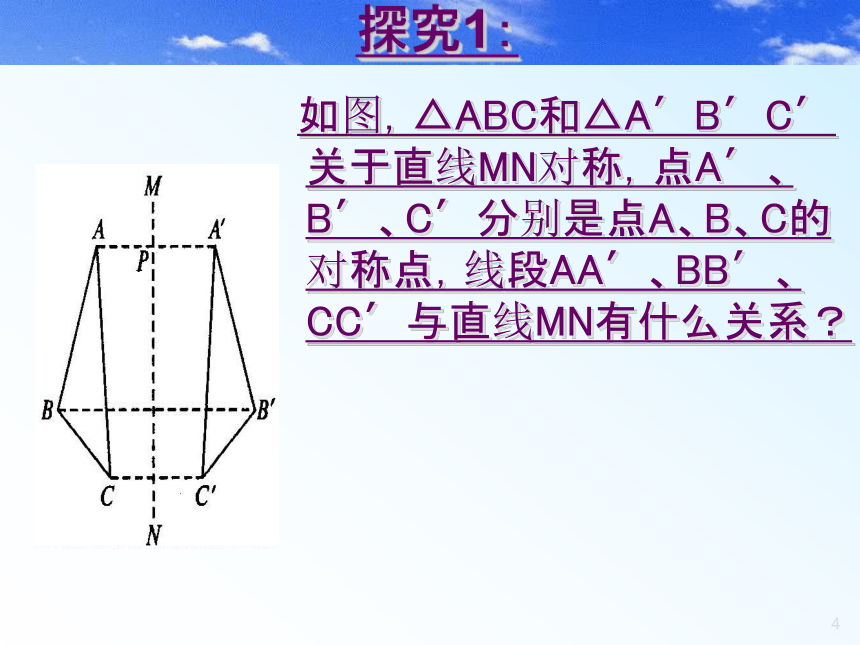
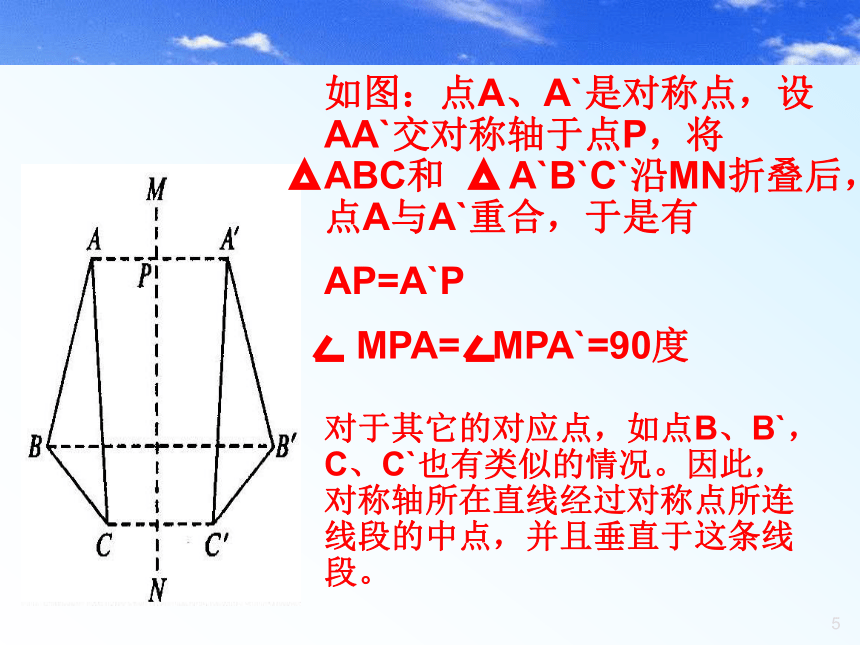
灵活地研究几何图形。 学 习 目 标 弄清几种简单的轴对称图形; 探究1: 如图,△ABC和△A′B′C′关于直线MN对称,点A′、B′、C′分别是点A、B、C的对称点,线段AA′、BB′、CC′与直线MN有什么关系?如图:点A、A`是对称点,设AA`交对称轴于点P,将 ABC和 A`B`C`沿MN折叠后,点A与A`重合,于是有
AP=A`P
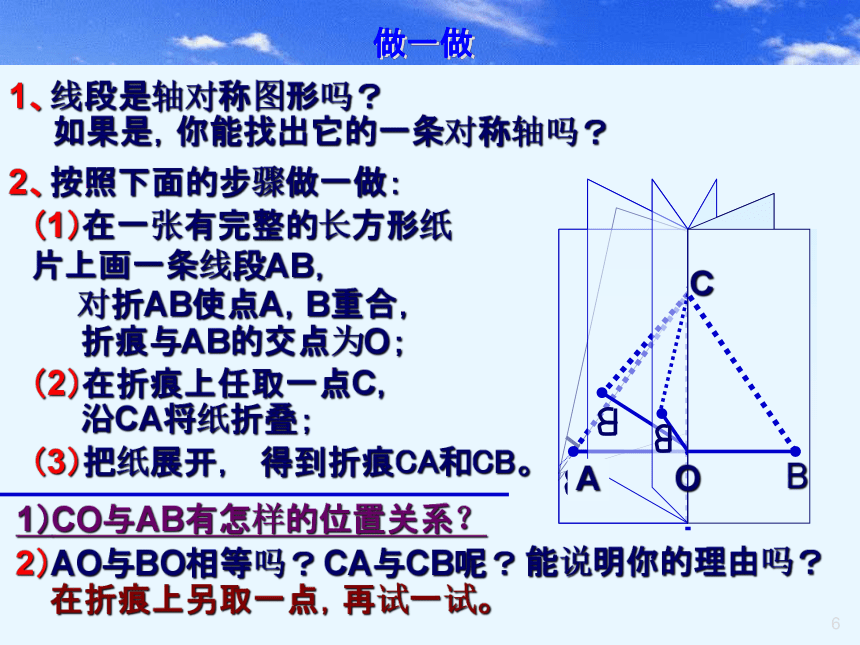
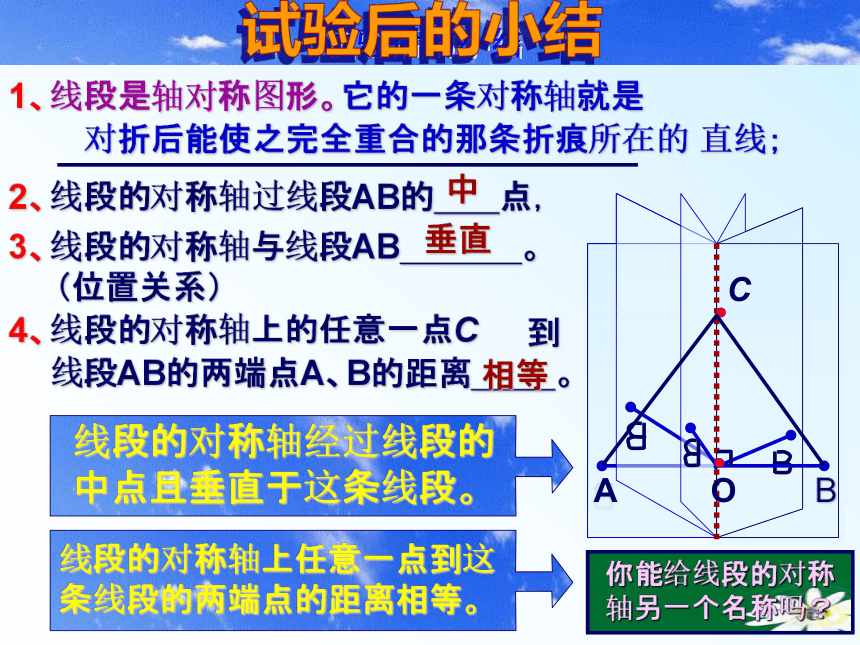
MPA= MPA`=90度对于其它的对应点,如点B、B`,C、C`也有类似的情况。因此,对称轴所在直线经过对称点所连线段的中点,并且垂直于这条线段。做一做1、线段是轴对称图形吗?如果是,你能找出它的一条对称轴吗?2、按照下面的步骤做一做:(1)在一张有完整的长方形纸片上画一条线段AB,对折AB使点A,B重合,折痕与AB的交点为O;O(2)在折痕上任取一点C,沿CA将纸折叠;(3)把纸展开,AO得到折痕CA和CB。2)AO与BO相等吗?CA与CB呢?能说明你的理由吗?在折痕上另取一点,再试一试。试验后的小结1、线段是轴对称图形。试验后的小结对折后能使之完全重合的那条折痕所在的 直线;2、线段的对称轴过线段AB的 点,中O3、线段的对称轴与线段AB 。
(位置关系)垂直4、线段的对称轴上的任意一点C 到
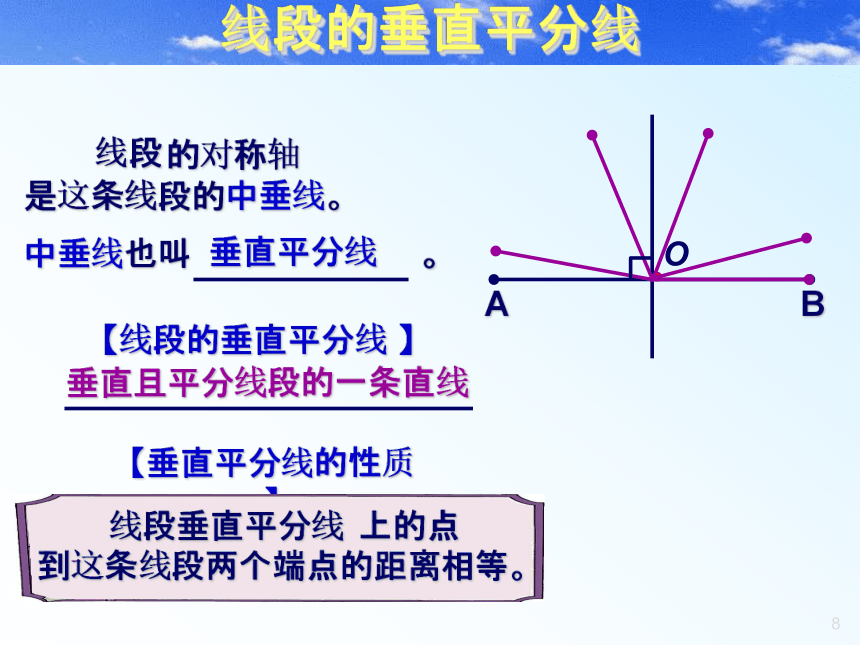
线段AB的两端点A、B的距离 。相等你能给线段的对称轴另一个名称吗?线段的对称轴是这条线段的中垂线。垂直平分线垂直且平分线段的一条直线线段的垂直平分线 上的点
到这条线段两个端点的距离相等。 归纳图形轴对称的性质: 如果两个图形关于某条直线对称,那么对称轴是任何一对对称点所连线段的垂直平分线.
类似地,轴对称图形的对称轴是任何一对对称点所连线段的垂直平分线.[探究2]如左图.木条L与AB钉在一起,L垂直平分AB,P1,P2,P3,…是L上的点,分别量一量点P1,P2,P3,…到A与B的距离,你有什么发现?
图2线段垂直平分线上的点到线段两端的距离相等。
[探究3]如图.用一根木棒和一根弹性均匀的橡皮筋,做一个简易的“弓”,“箭”通过木棒中央的孔射出去,怎么才能保持出箭的方向与木棒垂直呢?为什么? 与一条线段两端的距离相等的点在这条线段垂直平分线上。
结论:线段垂直平分线上的点到线段两端的距离相等。
反之,与一条线段两端的距离相等的点在这条线段垂直平分线上。
所以,线段垂直平分线可以看作到线段两
端的距离相等的所有点的集合。数学与生活:一条街道旁有两个小区,在街道什么位置建一个供水站,使它与两个小区的距离相等?请你帮助设计。 街道居民区B居民区A拓展:如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长。NMCBA随堂练习 :1.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC、CE的长度有什么关系?AB+BD与DE有什么关系?AOB角是轴对称图形吗?如果是,请找出它的
对称轴;角的对称轴是 角的平分线所在的直线。角平分线的性质CE=CD 角的平分线上的点到这个角的两边的距离相等。E感悟与反思小结角的平分线的性质—— 本节课你学到了什么?线段的对称轴是线段的垂直平分线(中垂线) ;角的对称轴是角的平分线所在的直线; 线段垂直平分线上的点
到这条线段两个端点的距离相等。 角的平分线上的点到这个角的两边的距离相等。拓展练习拓展练习 如图,在△ABC中,∠C等于900,AB的中垂线DE交BC于D,交AB于E,连接AD,若AD平分∠BAC,找出图中相等的线段,并说说你的理由。CBE你能找到图中特殊的三角形吗?你能找到图中相等的角吗?解:∵ AB的中垂线DE交BC于D,
交AB于E,∴ EB=EA ,DB=DA ;∵ AD平分∠BAC ,DC⊥AC、DE⊥AB,∴ DC=DE 。Rt△AcD、Rt△AED、Rt△ACB、Rt△BED、EDBCA解:∵DE是线段BC的垂直平分线 ,∴EC=EB∴△BCE 的周长
=EB+EC+BC
=6+6+10=22。 △ABC中,BC=10,边BC 的垂直平分线分别交AB、BC于点E、D,BE=6,求△BCE 的周长.拓展练习拓展练习6=6BE=6 某一个星期六,某中学初一年级的同学参加义务劳动,
其中有四个班的同学分别在M、N两处参加劳动,另外四个班的同学分别在道路AB、AC两处劳动,现要在道路AB、AC的交叉区域内设一个荼水供应点P ,使P到两条道路的距离相等,且使 PM= PN,请你找出点P的位置,并说明理由。 AMBNC拓展练习拓展练习P
它们有何区别与联系?答:“两个图形成轴对称”是指两个图形之间的形状与位置关系;“轴对称图形”是指一个图形的位置与形状关系。 一个图形可分割成两个图形,当这两个图形关于某直线对称时原来的那个轴对称图形就成为两个图形成轴对称;
反过来,如果把成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形。 2、一个轴对称图形的对称轴是否只有一条?答:不一定只有一条。
有的轴对称图形的对称轴不一定只有一条。
通常画出所有的对称轴,这样有利于多角度、
灵活地研究几何图形。 学 习 目 标 弄清几种简单的轴对称图形; 探究1: 如图,△ABC和△A′B′C′关于直线MN对称,点A′、B′、C′分别是点A、B、C的对称点,线段AA′、BB′、CC′与直线MN有什么关系?如图:点A、A`是对称点,设AA`交对称轴于点P,将 ABC和 A`B`C`沿MN折叠后,点A与A`重合,于是有
AP=A`P
MPA= MPA`=90度对于其它的对应点,如点B、B`,C、C`也有类似的情况。因此,对称轴所在直线经过对称点所连线段的中点,并且垂直于这条线段。做一做1、线段是轴对称图形吗?如果是,你能找出它的一条对称轴吗?2、按照下面的步骤做一做:(1)在一张有完整的长方形纸片上画一条线段AB,对折AB使点A,B重合,折痕与AB的交点为O;O(2)在折痕上任取一点C,沿CA将纸折叠;(3)把纸展开,AO得到折痕CA和CB。2)AO与BO相等吗?CA与CB呢?能说明你的理由吗?在折痕上另取一点,再试一试。试验后的小结1、线段是轴对称图形。试验后的小结对折后能使之完全重合的那条折痕所在的 直线;2、线段的对称轴过线段AB的 点,中O3、线段的对称轴与线段AB 。
(位置关系)垂直4、线段的对称轴上的任意一点C 到
线段AB的两端点A、B的距离 。相等你能给线段的对称轴另一个名称吗?线段的对称轴是这条线段的中垂线。垂直平分线垂直且平分线段的一条直线线段的垂直平分线 上的点
到这条线段两个端点的距离相等。 归纳图形轴对称的性质: 如果两个图形关于某条直线对称,那么对称轴是任何一对对称点所连线段的垂直平分线.
类似地,轴对称图形的对称轴是任何一对对称点所连线段的垂直平分线.[探究2]如左图.木条L与AB钉在一起,L垂直平分AB,P1,P2,P3,…是L上的点,分别量一量点P1,P2,P3,…到A与B的距离,你有什么发现?
图2线段垂直平分线上的点到线段两端的距离相等。
[探究3]如图.用一根木棒和一根弹性均匀的橡皮筋,做一个简易的“弓”,“箭”通过木棒中央的孔射出去,怎么才能保持出箭的方向与木棒垂直呢?为什么? 与一条线段两端的距离相等的点在这条线段垂直平分线上。
结论:线段垂直平分线上的点到线段两端的距离相等。
反之,与一条线段两端的距离相等的点在这条线段垂直平分线上。
所以,线段垂直平分线可以看作到线段两
端的距离相等的所有点的集合。数学与生活:一条街道旁有两个小区,在街道什么位置建一个供水站,使它与两个小区的距离相等?请你帮助设计。 街道居民区B居民区A拓展:如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长。NMCBA随堂练习 :1.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC、CE的长度有什么关系?AB+BD与DE有什么关系?AOB角是轴对称图形吗?如果是,请找出它的
对称轴;角的对称轴是 角的平分线所在的直线。角平分线的性质CE=CD 角的平分线上的点到这个角的两边的距离相等。E感悟与反思小结角的平分线的性质—— 本节课你学到了什么?线段的对称轴是线段的垂直平分线(中垂线) ;角的对称轴是角的平分线所在的直线; 线段垂直平分线上的点
到这条线段两个端点的距离相等。 角的平分线上的点到这个角的两边的距离相等。拓展练习拓展练习 如图,在△ABC中,∠C等于900,AB的中垂线DE交BC于D,交AB于E,连接AD,若AD平分∠BAC,找出图中相等的线段,并说说你的理由。CBE你能找到图中特殊的三角形吗?你能找到图中相等的角吗?解:∵ AB的中垂线DE交BC于D,
交AB于E,∴ EB=EA ,DB=DA ;∵ AD平分∠BAC ,DC⊥AC、DE⊥AB,∴ DC=DE 。Rt△AcD、Rt△AED、Rt△ACB、Rt△BED、EDBCA解:∵DE是线段BC的垂直平分线 ,∴EC=EB∴△BCE 的周长
=EB+EC+BC
=6+6+10=22。 △ABC中,BC=10,边BC 的垂直平分线分别交AB、BC于点E、D,BE=6,求△BCE 的周长.拓展练习拓展练习6=6BE=6 某一个星期六,某中学初一年级的同学参加义务劳动,
其中有四个班的同学分别在M、N两处参加劳动,另外四个班的同学分别在道路AB、AC两处劳动,现要在道路AB、AC的交叉区域内设一个荼水供应点P ,使P到两条道路的距离相等,且使 PM= PN,请你找出点P的位置,并说明理由。 AMBNC拓展练习拓展练习P
