圆解决问题特训卷(思维拓展篇)数学六年级上册人教版(含解析)
文档属性
| 名称 | 圆解决问题特训卷(思维拓展篇)数学六年级上册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 15:18:48 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
圆解决问题特训卷(思维拓展篇)数学六年级上册人教版
1.将一个周长56.52cm的圆形纸片的半径缩短2cm,它的面积将减少多少平方厘米?
2.一个圆形水池的直径是16米,现在要在它的周围加宽2米,加宽后水池的面积比原来增加了多少平方米?
3.坐落于贵州省平塘县克度镇的中国“天眼”是世界上口径最大的单天线射电望远镜,它的口径(即外口直径)是500米,它的占地面积是多少平方米?合多少公顷?
4.一个半圆形的羊圈,半径是5米。
(1)修这个羊圈需要多长的栅栏?
(2)如果要扩建这个羊圈,把它的直径增加2米.羊圈的面积增加了多少?
5.刘爷爷整理了一块直径是6m的圆形菜地。
(1)如果在菜地内按2∶3种上西红柿和茄子,种西红柿的面积是多少平方米?
(2)刘爷爷要在菜地周围铺上一条1m宽的沙石路,这条沙石路的面积是多少平方米?
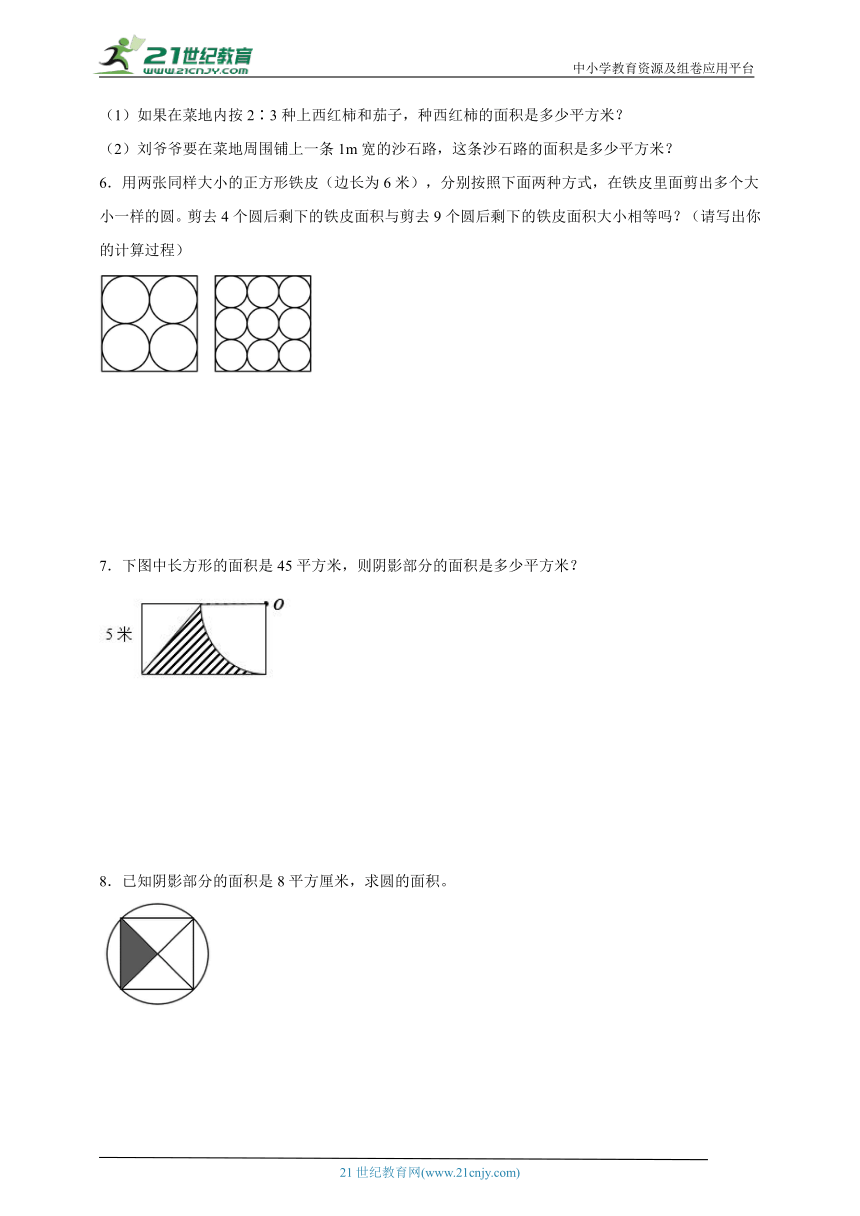
6.用两张同样大小的正方形铁皮(边长为6米),分别按照下面两种方式,在铁皮里面剪出多个大小一样的圆。剪去4个圆后剩下的铁皮面积与剪去9个圆后剩下的铁皮面积大小相等吗?(请写出你的计算过程)
7.下图中长方形的面积是45平方米,则阴影部分的面积是多少平方米?
8.已知阴影部分的面积是8平方厘米,求圆的面积。
9.公园里有一段宽2米的步行小道(如图),如果铺设这条小道每平方米的造价是150元,铺设这条小道需要投入资金多少元?
10.把一个圆转化成近似的长方形,已知长方形的周长比圆的周长多4厘米.
(1)请试着把这个圆画出来.
(2)请计算出这个圆的面积.
11.用6米长的绳子把一只羊拴在了一块长20米、宽15米的长方形草地中央的木桩上。请问:这只羊能吃到全部的青草吗?请说明理由。(提示:可以先画出示意图进行分析)
12.图中阴影部分甲的面积比乙多57平方厘米,直径AB的长为20cm,求CB的长。
13.如图,李大伯在一个上底14m、下底28m的梯形地里刚好挖了一个与梯形的四条边都相接的最大的圆形池塘,剩余部分作为草坪,池塘的半径为10m,草坪的面积是多少平方米?
14.根据相关研究。室外景点人均活动面积低于0.75平方米时。就有发生踩踏事故的危险。在一个古镇景点戏台前,有一片半径是20米的半圆形室外场地,为保证安全,这片场上最多只能容纳多少人同时看戏?
15.将一个直径为16m的圆形菜园进行扩建,扩建后的直径与原来直径的比是3:1,扩建后圆形菜园的面积是多少平方米
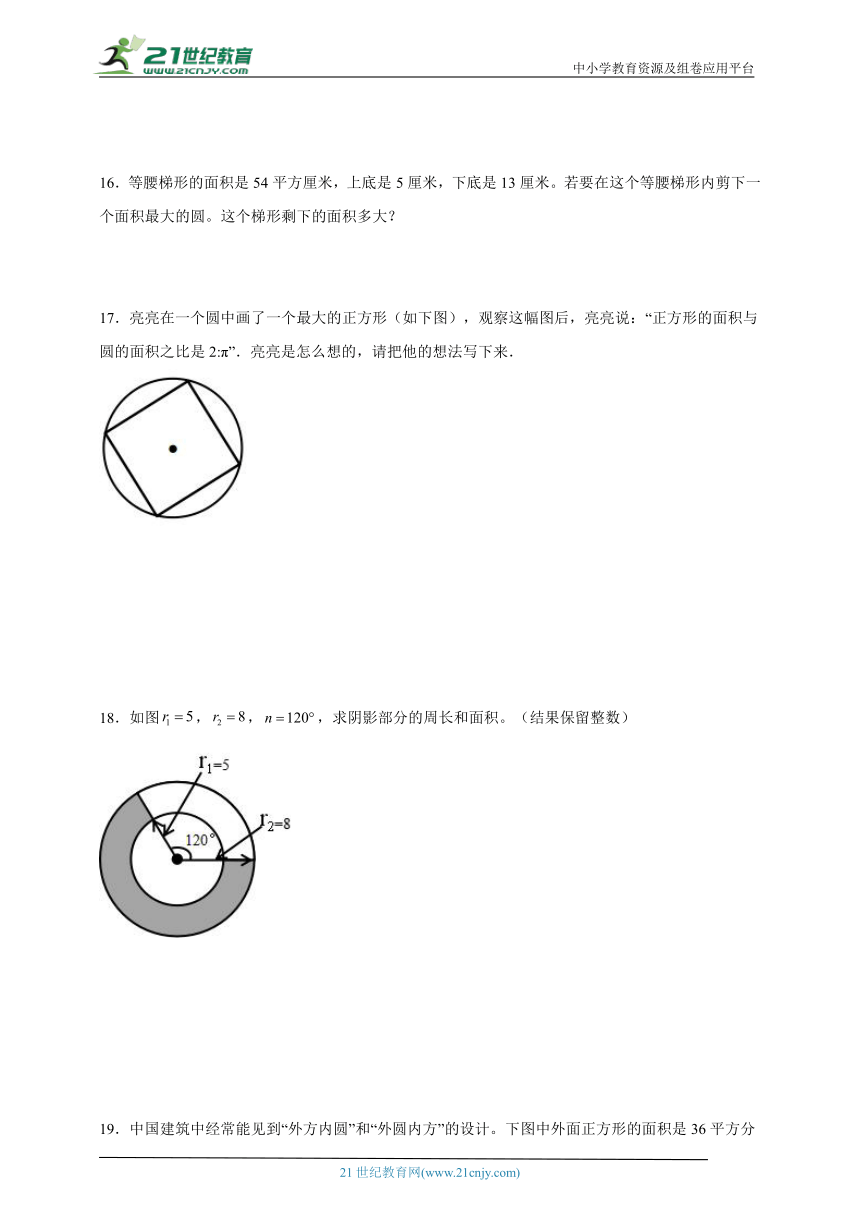
16.等腰梯形的面积是54平方厘米,上底是5厘米,下底是13厘米。若要在这个等腰梯形内剪下一个面积最大的圆。这个梯形剩下的面积多大?
17.亮亮在一个圆中画了一个最大的正方形(如下图),观察这幅图后,亮亮说:“正方形的面积与圆的面积之比是2:π”.亮亮是怎么想的,请把他的想法写下来.
18.如图,,,求阴影部分的周长和面积。(结果保留整数)
19.中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。下图中外面正方形的面积是36平方分米,你能求出正方形和圆之间部分的面积吗?
20.如图所示,正方形的边长为8cm,求阴影部分的面积。
21.在广场的一角有一个如图的花坛,花坛外又铺了2米宽的草坪,如果铺每平方米草坪要100元,铺这块草坪需要多少元?
参考答案:
1.100.48平方厘米
【详解】56.52÷3.14÷2=9(厘米)
9-2=7(厘米)
3.14×9×9=254.34(平方厘米)
254.34-3.14×7×7=100.48(平方厘米)
2.113.04平方米
【分析】加宽后水池的面积比原来增加的面积可看作是环形部分面积,则先确定环形部分的内圈半径,再确定外圈半径,并依据公式S环=πR2-πr2来计算。
【详解】16÷2=8(米)
3.14×[(8+2) -8 ]
=3.14×[100-64]
=3.14×36
=113.04(平方米)
答:加宽后水池的面积比原来增加了113.04平方米。
【点睛】题目共有三句话,第一句提供了内圈直径的长度;第二句要经过转化,可变成外圈半径长度;最后一句话是问题的提出。
3.196250平方米,19.625公顷
【分析】根据圆的面积=πr ,列式解答即可,根据1公顷=10000平方米,进行换算。
【详解】3.14×(500÷2)2
=3.14×62500
=196250(m2)
=19.625(公顷)
答:它的占地面积是196250平方米,合19.625公顷。
【点睛】关键是掌握圆的面积公式,单位小变大除以进率。
4.(1)25.7米 (2)17.27平方米
【分析】(1)直接计算半径是5米圆周长的一半,再加一个直径长度即可;
(2)利用扩建后羊圈的面积(半径5+2÷2=6米半圆的面积)减去原来羊圈的面积(半径为5米半圆的面积)即可。
【详解】(1)3.14×5×2÷2+5×2
=15.7+10
=25.7(米)
答:修这个羊圈需要25.7米长的栅栏。
(2)[3.14×(5+2÷2)2-3.14×52]÷2
=[3.14×36-3.14×25]÷2
=[113.04-78.5]÷2
=34.54÷2
=17.27(平方米)
答:羊圈的面积增加了17.27平方米。
【点睛】此题考查利用圆的周长和面积计算公式来解决实际问题。
5.(1)11.304平方米;
(2)21.98平方米
【分析】(1)根据直径计算出圆形菜地的半径,再利用求出这块圆形菜地的面积,最后根据比的应用求出种西红柿的面积;
(2)大圆半径=小圆半径+环宽,利用求出这条沙石路的面积,据此解答。
【详解】(1)圆形菜地的面积:3.14×(6÷2)2
=3.14×9
=28.26(平方米)
种西红柿的面积:28.26×=11.304(平方米)
答:种西红柿的面积是11.304平方米。
(2)3.14×[(6÷2+1)2-(6÷2)2]
=3.14×[42-32]
=3.14×7
=21.98(平方米)
答:这条沙石路的面积是21.98平方米。
【点睛】掌握圆和环形的面积计算公式是解答题目的关键。
6.相等
【分析】由题意可知:左图剩下的铁皮的面积=正方形的面积―4个小圆的面积;右图剩下的铁皮的面积=正方形的面积―9个小圆的面积。根据正方形的面积=边长×边长,圆的面积=πr2,代入数据计算即可。
【详解】正方形的面积:(平方米)
(米)
(米)
(平方米)
所以左图剩下的铁皮的面积是:(平方米)
(米)
(米)
(平方米)
所以右图剩下的铁皮的面积是:(平方米)
答:剪去4个圆后剩下的铁皮面积与剪去9个圆后剩下的铁皮面积大小相等。
【点睛】考查求正方形的面积以及圆的面积,牢记公式是关键。
7.15.375平方米
【分析】长方形的面积是45平方米,宽是5米,那么长为(45÷5)米,因此阴影部分的面积等于右边梯形的面积减去个圆的面积即可。
【详解】(45÷5+5)×5÷2-×3.14×52
=(9+5)×5÷2-×3.14×25
=14×5÷2-19.625
=35-19.625
=15.375(平方米)
答:阴影部分的面积是15.375平方米。
【点睛】此题解答的关键在于看出阴影部分是由哪几个图形面积的和或差得出。
8.50.24平方厘米
【分析】阴影部分是以圆的半径r为直角边的小三角形,根据三角形的面积公式可得:这个三角形的面积是r2÷2=8平方厘米,所以可得:r2=8×2,将其代入圆的面积公式中即可求得该圆的面积。
【详解】阴影部分三角形的面积是:r2÷2=8(平方厘米),所以可得:r2=8×2;
8×2×3.14
=16×3.14
=50.24(平方厘米)
答:这个圆的面积是50.24平方厘米。
【点睛】根据图中小直角三角形的面积,得出:=8×2,是解决本题的关键。
9.11304元
【分析】铺设小道的面积等于直径是14米的圆的面积减去直径是10米的圆的面积,再求出投入资金即可。
【详解】10÷2=5(米)
5+2=7(米)
3.14×(72-52)×150
=3.14×24×150
=75.36×150
=11304(元)
答:铺设这条小道需要投入资金11304元。
【点睛】本题考查圆的面积,解答本题的关键是掌握圆的面积计算公式。
10.如图,面积是12.56平方厘米
【分析】由圆的面积公式的推导过程可知,长方形的周长比圆的周长多2个圆的半径,由“长方形的周长比圆的周长多4厘米”即可求出圆的半径;以任意一点为圆心,以求出的半径为半径即可画出需要的圆,进而依据圆的面积公式即可求解.
【详解】4÷2=2(厘米),
以O为圆心,以2厘米为半径画圆(如下图);
3.14×22=12.56(平方厘米);
答:这个圆的面积是12.56平方厘米.
11.这只羊不能吃到全部的青草,具体见详解。
【分析】先画示意图,以木桩所在的地方为圆心,6米为圆心画圆,看圆是否覆盖整个长方形草地即可。也可以根据圆的面积公式求出羊所能吃到的面积,与长方形的面积比较即可。
【详解】如图所示,O点为木桩所在点,则羊的活动范围是以O为圆心,6米为半径的圆,即图中的蓝色区域。因为O点是草地的中央,那么OA的距离=15÷2=7.5(米),而6米<7.5米,所以羊不能吃到全部的青草。
或者:圆的面积=3.14×6×6=113.04(平方米),长方形的面积=20×15=300(平方米),113.04<300,所以这只羊不能吃到全部的青草。
答:这只羊不能吃到全部的青草。
【点睛】熟练掌握圆的面积公式与长方形的面积是解题的关键。
12.10厘米
【分析】根据图可知空白处是半圆和三角形的公有部分,阴影部分甲的面积比阴乙的面积多57平方厘米,也就是说半圆比三角形ABC的面积大57平方厘米,又因为已知直径,可求出半圆的面积,用半圆面积减去57平方厘米就是三角形的面积,最后根据三角形的面积公式可以求出BC的长。
【详解】由题意可知:
半圆面积=π×()2÷2,
=3.14×102÷2,
=3.14×100÷2,
=157(平方厘米);
所以:SABC=157﹣57=100(平方厘米),
SABC=BC×AB÷2,
100=BC×20÷2,
BC=10(厘米);
答:BC的长为10厘米。
【点睛】此题考查了组合图形的面积中,转化思想的灵活应用。
13.106平方米
【分析】看图,用池塘的半径乘2,可求出梯形地的高。根据梯形和圆的面积公式,分别求出地的面积、池塘的面积,最后用地的面积减去池塘的面积,求出草坪的面积。
【详解】10×2=20(米)
(14+28)×20÷2
=42×10
=420(平方米)
3.14×102=314(平方米)
420-314=106(平方米)
答:草坪的面积是106平方米。
【点睛】本题考查了梯形和圆的面积,掌握二者的面积公式是解题的关键。
14.1674人
【分析】根据圆的面积公式:S=πr2,据此求出半圆形室外场地的面积,然后再除以0.75即可求解。
【详解】3.14×202÷0.75
=1256÷0.75
≈1674(人)
答:为保证安全,这片场上最多只能容纳1674人同时看戏。
【点睛】本题考查圆的面积,熟记公式是解题的关键。
15.1808.64㎡
【详解】扩建后的直径为:16×3=48(m)
扩建后的面积是:3.14×(48÷2=1808.64(㎡)
16.25.74平方厘米
【分析】等腰梯形的高是54×2÷(5+13)=6厘米,那么面积最大的圆可能是直径为6厘米的圆,再检查这个圆和两个腰,发现是分离的,说明梯形内最大的圆应该是直径为6厘米(半径为3厘米)的圆,则梯形剩下的面积是54-9×3.14平方厘米。
【详解】等腰梯形的高是:
54×2÷(5+13)
=54×2÷18
=108÷18
=6(厘米)
54-3.14×(6÷2)2
=54-3.14×9
=54-28.26
=25.74(平方厘米)
答:梯形剩下的面积是25.74平方厘米。
17.解:设圆的半径是r,正方形面积:2r×r=2r2
圆的面积:πr2
2r2:πr2=2:π
【解析】略
18.周长:60;面积:81.64
【分析】根据图示,阴影部分的周长等于半径是8和5,圆心角是(360-120)°的弧长,加上两条8-5=3的线段;面积等于圆心角是360-120=240°的环形面积。利用圆环的面积公式:,圆的周长公式:,计算即可。
【详解】(3.14×5×2+3.14×8×2)×+(8-5)×2
=81.64×+6
≈54+6
=60
3.14×(82-52)×
=3.14×39×
=81.64
答:阴影部分的周长是60,面积为81.64。
【点睛】本题主要考查组合图形的周长面积,关键把组合图形转化为规则图形,利用规则图形的周长与面积公式计算。
19.7.74平方分米
【分析】已知正方形的面积是36平方分米,根据正方形的面积=边长×边长,可得正方形的边长为6分米,观察发现正方形的边长相当于是圆的直径,则圆的半径是(6÷2)分米,根据圆的面积公式,用3.14×(6÷2)2即可求出圆的面积,再求出正方形和圆面积的差即可。
【详解】6×6=36(平方分米)
圆的直径是6分米,
r:6÷2=3(分米)
3.14×3×3
=3.14×9
=28.26(平方分米)
36-28.26=7.74(平方分米)
答:正方形和圆之间部分的面积7.74平方分米。
【点睛】本题考查了正方形面积和圆面积公式的灵活应用,关键是明确正方形和圆之间的关系。
20.32
【详解】阴影部分面积占正方形面积的一半。
8×8÷2=32()
答:阴影部分的面积是32。
21.3140元
【分析】观察图形,草坪的面积是圆环的面积,大圆的半径是(9+2)米,小圆的半径是9米,根据圆环的面积公式,求出草坪的面积,然后再乘上100即可。
【详解】×3.14×[(9+2)2-92]×100
=×3.14×[112-81]×100
=×3.14×[121-81]×100
=×3.14×40×100
=31.4×100
=3140(元)
答:铺这块草坪需要3140元。
【点睛】本题关键是根据圆环的面积公式,求出草坪的面积,然后再根据乘法的意义进行解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
圆解决问题特训卷(思维拓展篇)数学六年级上册人教版
1.将一个周长56.52cm的圆形纸片的半径缩短2cm,它的面积将减少多少平方厘米?
2.一个圆形水池的直径是16米,现在要在它的周围加宽2米,加宽后水池的面积比原来增加了多少平方米?
3.坐落于贵州省平塘县克度镇的中国“天眼”是世界上口径最大的单天线射电望远镜,它的口径(即外口直径)是500米,它的占地面积是多少平方米?合多少公顷?
4.一个半圆形的羊圈,半径是5米。
(1)修这个羊圈需要多长的栅栏?
(2)如果要扩建这个羊圈,把它的直径增加2米.羊圈的面积增加了多少?
5.刘爷爷整理了一块直径是6m的圆形菜地。
(1)如果在菜地内按2∶3种上西红柿和茄子,种西红柿的面积是多少平方米?
(2)刘爷爷要在菜地周围铺上一条1m宽的沙石路,这条沙石路的面积是多少平方米?
6.用两张同样大小的正方形铁皮(边长为6米),分别按照下面两种方式,在铁皮里面剪出多个大小一样的圆。剪去4个圆后剩下的铁皮面积与剪去9个圆后剩下的铁皮面积大小相等吗?(请写出你的计算过程)
7.下图中长方形的面积是45平方米,则阴影部分的面积是多少平方米?
8.已知阴影部分的面积是8平方厘米,求圆的面积。
9.公园里有一段宽2米的步行小道(如图),如果铺设这条小道每平方米的造价是150元,铺设这条小道需要投入资金多少元?
10.把一个圆转化成近似的长方形,已知长方形的周长比圆的周长多4厘米.
(1)请试着把这个圆画出来.
(2)请计算出这个圆的面积.
11.用6米长的绳子把一只羊拴在了一块长20米、宽15米的长方形草地中央的木桩上。请问:这只羊能吃到全部的青草吗?请说明理由。(提示:可以先画出示意图进行分析)
12.图中阴影部分甲的面积比乙多57平方厘米,直径AB的长为20cm,求CB的长。
13.如图,李大伯在一个上底14m、下底28m的梯形地里刚好挖了一个与梯形的四条边都相接的最大的圆形池塘,剩余部分作为草坪,池塘的半径为10m,草坪的面积是多少平方米?
14.根据相关研究。室外景点人均活动面积低于0.75平方米时。就有发生踩踏事故的危险。在一个古镇景点戏台前,有一片半径是20米的半圆形室外场地,为保证安全,这片场上最多只能容纳多少人同时看戏?
15.将一个直径为16m的圆形菜园进行扩建,扩建后的直径与原来直径的比是3:1,扩建后圆形菜园的面积是多少平方米
16.等腰梯形的面积是54平方厘米,上底是5厘米,下底是13厘米。若要在这个等腰梯形内剪下一个面积最大的圆。这个梯形剩下的面积多大?
17.亮亮在一个圆中画了一个最大的正方形(如下图),观察这幅图后,亮亮说:“正方形的面积与圆的面积之比是2:π”.亮亮是怎么想的,请把他的想法写下来.
18.如图,,,求阴影部分的周长和面积。(结果保留整数)
19.中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。下图中外面正方形的面积是36平方分米,你能求出正方形和圆之间部分的面积吗?
20.如图所示,正方形的边长为8cm,求阴影部分的面积。
21.在广场的一角有一个如图的花坛,花坛外又铺了2米宽的草坪,如果铺每平方米草坪要100元,铺这块草坪需要多少元?
参考答案:
1.100.48平方厘米
【详解】56.52÷3.14÷2=9(厘米)
9-2=7(厘米)
3.14×9×9=254.34(平方厘米)
254.34-3.14×7×7=100.48(平方厘米)
2.113.04平方米
【分析】加宽后水池的面积比原来增加的面积可看作是环形部分面积,则先确定环形部分的内圈半径,再确定外圈半径,并依据公式S环=πR2-πr2来计算。
【详解】16÷2=8(米)
3.14×[(8+2) -8 ]
=3.14×[100-64]
=3.14×36
=113.04(平方米)
答:加宽后水池的面积比原来增加了113.04平方米。
【点睛】题目共有三句话,第一句提供了内圈直径的长度;第二句要经过转化,可变成外圈半径长度;最后一句话是问题的提出。
3.196250平方米,19.625公顷
【分析】根据圆的面积=πr ,列式解答即可,根据1公顷=10000平方米,进行换算。
【详解】3.14×(500÷2)2
=3.14×62500
=196250(m2)
=19.625(公顷)
答:它的占地面积是196250平方米,合19.625公顷。
【点睛】关键是掌握圆的面积公式,单位小变大除以进率。
4.(1)25.7米 (2)17.27平方米
【分析】(1)直接计算半径是5米圆周长的一半,再加一个直径长度即可;
(2)利用扩建后羊圈的面积(半径5+2÷2=6米半圆的面积)减去原来羊圈的面积(半径为5米半圆的面积)即可。
【详解】(1)3.14×5×2÷2+5×2
=15.7+10
=25.7(米)
答:修这个羊圈需要25.7米长的栅栏。
(2)[3.14×(5+2÷2)2-3.14×52]÷2
=[3.14×36-3.14×25]÷2
=[113.04-78.5]÷2
=34.54÷2
=17.27(平方米)
答:羊圈的面积增加了17.27平方米。
【点睛】此题考查利用圆的周长和面积计算公式来解决实际问题。
5.(1)11.304平方米;
(2)21.98平方米
【分析】(1)根据直径计算出圆形菜地的半径,再利用求出这块圆形菜地的面积,最后根据比的应用求出种西红柿的面积;
(2)大圆半径=小圆半径+环宽,利用求出这条沙石路的面积,据此解答。
【详解】(1)圆形菜地的面积:3.14×(6÷2)2
=3.14×9
=28.26(平方米)
种西红柿的面积:28.26×=11.304(平方米)
答:种西红柿的面积是11.304平方米。
(2)3.14×[(6÷2+1)2-(6÷2)2]
=3.14×[42-32]
=3.14×7
=21.98(平方米)
答:这条沙石路的面积是21.98平方米。
【点睛】掌握圆和环形的面积计算公式是解答题目的关键。
6.相等
【分析】由题意可知:左图剩下的铁皮的面积=正方形的面积―4个小圆的面积;右图剩下的铁皮的面积=正方形的面积―9个小圆的面积。根据正方形的面积=边长×边长,圆的面积=πr2,代入数据计算即可。
【详解】正方形的面积:(平方米)
(米)
(米)
(平方米)
所以左图剩下的铁皮的面积是:(平方米)
(米)
(米)
(平方米)
所以右图剩下的铁皮的面积是:(平方米)
答:剪去4个圆后剩下的铁皮面积与剪去9个圆后剩下的铁皮面积大小相等。
【点睛】考查求正方形的面积以及圆的面积,牢记公式是关键。
7.15.375平方米
【分析】长方形的面积是45平方米,宽是5米,那么长为(45÷5)米,因此阴影部分的面积等于右边梯形的面积减去个圆的面积即可。
【详解】(45÷5+5)×5÷2-×3.14×52
=(9+5)×5÷2-×3.14×25
=14×5÷2-19.625
=35-19.625
=15.375(平方米)
答:阴影部分的面积是15.375平方米。
【点睛】此题解答的关键在于看出阴影部分是由哪几个图形面积的和或差得出。
8.50.24平方厘米
【分析】阴影部分是以圆的半径r为直角边的小三角形,根据三角形的面积公式可得:这个三角形的面积是r2÷2=8平方厘米,所以可得:r2=8×2,将其代入圆的面积公式中即可求得该圆的面积。
【详解】阴影部分三角形的面积是:r2÷2=8(平方厘米),所以可得:r2=8×2;
8×2×3.14
=16×3.14
=50.24(平方厘米)
答:这个圆的面积是50.24平方厘米。
【点睛】根据图中小直角三角形的面积,得出:=8×2,是解决本题的关键。
9.11304元
【分析】铺设小道的面积等于直径是14米的圆的面积减去直径是10米的圆的面积,再求出投入资金即可。
【详解】10÷2=5(米)
5+2=7(米)
3.14×(72-52)×150
=3.14×24×150
=75.36×150
=11304(元)
答:铺设这条小道需要投入资金11304元。
【点睛】本题考查圆的面积,解答本题的关键是掌握圆的面积计算公式。
10.如图,面积是12.56平方厘米
【分析】由圆的面积公式的推导过程可知,长方形的周长比圆的周长多2个圆的半径,由“长方形的周长比圆的周长多4厘米”即可求出圆的半径;以任意一点为圆心,以求出的半径为半径即可画出需要的圆,进而依据圆的面积公式即可求解.
【详解】4÷2=2(厘米),
以O为圆心,以2厘米为半径画圆(如下图);
3.14×22=12.56(平方厘米);
答:这个圆的面积是12.56平方厘米.
11.这只羊不能吃到全部的青草,具体见详解。
【分析】先画示意图,以木桩所在的地方为圆心,6米为圆心画圆,看圆是否覆盖整个长方形草地即可。也可以根据圆的面积公式求出羊所能吃到的面积,与长方形的面积比较即可。
【详解】如图所示,O点为木桩所在点,则羊的活动范围是以O为圆心,6米为半径的圆,即图中的蓝色区域。因为O点是草地的中央,那么OA的距离=15÷2=7.5(米),而6米<7.5米,所以羊不能吃到全部的青草。
或者:圆的面积=3.14×6×6=113.04(平方米),长方形的面积=20×15=300(平方米),113.04<300,所以这只羊不能吃到全部的青草。
答:这只羊不能吃到全部的青草。
【点睛】熟练掌握圆的面积公式与长方形的面积是解题的关键。
12.10厘米
【分析】根据图可知空白处是半圆和三角形的公有部分,阴影部分甲的面积比阴乙的面积多57平方厘米,也就是说半圆比三角形ABC的面积大57平方厘米,又因为已知直径,可求出半圆的面积,用半圆面积减去57平方厘米就是三角形的面积,最后根据三角形的面积公式可以求出BC的长。
【详解】由题意可知:
半圆面积=π×()2÷2,
=3.14×102÷2,
=3.14×100÷2,
=157(平方厘米);
所以:SABC=157﹣57=100(平方厘米),
SABC=BC×AB÷2,
100=BC×20÷2,
BC=10(厘米);
答:BC的长为10厘米。
【点睛】此题考查了组合图形的面积中,转化思想的灵活应用。
13.106平方米
【分析】看图,用池塘的半径乘2,可求出梯形地的高。根据梯形和圆的面积公式,分别求出地的面积、池塘的面积,最后用地的面积减去池塘的面积,求出草坪的面积。
【详解】10×2=20(米)
(14+28)×20÷2
=42×10
=420(平方米)
3.14×102=314(平方米)
420-314=106(平方米)
答:草坪的面积是106平方米。
【点睛】本题考查了梯形和圆的面积,掌握二者的面积公式是解题的关键。
14.1674人
【分析】根据圆的面积公式:S=πr2,据此求出半圆形室外场地的面积,然后再除以0.75即可求解。
【详解】3.14×202÷0.75
=1256÷0.75
≈1674(人)
答:为保证安全,这片场上最多只能容纳1674人同时看戏。
【点睛】本题考查圆的面积,熟记公式是解题的关键。
15.1808.64㎡
【详解】扩建后的直径为:16×3=48(m)
扩建后的面积是:3.14×(48÷2=1808.64(㎡)
16.25.74平方厘米
【分析】等腰梯形的高是54×2÷(5+13)=6厘米,那么面积最大的圆可能是直径为6厘米的圆,再检查这个圆和两个腰,发现是分离的,说明梯形内最大的圆应该是直径为6厘米(半径为3厘米)的圆,则梯形剩下的面积是54-9×3.14平方厘米。
【详解】等腰梯形的高是:
54×2÷(5+13)
=54×2÷18
=108÷18
=6(厘米)
54-3.14×(6÷2)2
=54-3.14×9
=54-28.26
=25.74(平方厘米)
答:梯形剩下的面积是25.74平方厘米。
17.解:设圆的半径是r,正方形面积:2r×r=2r2
圆的面积:πr2
2r2:πr2=2:π
【解析】略
18.周长:60;面积:81.64
【分析】根据图示,阴影部分的周长等于半径是8和5,圆心角是(360-120)°的弧长,加上两条8-5=3的线段;面积等于圆心角是360-120=240°的环形面积。利用圆环的面积公式:,圆的周长公式:,计算即可。
【详解】(3.14×5×2+3.14×8×2)×+(8-5)×2
=81.64×+6
≈54+6
=60
3.14×(82-52)×
=3.14×39×
=81.64
答:阴影部分的周长是60,面积为81.64。
【点睛】本题主要考查组合图形的周长面积,关键把组合图形转化为规则图形,利用规则图形的周长与面积公式计算。
19.7.74平方分米
【分析】已知正方形的面积是36平方分米,根据正方形的面积=边长×边长,可得正方形的边长为6分米,观察发现正方形的边长相当于是圆的直径,则圆的半径是(6÷2)分米,根据圆的面积公式,用3.14×(6÷2)2即可求出圆的面积,再求出正方形和圆面积的差即可。
【详解】6×6=36(平方分米)
圆的直径是6分米,
r:6÷2=3(分米)
3.14×3×3
=3.14×9
=28.26(平方分米)
36-28.26=7.74(平方分米)
答:正方形和圆之间部分的面积7.74平方分米。
【点睛】本题考查了正方形面积和圆面积公式的灵活应用,关键是明确正方形和圆之间的关系。
20.32
【详解】阴影部分面积占正方形面积的一半。
8×8÷2=32()
答:阴影部分的面积是32。
21.3140元
【分析】观察图形,草坪的面积是圆环的面积,大圆的半径是(9+2)米,小圆的半径是9米,根据圆环的面积公式,求出草坪的面积,然后再乘上100即可。
【详解】×3.14×[(9+2)2-92]×100
=×3.14×[112-81]×100
=×3.14×[121-81]×100
=×3.14×40×100
=31.4×100
=3140(元)
答:铺这块草坪需要3140元。
【点睛】本题关键是根据圆环的面积公式,求出草坪的面积,然后再根据乘法的意义进行解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
