2.1.1指数与指数幂的运算
图片预览











文档简介
课件38张PPT。 2.1指数函数
—2.1.1指数与指数幂的运算第一课时2008年9月22日第二章 基本初等函数(I)本节的学习内容:
根式、分数指数幂的概念以及利用分数指数的运算性质进行指数的运算.
学习本节的目的要求:
理解根式、分数指数的概念,掌握根式、分数指数的运算性质.
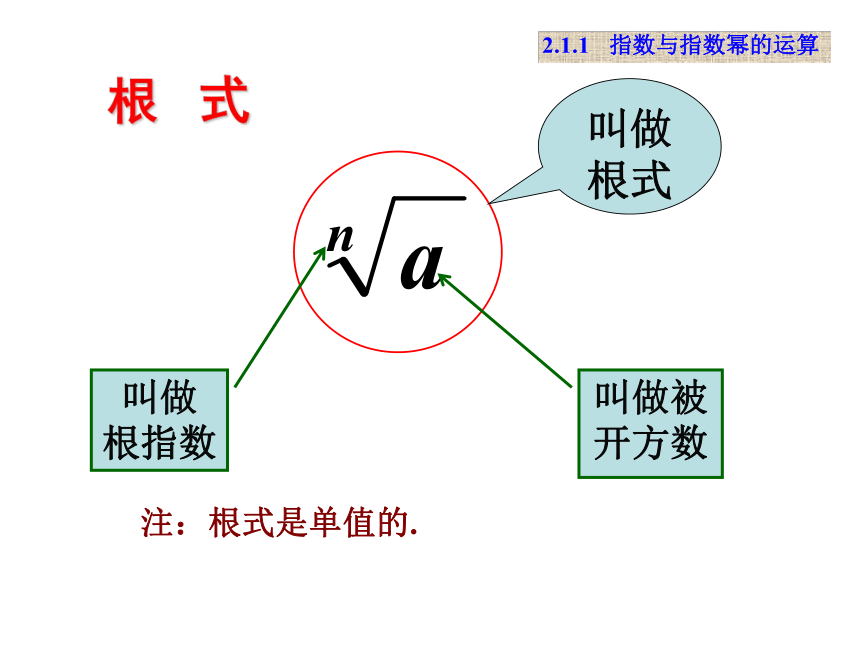
重点:分数指数幂的概念和分数指数的运算性质; 难点:根式的概念和分数指数幂的概念. 问题1:据国务院发展研究中心2000年发表的?未来20年我国发展前景分析?判断,未来20年,我GDP(国内生产总值)年平均增长率可望达到 ,那么,在2001~2020年,各年的GDP可望为2000年的多少倍?问题2:根 式1.n次方根的定义:根 式叫做根式叫做被开方数叫做
根指数根 式注:根式是单值的.2.根式的简单性质:根 式能力训练能力训练1.n次方根的定义:2.根式的简单性质:偶次方根有以下性质:正数的偶次方根有两个且是相反数;
负数没有偶次方根;
零的偶次方根是零。在实数范围内,正数的奇次方根是正数;
负数的奇次方根是负数;
零的奇次方根是零。奇次方根有以下性质:在实数范围内, 2.1指数函数
—2.1.1指数与指数幂的运算第二课时2008年9月23日第二章 基本初等函数(I)1.n次方根的定义:2.根式的简单性质:在初中学习了整数指数幂,即整数指数幂有哪些运算性质呢?分数指数幂1.当根式的被开方数的指数能被根指数整除时,根式可以写成分数指数幂的形式.2.当根式的被开方数的指数不能被根指数整除时,根式也可以写成分数指数幂的形式.重要结论:1)规定正数的正分数指数幂的意义: 正数的负分数指数幂的意义与负整数指数幂的意义相仿.2)规定:0正分数指数幂等于0,0的负分数指数幂没有意义.3)规定了分数指数的意义后,指数的概念就从整数指数推广到有理数指数.分数指数幂分数指数幂有理指数幂的运算性质能
力
训
练能力训练能力训练小结1.要使 有意义,则x的取值范围是2.计算:3.求值:备用 2.1指数函数
—2.1.1指数与指数幂的运算第三课时2008年9月24日第二章 基本初等函数(I)1. 分数指数幂的意义2.有理指数幂的运算性质值得注意的问题:快速练习CB 指数式的计算与化简,除了掌握定义、法则外,还要掌握一些变形技巧.根据题目的不同结构特征,灵活运用不同的技巧,才能做到运算合理准确快捷.一、巧用乘法公式 由于引入负指数及分数指数幂后,初中的平方差、立方差、完全平方公式等,有了新特征: 指数式的计算与化简能力训练二、巧用倒数三、化底为幂,化小数指数为分数把底数化为幂的形式.能力训练能力训练注:先化简再求值.能力训练讨论: 的结果? 讨论: 的结果? 讨论: 的结果? 小结小结1、本节的化简、求值问题,要注意整体代换,注意平方差、立方差、立方和等公式的运用。
2、将指数合理拆分,进而因式分解是指数运算中的常用技巧。
3、单项式乘以单项式、多项式乘以多项式
以及多项式除以单项式、多项式除以多项式的运算都没有改变。例1、计算下列各式(式中字母都是正数)例2、计算下列各式备用例3.化简:例4.备用例5.备用例6.备用
—2.1.1指数与指数幂的运算第一课时2008年9月22日第二章 基本初等函数(I)本节的学习内容:
根式、分数指数幂的概念以及利用分数指数的运算性质进行指数的运算.
学习本节的目的要求:
理解根式、分数指数的概念,掌握根式、分数指数的运算性质.
重点:分数指数幂的概念和分数指数的运算性质; 难点:根式的概念和分数指数幂的概念. 问题1:据国务院发展研究中心2000年发表的?未来20年我国发展前景分析?判断,未来20年,我GDP(国内生产总值)年平均增长率可望达到 ,那么,在2001~2020年,各年的GDP可望为2000年的多少倍?问题2:根 式1.n次方根的定义:根 式叫做根式叫做被开方数叫做
根指数根 式注:根式是单值的.2.根式的简单性质:根 式能力训练能力训练1.n次方根的定义:2.根式的简单性质:偶次方根有以下性质:正数的偶次方根有两个且是相反数;
负数没有偶次方根;
零的偶次方根是零。在实数范围内,正数的奇次方根是正数;
负数的奇次方根是负数;
零的奇次方根是零。奇次方根有以下性质:在实数范围内, 2.1指数函数
—2.1.1指数与指数幂的运算第二课时2008年9月23日第二章 基本初等函数(I)1.n次方根的定义:2.根式的简单性质:在初中学习了整数指数幂,即整数指数幂有哪些运算性质呢?分数指数幂1.当根式的被开方数的指数能被根指数整除时,根式可以写成分数指数幂的形式.2.当根式的被开方数的指数不能被根指数整除时,根式也可以写成分数指数幂的形式.重要结论:1)规定正数的正分数指数幂的意义: 正数的负分数指数幂的意义与负整数指数幂的意义相仿.2)规定:0正分数指数幂等于0,0的负分数指数幂没有意义.3)规定了分数指数的意义后,指数的概念就从整数指数推广到有理数指数.分数指数幂分数指数幂有理指数幂的运算性质能
力
训
练能力训练能力训练小结1.要使 有意义,则x的取值范围是2.计算:3.求值:备用 2.1指数函数
—2.1.1指数与指数幂的运算第三课时2008年9月24日第二章 基本初等函数(I)1. 分数指数幂的意义2.有理指数幂的运算性质值得注意的问题:快速练习CB 指数式的计算与化简,除了掌握定义、法则外,还要掌握一些变形技巧.根据题目的不同结构特征,灵活运用不同的技巧,才能做到运算合理准确快捷.一、巧用乘法公式 由于引入负指数及分数指数幂后,初中的平方差、立方差、完全平方公式等,有了新特征: 指数式的计算与化简能力训练二、巧用倒数三、化底为幂,化小数指数为分数把底数化为幂的形式.能力训练能力训练注:先化简再求值.能力训练讨论: 的结果? 讨论: 的结果? 讨论: 的结果? 小结小结1、本节的化简、求值问题,要注意整体代换,注意平方差、立方差、立方和等公式的运用。
2、将指数合理拆分,进而因式分解是指数运算中的常用技巧。
3、单项式乘以单项式、多项式乘以多项式
以及多项式除以单项式、多项式除以多项式的运算都没有改变。例1、计算下列各式(式中字母都是正数)例2、计算下列各式备用例3.化简:例4.备用例5.备用例6.备用
