5.5.2简单的三角恒等变换(一)学案
文档属性
| 名称 | 5.5.2简单的三角恒等变换(一)学案 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-09 16:26:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
5.5.2简单的三角恒等变换(一)
班级 姓名
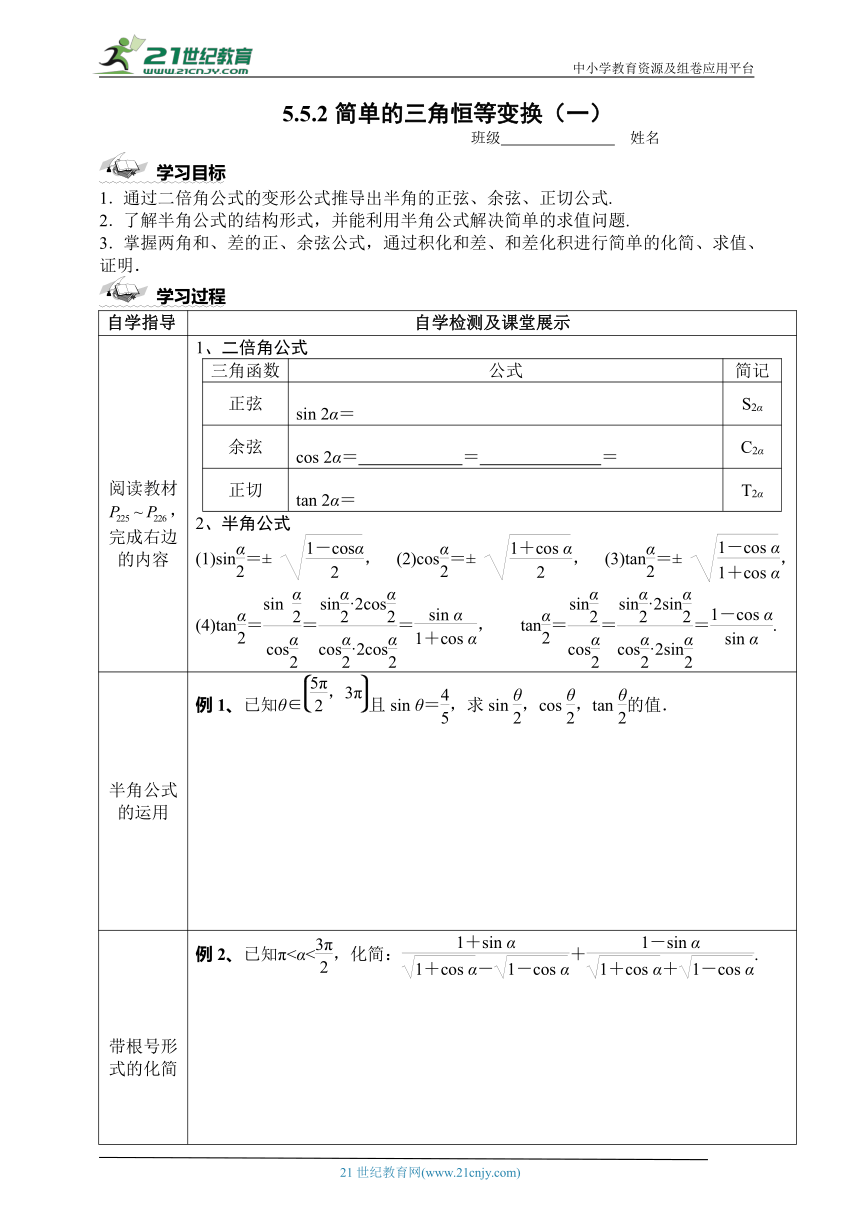
学习目标
1.通过二倍角公式的变形公式推导出半角的正弦、余弦、正切公式.
2.了解半角公式的结构形式,并能利用半角公式解决简单的求值问题.
3.掌握两角和、差的正、余弦公式,通过积化和差、和差化积进行简单的化简、求值、证明.
学习过程
自学指导 自学检测及课堂展示
阅读教材,完成右边的内容 1、二倍角公式三角函数公式简记正弦sin 2α= S2α余弦cos 2α= = = C2α正切tan 2α= T2α2、半角公式(1)sin=± , (2)cos=± , (3)tan=± ,(4)tan===, tan===.
半角公式的运用 例1、已知θ∈且sin θ=,求sin ,cos ,tan 的值.
带根号形式的化简 例2、已知π<α<,化简:+.变式1、化简:(1)+=________.(2)=________.
和差化积与积化和差 例3、证明:(1)sin αcos β=[sin(α+β)+sin(α-β)]; (2)sin θ+sin φ=2sin cos ; INCLUDEPICTURE "D:\\源文件\\2021\\同步\\数学\\人教A版必修第一册\\左括.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\苏德亭2021\\同步\\数学\\数学 人教A版 必修第一册\\新建文件夹\\左括.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\苏德亭2021\\同步\\数学\\数学 人教A版 必修第一册\\新建文件夹\\左括.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\苏德亭2021\\同步\\数学\\数学 人教A版 必修第一册\\新建文件夹\\左括.TIF" \* MERGEFORMATINET INCLUDEPICTURE "\\\\苏德亭\\d\\苏德亭2021\\同步\\数学\\数学 人教A版 必修第一册\\新建文件夹\\左括.TIF" \* MERGEFORMATINET 知识梳理 INCLUDEPICTURE "D:\\源文件\\2021\\同步\\数学\\人教A版必修第一册\\右括.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\苏德亭2021\\同步\\数学\\数学 人教A版 必修第一册\\新建文件夹\\右括.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\苏德亭2021\\同步\\数学\\数学 人教A版 必修第一册\\新建文件夹\\右括.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\苏德亭2021\\同步\\数学\\数学 人教A版 必修第一册\\新建文件夹\\右括.TIF" \* MERGEFORMATINET INCLUDEPICTURE "\\\\苏德亭\\d\\苏德亭2021\\同步\\数学\\数学 人教A版 必修第一册\\新建文件夹\\右括.TIF" \* MERGEFORMATINET 1.积化和差sin αcos β=[sin(α+β)+sin(α-β)]; cos αsin β=[sin(α+β)-sin(α-β)];cos αcos β=[cos(α+β)+cos(α-β)]; sin αsin β=-[cos(α+β)-cos(α-β)].2.和差化积sin θ+sin φ=2sin cos ; sin θ-sin φ=2cos sin ;cos θ+cos φ=2cos cos ; cos θ-cos φ=-2sin sin .
三角恒等式的证明 例4、求证:=sin 2α.
课后作业
一、基础训练题
1.已知cos α=-,<α<π,则sin 等于( )
A.- B.
C.- D.
2.已知sin α=,cos α=,则tan 等于( )
A.2- B.2+
C.-2 D.±(-2)
3.设-3π<α<-,化简的结果是( )
A.sin +cos B.-cos -sin
C.cos -sin D.sin -cos
4.化简的结果是( )
A.-cos 1 B.cos 1
C.cos 1 D.-cos 1
5.设a=cos 6°-sin 6°,b=2sin 13°cos 13°,c=,则有( )
A.cC.a6.sincos化为和差的结果是________.
7.= .
8.已知α∈,β∈,cos β=-,sin(α+β)=,则tan= ,sin α= .
9.化简:.
10.求证:tan-tan=.
二、综合训练题
11.+32cos212°的值为( )
A.4 B.8 C.16 D.32
12.化简:=________.
三、能力提升题
13.设α∈,β∈,且=,则( )
A.2α+β= B.2α-β=
C.α+2β= D.α-2β=
14.化简得( )
A.2+sinα B.2+
C.2 D.2+
15.tan 20°+4sin 20°=________.
5.5.2简单的三角恒等变换(一)
参考答案
1、答案 D
解析 由<α<π可知<<,故sin ===.
2、答案 C
解析 方法一 因为sin α=,cos α=,所以tan ==-2.
方法二 因为sin α=>0,cos α=>0,所以α的终边落在第一象限,的终边落在第一或第三象限,
所以tan >0,故tan ===-2.
3、答案 D
解析 ∵-3π<α<-,∴-<<-.
∴sin >0,cos <0,====sin -cos .
4、答案 C
解析 原式==,因为0<1<,故原式=cos 1.
5、答案 C
解析 a=sin 30°cos 6°-cos 30°sin 6°=sin(30°-6°)=sin 24°,b=2sin 13°·cos 13°=sin 26°,c=sin 25°,
y=sin x在0°≤x≤90°时上单调递增,∴a6、答案 [cos(A+B)+sin(A-B)]
解析 sincos==[cos(A+B)+sin(A-B)].
7、答案 2
解析 原式===2.
8、答案
解析 因为β∈,cos β=-,则sin β=,tan===.
因为α∈,β∈,故α+β∈,
从而cos(α+β)=-=-=-,
所以sin α=sin[(α+β)-β]=sin(α+β)cos β-cos(α+β)sin β=×-×=.
9、解: 原式=2+
=2+=2|sin 4+cos 4|+2|cos 4|.
由于π<4<,∴sin 4<0,cos 4<0,sin 4+cos 4<0,
∴原式=-2(sin 4+cos 4)-2cos 4=-2sin 4-4cos 4.
10、证明: 法一:(由左推右)tan-tan=-=
====.
法二:(由右推左)
===-=tan-tan.
11、答案 C
解析 原式=+16·(2cos212°-1)+16=+16cos 24°+16
=+16cos 24°+16=+16cos 24°+16
=+16cos 24°+16=16.
12、答案 tan
解析 原式====tan .
13、答案 B
解析 由题意得sin α-sin αsin β=cos αcos β,sin α=cos(α-β),∴cos=cos(α-β).
∵-α∈,α-β∈,∴-α=α-β或-α+α-β=0(舍去),∴2α-β=.
14、答案 2
解析 原式=1+2sincos+1-cos=2+sinα-cos=2+sinα-sinα=2.
15、答案
解析 原式=+4sin 20°==
===.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
5.5.2简单的三角恒等变换(一)
班级 姓名
学习目标
1.通过二倍角公式的变形公式推导出半角的正弦、余弦、正切公式.
2.了解半角公式的结构形式,并能利用半角公式解决简单的求值问题.
3.掌握两角和、差的正、余弦公式,通过积化和差、和差化积进行简单的化简、求值、证明.
学习过程
自学指导 自学检测及课堂展示
阅读教材,完成右边的内容 1、二倍角公式三角函数公式简记正弦sin 2α= S2α余弦cos 2α= = = C2α正切tan 2α= T2α2、半角公式(1)sin=± , (2)cos=± , (3)tan=± ,(4)tan===, tan===.
半角公式的运用 例1、已知θ∈且sin θ=,求sin ,cos ,tan 的值.
带根号形式的化简 例2、已知π<α<,化简:+.变式1、化简:(1)+=________.(2)=________.
和差化积与积化和差 例3、证明:(1)sin αcos β=[sin(α+β)+sin(α-β)]; (2)sin θ+sin φ=2sin cos ; INCLUDEPICTURE "D:\\源文件\\2021\\同步\\数学\\人教A版必修第一册\\左括.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\苏德亭2021\\同步\\数学\\数学 人教A版 必修第一册\\新建文件夹\\左括.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\苏德亭2021\\同步\\数学\\数学 人教A版 必修第一册\\新建文件夹\\左括.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\苏德亭2021\\同步\\数学\\数学 人教A版 必修第一册\\新建文件夹\\左括.TIF" \* MERGEFORMATINET INCLUDEPICTURE "\\\\苏德亭\\d\\苏德亭2021\\同步\\数学\\数学 人教A版 必修第一册\\新建文件夹\\左括.TIF" \* MERGEFORMATINET 知识梳理 INCLUDEPICTURE "D:\\源文件\\2021\\同步\\数学\\人教A版必修第一册\\右括.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\苏德亭2021\\同步\\数学\\数学 人教A版 必修第一册\\新建文件夹\\右括.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\苏德亭2021\\同步\\数学\\数学 人教A版 必修第一册\\新建文件夹\\右括.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\苏德亭2021\\同步\\数学\\数学 人教A版 必修第一册\\新建文件夹\\右括.TIF" \* MERGEFORMATINET INCLUDEPICTURE "\\\\苏德亭\\d\\苏德亭2021\\同步\\数学\\数学 人教A版 必修第一册\\新建文件夹\\右括.TIF" \* MERGEFORMATINET 1.积化和差sin αcos β=[sin(α+β)+sin(α-β)]; cos αsin β=[sin(α+β)-sin(α-β)];cos αcos β=[cos(α+β)+cos(α-β)]; sin αsin β=-[cos(α+β)-cos(α-β)].2.和差化积sin θ+sin φ=2sin cos ; sin θ-sin φ=2cos sin ;cos θ+cos φ=2cos cos ; cos θ-cos φ=-2sin sin .
三角恒等式的证明 例4、求证:=sin 2α.
课后作业
一、基础训练题
1.已知cos α=-,<α<π,则sin 等于( )
A.- B.
C.- D.
2.已知sin α=,cos α=,则tan 等于( )
A.2- B.2+
C.-2 D.±(-2)
3.设-3π<α<-,化简的结果是( )
A.sin +cos B.-cos -sin
C.cos -sin D.sin -cos
4.化简的结果是( )
A.-cos 1 B.cos 1
C.cos 1 D.-cos 1
5.设a=cos 6°-sin 6°,b=2sin 13°cos 13°,c=,则有( )
A.c
7.= .
8.已知α∈,β∈,cos β=-,sin(α+β)=,则tan= ,sin α= .
9.化简:.
10.求证:tan-tan=.
二、综合训练题
11.+32cos212°的值为( )
A.4 B.8 C.16 D.32
12.化简:=________.
三、能力提升题
13.设α∈,β∈,且=,则( )
A.2α+β= B.2α-β=
C.α+2β= D.α-2β=
14.化简得( )
A.2+sinα B.2+
C.2 D.2+
15.tan 20°+4sin 20°=________.
5.5.2简单的三角恒等变换(一)
参考答案
1、答案 D
解析 由<α<π可知<<,故sin ===.
2、答案 C
解析 方法一 因为sin α=,cos α=,所以tan ==-2.
方法二 因为sin α=>0,cos α=>0,所以α的终边落在第一象限,的终边落在第一或第三象限,
所以tan >0,故tan ===-2.
3、答案 D
解析 ∵-3π<α<-,∴-<<-.
∴sin >0,cos <0,====sin -cos .
4、答案 C
解析 原式==,因为0<1<,故原式=cos 1.
5、答案 C
解析 a=sin 30°cos 6°-cos 30°sin 6°=sin(30°-6°)=sin 24°,b=2sin 13°·cos 13°=sin 26°,c=sin 25°,
y=sin x在0°≤x≤90°时上单调递增,∴a
解析 sincos==[cos(A+B)+sin(A-B)].
7、答案 2
解析 原式===2.
8、答案
解析 因为β∈,cos β=-,则sin β=,tan===.
因为α∈,β∈,故α+β∈,
从而cos(α+β)=-=-=-,
所以sin α=sin[(α+β)-β]=sin(α+β)cos β-cos(α+β)sin β=×-×=.
9、解: 原式=2+
=2+=2|sin 4+cos 4|+2|cos 4|.
由于π<4<,∴sin 4<0,cos 4<0,sin 4+cos 4<0,
∴原式=-2(sin 4+cos 4)-2cos 4=-2sin 4-4cos 4.
10、证明: 法一:(由左推右)tan-tan=-=
====.
法二:(由右推左)
===-=tan-tan.
11、答案 C
解析 原式=+16·(2cos212°-1)+16=+16cos 24°+16
=+16cos 24°+16=+16cos 24°+16
=+16cos 24°+16=16.
12、答案 tan
解析 原式====tan .
13、答案 B
解析 由题意得sin α-sin αsin β=cos αcos β,sin α=cos(α-β),∴cos=cos(α-β).
∵-α∈,α-β∈,∴-α=α-β或-α+α-β=0(舍去),∴2α-β=.
14、答案 2
解析 原式=1+2sincos+1-cos=2+sinα-cos=2+sinα-sinα=2.
15、答案
解析 原式=+4sin 20°==
===.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
