辽宁省大连市重点中学2023-2024学年高一上学期12月学情反馈数学试题 (含答案)
文档属性
| 名称 | 辽宁省大连市重点中学2023-2024学年高一上学期12月学情反馈数学试题 (含答案) | 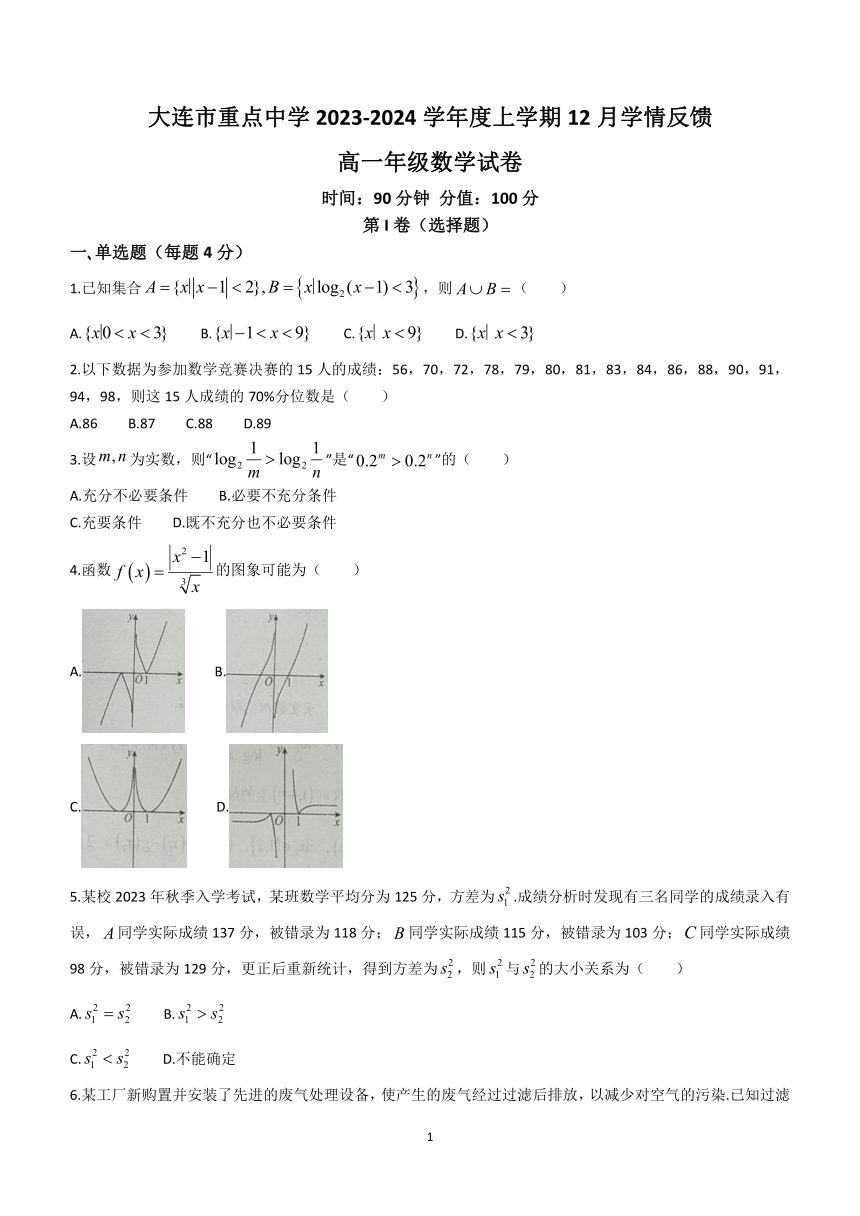 | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-09 15:20:37 | ||
图片预览



文档简介
大连市重点中学2023-2024学年度上学期12月学情反馈
高一年级数学试卷
时间:90分钟 分值:100分
第I卷(选择题)
一 单选题(每题4分)
1.已知集合,则( )
A. B. C. D.
2.以下数据为参加数学竞赛决赛的15人的成绩:56,70,72,78,79,80,81,83,84,86,88,90,91,94,98,则这15人成绩的70%分位数是( )
A.86 B.87 C.88 D.89
3.设为实数,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.函数的图象可能为( )
A. B.
C. D.
5.某校2023年秋季入学考试,某班数学平均分为125分,方差为.成绩分析时发现有三名同学的成绩录入有误,同学实际成绩137分,被错录为118分;同学实际成绩115分,被错录为103分;同学实际成绩98分,被错录为129分,更正后重新统计,得到方差为,则与的大小关系为( )
A. B.
C. D.不能确定
6.某工厂新购置并安装了先进的废气处理设备,使产生的废气经过过滤后排放,以减少对空气的污染.已知过滤过程中废气的污染物数量(单位:)与过滤时间(单位:)的关系为(是正常数).若经过过滤后消除了的污染物,则污染物减少大约需要( )(参考数据:)
A. B. C. D.
7.若实数满足,其中,则下列结论正确的是( )
A. B.
C. D.
8.已知函数若(互不相等),则的取值范围是( )(注:函数在上单调递减,在上单调递增)
A. B. C. D.
二 多选题(每题4分,漏选2分,错选0分)
9.小张于2017年底贷款购置了一套房子,根据家庭收入情况,小张选择了10年期的等额本息的还贷方式(每月还款数额相等),2021年底贷款购置了一辆小汽车,且截至2022年底,他没有再购买第二套房子.如图是2018年和2022年小张的家庭的各项支出占家庭收入的比例分配图.根据以上信息,判断下列结论中正确的是( )
A.小张一家2022年的家庭收入比2018年增加了1倍
B.小张一家2022年用于娱乐的支出费用为2018年的5倍
C.小张一家2022年用于饮食的支出费用小于2018年
D.小张一家2022年用于车贷的支出费用小于2018年用于饮食的支出费用
10.已知函数,下列结论不正确的是( )
A.若,则
B.
C.若,则或
D.若方程有两个不同的实数根,则
三 填空题(每题4分)
11.甲 乙两名运动员进入男子羽毛球单打决赛,假设比赛打满3局,赢得2局或3局者胜出,用计算机产生1-5之间的随机数,当出现随机数1,2,3时,表示一局比赛甲获胜;否则,乙获胜.由于要比赛3局,所以每3个随机数为一组,产生20组随机数:
据此估计甲获得冠军的概率为__________;
12.已知且的图象过点,其反函数的图象过点,则__________.
13.我市男子乒乓球队为备战下届市运会,在某训练基地进行封闭时训练,甲 乙两队队员进行对抗赛,每局依次轮流发球;连续赢两个球者获胜.通过分析甲 乙过去对抗赛的数据知,甲发球甲赢的概率为,乙发球甲赢的概率为,不同球的结果互不影响.已知某局甲先发球,该局打四个球,甲赢的概率是__________.
14.已知函数,且在区间上单调递增,则的取值范围__________.
四 解答题(15,16题每题10分,17,18题每题12分)
15.已知幂函数在定义域上不单调.
(1)求的值.
(2)若,求实数的取值范围.
16.制成奶嘴的主要材质是橡胶,在加工过程中,可能会残留一些未挥发完全的溶剂,以及橡胶本身含有的化合物等.因为奶嘴直接接触食物和婴儿口腔,使用过程中,挥发性物质的溶出会污染奶质,甚至通过消化道被宝宝身体吸收,长期潜伏积累,对免疫力尚未健全的婴幼儿会危害甚大,因此我国对奶嘴和安抚奶嘴的挥发性物质做了规定,要求其含量不得超过0.5%.某婴儿用品的生产商为了测量某新产品的挥发性物质含量,从试生产的产品中随机抽取100个,得到如下频率分布直方图:注:以频率作为概率,该婴儿用品的生产商规定挥发性物质含量<18‰为合格产品.
(1)根据频率分布直方图,求这100个奶嘴的挥发性物质含量的中位数;
(2)为了解产品不合格的原因,用分层抽样的方法从与中抽取6个进行分析,然后从这6个中抽取2个进一步实验,求在与中各有一个的概率;
(3)若这100个奶嘴的挥发性物质含量的平均值大于16,则需进行技术改进,试问该新产品是否需要技术改进?
17.已知函数.
(1)求函数在区间上的最小值;
(2)若对,使得成立,求实数的取值范围.
18.定义:如果函数在定义域内给定区间上存在,满足:,则称函数是上的“平均值函数”,是它的平均值点.
(1)函数是否是上的“平均值函数”,如果是请求出它的平均值点;如果不是,请说明理由;
(2)现有函数是上的平均值函数,求实数的取值范围.
数学答案
1.B 2.C 3.A 4.A 5.C 6.B 7.D 8.D 9.AD 10.ABC
11./ 12. 13. 14.
15.(1)(2)或
【详解】(1)由题意,解得或,
当时,,函数在上单调递增,不合题意;
当时,,函数的定义域为,
函数在上单调递减,在上单调递减,但,
所以函数在定义域上不单调,符合题意,所以.
(2)因为函数的定义域为,关于原点对称,且,所以为奇函数,因为,可得,即,
而在上递减且恒负,在上递减且恒正,所以或或,
解得或.
16.(1);(2);(3)该产品需要进行技术改进.
【详解】解:(1)挥发性物质含量位于的频率为,
挥发性物质含量位于的频率为,
所以这100个奶嘴的挥发性物质含量的中位数位于区间,
设中位数为,则,解得;
(2)组的奶嘴的个数为,组的奶嘴的个数为,
所以从组中抽取个,从组中抽取个,
记组中抽取的5个分别为a,b,c,d,e,组中抽取的一个为f,
则从6个中抽取2个的所有情况如下:,,,,,,,,,,,,,,
共15种情况,其中在与中各有1个的有,,,,共5种情况,所以所求的概率;
(3)因为,
故该产品需要进行技术改进.
17.(1)6(2)
【详解】(1)令,因为,所以,则可化为,,因为,当且仅当,即,时,等号成立,所以时,取最小值6.
(2)由(1),,因为,,使得成立,所以,使得成立,即,使得成立,令,因为,,
所以,使得成立,因为当,,
当,即时,取最大值2,所以.
18.(1)函数是上的“平均值函数”,0是它的平均值点
(2)
【详解】(1)函数是上的“平均值函数”,理由如下:
,设是它的平均值点.,则有解得:.
∴函数是上的“平均值函数”,0是它的平均值点.
(2)由题意得:,设是它的平均值点,
∴,即,整理得:.
令,则有解.
法一:令,
①当在内有一个实根时,,解得.
②当在内有两个不等的实根时,,可得,故.
综上所述:.
法二:整理得,
①当,即时,解得(矛盾),故.
②当,即时,整理得:
令在上单调递增,
,即..
高一年级数学试卷
时间:90分钟 分值:100分
第I卷(选择题)
一 单选题(每题4分)
1.已知集合,则( )
A. B. C. D.
2.以下数据为参加数学竞赛决赛的15人的成绩:56,70,72,78,79,80,81,83,84,86,88,90,91,94,98,则这15人成绩的70%分位数是( )
A.86 B.87 C.88 D.89
3.设为实数,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.函数的图象可能为( )
A. B.
C. D.
5.某校2023年秋季入学考试,某班数学平均分为125分,方差为.成绩分析时发现有三名同学的成绩录入有误,同学实际成绩137分,被错录为118分;同学实际成绩115分,被错录为103分;同学实际成绩98分,被错录为129分,更正后重新统计,得到方差为,则与的大小关系为( )
A. B.
C. D.不能确定
6.某工厂新购置并安装了先进的废气处理设备,使产生的废气经过过滤后排放,以减少对空气的污染.已知过滤过程中废气的污染物数量(单位:)与过滤时间(单位:)的关系为(是正常数).若经过过滤后消除了的污染物,则污染物减少大约需要( )(参考数据:)
A. B. C. D.
7.若实数满足,其中,则下列结论正确的是( )
A. B.
C. D.
8.已知函数若(互不相等),则的取值范围是( )(注:函数在上单调递减,在上单调递增)
A. B. C. D.
二 多选题(每题4分,漏选2分,错选0分)
9.小张于2017年底贷款购置了一套房子,根据家庭收入情况,小张选择了10年期的等额本息的还贷方式(每月还款数额相等),2021年底贷款购置了一辆小汽车,且截至2022年底,他没有再购买第二套房子.如图是2018年和2022年小张的家庭的各项支出占家庭收入的比例分配图.根据以上信息,判断下列结论中正确的是( )
A.小张一家2022年的家庭收入比2018年增加了1倍
B.小张一家2022年用于娱乐的支出费用为2018年的5倍
C.小张一家2022年用于饮食的支出费用小于2018年
D.小张一家2022年用于车贷的支出费用小于2018年用于饮食的支出费用
10.已知函数,下列结论不正确的是( )
A.若,则
B.
C.若,则或
D.若方程有两个不同的实数根,则
三 填空题(每题4分)
11.甲 乙两名运动员进入男子羽毛球单打决赛,假设比赛打满3局,赢得2局或3局者胜出,用计算机产生1-5之间的随机数,当出现随机数1,2,3时,表示一局比赛甲获胜;否则,乙获胜.由于要比赛3局,所以每3个随机数为一组,产生20组随机数:
据此估计甲获得冠军的概率为__________;
12.已知且的图象过点,其反函数的图象过点,则__________.
13.我市男子乒乓球队为备战下届市运会,在某训练基地进行封闭时训练,甲 乙两队队员进行对抗赛,每局依次轮流发球;连续赢两个球者获胜.通过分析甲 乙过去对抗赛的数据知,甲发球甲赢的概率为,乙发球甲赢的概率为,不同球的结果互不影响.已知某局甲先发球,该局打四个球,甲赢的概率是__________.
14.已知函数,且在区间上单调递增,则的取值范围__________.
四 解答题(15,16题每题10分,17,18题每题12分)
15.已知幂函数在定义域上不单调.
(1)求的值.
(2)若,求实数的取值范围.
16.制成奶嘴的主要材质是橡胶,在加工过程中,可能会残留一些未挥发完全的溶剂,以及橡胶本身含有的化合物等.因为奶嘴直接接触食物和婴儿口腔,使用过程中,挥发性物质的溶出会污染奶质,甚至通过消化道被宝宝身体吸收,长期潜伏积累,对免疫力尚未健全的婴幼儿会危害甚大,因此我国对奶嘴和安抚奶嘴的挥发性物质做了规定,要求其含量不得超过0.5%.某婴儿用品的生产商为了测量某新产品的挥发性物质含量,从试生产的产品中随机抽取100个,得到如下频率分布直方图:注:以频率作为概率,该婴儿用品的生产商规定挥发性物质含量<18‰为合格产品.
(1)根据频率分布直方图,求这100个奶嘴的挥发性物质含量的中位数;
(2)为了解产品不合格的原因,用分层抽样的方法从与中抽取6个进行分析,然后从这6个中抽取2个进一步实验,求在与中各有一个的概率;
(3)若这100个奶嘴的挥发性物质含量的平均值大于16,则需进行技术改进,试问该新产品是否需要技术改进?
17.已知函数.
(1)求函数在区间上的最小值;
(2)若对,使得成立,求实数的取值范围.
18.定义:如果函数在定义域内给定区间上存在,满足:,则称函数是上的“平均值函数”,是它的平均值点.
(1)函数是否是上的“平均值函数”,如果是请求出它的平均值点;如果不是,请说明理由;
(2)现有函数是上的平均值函数,求实数的取值范围.
数学答案
1.B 2.C 3.A 4.A 5.C 6.B 7.D 8.D 9.AD 10.ABC
11./ 12. 13. 14.
15.(1)(2)或
【详解】(1)由题意,解得或,
当时,,函数在上单调递增,不合题意;
当时,,函数的定义域为,
函数在上单调递减,在上单调递减,但,
所以函数在定义域上不单调,符合题意,所以.
(2)因为函数的定义域为,关于原点对称,且,所以为奇函数,因为,可得,即,
而在上递减且恒负,在上递减且恒正,所以或或,
解得或.
16.(1);(2);(3)该产品需要进行技术改进.
【详解】解:(1)挥发性物质含量位于的频率为,
挥发性物质含量位于的频率为,
所以这100个奶嘴的挥发性物质含量的中位数位于区间,
设中位数为,则,解得;
(2)组的奶嘴的个数为,组的奶嘴的个数为,
所以从组中抽取个,从组中抽取个,
记组中抽取的5个分别为a,b,c,d,e,组中抽取的一个为f,
则从6个中抽取2个的所有情况如下:,,,,,,,,,,,,,,
共15种情况,其中在与中各有1个的有,,,,共5种情况,所以所求的概率;
(3)因为,
故该产品需要进行技术改进.
17.(1)6(2)
【详解】(1)令,因为,所以,则可化为,,因为,当且仅当,即,时,等号成立,所以时,取最小值6.
(2)由(1),,因为,,使得成立,所以,使得成立,即,使得成立,令,因为,,
所以,使得成立,因为当,,
当,即时,取最大值2,所以.
18.(1)函数是上的“平均值函数”,0是它的平均值点
(2)
【详解】(1)函数是上的“平均值函数”,理由如下:
,设是它的平均值点.,则有解得:.
∴函数是上的“平均值函数”,0是它的平均值点.
(2)由题意得:,设是它的平均值点,
∴,即,整理得:.
令,则有解.
法一:令,
①当在内有一个实根时,,解得.
②当在内有两个不等的实根时,,可得,故.
综上所述:.
法二:整理得,
①当,即时,解得(矛盾),故.
②当,即时,整理得:
令在上单调递增,
,即..
同课章节目录
