14.1.4整式的乘法 课件(4课时、共80张PPT) 2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 14.1.4整式的乘法 课件(4课时、共80张PPT) 2023-2024学年人教版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 474.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 00:00:00 | ||
图片预览










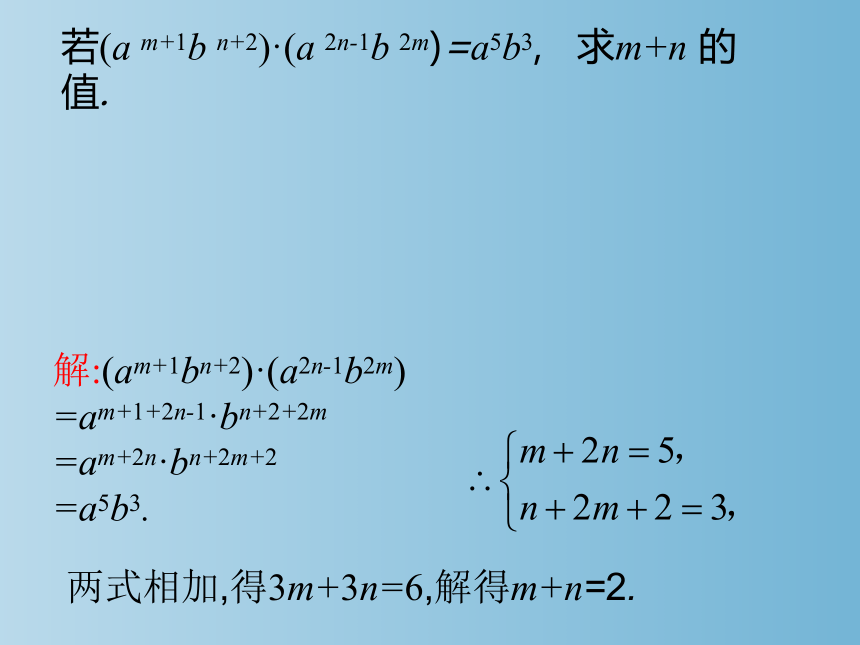
文档简介
(共80张PPT)
八年级数学·上 新课标 [人]
14.1.4 整式的乘法(1)
第十四章 整式的乘法与因式分解
我们在前面学习过了整式的加减运算,还记得整式的加减法是如何运算的吗
其实整式的运算就像数的运算,
除了加减法,还有整式的乘法、整式的
除法.
光的速度约是3×105 km/s,太阳光照射到地球上需要的时间约是5×102 s,你知道地球与太阳的距离约是多少吗
一、法则的探究
(3×105)×(5×102).
(1)怎样计算(3×105)×(5×102)
计算过程中用到了哪些运算律及运算性质
(2)如果将上式中的数字改为字母,比如ac5·bc2,怎样计算这个式子
(1)(3×105)×(5×102)=(3×5)×(105×102)
=15×107
=1.5×108.
运用乘法的交换律和结合律
利用同底数幂的乘法法则进行计算
写成科学记数法的形式
(2)ac5·bc2=(a·b)·(c5·c2)
=abc5+2
=abc7.
运用乘法的交换律和结合律
利用同底数幂的乘法法则进行计算
得出结果
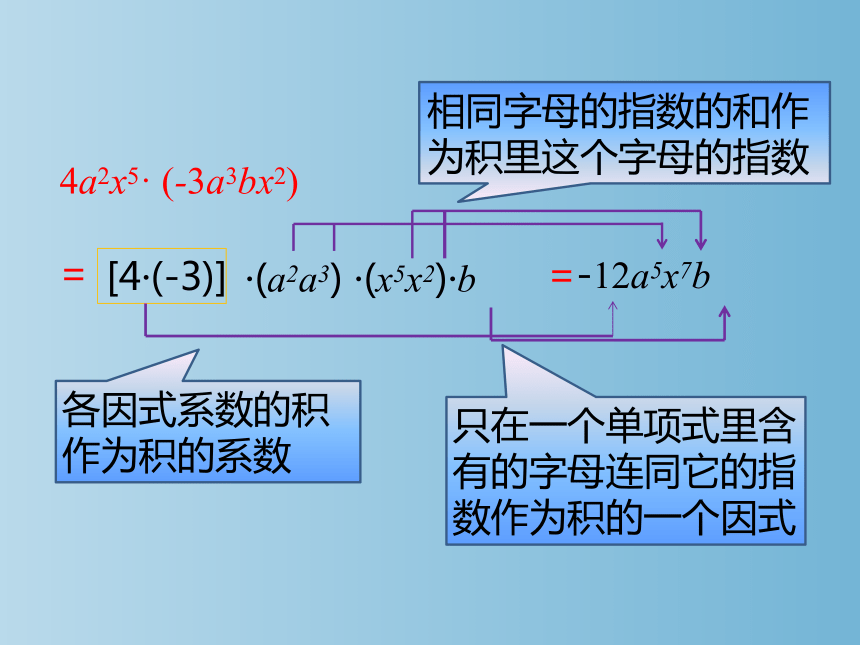
如何计算4a2x5· (-3a3bx2) 由此你能总结单项式与单项式相乘的乘法法则吗
4a2x5· (-3a3bx2)
=
[4·(-3)]
·(a2a3) ·(x5x2)·b
=-12a5x7b
相同字母的指数的和作
为积里这个字母的指数
各因式系数的积
作为积的系数
只在一个单项式里含有的字母连同它的指数作为积的一个因式
单项式与单项式怎样相乘
单项式与单项式相乘,利用乘法交换律和结合律,把它们的系数、同底数幂分别相乘,对于只在一个单项式中出现的字母连同它的指数不变,一起作为积的因式.
(1)积的系数是各因式的系数的积.
(2)相同字母按照同底数幂的运算
法则进行计算.
(3)只在一个因式中出现的字母,
连同它的指数一起作为积的一个
因式.
(4)上述法则对于三个以上
单项式相乘同样适用.
(5)结果仍是单项式.
计算.
(1)(-5a2b)(-3a); (2)(2x)3(-5x y2).
解: (1)(-5a 2b)(-3a)
=[(-5)×(-3)](a 2·a )·b
=15a 3b.
(2)(2x )3(-5x y 2)
=8x 3·(-5x y 2)
=[8×(-5)](x 3·x )·y 2
=-40x 4y 2.
若(a m+1b n+2)·(a 2n-1b 2m)=a5b3, 求m+n 的值.
解:(am+1bn+2)·(a2n-1b2m)
=am+1+2n-1·bn+2+2m
=am+2n·bn+2m+2
=a5b3.
两式相加,得3m+3n=6,解得m+n=2.
1.根据单项式乘单项式的法则,
在进行计算时,可按照如下步骤进行:
(1)系数相乘——确定积的系数,在相乘时,要注意符号;
(2)相同字母相乘——底数不变,指数相加;
(3)只在一个单项式中含有的字母——
连同字母的指数写在乘积中.
小结
2.在进行单项式的乘法时要
注意以下问题:
(1)先把各因式的系数组成一组,积的系数等于各因式系数的积,先确定符号,再计算绝对值;
(2)相同字母相乘时,利用同底数幂的乘法法则“底数不变,指数相加”;
(3)对于只在一个单项式中含有
的字母,则连同它的指数一起写在乘
积里,应特别注意不要漏掉这部分因式;
(4)单项式乘法中,如有积的乘方,就要按积的乘方法则先求出积的乘方,再进行乘法计算;
(5)对于三个或三个以上的单项式相乘时,法则仍然适用;
(6)单项式乘以单项式,结果仍是单
项式.
B
1.计算(2a2)3· a的结果是 ( )
A.3a7 B.4a7 C.a7 D.4a6
解析:原式=8a6· a=4a7.
B
2.计算3x 3·2x 2的结果是 ( )
A.5x 5 B.6x 5 C.6x 6 D.6x 9
3.下列运算正确的是 ( )
A.a3+a4=a7 B.2a3·a4=2a7
C.(2a4)3=8a7 D.a8-a2=a6
B
4.计算.(1)(-7x4yz2)·(-4xz3);
解:(1)原式=28x5yz5.
(2)原式=14x4y2z.
(3)原式= x6y3·(-4xy)
=- x7y4.
八年级数学·上 新课标 [人]
14.1.4 整式的乘法(2)
第十四章 整式的乘法与因式分解
为了扩大绿地面积,要把街心花园的一块长p m,宽b m的长方形绿地,向两边分别加宽a m和c m,你能用几种方法表示扩大后的绿地面积 不同的表示方法之间有什么关系 如何从数学的角度认识不同的表示方法之间的关系
一、问题探究
(1)扩大后绿地的长和宽分别是多少
长为 m;宽为 m.
(2)根据长方形的面积=长×宽,你能得到的式子是: ①.
(3)利用分割法,可以把扩大后的面积看成几部分面积的和.
如上图,面积可以表示为 ②.
(4)这三部分的面积可以怎么表示
(5)①和②都表示扩大后绿地的面积,它们是什么关系呢
由于①和②都表示同一个量,所以这两个式子相等,即p(a+b+c)=pa+pb+pc.
用p乘以括号里的每一项,再把所得的积相加.
(6)对于这个等式,同学们想一想:你能用乘法分配律说明这个等式吗
p和a+b+c分别是什么样的式子
p是单项式,a+b+c是多项式,这个乘法是单项式与多项式的乘法,请同学们试着总结一下单项式与多项式相乘的法则.
一般地,单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
因为代数式中的字母都表示数,所以单项式可以看做是一个数,多项式可以看做是若干个数的和.因此,单项式与多项式相乘,可以利用乘法分配律,用单项式去乘多项式的每一项,从而转化为单项式的乘法,最后再把所得的积相加即可.
(1)在运用单项式与多项式相乘
的法则时要注意各项的符号问题,
且此法则是由乘法分配律推导出
来的,所以单项式与多项式相乘可
按乘法分配律进行计算.
(2)等式的左边是积,等式的右边
是和.
(3)单项式与多项式相乘所得的
结果是一个多项式,它的项数等
于原来多项式的项数.
计算:
(1)(-4x2)(3x+1);
解:
(1)原式=(-4x2)·3x+(-4x2)×1
=(-4×3)(x2·x)+(-4x2)
=-12x3-4x2.
(2)原式=
解: 原式=-x 3y+3x 2y 2-10x 3y+10x 2y 2
=-11x 3y+13x 2y 2.
化简:
解方程:8x (5-x )=19-2x (4x-3).
40x-8x2=19-8x2+6x
40x-6x=19
34x=19
解:8x(5-x)=19-2x(4x-3)
1.单项式乘以多项式的
法则:
一般地,单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
小结
2.运用单项式乘以多项式的法
则时,应注意以下几个问题:
(1)单项式与多项式相乘实质上是转化为单项式乘以单项式.
(2)用单项式去乘多项式中的每一项时,不能漏乘.
(3)注意确定积的符号.
(4)多项式中有几项,结果就是几项.
(5)多项式中的每一项都包括它前面
的符号.
C
1.计算2x(3x 2+1),正确的结果是 ( )
A.5x 3+2x B.6x 3+1
C.6x 3+2x D.6x 2+2x
A
2.-5x·(2x 2-x+3)的计算结果为 ( )
A.-10x 3+5x 2-15x
B.-10x 3-5x 2+15x
C.10x 3-5x 2-15x
D.-10x 3+5x 2-3
3.计算(-2a 3+3a 2-4a)(-5a 5)等于 ( )
A.10a 15-15a 10+20a 5
B.-7a 8-2a 7-9a 6
C.10a 8+15a 7-20a 6
D.10a 8-15a 7+20a 6
D
4.计算
八年级数学·上 新课标 [人]
14.1.4 整式的乘法(3)
第十四章 整式的乘法与因式分解
单项式乘多项式运算法则是什么?
整式的乘法实际上就是:
单项式×单项式
单项式×多项式
多项式×多项式
如图所示,为了扩大街心花园的绿地面积,把一块原长a m、宽p m的长方形绿地,加长了b m,加宽了q m.你能用几种方法求出扩大后的绿地面积
你能根据题意抽象出图形吗?
一、法则的推导
1.长方形的长是 ,宽是 .
根据长方形的面积公式面积可表示为:
。
a+b
p+q
(a+b)·(p+q)
2.如果把长方形分成两部分,一个一边是a 的长方形和一个一边是b 的长方形,则面积可表示为 .
a(p+q)+b(p+q)
3.如果分成四部分,则面积为 .如下图所示.
ap+aq+bp+bq
4.观察以上几个算式,你从计算过程中发现了什么
(a+b)(p+q)=a(p+q)+b(p+q)
=ap+aq+bp+bq.
多项式乘以多项式
5.想一想:上面的乘法属于哪一种运算
(a+b)+(p+q)=ap+aq+bp+bq.
上面的等式提供了多项式与多项式相乘的方法.
总体上看,(a+b)(p+q)的结果可以看成由a+b 的每一项乘p+q 的每一项,再把所得的积相加而得到的,即:
一般地,多项式与多项式相乘,先用一个多项式的每一项去乘另一个多项式的每一项,再把所得的积相加.
整式的乘法中我们学习了三个运算法则,它们都是由乘法的运算律推理出来的,为方便记忆,特归纳如下:
总结
乘法
在这三个法则中,单项式乘单项式的法则是基础、是关键.
解: (1)(3x+1)(x+2)
= (3x )· x+(3x )×2+1·x+1×2
= 3x2+6x+x+2
= 3x2+7x+2.
例6:计算:
(1)(3x+1)(x+2); (2)(x- 8y )(x-y );
(3)(x+y )(x 2 -xy+y 2).
(2)(x-8y )(x-y )
=x 2-xy-8xy+8y 2
=x 2-9xy+8y 2 .
(3)(x+y)(x 2 -xy+y 2)
=x 3-x 2y+xy 2+x 2y-xy 2 +y 3
=x 3 +y 3.
例(x 2-3x+n)(x 2+mx+8)的结果中不含x 2和x 3的项,求m,n 的值.
∵不含x 2和x 3的项,
∴m-3=0,8-3m+n=0.
∴m=3,n=1.
解: (x 2-3x+n)(x 2+mx+8)=x 4+mx 3+8x 2-3x 3-3mx 2-24x+nx 2+nmx+8n
=x 4+(m-3)x 3+(8-3m+n)x 2-(24-mn)x+8n,
1.多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
小结
2.运用法则时注意以下两点:
(1)相乘时,按一定顺序进行,必须做
到不重不漏.
(2)多项式与多项式相乘,仍得多项式,
在合并同类项之前,积的项数应等于原
多项式的项数之积.
D
1.下列各式中,计算结果是x 2+7x-18的是 ( )
A.(x-1)(x+18) B.(x+2)(x+9)
C.(x-3)(x+6) D.(x-2)(x+9)
A
2.(x-1)(2x+3)的计算结果是 ( )
A.2x 2+x-3 B.2x 2-x-3
C.2x 2-x+3 D.x 2-2x-3
3.若(x-2)(x+a)=x 2+bx-2,则a+b等于 ( )
A.-1 B.0
C.1 D.2
B
4.计算.
(1)(3x+2)(2x-1);
(2)(2x-8y )(x-3y );
(3)(2m-n)(3m- 4n);
(4)(2x 2-1)(2x-3);
(5)(2a-3)2;
(6)(3x-2)(3x+2)-6(x 2+x-1).
(6)原式=(3x)2+6x-6x-4-6x 2-6x+6
=3x 2-6x+2.
解: (1)原式=3x·2x-3x+2×2x-2=6x 2+x-2.
(2)原式=2x·x-2x·3y-8y·x+8y·3y
=2x 2-14xy+24y 2.
(3)原式=2m·3m-2m·4n-3m·n+n·4n
=6m2-11mn+4n 2.
(4)原式=2x 2·2x+2x 2×(-3)-2x+3
=4x 3-6x 2-2x+3.
(5)原式=(2a-3)(2a-3)
=(2a)2-6a-6a+9=4a 2-12a+9.
八年级数学·上 新课标 [人]
14.1.4 整式的乘法(4)
第十四章 整式的乘法与因式分解
一、同底数幂的除法
2.填空:
(1)( )·28=216;
(2)( )·53=55;
(3)( )·105=107;
(4)( )·a3=a6.
1.计算:
(3)102×105; (4)a3·a3.
(1)28×28;
(2)52×53;
28
52
102
a3
(1)216÷28=( );
(2)55÷53=( );
(3)107÷105=( );
(4)a 6÷a3=( ).
从上述运算能否发现商与除数、被除数有什么关系
同底数幂相除,底数不变,指数相减.
用公式表示为am÷an=am-n(a≠0,m,n 都是正整数,且m≥n).
这里的a为什么不等于0
现在我们学的指数都是大于或等于零的数,所以m≥n.
(因为0的任何次幂都是0,而0不能作除数,所以a≠0)
当m=n时,am÷an=a0=1.这样我们就得到了a0=1(a≠0),这就是说,任何不等于0的数的0次幂都等于1.
同底数幂的除法的关键在
于底数,底数一定相同,并且
二者是相除关系,这样指数才
能相减,否则不能运用此
法则.
同底数幂的除法可以从
加与减、乘与除互为逆运算
的角度来理解,在运算上常见
的错误有:(1)指数运算混乱;
(2)底数确定不对;(3)系数计
算错误;(4)运算顺序不对.
木星的质量约是1.90×1024吨,地球的质量约是5.98×1021吨.你知道木星的质量约为地球质量的多少倍吗
二、单项式除以单项式
与多项式除以单项式
这是除法运算,木星的质量约为地球质量的(1.90×1024)÷(5.98×1021)倍.
(1)计算(1.90×1024)÷(5.98×1021).
(3)你能根据(2)说说单项式除以单项
式的运算法则吗
(2)你能利用(1)中的方法计算下列各式吗
8a 3÷2a ; 6x 3y÷3xy ; 12a 3b 2x 3÷3ab 2.
1.从乘法与除法互为逆运算的角度去考虑.
(1)我们可以想象5.98×1021·( )
=1.90×1024.根据单项式与单项式相乘的运算法则:单项式与单项式相乘,是把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变作为积的因式.
所求单项式的系数乘
以5.98等于1.90,所以所求单项式系数为1.90÷5.98≈0.318,所求单项式的幂值部
分应包含1024÷1021即103,由此可知5.98×1021·(0.318×103) ≈1.90×1024.
所以(1.90×1024)÷(5.98×1021)
≈0.318×103;
(2)可以想象2a·( )=8a3,根据单项式与单项式相乘的运算法则,可以考虑:8÷2=4,a3÷a=a2,即2a·(4a2)=8a3.所以8a3÷2a=4a2.
同样的道理可以想象
3xy·( )=6x3y; 3ab2·( ) =12a3 b2x3.考虑到6÷3=2,x3÷x=x2,y÷y=1;12÷3=4,a3÷a=a2,b2÷b2 =1.所以得3xy·(2x2)=6x3y;
3ab2·(4a2·x3)=12a3 b2·x3.所以
6x3 y÷3xy=2x2;12a3b2x3÷3ab2 =4a2x3.
2.还可以从除法的意义去考虑.
(1)(1.90×1024)÷(5.98×1021)=
=×≈0.318×103;
(2)8a3÷2a==·=4a2;
6x3y÷3xy==··=2x2;
12a3b2x3÷3ab2==···x3=4a2x3.
总结
(1)都是单项式除以单项式;
(2)运算的结果都是把系数、同底数幂分别相除后作为商的因式;对于只在一个被除式中含有的字母,则连同它的指数一起作为商的一个因式;
(3)单项式相除是在同底数幂的除法的基础上进行的.
(1)(am+bm)÷m ;
(2)(a 2 +ab)÷a ;
(3)(4x 2y+2xy 2)÷2xy .
再探新知计算下列各式:
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.用公式表示为(am+bm)÷m=am÷m+bm÷m=a+b.
多项式除以单项式,也可以通过“约分”导出运算性质,不过要明确约分的依据,该依据是分数的基本性质,即分子、分母同时除以一个不等于零的数,分数的值不变.
例8 计算:
(1) 28x4y2÷7x3y;
(2)-5a5b3c÷15a4b.
解:(1) 28x4y2÷7x3y
(2)-5a5b3c÷15a4b
1.同底数幂的除法.
同底数幂的除法,底数不变,指数相减.
任何不等于零的数的零次幂都等于1.
在应用同底数幂的除法时,要注意与同底数幂乘法的区别,底数可以是单项式也可以是多项式;当三个或三个以上的同底数幂相除时,同样可以适用这一性
质.
小结
2.单项式除以单项式.
关注:(1)从法则可以看出,单项式
除以单项式分为三个步骤:一是系数相除;二是同底数幂相除;三是对于被除式中含有的字母直接作为商的一个因式.
(2)计算的结果是否正确可以利用单项式的乘法验证.
3.多项式除以单项式.
说明:多项式除以单项式的实质就是转化为单项式除以单项式.
多项式除以单项式的结果仍然是多项式.
C
1.计算-12a 6÷(3a 2)的结果是 ( )
A.- 4a 3 B.- 4a 8 C.- 4a 4 D.-a 4
B
2.计算(a 3b)2÷(ab)2的结果是 ( )
A.a 3 B.a 4
C.a 3b D.a 4b
3.地球赤道长约为4×104千米,我国最长的河流——长江全长约为6.3×103千米,赤道长约等于长江长的 ( )
A.7倍 B.6倍 C.5倍 D.4倍
B
4.计算下列各题.(1)(3a2b)3·(-2ab4)2÷(6a5b3);
解:(1)(3a2b)3.(2ab4)2(6a5b3)
=27a6b3·4a2b8÷6a5b3
=108a8b11÷6a5b3=18a3b8.
=3a2b+2ab2-1.
谢 谢 观 看
八年级数学·上 新课标 [人]
14.1.4 整式的乘法(1)
第十四章 整式的乘法与因式分解
我们在前面学习过了整式的加减运算,还记得整式的加减法是如何运算的吗
其实整式的运算就像数的运算,
除了加减法,还有整式的乘法、整式的
除法.
光的速度约是3×105 km/s,太阳光照射到地球上需要的时间约是5×102 s,你知道地球与太阳的距离约是多少吗
一、法则的探究
(3×105)×(5×102).
(1)怎样计算(3×105)×(5×102)
计算过程中用到了哪些运算律及运算性质
(2)如果将上式中的数字改为字母,比如ac5·bc2,怎样计算这个式子
(1)(3×105)×(5×102)=(3×5)×(105×102)
=15×107
=1.5×108.
运用乘法的交换律和结合律
利用同底数幂的乘法法则进行计算
写成科学记数法的形式
(2)ac5·bc2=(a·b)·(c5·c2)
=abc5+2
=abc7.
运用乘法的交换律和结合律
利用同底数幂的乘法法则进行计算
得出结果
如何计算4a2x5· (-3a3bx2) 由此你能总结单项式与单项式相乘的乘法法则吗
4a2x5· (-3a3bx2)
=
[4·(-3)]
·(a2a3) ·(x5x2)·b
=-12a5x7b
相同字母的指数的和作
为积里这个字母的指数
各因式系数的积
作为积的系数
只在一个单项式里含有的字母连同它的指数作为积的一个因式
单项式与单项式怎样相乘
单项式与单项式相乘,利用乘法交换律和结合律,把它们的系数、同底数幂分别相乘,对于只在一个单项式中出现的字母连同它的指数不变,一起作为积的因式.
(1)积的系数是各因式的系数的积.
(2)相同字母按照同底数幂的运算
法则进行计算.
(3)只在一个因式中出现的字母,
连同它的指数一起作为积的一个
因式.
(4)上述法则对于三个以上
单项式相乘同样适用.
(5)结果仍是单项式.
计算.
(1)(-5a2b)(-3a); (2)(2x)3(-5x y2).
解: (1)(-5a 2b)(-3a)
=[(-5)×(-3)](a 2·a )·b
=15a 3b.
(2)(2x )3(-5x y 2)
=8x 3·(-5x y 2)
=[8×(-5)](x 3·x )·y 2
=-40x 4y 2.
若(a m+1b n+2)·(a 2n-1b 2m)=a5b3, 求m+n 的值.
解:(am+1bn+2)·(a2n-1b2m)
=am+1+2n-1·bn+2+2m
=am+2n·bn+2m+2
=a5b3.
两式相加,得3m+3n=6,解得m+n=2.
1.根据单项式乘单项式的法则,
在进行计算时,可按照如下步骤进行:
(1)系数相乘——确定积的系数,在相乘时,要注意符号;
(2)相同字母相乘——底数不变,指数相加;
(3)只在一个单项式中含有的字母——
连同字母的指数写在乘积中.
小结
2.在进行单项式的乘法时要
注意以下问题:
(1)先把各因式的系数组成一组,积的系数等于各因式系数的积,先确定符号,再计算绝对值;
(2)相同字母相乘时,利用同底数幂的乘法法则“底数不变,指数相加”;
(3)对于只在一个单项式中含有
的字母,则连同它的指数一起写在乘
积里,应特别注意不要漏掉这部分因式;
(4)单项式乘法中,如有积的乘方,就要按积的乘方法则先求出积的乘方,再进行乘法计算;
(5)对于三个或三个以上的单项式相乘时,法则仍然适用;
(6)单项式乘以单项式,结果仍是单
项式.
B
1.计算(2a2)3· a的结果是 ( )
A.3a7 B.4a7 C.a7 D.4a6
解析:原式=8a6· a=4a7.
B
2.计算3x 3·2x 2的结果是 ( )
A.5x 5 B.6x 5 C.6x 6 D.6x 9
3.下列运算正确的是 ( )
A.a3+a4=a7 B.2a3·a4=2a7
C.(2a4)3=8a7 D.a8-a2=a6
B
4.计算.(1)(-7x4yz2)·(-4xz3);
解:(1)原式=28x5yz5.
(2)原式=14x4y2z.
(3)原式= x6y3·(-4xy)
=- x7y4.
八年级数学·上 新课标 [人]
14.1.4 整式的乘法(2)
第十四章 整式的乘法与因式分解
为了扩大绿地面积,要把街心花园的一块长p m,宽b m的长方形绿地,向两边分别加宽a m和c m,你能用几种方法表示扩大后的绿地面积 不同的表示方法之间有什么关系 如何从数学的角度认识不同的表示方法之间的关系
一、问题探究
(1)扩大后绿地的长和宽分别是多少
长为 m;宽为 m.
(2)根据长方形的面积=长×宽,你能得到的式子是: ①.
(3)利用分割法,可以把扩大后的面积看成几部分面积的和.
如上图,面积可以表示为 ②.
(4)这三部分的面积可以怎么表示
(5)①和②都表示扩大后绿地的面积,它们是什么关系呢
由于①和②都表示同一个量,所以这两个式子相等,即p(a+b+c)=pa+pb+pc.
用p乘以括号里的每一项,再把所得的积相加.
(6)对于这个等式,同学们想一想:你能用乘法分配律说明这个等式吗
p和a+b+c分别是什么样的式子
p是单项式,a+b+c是多项式,这个乘法是单项式与多项式的乘法,请同学们试着总结一下单项式与多项式相乘的法则.
一般地,单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
因为代数式中的字母都表示数,所以单项式可以看做是一个数,多项式可以看做是若干个数的和.因此,单项式与多项式相乘,可以利用乘法分配律,用单项式去乘多项式的每一项,从而转化为单项式的乘法,最后再把所得的积相加即可.
(1)在运用单项式与多项式相乘
的法则时要注意各项的符号问题,
且此法则是由乘法分配律推导出
来的,所以单项式与多项式相乘可
按乘法分配律进行计算.
(2)等式的左边是积,等式的右边
是和.
(3)单项式与多项式相乘所得的
结果是一个多项式,它的项数等
于原来多项式的项数.
计算:
(1)(-4x2)(3x+1);
解:
(1)原式=(-4x2)·3x+(-4x2)×1
=(-4×3)(x2·x)+(-4x2)
=-12x3-4x2.
(2)原式=
解: 原式=-x 3y+3x 2y 2-10x 3y+10x 2y 2
=-11x 3y+13x 2y 2.
化简:
解方程:8x (5-x )=19-2x (4x-3).
40x-8x2=19-8x2+6x
40x-6x=19
34x=19
解:8x(5-x)=19-2x(4x-3)
1.单项式乘以多项式的
法则:
一般地,单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
小结
2.运用单项式乘以多项式的法
则时,应注意以下几个问题:
(1)单项式与多项式相乘实质上是转化为单项式乘以单项式.
(2)用单项式去乘多项式中的每一项时,不能漏乘.
(3)注意确定积的符号.
(4)多项式中有几项,结果就是几项.
(5)多项式中的每一项都包括它前面
的符号.
C
1.计算2x(3x 2+1),正确的结果是 ( )
A.5x 3+2x B.6x 3+1
C.6x 3+2x D.6x 2+2x
A
2.-5x·(2x 2-x+3)的计算结果为 ( )
A.-10x 3+5x 2-15x
B.-10x 3-5x 2+15x
C.10x 3-5x 2-15x
D.-10x 3+5x 2-3
3.计算(-2a 3+3a 2-4a)(-5a 5)等于 ( )
A.10a 15-15a 10+20a 5
B.-7a 8-2a 7-9a 6
C.10a 8+15a 7-20a 6
D.10a 8-15a 7+20a 6
D
4.计算
八年级数学·上 新课标 [人]
14.1.4 整式的乘法(3)
第十四章 整式的乘法与因式分解
单项式乘多项式运算法则是什么?
整式的乘法实际上就是:
单项式×单项式
单项式×多项式
多项式×多项式
如图所示,为了扩大街心花园的绿地面积,把一块原长a m、宽p m的长方形绿地,加长了b m,加宽了q m.你能用几种方法求出扩大后的绿地面积
你能根据题意抽象出图形吗?
一、法则的推导
1.长方形的长是 ,宽是 .
根据长方形的面积公式面积可表示为:
。
a+b
p+q
(a+b)·(p+q)
2.如果把长方形分成两部分,一个一边是a 的长方形和一个一边是b 的长方形,则面积可表示为 .
a(p+q)+b(p+q)
3.如果分成四部分,则面积为 .如下图所示.
ap+aq+bp+bq
4.观察以上几个算式,你从计算过程中发现了什么
(a+b)(p+q)=a(p+q)+b(p+q)
=ap+aq+bp+bq.
多项式乘以多项式
5.想一想:上面的乘法属于哪一种运算
(a+b)+(p+q)=ap+aq+bp+bq.
上面的等式提供了多项式与多项式相乘的方法.
总体上看,(a+b)(p+q)的结果可以看成由a+b 的每一项乘p+q 的每一项,再把所得的积相加而得到的,即:
一般地,多项式与多项式相乘,先用一个多项式的每一项去乘另一个多项式的每一项,再把所得的积相加.
整式的乘法中我们学习了三个运算法则,它们都是由乘法的运算律推理出来的,为方便记忆,特归纳如下:
总结
乘法
在这三个法则中,单项式乘单项式的法则是基础、是关键.
解: (1)(3x+1)(x+2)
= (3x )· x+(3x )×2+1·x+1×2
= 3x2+6x+x+2
= 3x2+7x+2.
例6:计算:
(1)(3x+1)(x+2); (2)(x- 8y )(x-y );
(3)(x+y )(x 2 -xy+y 2).
(2)(x-8y )(x-y )
=x 2-xy-8xy+8y 2
=x 2-9xy+8y 2 .
(3)(x+y)(x 2 -xy+y 2)
=x 3-x 2y+xy 2+x 2y-xy 2 +y 3
=x 3 +y 3.
例(x 2-3x+n)(x 2+mx+8)的结果中不含x 2和x 3的项,求m,n 的值.
∵不含x 2和x 3的项,
∴m-3=0,8-3m+n=0.
∴m=3,n=1.
解: (x 2-3x+n)(x 2+mx+8)=x 4+mx 3+8x 2-3x 3-3mx 2-24x+nx 2+nmx+8n
=x 4+(m-3)x 3+(8-3m+n)x 2-(24-mn)x+8n,
1.多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
小结
2.运用法则时注意以下两点:
(1)相乘时,按一定顺序进行,必须做
到不重不漏.
(2)多项式与多项式相乘,仍得多项式,
在合并同类项之前,积的项数应等于原
多项式的项数之积.
D
1.下列各式中,计算结果是x 2+7x-18的是 ( )
A.(x-1)(x+18) B.(x+2)(x+9)
C.(x-3)(x+6) D.(x-2)(x+9)
A
2.(x-1)(2x+3)的计算结果是 ( )
A.2x 2+x-3 B.2x 2-x-3
C.2x 2-x+3 D.x 2-2x-3
3.若(x-2)(x+a)=x 2+bx-2,则a+b等于 ( )
A.-1 B.0
C.1 D.2
B
4.计算.
(1)(3x+2)(2x-1);
(2)(2x-8y )(x-3y );
(3)(2m-n)(3m- 4n);
(4)(2x 2-1)(2x-3);
(5)(2a-3)2;
(6)(3x-2)(3x+2)-6(x 2+x-1).
(6)原式=(3x)2+6x-6x-4-6x 2-6x+6
=3x 2-6x+2.
解: (1)原式=3x·2x-3x+2×2x-2=6x 2+x-2.
(2)原式=2x·x-2x·3y-8y·x+8y·3y
=2x 2-14xy+24y 2.
(3)原式=2m·3m-2m·4n-3m·n+n·4n
=6m2-11mn+4n 2.
(4)原式=2x 2·2x+2x 2×(-3)-2x+3
=4x 3-6x 2-2x+3.
(5)原式=(2a-3)(2a-3)
=(2a)2-6a-6a+9=4a 2-12a+9.
八年级数学·上 新课标 [人]
14.1.4 整式的乘法(4)
第十四章 整式的乘法与因式分解
一、同底数幂的除法
2.填空:
(1)( )·28=216;
(2)( )·53=55;
(3)( )·105=107;
(4)( )·a3=a6.
1.计算:
(3)102×105; (4)a3·a3.
(1)28×28;
(2)52×53;
28
52
102
a3
(1)216÷28=( );
(2)55÷53=( );
(3)107÷105=( );
(4)a 6÷a3=( ).
从上述运算能否发现商与除数、被除数有什么关系
同底数幂相除,底数不变,指数相减.
用公式表示为am÷an=am-n(a≠0,m,n 都是正整数,且m≥n).
这里的a为什么不等于0
现在我们学的指数都是大于或等于零的数,所以m≥n.
(因为0的任何次幂都是0,而0不能作除数,所以a≠0)
当m=n时,am÷an=a0=1.这样我们就得到了a0=1(a≠0),这就是说,任何不等于0的数的0次幂都等于1.
同底数幂的除法的关键在
于底数,底数一定相同,并且
二者是相除关系,这样指数才
能相减,否则不能运用此
法则.
同底数幂的除法可以从
加与减、乘与除互为逆运算
的角度来理解,在运算上常见
的错误有:(1)指数运算混乱;
(2)底数确定不对;(3)系数计
算错误;(4)运算顺序不对.
木星的质量约是1.90×1024吨,地球的质量约是5.98×1021吨.你知道木星的质量约为地球质量的多少倍吗
二、单项式除以单项式
与多项式除以单项式
这是除法运算,木星的质量约为地球质量的(1.90×1024)÷(5.98×1021)倍.
(1)计算(1.90×1024)÷(5.98×1021).
(3)你能根据(2)说说单项式除以单项
式的运算法则吗
(2)你能利用(1)中的方法计算下列各式吗
8a 3÷2a ; 6x 3y÷3xy ; 12a 3b 2x 3÷3ab 2.
1.从乘法与除法互为逆运算的角度去考虑.
(1)我们可以想象5.98×1021·( )
=1.90×1024.根据单项式与单项式相乘的运算法则:单项式与单项式相乘,是把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变作为积的因式.
所求单项式的系数乘
以5.98等于1.90,所以所求单项式系数为1.90÷5.98≈0.318,所求单项式的幂值部
分应包含1024÷1021即103,由此可知5.98×1021·(0.318×103) ≈1.90×1024.
所以(1.90×1024)÷(5.98×1021)
≈0.318×103;
(2)可以想象2a·( )=8a3,根据单项式与单项式相乘的运算法则,可以考虑:8÷2=4,a3÷a=a2,即2a·(4a2)=8a3.所以8a3÷2a=4a2.
同样的道理可以想象
3xy·( )=6x3y; 3ab2·( ) =12a3 b2x3.考虑到6÷3=2,x3÷x=x2,y÷y=1;12÷3=4,a3÷a=a2,b2÷b2 =1.所以得3xy·(2x2)=6x3y;
3ab2·(4a2·x3)=12a3 b2·x3.所以
6x3 y÷3xy=2x2;12a3b2x3÷3ab2 =4a2x3.
2.还可以从除法的意义去考虑.
(1)(1.90×1024)÷(5.98×1021)=
=×≈0.318×103;
(2)8a3÷2a==·=4a2;
6x3y÷3xy==··=2x2;
12a3b2x3÷3ab2==···x3=4a2x3.
总结
(1)都是单项式除以单项式;
(2)运算的结果都是把系数、同底数幂分别相除后作为商的因式;对于只在一个被除式中含有的字母,则连同它的指数一起作为商的一个因式;
(3)单项式相除是在同底数幂的除法的基础上进行的.
(1)(am+bm)÷m ;
(2)(a 2 +ab)÷a ;
(3)(4x 2y+2xy 2)÷2xy .
再探新知计算下列各式:
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.用公式表示为(am+bm)÷m=am÷m+bm÷m=a+b.
多项式除以单项式,也可以通过“约分”导出运算性质,不过要明确约分的依据,该依据是分数的基本性质,即分子、分母同时除以一个不等于零的数,分数的值不变.
例8 计算:
(1) 28x4y2÷7x3y;
(2)-5a5b3c÷15a4b.
解:(1) 28x4y2÷7x3y
(2)-5a5b3c÷15a4b
1.同底数幂的除法.
同底数幂的除法,底数不变,指数相减.
任何不等于零的数的零次幂都等于1.
在应用同底数幂的除法时,要注意与同底数幂乘法的区别,底数可以是单项式也可以是多项式;当三个或三个以上的同底数幂相除时,同样可以适用这一性
质.
小结
2.单项式除以单项式.
关注:(1)从法则可以看出,单项式
除以单项式分为三个步骤:一是系数相除;二是同底数幂相除;三是对于被除式中含有的字母直接作为商的一个因式.
(2)计算的结果是否正确可以利用单项式的乘法验证.
3.多项式除以单项式.
说明:多项式除以单项式的实质就是转化为单项式除以单项式.
多项式除以单项式的结果仍然是多项式.
C
1.计算-12a 6÷(3a 2)的结果是 ( )
A.- 4a 3 B.- 4a 8 C.- 4a 4 D.-a 4
B
2.计算(a 3b)2÷(ab)2的结果是 ( )
A.a 3 B.a 4
C.a 3b D.a 4b
3.地球赤道长约为4×104千米,我国最长的河流——长江全长约为6.3×103千米,赤道长约等于长江长的 ( )
A.7倍 B.6倍 C.5倍 D.4倍
B
4.计算下列各题.(1)(3a2b)3·(-2ab4)2÷(6a5b3);
解:(1)(3a2b)3.(2ab4)2(6a5b3)
=27a6b3·4a2b8÷6a5b3
=108a8b11÷6a5b3=18a3b8.
=3a2b+2ab2-1.
谢 谢 观 看
