直线的倾斜角与斜率
图片预览




文档简介
课件15张PPT。直线的倾斜角与斜率叶银川近代科学的始祖--笛卡儿业余数学王子--费马解析几何的创立在数学史上具有
划时代的意义,是数学发展史上
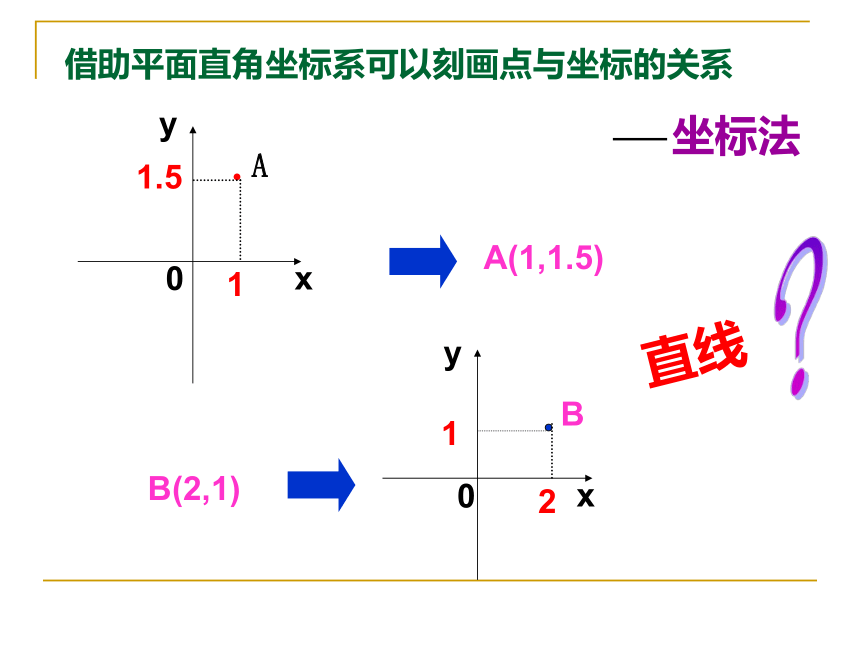
的一个里程碑。借助平面直角坐标系可以刻画点与坐标的关系A(1,1.5)B(2,1)直线?问题:1、经过原点的直线有多少条?彼此间的位置关
系如何?2、向上方向与x轴正方向所成的角为300的直线有多少
条?彼此间的位置关系?3、经过原点并且向上方向与x轴正方向所成的角为300
的直线有多少条?4、在平面直角坐标系中,怎样确定一条直线?
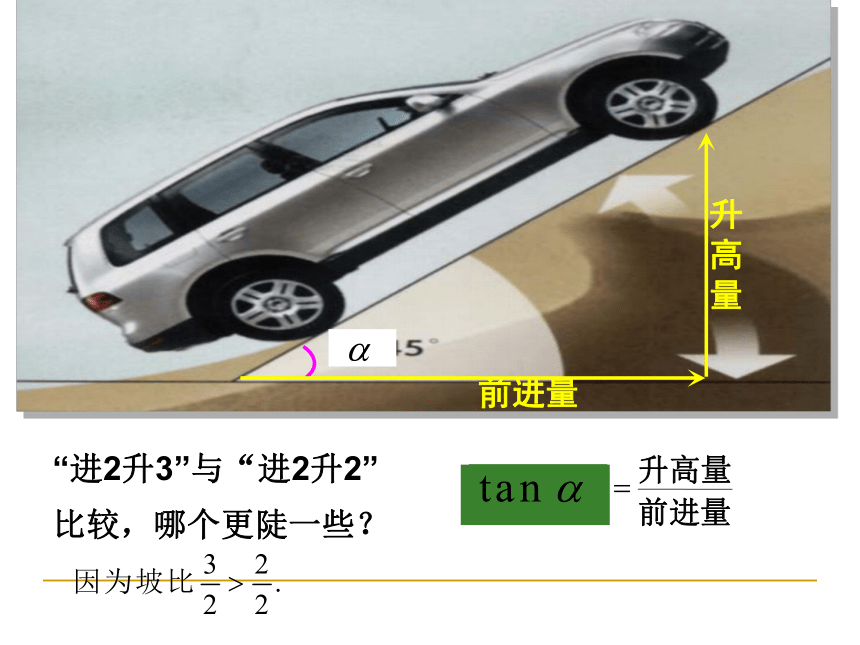
结论:确定直线位置的几何条件是:已知直线上的一个点和这条直线的方向(即直线与x轴正方向所成的角)1)倾斜角的取值范围:2)倾斜角的作用——刻画直线相对x轴的倾斜程度思考:除了倾斜角外,是否还有其它刻画直线倾斜程度的量?倾斜角:直线 与 轴正方向所成的角,叫做直线的倾斜角.常用 表示.00≤ <1800“进2升3”与“进2升2”
比较,哪个更陡一些? 一条直线的倾斜角 的正切值叫做这条直线的斜率. 1)倾斜角是 900的直线有斜率吗?直线的斜率的定义:2)斜率与倾斜角有何联系?1、已知下列直线的倾斜角,求直线的斜率:2、已知下列直线的斜率,求直线的倾斜角:结论:反之亦成立两点的斜率公式Q练一练:P95 2 例1 如图 ,已知 ,求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.解:直线AB的斜率直线BC的斜率直线CA的斜率 由 及 知,直线AB 与CA的倾斜角均为锐角;由 知,直线BC的倾斜角为钝角.典型例题 例2 在平面直角坐标系中,画出经过原点
且斜率为1直线l1. 解:设 A ( x 0,y0)是 直线l2上的一点 ,根据斜率公式有: 设 x0 =1,则 y0=-3 ,于是 A 点的坐标是(1,-3) .典型例题斜率 k=2 ?xy所以,过原点及(1,-3) 的直线即为l2 .经过原点且斜率为-3的直线 l2怎么画?典型例题 例3 已知A(-3,-5),B(1,3),C(5,11)三点,
证明:这三点在同一条直线上.解:直线AB的斜率直线BC的斜率已知直线的斜率k=3,A(2,1),B(1,x),C(y,-2)是这条直线上的三个点,则x= ,y= .-21课堂小结1、倾斜角和斜率的概念:
2、求直线斜率的方法:
3、数学思想方法: a)是刻画直线倾斜程度的两个量。
c)倾斜角取值范围[0,π)
b)任何一条直线都有唯一的倾斜角,但不一定有斜率 数形结合思想。
以数解形-----解析几何作业P98 1、2、3、4
划时代的意义,是数学发展史上
的一个里程碑。借助平面直角坐标系可以刻画点与坐标的关系A(1,1.5)B(2,1)直线?问题:1、经过原点的直线有多少条?彼此间的位置关
系如何?2、向上方向与x轴正方向所成的角为300的直线有多少
条?彼此间的位置关系?3、经过原点并且向上方向与x轴正方向所成的角为300
的直线有多少条?4、在平面直角坐标系中,怎样确定一条直线?
结论:确定直线位置的几何条件是:已知直线上的一个点和这条直线的方向(即直线与x轴正方向所成的角)1)倾斜角的取值范围:2)倾斜角的作用——刻画直线相对x轴的倾斜程度思考:除了倾斜角外,是否还有其它刻画直线倾斜程度的量?倾斜角:直线 与 轴正方向所成的角,叫做直线的倾斜角.常用 表示.00≤ <1800“进2升3”与“进2升2”
比较,哪个更陡一些? 一条直线的倾斜角 的正切值叫做这条直线的斜率. 1)倾斜角是 900的直线有斜率吗?直线的斜率的定义:2)斜率与倾斜角有何联系?1、已知下列直线的倾斜角,求直线的斜率:2、已知下列直线的斜率,求直线的倾斜角:结论:反之亦成立两点的斜率公式Q练一练:P95 2 例1 如图 ,已知 ,求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.解:直线AB的斜率直线BC的斜率直线CA的斜率 由 及 知,直线AB 与CA的倾斜角均为锐角;由 知,直线BC的倾斜角为钝角.典型例题 例2 在平面直角坐标系中,画出经过原点
且斜率为1直线l1. 解:设 A ( x 0,y0)是 直线l2上的一点 ,根据斜率公式有: 设 x0 =1,则 y0=-3 ,于是 A 点的坐标是(1,-3) .典型例题斜率 k=2 ?xy所以,过原点及(1,-3) 的直线即为l2 .经过原点且斜率为-3的直线 l2怎么画?典型例题 例3 已知A(-3,-5),B(1,3),C(5,11)三点,
证明:这三点在同一条直线上.解:直线AB的斜率直线BC的斜率已知直线的斜率k=3,A(2,1),B(1,x),C(y,-2)是这条直线上的三个点,则x= ,y= .-21课堂小结1、倾斜角和斜率的概念:
2、求直线斜率的方法:
3、数学思想方法: a)是刻画直线倾斜程度的两个量。
c)倾斜角取值范围[0,π)
b)任何一条直线都有唯一的倾斜角,但不一定有斜率 数形结合思想。
以数解形-----解析几何作业P98 1、2、3、4
