24.1.2 垂直于弦的直径 课件 2023-2024学年人教版九年级数学上册(16张PPT)
文档属性
| 名称 | 24.1.2 垂直于弦的直径 课件 2023-2024学年人教版九年级数学上册(16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 20:48:29 | ||
图片预览




文档简介
(共16张PPT)
第二十四章 圆
24.1.2 垂直于弦的直径
1.理解圆的轴对称性,掌握垂径定理及其推论.
2.能运用垂径定理及其推论解决相关问题.
任务一:理解圆的轴对称性,掌握垂径定理及其推论.
活动:小组讨论解决下列问题.
(1) 用纸剪一个圆,沿着圆的任意一条直径对折,重复几次,你发现了什么?
由此你能得到什么结论?
圆是轴对称图形,任何一条直径所在直线都是圆的对称轴.
如何证明该结论呢?
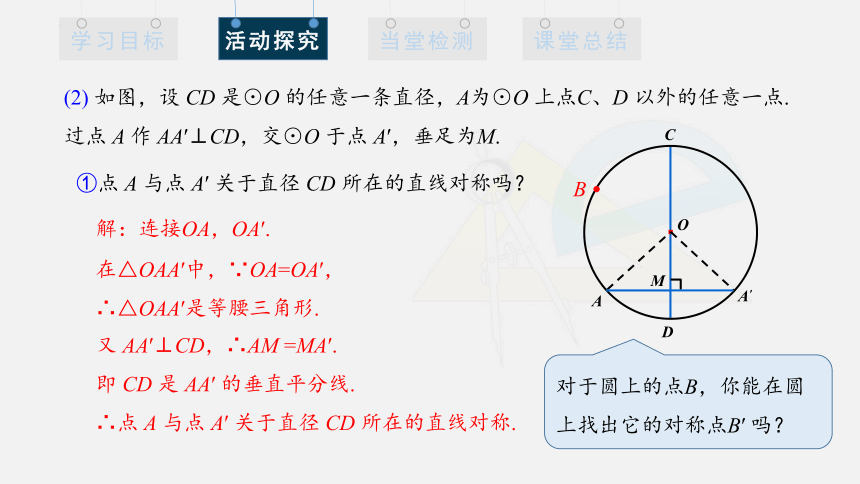
①点 A 与点 A′ 关于直径 CD 所在的直线对称吗?
·
O
A
A'
C
D
M
(2) 如图,设 CD 是⊙O 的任意一条直径,A为⊙O 上点C、D 以外的任意一点. 过点 A 作 AA′⊥CD,交⊙O 于点 A′,垂足为M.
在△OAA′中,∵OA=OA′,
∴△OAA′是等腰三角形.
又 AA′⊥CD,∴AM =MA′.
即 CD 是 AA′ 的垂直平分线.
∴点 A 与点 A′ 关于直径 CD 所在的直线对称.
B
对于圆上的点B,你能在圆上找出它的对称点B′ 吗?
解:连接OA,OA′.
方法提炼:要证明圆是轴对称图形,只需证明圆上任意一点关于直径所在直线(对称轴)的对称点也在圆上.
·
O
A
A'
C
D
M
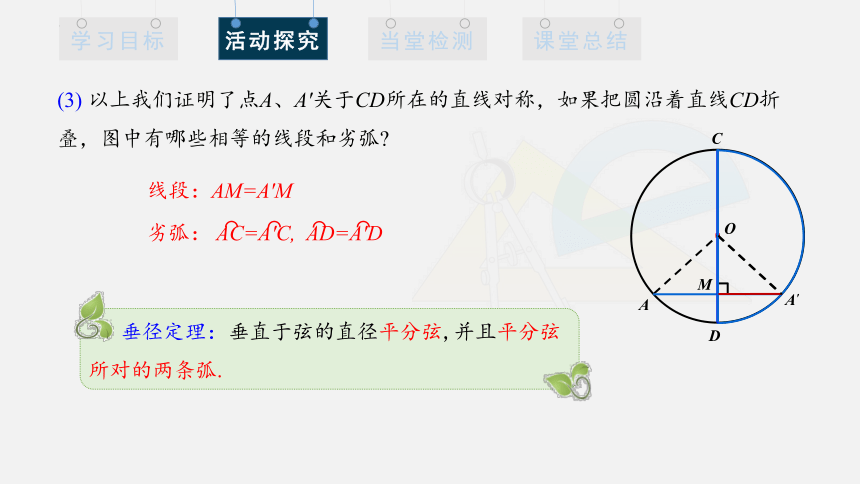
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
(3) 以上我们证明了点A、A′关于CD所在的直线对称,如果把圆沿着直线CD折叠,图中有哪些相等的线段和劣弧
·
O
A
A'
C
D
M
线段:AM=A′M
劣弧: AC=A′C, AD=A′D
⌒
⌒
⌒
⌒
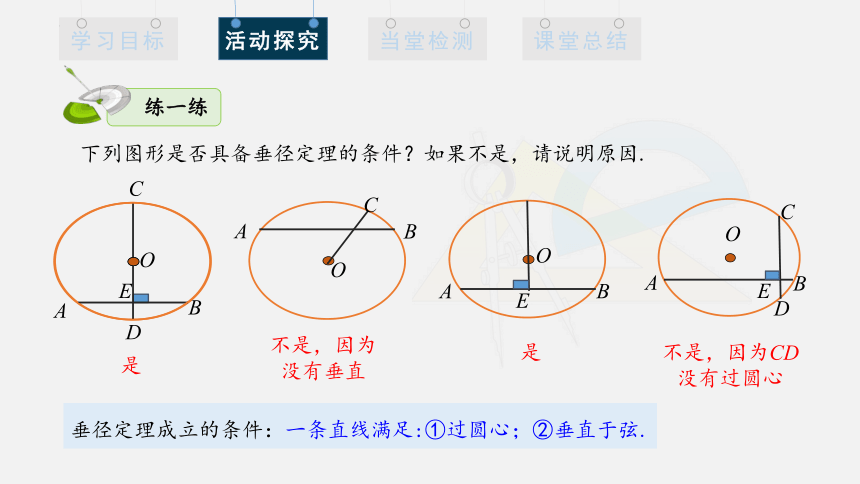
练一练
下列图形是否具备垂径定理的条件?如果不是,请说明原因.
A
B
O
C
D
E
O
A
B
C
A
B
O
E
A
B
D
C
O
E
是
不是,因为没有垂直
是
不是,因为CD没有过圆心
垂径定理成立的条件:一条直线满足:①过圆心;②垂直于弦.
M
思考:反过来,经过弦AA′ (不是直径)中点 M 的直径,垂直于AA′ 且平分AA′ 所对的两条弧吗?请说明原因.
·
O
A
A'
C
D
⌒
⌒
⌒
⌒
由垂径定理可得:AC=A′C, AD=A′D.
解:连接AO,A′O,则AO=A′O.
又 AM=A′M,∴△AOM≌△A′OM (SSS).
∴∠AMO=∠A′MO=90°.
∴CD⊥AA′.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
垂径定理的推论:
“不是直径”这个条件能去掉吗?
不能,圆的任意两条直径都是互相平分的,却不一定互相垂直.
·
O
A
B
C
D
M
·
O
A
A'
C
D
任务二:运用垂径定理及其推论解决相关问题.
活动:赵州桥(如图)是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代人民勤劳与智慧的结晶. 它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37 m,拱高(弧的中点到弦的距离)为7.23 m. 求赵州桥主桥拱的半径(结果保留小数点后一位).
(1) 你能找出赵州桥主桥拱的半径吗?根据赵州桥的实物图画出几何图形,并求出赵州桥主桥拱的半径.
解:如图,用 表示主桥拱,设 所在圆的圆心为 O,半径为 R.
R
AB
(
经过圆心 O 作弦 AB 的垂线 OC,垂足为 D,与 交于点 C. 根据垂径定理,D 是AB 的中点,C是 的中点,CD 就是拱高.
AB
(
AB
(
AB
(
∴ AB=37m,CD=7.23m.
R
解得:R ≈ 27.3.
在 Rt△OAD中,由勾股定理,得:
即:R2 = 18.52 + (R – 7.23)2,
因此,赵州桥的主桥拱半径约为27.3 m.
OA2 = AD2 + OD2
OD = OC – CD = R – 7.23
活动小结
在圆中,解决有关弦的问题时,只需从圆心作一条与弦垂直的线段,如图:
·
O
A
B
r
d
a
(r:圆的半径 ,d:圆心到弦的距离 ,a:弦长)
1.如图,已知☉O的直径AB⊥CD于点E,则下列结论错误的是( )
A. CE=DE B.AE=OE
C. BC=BD D.△OCE≌△ODE.
B
(
(
2.某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16 m,半径OA=10 m,
求蔬菜大棚的高度CD.
解:
在Rt△OAD中,由勾股定理,得 OA2=AD2+OD2,
∵AB=16 m,
由垂径定理,得AD=8m.
求得OD=6m.
∴CD=OC-OD=4m.
∵OC=OA=10m,
针对本节课的关键词“垂径定理”,你能说说学到了哪些知识吗?
垂径定理
内容
推论
辅助线
垂直于弦的直径平分弦,
并且平分弦所对的两条弧.
两条辅助线:
连半径,作弦心距.
构造Rt△,利用勾股定理计算或建立方程.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
第二十四章 圆
24.1.2 垂直于弦的直径
1.理解圆的轴对称性,掌握垂径定理及其推论.
2.能运用垂径定理及其推论解决相关问题.
任务一:理解圆的轴对称性,掌握垂径定理及其推论.
活动:小组讨论解决下列问题.
(1) 用纸剪一个圆,沿着圆的任意一条直径对折,重复几次,你发现了什么?
由此你能得到什么结论?
圆是轴对称图形,任何一条直径所在直线都是圆的对称轴.
如何证明该结论呢?
①点 A 与点 A′ 关于直径 CD 所在的直线对称吗?
·
O
A
A'
C
D
M
(2) 如图,设 CD 是⊙O 的任意一条直径,A为⊙O 上点C、D 以外的任意一点. 过点 A 作 AA′⊥CD,交⊙O 于点 A′,垂足为M.
在△OAA′中,∵OA=OA′,
∴△OAA′是等腰三角形.
又 AA′⊥CD,∴AM =MA′.
即 CD 是 AA′ 的垂直平分线.
∴点 A 与点 A′ 关于直径 CD 所在的直线对称.
B
对于圆上的点B,你能在圆上找出它的对称点B′ 吗?
解:连接OA,OA′.
方法提炼:要证明圆是轴对称图形,只需证明圆上任意一点关于直径所在直线(对称轴)的对称点也在圆上.
·
O
A
A'
C
D
M
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
(3) 以上我们证明了点A、A′关于CD所在的直线对称,如果把圆沿着直线CD折叠,图中有哪些相等的线段和劣弧
·
O
A
A'
C
D
M
线段:AM=A′M
劣弧: AC=A′C, AD=A′D
⌒
⌒
⌒
⌒
练一练
下列图形是否具备垂径定理的条件?如果不是,请说明原因.
A
B
O
C
D
E
O
A
B
C
A
B
O
E
A
B
D
C
O
E
是
不是,因为没有垂直
是
不是,因为CD没有过圆心
垂径定理成立的条件:一条直线满足:①过圆心;②垂直于弦.
M
思考:反过来,经过弦AA′ (不是直径)中点 M 的直径,垂直于AA′ 且平分AA′ 所对的两条弧吗?请说明原因.
·
O
A
A'
C
D
⌒
⌒
⌒
⌒
由垂径定理可得:AC=A′C, AD=A′D.
解:连接AO,A′O,则AO=A′O.
又 AM=A′M,∴△AOM≌△A′OM (SSS).
∴∠AMO=∠A′MO=90°.
∴CD⊥AA′.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
垂径定理的推论:
“不是直径”这个条件能去掉吗?
不能,圆的任意两条直径都是互相平分的,却不一定互相垂直.
·
O
A
B
C
D
M
·
O
A
A'
C
D
任务二:运用垂径定理及其推论解决相关问题.
活动:赵州桥(如图)是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代人民勤劳与智慧的结晶. 它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37 m,拱高(弧的中点到弦的距离)为7.23 m. 求赵州桥主桥拱的半径(结果保留小数点后一位).
(1) 你能找出赵州桥主桥拱的半径吗?根据赵州桥的实物图画出几何图形,并求出赵州桥主桥拱的半径.
解:如图,用 表示主桥拱,设 所在圆的圆心为 O,半径为 R.
R
AB
(
经过圆心 O 作弦 AB 的垂线 OC,垂足为 D,与 交于点 C. 根据垂径定理,D 是AB 的中点,C是 的中点,CD 就是拱高.
AB
(
AB
(
AB
(
∴ AB=37m,CD=7.23m.
R
解得:R ≈ 27.3.
在 Rt△OAD中,由勾股定理,得:
即:R2 = 18.52 + (R – 7.23)2,
因此,赵州桥的主桥拱半径约为27.3 m.
OA2 = AD2 + OD2
OD = OC – CD = R – 7.23
活动小结
在圆中,解决有关弦的问题时,只需从圆心作一条与弦垂直的线段,如图:
·
O
A
B
r
d
a
(r:圆的半径 ,d:圆心到弦的距离 ,a:弦长)
1.如图,已知☉O的直径AB⊥CD于点E,则下列结论错误的是( )
A. CE=DE B.AE=OE
C. BC=BD D.△OCE≌△ODE.
B
(
(
2.某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16 m,半径OA=10 m,
求蔬菜大棚的高度CD.
解:
在Rt△OAD中,由勾股定理,得 OA2=AD2+OD2,
∵AB=16 m,
由垂径定理,得AD=8m.
求得OD=6m.
∴CD=OC-OD=4m.
∵OC=OA=10m,
针对本节课的关键词“垂径定理”,你能说说学到了哪些知识吗?
垂径定理
内容
推论
辅助线
垂直于弦的直径平分弦,
并且平分弦所对的两条弧.
两条辅助线:
连半径,作弦心距.
构造Rt△,利用勾股定理计算或建立方程.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
同课章节目录
