25.3 用频率估计概率 课件 14张PPT 2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 25.3 用频率估计概率 课件 14张PPT 2023—2024学年人教版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 21:24:23 | ||
图片预览






文档简介
(共14张PPT)
第二十五章 概率初步
25.3 用频率估计概率
问题导入
抛掷一枚质地均匀的硬币,“正面向上”和“反面向上”发生的可能性相等,这两个随机事件发生的概率都是0.5,这个概率能否利用试验的方法——通过统计很多掷硬币的结果来得到呢?
1.掌握用频率估计概率的方法,并能解决实际问题.
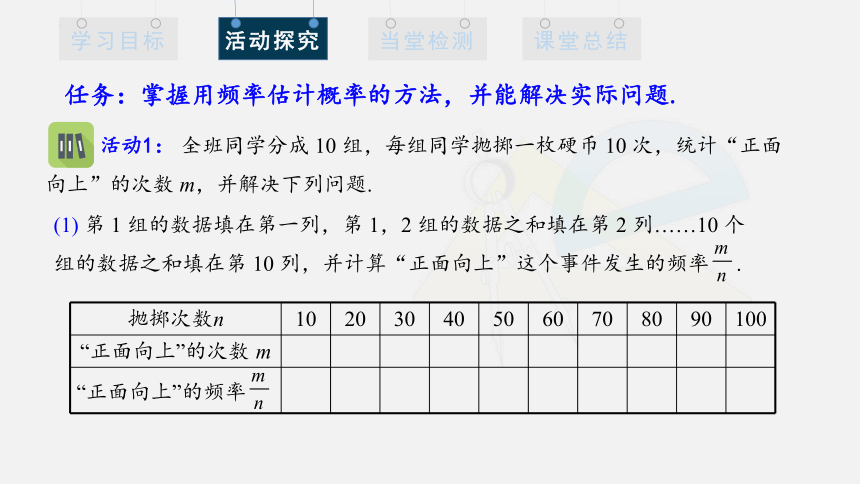
任务:掌握用频率估计概率的方法,并能解决实际问题.
活动1: 全班同学分成 10 组,每组同学抛掷一枚硬币 10 次,统计“正面向上”的次数 m,并解决下列问题.
抛掷次数n 10 20 30 40 50 60 70 80 90 100
“正面向上”的次数 m
“正面向上”的频率
(1) 第 1 组的数据填在第一列,第 1,2 组的数据之和填在第 2 列……10 个组的数据之和填在第 10 列,并计算“正面向上”这个事件发生的频率 .
10 20 30 40 50 60 70 80 90 100 抛掷次数 n
“正面向上”的频率
1.0
0.5
O
(2) 根据上表中的数据,在下图中标注出对应的点,“正面向上”的频率有什么规律?
随着抛掷硬币次数的增加,硬币“正面朝上”的频率会在0.5左右摆动,并且摆动幅度越来越小.
(3) 阅读课本第143页的表 25-4,画出其“正面向上”频率的变化趋势图. 随着抛掷次数的增加,“正面向上”的频率的变化趋势是什么?
0.5
2048
4040
10000
12000
24000
0
“正面向上”的频率
抛掷次数 n
随着试验次数的增加,“正面向上”的频率稳定于0.5.
对一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总是在一个固定数的附近摆动,显示出一定的稳定性.
一般地,在大量重复试验中,如果事件A发生的频率 稳定在某个常数 p 附近,那么这个常数 p 就叫做事件A的概率,记为P(A)=p.
活动小结
概率与频率的区别与联系:
名称 频率 概率
区别 实验值或统计值 理论值
具有随机性 具有唯一性
近似反映事件发生的可能性大小 精确反映事件发生的可能性大小
联系 当试验次数很大时,事件发生的频率稳定在相应概率附近.
练一练
在一定条件下,掷一枚图钉,如何计算针尖朝上的概率?
针尖朝上和针尖朝下并不是等可能事件,故不能直接使用列举法确切的计算出随机事件的概率. 但可通过大量重复试验估计出它的概率.
用频率估计概率,不受“各种结果出现的可能性相等”的条件限制,可求概率的随机事件的范围更大.
活动2:某林业部门要考查某种幼树在一定条件的移植的成活率,小组讨论解决下列问题.
(1) 可以用列举法求出该幼树移植的成活率吗?
(2) 设计一个具体做法求这批幼树成活的概率.
答:(1) 不能,该幼树移植“成活”与“不成活”两种结果可能性是否相等未知.
(2) 在同样条件下,对这种幼树进行大量移植,并统计成活情况,计算成活的频率. 随着 n 越来越大,频率 会越来越稳定,就可以把频率作为成活率的估计值.
移植总数 n 成活率 m 成活的频率
10 8 0.80
50 47
270 235 0.871
400 369
750 662
1500 1335 0.890
3500 3203 0.915
7000 6335
9000 8073
14000 12628 0.902
0.94
0.923
0.883
0.905
0.897
(3) 下表是一张模拟的统计表,补全表中的空缺(结果保留小数点后三位).
思考:随着移植数的增加,幼树移植成活的频率有什么趋势?据此可估计幼树移植成活的概率为多少?
答:随着移植数的增加,幼树移植成活的频率越来越稳定. 于是可估计幼树移植成活的概率是 0.9.
1. 在大量重复实验中,关于随机事件发生的概率,下列说法正确的是( )
A. 频率就是概率
B. 频率与实验次数无关
C. 概率是随机的,与频率无关
D. 随着实验次数的增加,频率一般会越来越接近概率
D
2.教练记录一名主力前锋练习罚篮的结果如下:
练习次数 30 60 90 150 200 300 400 500
罚中次数 27 45 78 118 161 239 322 401
罚中频率
0.900
0.750
0.867
0.787
0.805
0.797
0.805
0.802
随着练习次数的增加,罚中频率稳定在0.8左右,所以估计他这次能罚中的概率约为0.8.
(1)填表(精确到0.001);
(2)比赛中罚篮一次,估计这次他能罚中的概率是多少?
针对本节课的关键词“用频率估计概率”,你能说说学到了哪些知识吗?
用频率估计概率
频率和概率的关系
步骤
频率是概率的近似值,概率是频率的稳定值.
①大量重复试验;
②检验频率是否已表现出稳定性;
③频率的稳定值即为概率.
第二十五章 概率初步
25.3 用频率估计概率
问题导入
抛掷一枚质地均匀的硬币,“正面向上”和“反面向上”发生的可能性相等,这两个随机事件发生的概率都是0.5,这个概率能否利用试验的方法——通过统计很多掷硬币的结果来得到呢?
1.掌握用频率估计概率的方法,并能解决实际问题.
任务:掌握用频率估计概率的方法,并能解决实际问题.
活动1: 全班同学分成 10 组,每组同学抛掷一枚硬币 10 次,统计“正面向上”的次数 m,并解决下列问题.
抛掷次数n 10 20 30 40 50 60 70 80 90 100
“正面向上”的次数 m
“正面向上”的频率
(1) 第 1 组的数据填在第一列,第 1,2 组的数据之和填在第 2 列……10 个组的数据之和填在第 10 列,并计算“正面向上”这个事件发生的频率 .
10 20 30 40 50 60 70 80 90 100 抛掷次数 n
“正面向上”的频率
1.0
0.5
O
(2) 根据上表中的数据,在下图中标注出对应的点,“正面向上”的频率有什么规律?
随着抛掷硬币次数的增加,硬币“正面朝上”的频率会在0.5左右摆动,并且摆动幅度越来越小.
(3) 阅读课本第143页的表 25-4,画出其“正面向上”频率的变化趋势图. 随着抛掷次数的增加,“正面向上”的频率的变化趋势是什么?
0.5
2048
4040
10000
12000
24000
0
“正面向上”的频率
抛掷次数 n
随着试验次数的增加,“正面向上”的频率稳定于0.5.
对一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总是在一个固定数的附近摆动,显示出一定的稳定性.
一般地,在大量重复试验中,如果事件A发生的频率 稳定在某个常数 p 附近,那么这个常数 p 就叫做事件A的概率,记为P(A)=p.
活动小结
概率与频率的区别与联系:
名称 频率 概率
区别 实验值或统计值 理论值
具有随机性 具有唯一性
近似反映事件发生的可能性大小 精确反映事件发生的可能性大小
联系 当试验次数很大时,事件发生的频率稳定在相应概率附近.
练一练
在一定条件下,掷一枚图钉,如何计算针尖朝上的概率?
针尖朝上和针尖朝下并不是等可能事件,故不能直接使用列举法确切的计算出随机事件的概率. 但可通过大量重复试验估计出它的概率.
用频率估计概率,不受“各种结果出现的可能性相等”的条件限制,可求概率的随机事件的范围更大.
活动2:某林业部门要考查某种幼树在一定条件的移植的成活率,小组讨论解决下列问题.
(1) 可以用列举法求出该幼树移植的成活率吗?
(2) 设计一个具体做法求这批幼树成活的概率.
答:(1) 不能,该幼树移植“成活”与“不成活”两种结果可能性是否相等未知.
(2) 在同样条件下,对这种幼树进行大量移植,并统计成活情况,计算成活的频率. 随着 n 越来越大,频率 会越来越稳定,就可以把频率作为成活率的估计值.
移植总数 n 成活率 m 成活的频率
10 8 0.80
50 47
270 235 0.871
400 369
750 662
1500 1335 0.890
3500 3203 0.915
7000 6335
9000 8073
14000 12628 0.902
0.94
0.923
0.883
0.905
0.897
(3) 下表是一张模拟的统计表,补全表中的空缺(结果保留小数点后三位).
思考:随着移植数的增加,幼树移植成活的频率有什么趋势?据此可估计幼树移植成活的概率为多少?
答:随着移植数的增加,幼树移植成活的频率越来越稳定. 于是可估计幼树移植成活的概率是 0.9.
1. 在大量重复实验中,关于随机事件发生的概率,下列说法正确的是( )
A. 频率就是概率
B. 频率与实验次数无关
C. 概率是随机的,与频率无关
D. 随着实验次数的增加,频率一般会越来越接近概率
D
2.教练记录一名主力前锋练习罚篮的结果如下:
练习次数 30 60 90 150 200 300 400 500
罚中次数 27 45 78 118 161 239 322 401
罚中频率
0.900
0.750
0.867
0.787
0.805
0.797
0.805
0.802
随着练习次数的增加,罚中频率稳定在0.8左右,所以估计他这次能罚中的概率约为0.8.
(1)填表(精确到0.001);
(2)比赛中罚篮一次,估计这次他能罚中的概率是多少?
针对本节课的关键词“用频率估计概率”,你能说说学到了哪些知识吗?
用频率估计概率
频率和概率的关系
步骤
频率是概率的近似值,概率是频率的稳定值.
①大量重复试验;
②检验频率是否已表现出稳定性;
③频率的稳定值即为概率.
同课章节目录
