5.7三角函数的应用 学案+练习(含解析)
文档属性
| 名称 | 5.7三角函数的应用 学案+练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-11 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
5.7三角函数的应用
班级 姓名
学习目标
1.了解三角函数是描述周期变化的重要函数模型,并会用三角函数模型解决一些简单的实际问题.
2.实际问题抽象为三角函数模型.
学习过程
自学指导 自学检测及课堂展示
阅读教材,完成右边的内容 知识点 函数y=Asin(ωx+φ),A>0,ω>0中参数的物理意义【即时训练】(1)函数y=sin的周期、振幅、初相分别是( )A.3π,, B.6π,, C.3π,3,- D.6π,3,(2)函数y=3sin的频率为________,相位为________.
三角函数模型的实际应用 例1、心脏跳动时,血压在增加或减少.血压的最大值、最小值分别称为收缩压和舒张压,血压计上的读数就是收缩压和舒张压,读数120/80 mmHg为标准值.设某人的血压满足函数式p(t)=115+25sin 160πt,其中p(t)为血压(mmHg),t为时间(min),试回答下列问题:(1)求函数p(t)的周期;(2)求此人每分钟心跳的次数;(3)画出函数p(t)的草图;(4)求出此人的血压在血压计上的读数.
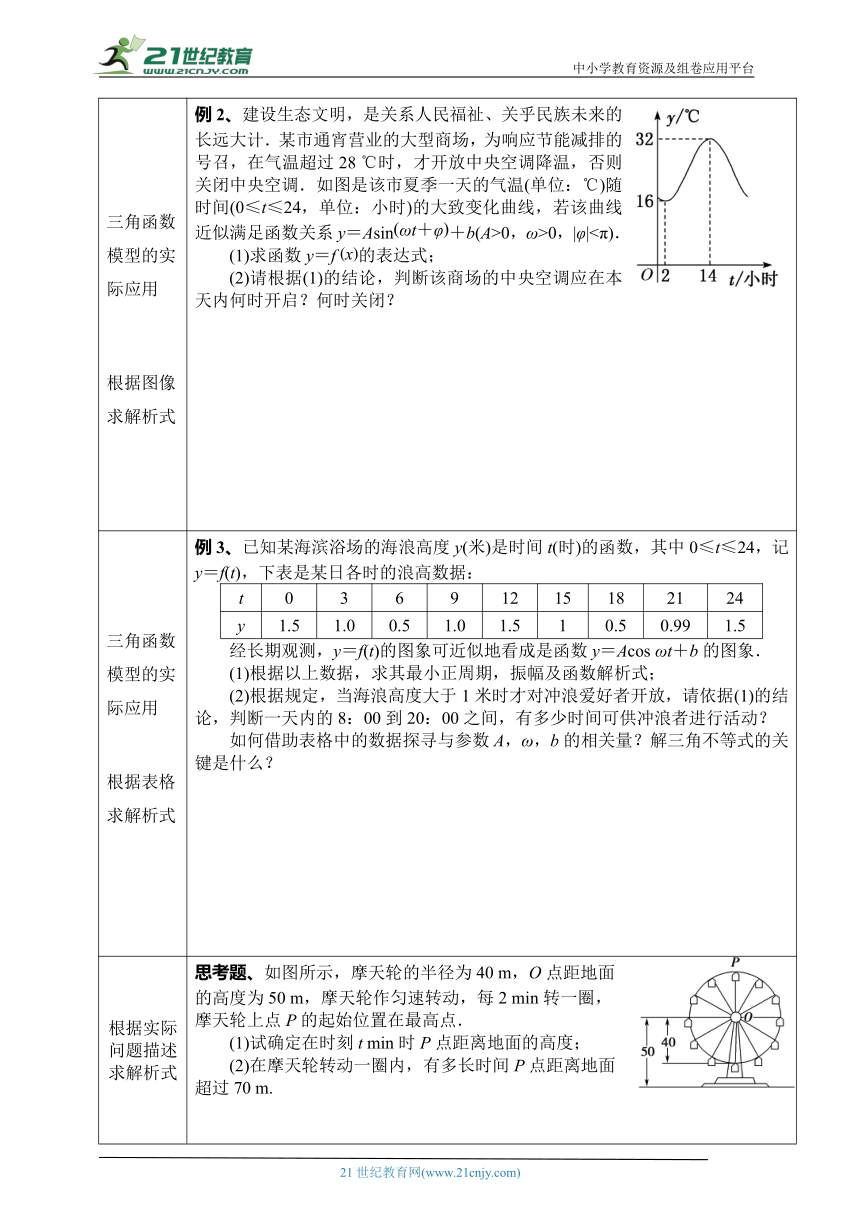
三角函数模型的实际应用根据图像求解析式 例2、建设生态文明,是关系人民福祉、关乎民族未来的长远大计.某市通宵营业的大型商场,为响应节能减排的号召,在气温超过28 ℃时,才开放中央空调降温,否则关闭中央空调.如图是该市夏季一天的气温(单位:℃)随时间(0≤t≤24,单位:小时)的大致变化曲线,若该曲线近似满足函数关系y=Asin+b(A>0,ω>0,|φ|<π).(1)求函数y=f的表达式;(2)请根据(1)的结论,判断该商场的中央空调应在本天内何时开启?何时关闭?
三角函数模型的实际应用根据表格求解析式 例3、已知某海滨浴场的海浪高度y(米)是时间t(时)的函数,其中0≤t≤24,记y=f(t),下表是某日各时的浪高数据:t03691215182124y1.51.00.51.01.510.50.991.5经长期观测,y=f(t)的图象可近似地看成是函数y=Acos ωt+b的图象.(1)根据以上数据,求其最小正周期,振幅及函数解析式;(2)根据规定,当海浪高度大于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的8:00到20:00之间,有多少时间可供冲浪者进行活动?如何借助表格中的数据探寻与参数A,ω,b的相关量?解三角不等式的关键是什么?
根据实际问题描述求解析式 思考题、如图所示,摩天轮的半径为40 m,O点距地面的高度为50 m,摩天轮作匀速转动,每2 min转一圈,摩天轮上点P的起始位置在最高点.(1)试确定在时刻t min时P点距离地面的高度;(2)在摩天轮转动一圈内,有多长时间P点距离地面超过70 m.
课后作业
一、基础训练题
1.最大值为,最小正周期为,初相为的函数表达式是( )
A.y=sin B.y=sin C.y=sin D.y=sin
2.音叉是呈“Y”形的钢质或铝合金发声器(如图1),各种音叉可因其质量和叉臂长短、粗细不同而在振动时发出不同频率的纯音.敲击某个音叉时,在一定时间内,音叉上点P离开平衡位置的位移y与时间t的函数关系为y=sin ωt.图2是该函数在一个周期内的图象,根据图中数据可确定ω的值为( )
A.200 B.400
C.200π D.400π
3.(多选题)如图所示是一个简谐运动的图象,则下列判断正确的是( )
A.该质点的运动周期为0.8 s
B.该质点的振幅为-5 cm
C.该质点在0.1 s和0.5 s时的振动速度最大 D.该质点在0.3 s和0.7 s时的位移为零
4.商场人流量被定义为每分钟通过入口的人数,五一节那天某商场的人流量满足函数F(t)=50+4sin (t≥0),则在下列时间段内人流量增加的是( )
A.[0,5] B.[5,10] C.[10,15] D.[15,20]
5.下表是某市近30年来月平均气温(℃)的数据统计表:
月份 1 2 3 4 5 6 7 8 9 10 11 12
平均温度 -5.9 -3.3 2.2 9.3 15.1 20.3 22.8 22.2 18.2 11.9 4.3 -2.4
则适合这组数据的函数模型是( )
A.y=acos B.y=acos+k(a>0,k>0)
C.y=-acos+k(a>0,k>0) D.y=acos-3
6.电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)的图象如图所示,则当t=秒时,电流强度是( )
A.-5安 B.5安 C.5安 D.10安
7.一根长l cm的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(cm)与时间t(s)的函数关系式为s=3cos,其中g是重力加速度,当小球摆动的周期是1 s时,线长l=________cm.
8.如图是弹簧振子做简谐振动的图象,横轴表示振动的时间,纵轴表示振动的位移,则这个振子振动的函数解析式是_________________.
9.一种波的波形为函数y=-sinx的图象,若其在区间[0,t]上至少有2个波峰(图象的最高点),则正整数t的最小值是________.
10.已知某地一天从4时到16时的温度变化曲线近似满足函数y=10sin +20,x∈[4,16].
(1)求该地区这一段时间内温度的最大温差;
(2)若有一种细菌在15 ℃到25 ℃之间可以生存,那么在这段时间内,该细菌能生存多长时间?
二、综合训练题
11.稳定房价是我国今年实施宏观调控的重点,国家最近出台的一系列政策已对各地的房地产市场产生了影响,温州市某房地产中介对本市一楼盘在今年的房价作了统计与预测:发现每个季度的平均单价y(每平方米的价格,单位:元)与第x季度之间近似满足:y=500sin(ωx+φ)+9 500(ω>0),已知第一、二季度平均单价如下表所示:
x 1 2 3
y 10 000 9 500 ?
则此楼盘在第三季度的平均单价大约是( )
A.10 000元 B.9 500元
C.9 000元 D.8 500元
12.如图所示,一个大风车的半径为8 m,每12 min旋转一周,最低点离地面2 m.若风车翼片从最低点按逆时针方向开始旋转,则该翼片的端点P离地面的距离h(m)与时间t(min)之间的函数关系是( )
A.h=8cost+10 B.h=-8cost+10C.h=-8sint+10 D.h=-8cost+10
13.为迎接夏季旅游旺季的到来,少林寺单独设置了一个专门安排游客住宿的客栈,寺庙的工作人员发现为游客准备的一些食物有些月份剩余不少,浪费很严重,为了控制经营成本,减少浪费,就想适时调整投入,为此他们统计每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数会发生周期性的变化,并且有以下规律:
①每年相同的月份,入住客栈的游客人数基本相同;
②入住客栈的游客人数在2月份最少,在8月份最多,相差约400人;
③2月份入住客栈的游客约为100人,随后逐月递增直到8月份达到最多.
(1)试用一个正弦型三角函数描述一年中入住客栈的游客人数与月份之间的关系;
(2)请问哪几个月份要准备400份以上的食物?
三、能力提升题
14.如图,设点A是单位圆上的一定点,动点P从点A出发在圆上按逆时针方向旋转一周,点P所旋转过的弧的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )
A B C D
15.国际油价在某一时间内呈现正弦波动规律:P=Asinωπt++60(美元)(t(天),A>0,ω>0),现采集到下列信息:最高油价80美元,当t=150(天)时达到最低油价,则ω的最小值为________.
5.7三角函数的应用
参考答案
1、【答案】D
【解析】由题意可知,周期T==,∴ω=3.∴y=sin,故选D.
2、【答案】D
【解析】由图象可得,ω>0,T=4×=,即=,则ω=400π.
3、【答案】AD
【解析】由图可知T=0.6,∴T=0.8.振幅A=5 cm,当t=0.1 s或0.5 s时,v=0.故选AD.
4、【答案】C
【解析】由2kπ-≤≤2kπ+,k∈Z,知函数F(t)的增区间为[4kπ-π,4kπ+π],k∈Z.
当k=1时,t∈[3π,5π],而[10,15] [3π,5π],故选C.
5、【答案】C
【解析】当x=1时图象处于最低点,且易知a=>0.故选C.
6、【答案】A
【解析】由图象知A=10,=-=,所以ω==100π.所以I=10sin(100πt+φ).
因为为五点作图法中的第二个点,所以100π×+φ=.所以φ=.
所以I=10sin,当t=秒时,I=-5安.
7、【答案】
【解析】由已知得=1,所以=2π,=4π2,l=.]
8、【答案】y=2sin
【解析】由题图可设y=Asin(ωt+φ),则A=2,又T=2(0.5-0.1)=0.8,
所以ω==π,所以y=2sin,将点(0.1,2)代入y=2sin中,得sin=1,
所以φ+=2kπ+,k∈Z,即φ=2kπ+,k∈Z,
令k=0,得φ=,所以y=2sin.
9、【答案】7
【解析】函数y=-sinx的周期T=4,且x=3时y=1取得最大值,因此t≥7.即正整数t的最小值是7.
10、[解] (1)由函数易知,当x=14时函数取最大值,即最高温度为30 ℃;当x=6时函数取最小值,即最低温度为10 ℃.所以,最大温差为30 ℃-10 ℃=20 ℃.
(2)令10sin+20=15,可得sin=-. 而x∈[4,16],所以x=.
令10sin+20=25,可得sin=,而x∈[4,16],
所以x=.故该细菌的存活时间为-=小时.
11、【答案】C
【解析】因为y=500sin(ωx+φ)+9 500(ω>0),所以当x=1时,500sin(ω+φ)+9 500=10 000;
当x=2时,500sin(2ω+φ)+9 500=9 500,所以ω可取,φ可取π,即y=500sin+9 500.
当x=3时,y=9 000.
12、【答案】D
【解析】依题意可设h=Asin(ωt+φ)+B(A>0,ω>0),易知T=12,A=8,B=10,所以ω==,
则h=8sin+10,当t=0时,8sin φ+10=2,得sin φ=-1,可取φ=-,
所以h=8sin+10=-8cost+10.
13、[解析] (1)设该函数为f(x)=Asin(ωx+φ)+B(A>0,ω>0,0<|φ|<π),根据条件①,
可知这个函数的周期是12;由②可知,f(2)最小,f(8)最大,且f(8)-f(2)=400,故该函数的振幅为200;
由③可知,f(x)在[2,8]上单调递增,且f(2)=100,所以f(8)=500.
根据上述分析可得,=12,故ω=,且解得
根据分析可知,当x=2时,f(x)最小,当x=8时,f(x)最大,
故sin=-1,且sin=1.又因为0<|φ|<π,故φ=-.
所以入住客栈的游客人数与月份之间的关系式为f(x)=200sin+300.
(2)由条件可知,200sin+300≥400,
化简,得sin≥ 2kπ+≤x-≤2kπ+,k∈Z,解得12k+6≤x≤12k+10,k∈Z.
因为x∈N*,且1≤x≤12,故x=6,7,8,9,10.
即只有6,7,8,9,10五个月份要准备400份以上的食物.
14、【答案】C
【解析】令AP所对圆心角为θ,由|OA|=1,得l=θ,sin=,∴d=2sin=2sin,
即d=f(l)=2sin(0≤l≤2π),它的图象为C
15、【答案】
【解析】因为Asin+60=80,sin≤1,
所以A=20,当t=150(天)时达到最低油价,即sin=-1,此时150ωπ+=2kπ-,k∈Z,因为ω>0,所以当k=1时,ω取最小值,
所以150ωπ+=π,解得ω=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
5.7三角函数的应用
班级 姓名
学习目标
1.了解三角函数是描述周期变化的重要函数模型,并会用三角函数模型解决一些简单的实际问题.
2.实际问题抽象为三角函数模型.
学习过程
自学指导 自学检测及课堂展示
阅读教材,完成右边的内容 知识点 函数y=Asin(ωx+φ),A>0,ω>0中参数的物理意义【即时训练】(1)函数y=sin的周期、振幅、初相分别是( )A.3π,, B.6π,, C.3π,3,- D.6π,3,(2)函数y=3sin的频率为________,相位为________.
三角函数模型的实际应用 例1、心脏跳动时,血压在增加或减少.血压的最大值、最小值分别称为收缩压和舒张压,血压计上的读数就是收缩压和舒张压,读数120/80 mmHg为标准值.设某人的血压满足函数式p(t)=115+25sin 160πt,其中p(t)为血压(mmHg),t为时间(min),试回答下列问题:(1)求函数p(t)的周期;(2)求此人每分钟心跳的次数;(3)画出函数p(t)的草图;(4)求出此人的血压在血压计上的读数.
三角函数模型的实际应用根据图像求解析式 例2、建设生态文明,是关系人民福祉、关乎民族未来的长远大计.某市通宵营业的大型商场,为响应节能减排的号召,在气温超过28 ℃时,才开放中央空调降温,否则关闭中央空调.如图是该市夏季一天的气温(单位:℃)随时间(0≤t≤24,单位:小时)的大致变化曲线,若该曲线近似满足函数关系y=Asin+b(A>0,ω>0,|φ|<π).(1)求函数y=f的表达式;(2)请根据(1)的结论,判断该商场的中央空调应在本天内何时开启?何时关闭?
三角函数模型的实际应用根据表格求解析式 例3、已知某海滨浴场的海浪高度y(米)是时间t(时)的函数,其中0≤t≤24,记y=f(t),下表是某日各时的浪高数据:t03691215182124y1.51.00.51.01.510.50.991.5经长期观测,y=f(t)的图象可近似地看成是函数y=Acos ωt+b的图象.(1)根据以上数据,求其最小正周期,振幅及函数解析式;(2)根据规定,当海浪高度大于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的8:00到20:00之间,有多少时间可供冲浪者进行活动?如何借助表格中的数据探寻与参数A,ω,b的相关量?解三角不等式的关键是什么?
根据实际问题描述求解析式 思考题、如图所示,摩天轮的半径为40 m,O点距地面的高度为50 m,摩天轮作匀速转动,每2 min转一圈,摩天轮上点P的起始位置在最高点.(1)试确定在时刻t min时P点距离地面的高度;(2)在摩天轮转动一圈内,有多长时间P点距离地面超过70 m.
课后作业
一、基础训练题
1.最大值为,最小正周期为,初相为的函数表达式是( )
A.y=sin B.y=sin C.y=sin D.y=sin
2.音叉是呈“Y”形的钢质或铝合金发声器(如图1),各种音叉可因其质量和叉臂长短、粗细不同而在振动时发出不同频率的纯音.敲击某个音叉时,在一定时间内,音叉上点P离开平衡位置的位移y与时间t的函数关系为y=sin ωt.图2是该函数在一个周期内的图象,根据图中数据可确定ω的值为( )
A.200 B.400
C.200π D.400π
3.(多选题)如图所示是一个简谐运动的图象,则下列判断正确的是( )
A.该质点的运动周期为0.8 s
B.该质点的振幅为-5 cm
C.该质点在0.1 s和0.5 s时的振动速度最大 D.该质点在0.3 s和0.7 s时的位移为零
4.商场人流量被定义为每分钟通过入口的人数,五一节那天某商场的人流量满足函数F(t)=50+4sin (t≥0),则在下列时间段内人流量增加的是( )
A.[0,5] B.[5,10] C.[10,15] D.[15,20]
5.下表是某市近30年来月平均气温(℃)的数据统计表:
月份 1 2 3 4 5 6 7 8 9 10 11 12
平均温度 -5.9 -3.3 2.2 9.3 15.1 20.3 22.8 22.2 18.2 11.9 4.3 -2.4
则适合这组数据的函数模型是( )
A.y=acos B.y=acos+k(a>0,k>0)
C.y=-acos+k(a>0,k>0) D.y=acos-3
6.电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)的图象如图所示,则当t=秒时,电流强度是( )
A.-5安 B.5安 C.5安 D.10安
7.一根长l cm的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(cm)与时间t(s)的函数关系式为s=3cos,其中g是重力加速度,当小球摆动的周期是1 s时,线长l=________cm.
8.如图是弹簧振子做简谐振动的图象,横轴表示振动的时间,纵轴表示振动的位移,则这个振子振动的函数解析式是_________________.
9.一种波的波形为函数y=-sinx的图象,若其在区间[0,t]上至少有2个波峰(图象的最高点),则正整数t的最小值是________.
10.已知某地一天从4时到16时的温度变化曲线近似满足函数y=10sin +20,x∈[4,16].
(1)求该地区这一段时间内温度的最大温差;
(2)若有一种细菌在15 ℃到25 ℃之间可以生存,那么在这段时间内,该细菌能生存多长时间?
二、综合训练题
11.稳定房价是我国今年实施宏观调控的重点,国家最近出台的一系列政策已对各地的房地产市场产生了影响,温州市某房地产中介对本市一楼盘在今年的房价作了统计与预测:发现每个季度的平均单价y(每平方米的价格,单位:元)与第x季度之间近似满足:y=500sin(ωx+φ)+9 500(ω>0),已知第一、二季度平均单价如下表所示:
x 1 2 3
y 10 000 9 500 ?
则此楼盘在第三季度的平均单价大约是( )
A.10 000元 B.9 500元
C.9 000元 D.8 500元
12.如图所示,一个大风车的半径为8 m,每12 min旋转一周,最低点离地面2 m.若风车翼片从最低点按逆时针方向开始旋转,则该翼片的端点P离地面的距离h(m)与时间t(min)之间的函数关系是( )
A.h=8cost+10 B.h=-8cost+10C.h=-8sint+10 D.h=-8cost+10
13.为迎接夏季旅游旺季的到来,少林寺单独设置了一个专门安排游客住宿的客栈,寺庙的工作人员发现为游客准备的一些食物有些月份剩余不少,浪费很严重,为了控制经营成本,减少浪费,就想适时调整投入,为此他们统计每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数会发生周期性的变化,并且有以下规律:
①每年相同的月份,入住客栈的游客人数基本相同;
②入住客栈的游客人数在2月份最少,在8月份最多,相差约400人;
③2月份入住客栈的游客约为100人,随后逐月递增直到8月份达到最多.
(1)试用一个正弦型三角函数描述一年中入住客栈的游客人数与月份之间的关系;
(2)请问哪几个月份要准备400份以上的食物?
三、能力提升题
14.如图,设点A是单位圆上的一定点,动点P从点A出发在圆上按逆时针方向旋转一周,点P所旋转过的弧的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )
A B C D
15.国际油价在某一时间内呈现正弦波动规律:P=Asinωπt++60(美元)(t(天),A>0,ω>0),现采集到下列信息:最高油价80美元,当t=150(天)时达到最低油价,则ω的最小值为________.
5.7三角函数的应用
参考答案
1、【答案】D
【解析】由题意可知,周期T==,∴ω=3.∴y=sin,故选D.
2、【答案】D
【解析】由图象可得,ω>0,T=4×=,即=,则ω=400π.
3、【答案】AD
【解析】由图可知T=0.6,∴T=0.8.振幅A=5 cm,当t=0.1 s或0.5 s时,v=0.故选AD.
4、【答案】C
【解析】由2kπ-≤≤2kπ+,k∈Z,知函数F(t)的增区间为[4kπ-π,4kπ+π],k∈Z.
当k=1时,t∈[3π,5π],而[10,15] [3π,5π],故选C.
5、【答案】C
【解析】当x=1时图象处于最低点,且易知a=>0.故选C.
6、【答案】A
【解析】由图象知A=10,=-=,所以ω==100π.所以I=10sin(100πt+φ).
因为为五点作图法中的第二个点,所以100π×+φ=.所以φ=.
所以I=10sin,当t=秒时,I=-5安.
7、【答案】
【解析】由已知得=1,所以=2π,=4π2,l=.]
8、【答案】y=2sin
【解析】由题图可设y=Asin(ωt+φ),则A=2,又T=2(0.5-0.1)=0.8,
所以ω==π,所以y=2sin,将点(0.1,2)代入y=2sin中,得sin=1,
所以φ+=2kπ+,k∈Z,即φ=2kπ+,k∈Z,
令k=0,得φ=,所以y=2sin.
9、【答案】7
【解析】函数y=-sinx的周期T=4,且x=3时y=1取得最大值,因此t≥7.即正整数t的最小值是7.
10、[解] (1)由函数易知,当x=14时函数取最大值,即最高温度为30 ℃;当x=6时函数取最小值,即最低温度为10 ℃.所以,最大温差为30 ℃-10 ℃=20 ℃.
(2)令10sin+20=15,可得sin=-. 而x∈[4,16],所以x=.
令10sin+20=25,可得sin=,而x∈[4,16],
所以x=.故该细菌的存活时间为-=小时.
11、【答案】C
【解析】因为y=500sin(ωx+φ)+9 500(ω>0),所以当x=1时,500sin(ω+φ)+9 500=10 000;
当x=2时,500sin(2ω+φ)+9 500=9 500,所以ω可取,φ可取π,即y=500sin+9 500.
当x=3时,y=9 000.
12、【答案】D
【解析】依题意可设h=Asin(ωt+φ)+B(A>0,ω>0),易知T=12,A=8,B=10,所以ω==,
则h=8sin+10,当t=0时,8sin φ+10=2,得sin φ=-1,可取φ=-,
所以h=8sin+10=-8cost+10.
13、[解析] (1)设该函数为f(x)=Asin(ωx+φ)+B(A>0,ω>0,0<|φ|<π),根据条件①,
可知这个函数的周期是12;由②可知,f(2)最小,f(8)最大,且f(8)-f(2)=400,故该函数的振幅为200;
由③可知,f(x)在[2,8]上单调递增,且f(2)=100,所以f(8)=500.
根据上述分析可得,=12,故ω=,且解得
根据分析可知,当x=2时,f(x)最小,当x=8时,f(x)最大,
故sin=-1,且sin=1.又因为0<|φ|<π,故φ=-.
所以入住客栈的游客人数与月份之间的关系式为f(x)=200sin+300.
(2)由条件可知,200sin+300≥400,
化简,得sin≥ 2kπ+≤x-≤2kπ+,k∈Z,解得12k+6≤x≤12k+10,k∈Z.
因为x∈N*,且1≤x≤12,故x=6,7,8,9,10.
即只有6,7,8,9,10五个月份要准备400份以上的食物.
14、【答案】C
【解析】令AP所对圆心角为θ,由|OA|=1,得l=θ,sin=,∴d=2sin=2sin,
即d=f(l)=2sin(0≤l≤2π),它的图象为C
15、【答案】
【解析】因为Asin+60=80,sin≤1,
所以A=20,当t=150(天)时达到最低油价,即sin=-1,此时150ωπ+=2kπ-,k∈Z,因为ω>0,所以当k=1时,ω取最小值,
所以150ωπ+=π,解得ω=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
