相似三角形的判定
图片预览



文档简介
课件25张PPT。相似三角形的判定
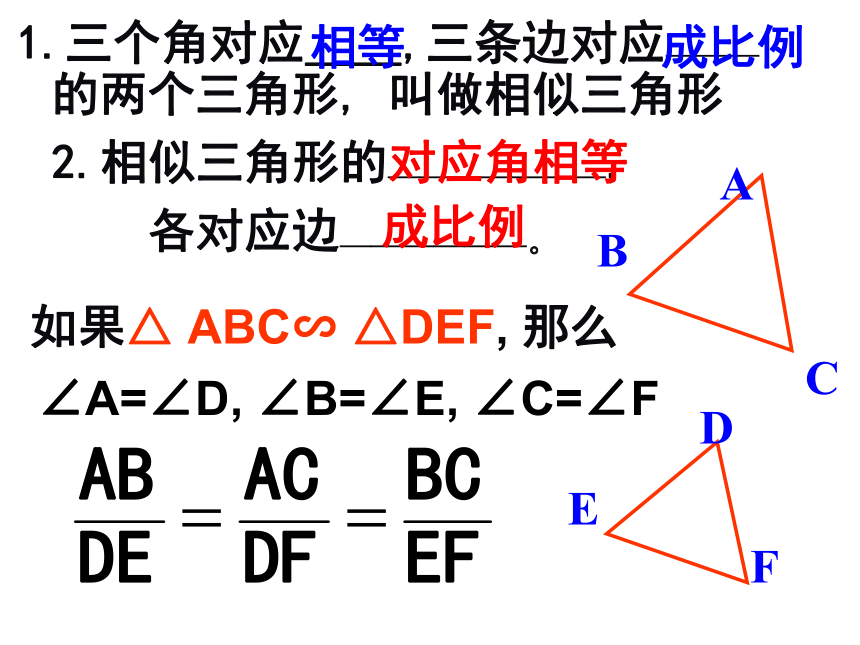
冯家中学 1.三个角对应____,三条边对应———的两个三角形, 叫做相似三角形 相等成比例2.相似三角形的———————,
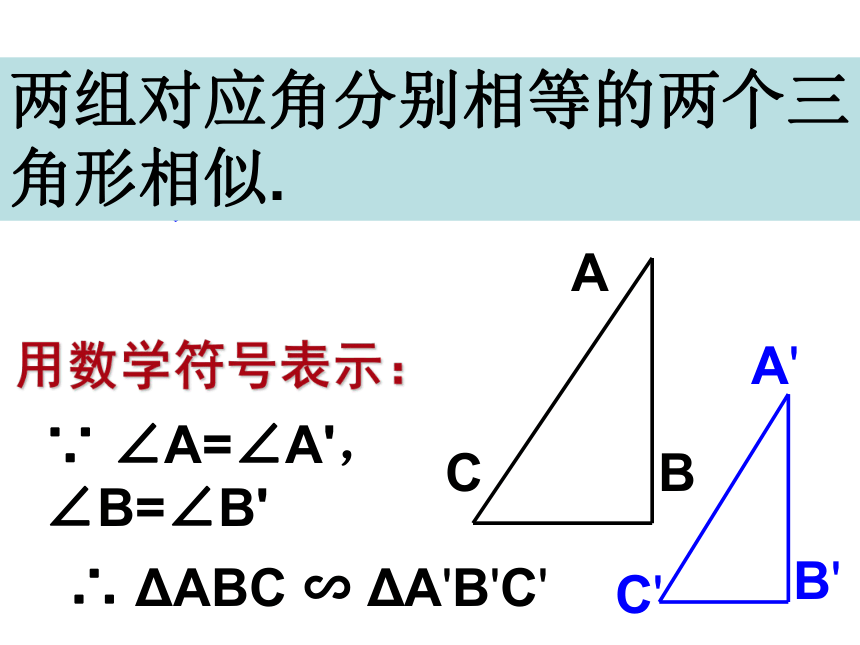
各对应边——————。对应角相等成比例如果△ ABC∽ △DEF, 那么∠A=∠D, ∠B=∠E, ∠C=∠F相似三角形的识别方法1:如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.用数学符号表示:∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'CAA'BB'C'两组对应角分别相等的两个三角形相似.思 考能否再简便一些?
有一对角对应相等的两个三角形相似吗?例1.如图,在两个直角三角形△ABC和△A′B′C′中,∠B=∠B′=90°,∠A=∠A′,证明这两个三角形是否相似. 证明:∵ ∠B=∠B′=90°(已知),
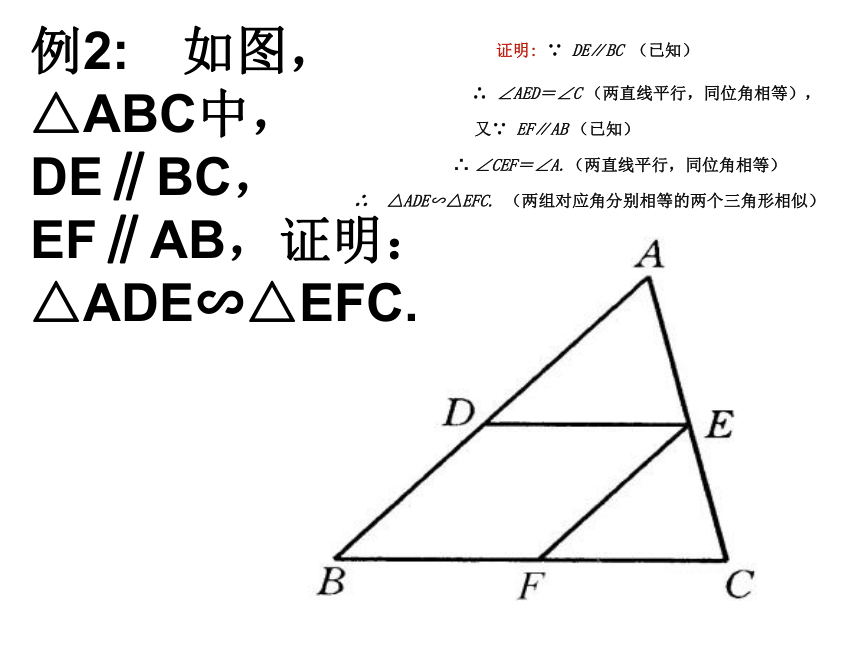
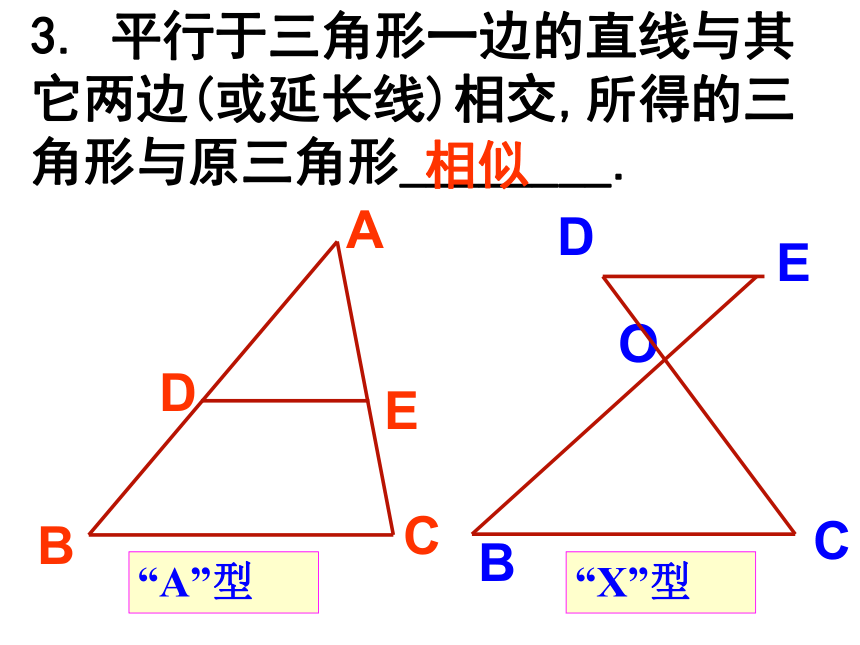
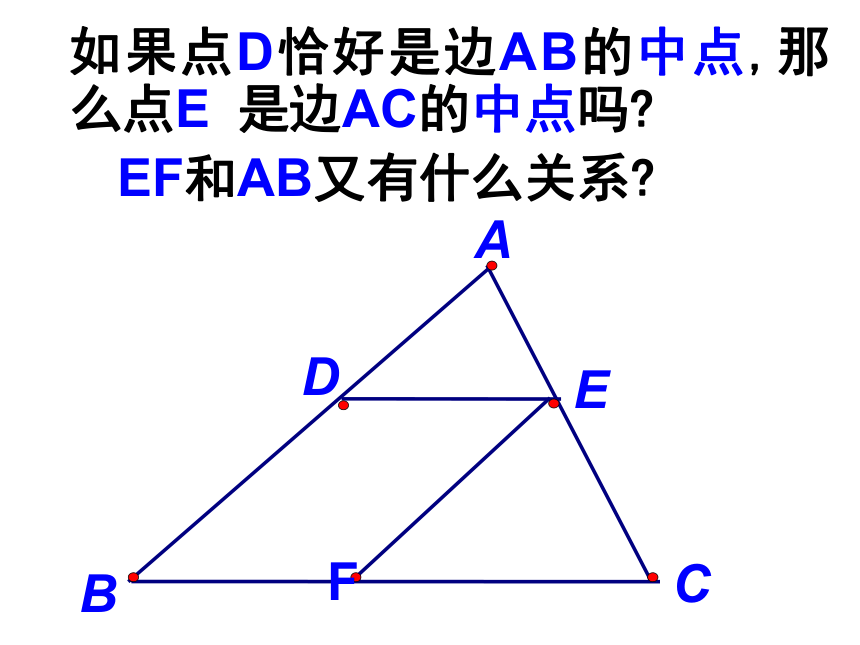
∠A=∠A′(已知), ∴ △ABC∽△A′B′C′(两组对应角分别相等的两个三角形相似) 例2: 如图,△ABC中,DE∥BC,EF∥AB,证明:△ADE∽△EFC.证明: ∵ DE∥BC (已知) ∴ ∠AED=∠C (两直线平行,同位角相等),∴ ∠CEF=∠A.(两直线平行,同位角相等)∴ △ADE∽△EFC. (两组对应角分别相等的两个三角形相似) 又∵ EF∥AB (已知)3. 平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形________.相似“A”型 “X”型 如果点D恰好是边AB的中点,那么点E 是边AC的中点吗?
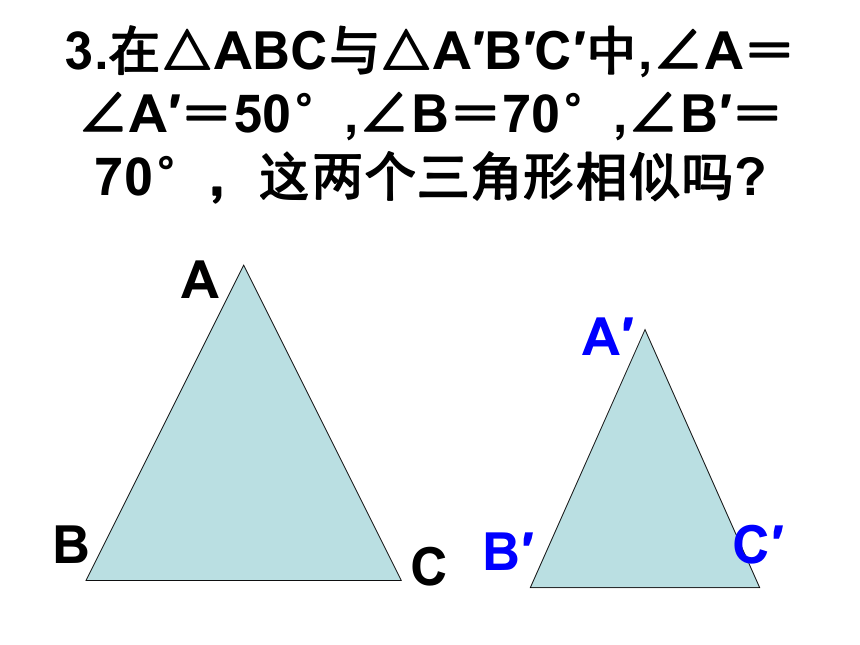
EF和AB又有什么关系? 3.在△ABC与△A′B′C′中,∠A=∠A′=50°,∠B=70°,∠B′=70°,这两个三角形相似吗?ABCA′ B′ C′∠A=∠A′=50° ∠B=70°∠B′=60°这两三角形仍然相似吗? ABCA′ B′ C′ 3、已知直角三角形ABC中,∠ACB=900,CD⊥AB于点D,则:______∽______∽______.△ABC△ACD△CBD直角三角形斜边上的高分成的两个直角三角形与原三角形相似.4、如图、在△ABC中,边AB、AC上的高CE、BD相交于点P,请找出图中所有的相似三角形。△BEP与△CDP△ABD与△ACE4.有一个角等于300的两个等腰三角形相似。 ( )
5.有一对角相等的两个等腰三角形一定相似。 ( )
6.有一组对角相等的三角形一定相似。 ( )×××7.有一对锐角相等的两个直角三角形一定相似。( )
8.有一个角是80 °的两个等腰三角形相似 ( )
9.有一个角是120°的两个等腰三角形相似( ) √×√1.已知,如图若△ABC∽△ACD,需要条件 ;
2.已知,如图若△ABE∽△ACD,需要条件 ;A′B′C′A651°82°它们是相似三角形吗?为什么? 如图,△ABC中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.解: 与△ABC相似的三角形有3个: △ADE △GFC △GOE5. 如图, 在△ABC中,DG∥EH∥FI∥BC,(1)请找出图中所有的相似三角形;(2)如果AD=1,DB=3,那么DG:BC=___ 。△ADG∽△AEH∽△AFI∽△ABC1:41.如图,△ABC中,点D是AB上一点.(1)若∠1=∠B,写出图中的相似三角形.ABC(3) 若:AD=16, DB=9. 求AC的长.(2) 说明 : AC2=AD·ABD2、如图所示,∠ 1= ∠ 3,
∠ C= ∠ E, △ABC 和 △ ADE相似吗?请说明理由。ABCDE 321已知: Rt△ABC 与 Rt△DFE中,∠B与∠F为直角(如图所示)。问能否分别将这两个三角形各分割成两个三角形,使△ABC所分成的两个三角形与△DEF所分成的两个三角形相似?请设计出一种分割方案,并加以分析.┓ABCDFE┓△ABM∽△FEN△MBC∽△NDF
冯家中学 1.三个角对应____,三条边对应———的两个三角形, 叫做相似三角形 相等成比例2.相似三角形的———————,
各对应边——————。对应角相等成比例如果△ ABC∽ △DEF, 那么∠A=∠D, ∠B=∠E, ∠C=∠F相似三角形的识别方法1:如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.用数学符号表示:∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'CAA'BB'C'两组对应角分别相等的两个三角形相似.思 考能否再简便一些?
有一对角对应相等的两个三角形相似吗?例1.如图,在两个直角三角形△ABC和△A′B′C′中,∠B=∠B′=90°,∠A=∠A′,证明这两个三角形是否相似. 证明:∵ ∠B=∠B′=90°(已知),
∠A=∠A′(已知), ∴ △ABC∽△A′B′C′(两组对应角分别相等的两个三角形相似) 例2: 如图,△ABC中,DE∥BC,EF∥AB,证明:△ADE∽△EFC.证明: ∵ DE∥BC (已知) ∴ ∠AED=∠C (两直线平行,同位角相等),∴ ∠CEF=∠A.(两直线平行,同位角相等)∴ △ADE∽△EFC. (两组对应角分别相等的两个三角形相似) 又∵ EF∥AB (已知)3. 平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形________.相似“A”型 “X”型 如果点D恰好是边AB的中点,那么点E 是边AC的中点吗?
EF和AB又有什么关系? 3.在△ABC与△A′B′C′中,∠A=∠A′=50°,∠B=70°,∠B′=70°,这两个三角形相似吗?ABCA′ B′ C′∠A=∠A′=50° ∠B=70°∠B′=60°这两三角形仍然相似吗? ABCA′ B′ C′ 3、已知直角三角形ABC中,∠ACB=900,CD⊥AB于点D,则:______∽______∽______.△ABC△ACD△CBD直角三角形斜边上的高分成的两个直角三角形与原三角形相似.4、如图、在△ABC中,边AB、AC上的高CE、BD相交于点P,请找出图中所有的相似三角形。△BEP与△CDP△ABD与△ACE4.有一个角等于300的两个等腰三角形相似。 ( )
5.有一对角相等的两个等腰三角形一定相似。 ( )
6.有一组对角相等的三角形一定相似。 ( )×××7.有一对锐角相等的两个直角三角形一定相似。( )
8.有一个角是80 °的两个等腰三角形相似 ( )
9.有一个角是120°的两个等腰三角形相似( ) √×√1.已知,如图若△ABC∽△ACD,需要条件 ;
2.已知,如图若△ABE∽△ACD,需要条件 ;A′B′C′A651°82°它们是相似三角形吗?为什么? 如图,△ABC中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.解: 与△ABC相似的三角形有3个: △ADE △GFC △GOE5. 如图, 在△ABC中,DG∥EH∥FI∥BC,(1)请找出图中所有的相似三角形;(2)如果AD=1,DB=3,那么DG:BC=___ 。△ADG∽△AEH∽△AFI∽△ABC1:41.如图,△ABC中,点D是AB上一点.(1)若∠1=∠B,写出图中的相似三角形.ABC(3) 若:AD=16, DB=9. 求AC的长.(2) 说明 : AC2=AD·ABD2、如图所示,∠ 1= ∠ 3,
∠ C= ∠ E, △ABC 和 △ ADE相似吗?请说明理由。ABCDE 321已知: Rt△ABC 与 Rt△DFE中,∠B与∠F为直角(如图所示)。问能否分别将这两个三角形各分割成两个三角形,使△ABC所分成的两个三角形与△DEF所分成的两个三角形相似?请设计出一种分割方案,并加以分析.┓ABCDFE┓△ABM∽△FEN△MBC∽△NDF
