期末计算专题 多边形的面积真题汇编(含答案)数学五年级上册人教版
文档属性
| 名称 | 期末计算专题 多边形的面积真题汇编(含答案)数学五年级上册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 16:10:03 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
期末计算专题:多边形的面积(真题汇编)数学五年级上册人教版
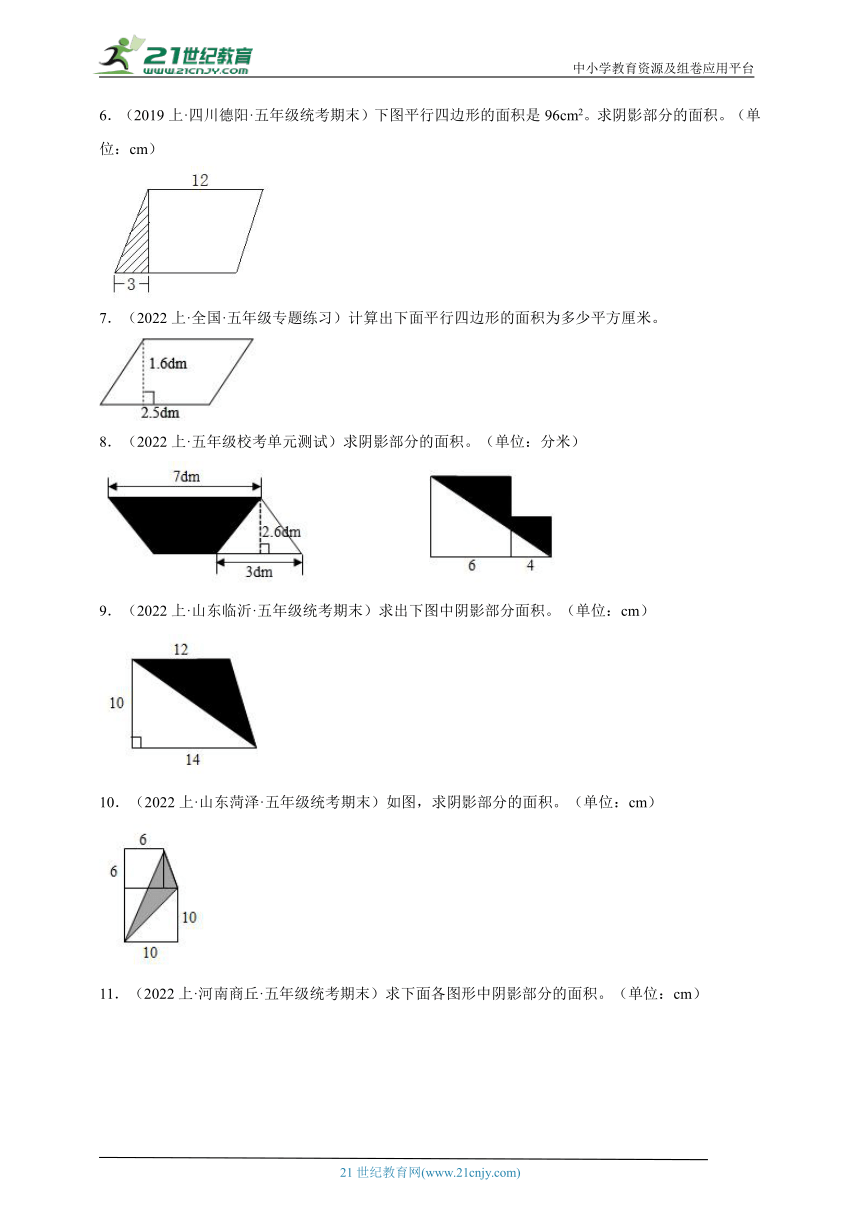
1.(2022上·海南省直辖县级单位·五年级校考期末)求下列图形的面积。
2.(2022上·甘肃陇南·五年级统考期末)求下图中阴影部分的面积。(单位:cm)
3.(2022上·山西忻州·五年级校考期中)计算下面图形的面积。(单位:cm)
4.(2022上·全国·五年级专题练习)求下面图形的面积。
5.(2019上·浙江丽水·五年级统考期末)下图中阴影部分是一块草坪的平面图,求这块草坪的面积。
6.(2019上·四川德阳·五年级统考期末)下图平行四边形的面积是96cm2。求阴影部分的面积。(单位:cm)
7.(2022上·全国·五年级专题练习)计算出下面平行四边形的面积为多少平方厘米。
8.(2022上·五年级校考单元测试)求阴影部分的面积。(单位:分米)
9.(2022上·山东临沂·五年级统考期末)求出下图中阴影部分面积。(单位:cm)
10.(2022上·山东菏泽·五年级统考期末)如图,求阴影部分的面积。(单位:cm)
11.(2022上·河南商丘·五年级统考期末)求下面各图形中阴影部分的面积。(单位:cm)
(1) (2)
12.(2022上·山东菏泽·五年级统考期末)计算下图的面积。(单位:厘米)
13.(2022上·山东菏泽·五年级统考期末)求图中阴影部分的面积。(单位:厘米)
14.(2022上·湖南怀化·五年级统考期末)已知如图,两个正方形的边长是8cm和3cm。求阴影部分的面积。
15.(2022上·浙江温州·五年级统考期末)求图中阴影部分的面积。
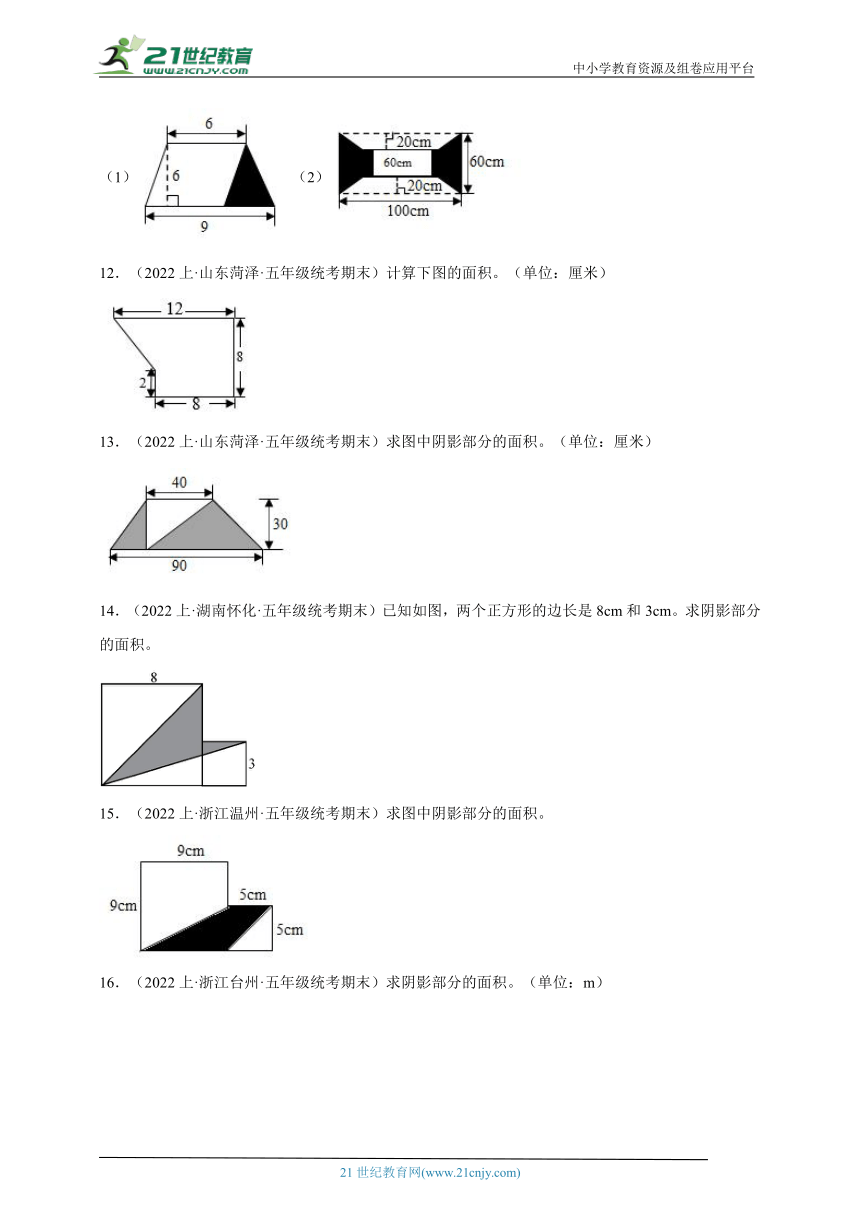
16.(2022上·浙江台州·五年级统考期末)求阴影部分的面积。(单位:m)
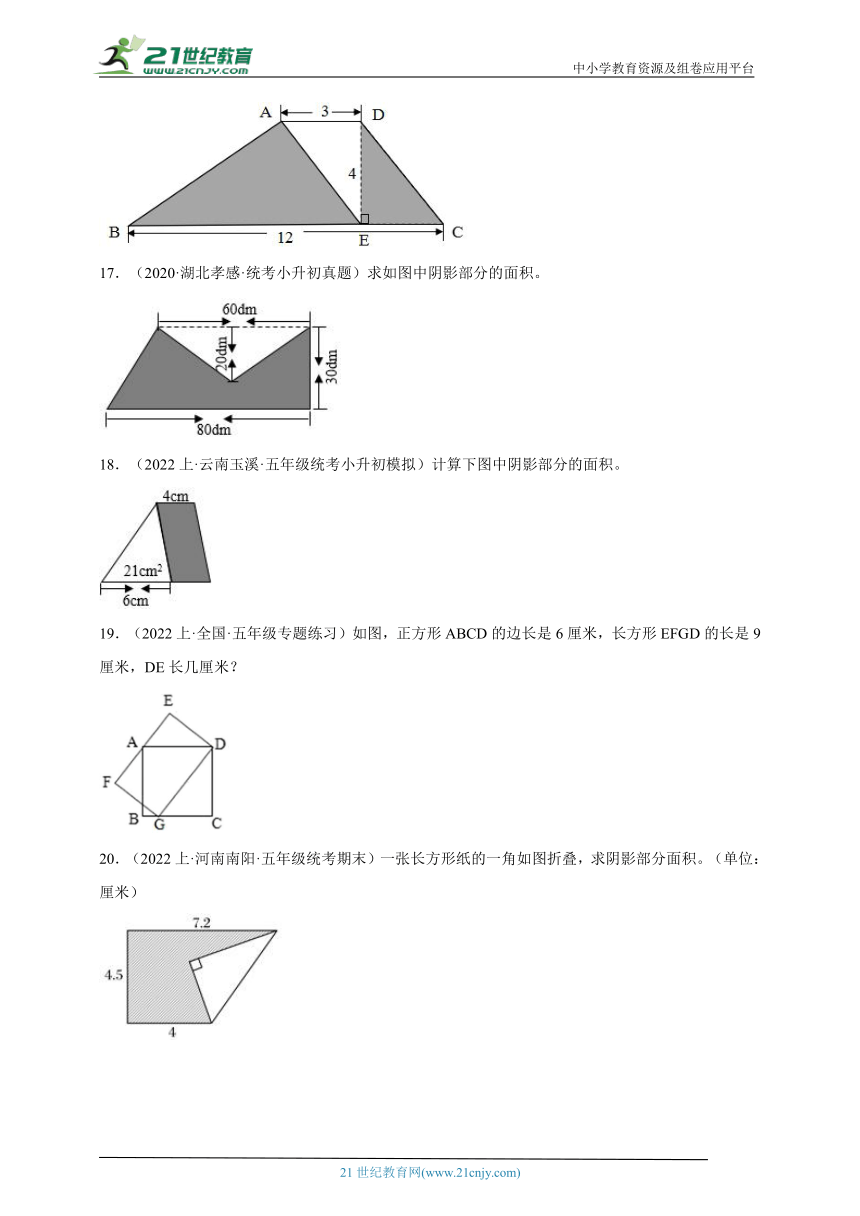
17.(2020·湖北孝感·统考小升初真题)求如图中阴影部分的面积。
18.(2022上·云南玉溪·五年级统考小升初模拟)计算下图中阴影部分的面积。
19.(2022上·全国·五年级专题练习)如图,正方形ABCD的边长是6厘米,长方形EFGD的长是9厘米,DE长几厘米?
20.(2022上·河南南阳·五年级统考期末)一张长方形纸的一角如图折叠,求阴影部分面积。(单位:厘米)
参考答案:
1.28平方厘米;30平方厘米
【分析】(1)平行四边形的面积=底×高,由图可知,平行四边形的底为7cm,对应的高为4cm;
(2)图形的面积=三角形的面积+正方形的面积,据此解答。
【详解】(1)7×4=28(平方厘米)
(2)5×2÷2+5×5
=5+25
=30(平方厘米)
2.84平方厘米
【分析】阴影部分是以14厘米为底,12厘米为高的三角形,利用三角形的面积计算公式即可求得。
【详解】14×12÷2
=168÷2
=84(平方厘米)
所以,阴影部分的面积是84平方厘米。
3.7.5平方厘米;129平方厘米
【分析】根据题干可知:
(1)组合图形的面积=两个三角形面积之和;
(2)图形面积=长方形面积-梯形面积,代入数即可。
【详解】(1)3×3÷2+3×2÷2
=4.5+3
=7.5(平方厘米)
(2)16×9-(4+6)×3÷2
=144-15
=129(平方厘米)
4.340平方厘米;260平方米
【分析】“平行四边形的面积=底×高”,“三角形的面积=底×高÷2”据此解答即可。
【详解】17×20=340(平方厘米);
20×8+20×10÷2
=160+100
=260(平方米)
5.375平方米
【分析】观察图形可知,阴影部分的面积=长方形的面积-梯形的面积,据此代入数值进行计算即可。
【详解】20×30-(20+30)×9÷2
=600-450÷2
=600-225
=375(平方米)
6.12平方厘米
【分析】用96÷12求出平行四边形的高,也就是三角形的高,再根据“三角形的面积=底×高÷2”进行解答即可。
【详解】3×(96÷12)÷2
=3×8÷2
=12(平方厘米);
阴影部分的面积为12平方厘米。
7.400平方厘米
【分析】根据平行四边形的面积=底×高,据此代入数值进行计算即可。
【详解】2.5×1.6=4(平方分米)=400(平方厘米)
8.14.3平方分米;22平方分米
【分析】第一个图阴影部分的面积=平行四边形的面积-三角形的面积;
第二个图阴影部分的面积=两个正方形的面积和-三角形的面积。
【详解】7×2.6-3×2.6÷2
=18.2-3.9
=14.3(平方分米);
6×6+4×4-(6+4)×6÷2
=52-30
=22(平方分米)
9.60cm2
【分析】阴影部分的面积=梯形面积-空白三角形的面积,代入数据计算即可。
【详解】(12+14)×10÷2-14×10÷2
=26×10÷2-140÷2
=60(cm2)
10.50cm2
【分析】阴影部分的面积=两个正方形的面积和-两个空白三角形面积和+两个正方形外的阴影三角形的面积;据此解答。
【详解】两个正方形面积:10×10+6×6
=100+36
=136(平方厘米)
两个空白三角形面积:10×10÷2+6×(6+10)÷2
=50+48
=98(平方厘米)
两个正方形外的阴影三角形的面积:(10-6)×6÷2
=24÷2
=12
阴影部分面积:136-98+12=50(平方厘米)
11.9平方厘米;2800平方厘米
【分析】(1)阴影部分是一个三角形直接利用三角形的面积公式即可求得;
(2)阴影部分面积=长方形面积-梯形的面积×2。
【详解】(1)(9-6)×6÷2
=3×6÷2
=18÷2
=9(平方厘米)
(2)100×60-(60+100)×20÷2×2
=100×60-160×20÷2×2
=6000-3200
=2800(平方厘米)
12.76平方厘米
【分析】用分割法把图形分为一个正方形和一个三角形,总面积=正方形的面积+三角形的面积。
【详解】
8×8+(12-8)×(8-2)÷2
=8×8+4×6÷2
=64+12
=76(平方厘米)
13.1350平方厘米
【分析】阴影部分的面积=梯形的面积-空白部分三角形的面积。
【详解】(90+40)×30÷2-40×30÷2
=130×30÷2-40×30÷2
=3900÷2-1200÷2
=1950-600
=1350(平方厘米)
所以,阴影部分面积是1350平方厘米。
14.24.5平方厘米
【分析】给阴影部分添加一条线,发现阴影部分的面积是2个三角形面积的和。三角形的面积=底×高÷2,根据图意找出每个三角形的底和高,把数据代入公式计算即可。
【详解】如下图,给阴影部分添加一条线,分成两个三角形,
(8-3)×8÷2+3×3÷2
=5×8÷2+9÷2
=20+4.5
=24.5(平方厘米)
15.35平方厘米
【分析】观察图形发现,阴影部分是一个梯形,它的上底是5厘米、高是5厘米、下底与正方形的边长相等,是9厘米;据此根据梯形面积=(上底+下底)×高÷2,即可计算出阴影部分的面积。
【详解】(5+9)×5÷2
=14×5÷2
=70÷2
=35(平方厘米)
所以,图中阴影部分的面积是35平方厘米。
16.24平方米
【分析】阴影部分的面积=梯形面积-三角形面积,梯形面积=(上底+下底)×高÷2,三角形面积=底×高÷2。
【详解】(3+12)×4÷2-3×4÷2
=15×2-6
=30-6
=24(平方米)
【点睛】关键是观察组合图形的特点,掌握梯形和三角形面积公式。
17.1500dm2
【分析】涂色部分的面积=梯形的面积-三角形的面积,梯形的面积公式是S=(a+b)h÷2,三角形的面积公式是S=ah÷2。
【详解】(60+80)×30÷2-60×20÷2
=2100-600
=1500(dm2)
18.28()
【分析】阴影部分是一个平行四边形,它的高和三角形的高相等,据公式:三角形的面积=底×高÷2,推出三角形的高=三角形的面积×2÷底,再利用公式:平行四边形的面积=底×高,据此求出阴影部分的面积即可。
【详解】21×2÷6×4
=42÷6×4
=7×4
=28()
【点睛】知道阴影部分的高和三角形的高相等,根据三角形面积公式计算出高,这是解决此题的关键。
19.4厘米
【分析】
如图所示,连接AG,△AGD的面积等于正方形的面积的一半。由DG同底,高相等得到△AGD的面积也等于长方形EFGD的面积的一半,正方形的边长已知,于是可以求出△AGD的面积,进而可以求出长方形的面积,再根据长方形的面积公式即可求出长方形的宽,即DE的长。
【详解】6×6÷2=18(平方厘米)
18×2÷9=4(厘米)
则DE的长是4厘米。
20.18平方厘米
【分析】根据图形折叠的方法可知,原来长方形的长是7.2厘米,宽是4.5厘米,则白色三角形的两条直角边分别是4.5厘米和7.2-4=3.2厘米,则图中阴影部分的面积=梯形的面积-白色三角形的面积,由此利用梯形和三角形的面积公式即可解答。
【详解】(4+7.2)×4.5÷2-(7.2-4)×4.5÷2
=11.2×4.5÷2-3.2×4.5÷2
=(11.2-3.2)×4.5÷2
=8×4.5÷2
=18(平方厘米)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末计算专题:多边形的面积(真题汇编)数学五年级上册人教版
1.(2022上·海南省直辖县级单位·五年级校考期末)求下列图形的面积。
2.(2022上·甘肃陇南·五年级统考期末)求下图中阴影部分的面积。(单位:cm)
3.(2022上·山西忻州·五年级校考期中)计算下面图形的面积。(单位:cm)
4.(2022上·全国·五年级专题练习)求下面图形的面积。
5.(2019上·浙江丽水·五年级统考期末)下图中阴影部分是一块草坪的平面图,求这块草坪的面积。
6.(2019上·四川德阳·五年级统考期末)下图平行四边形的面积是96cm2。求阴影部分的面积。(单位:cm)
7.(2022上·全国·五年级专题练习)计算出下面平行四边形的面积为多少平方厘米。
8.(2022上·五年级校考单元测试)求阴影部分的面积。(单位:分米)
9.(2022上·山东临沂·五年级统考期末)求出下图中阴影部分面积。(单位:cm)
10.(2022上·山东菏泽·五年级统考期末)如图,求阴影部分的面积。(单位:cm)
11.(2022上·河南商丘·五年级统考期末)求下面各图形中阴影部分的面积。(单位:cm)
(1) (2)
12.(2022上·山东菏泽·五年级统考期末)计算下图的面积。(单位:厘米)
13.(2022上·山东菏泽·五年级统考期末)求图中阴影部分的面积。(单位:厘米)
14.(2022上·湖南怀化·五年级统考期末)已知如图,两个正方形的边长是8cm和3cm。求阴影部分的面积。
15.(2022上·浙江温州·五年级统考期末)求图中阴影部分的面积。
16.(2022上·浙江台州·五年级统考期末)求阴影部分的面积。(单位:m)
17.(2020·湖北孝感·统考小升初真题)求如图中阴影部分的面积。
18.(2022上·云南玉溪·五年级统考小升初模拟)计算下图中阴影部分的面积。
19.(2022上·全国·五年级专题练习)如图,正方形ABCD的边长是6厘米,长方形EFGD的长是9厘米,DE长几厘米?
20.(2022上·河南南阳·五年级统考期末)一张长方形纸的一角如图折叠,求阴影部分面积。(单位:厘米)
参考答案:
1.28平方厘米;30平方厘米
【分析】(1)平行四边形的面积=底×高,由图可知,平行四边形的底为7cm,对应的高为4cm;
(2)图形的面积=三角形的面积+正方形的面积,据此解答。
【详解】(1)7×4=28(平方厘米)
(2)5×2÷2+5×5
=5+25
=30(平方厘米)
2.84平方厘米
【分析】阴影部分是以14厘米为底,12厘米为高的三角形,利用三角形的面积计算公式即可求得。
【详解】14×12÷2
=168÷2
=84(平方厘米)
所以,阴影部分的面积是84平方厘米。
3.7.5平方厘米;129平方厘米
【分析】根据题干可知:
(1)组合图形的面积=两个三角形面积之和;
(2)图形面积=长方形面积-梯形面积,代入数即可。
【详解】(1)3×3÷2+3×2÷2
=4.5+3
=7.5(平方厘米)
(2)16×9-(4+6)×3÷2
=144-15
=129(平方厘米)
4.340平方厘米;260平方米
【分析】“平行四边形的面积=底×高”,“三角形的面积=底×高÷2”据此解答即可。
【详解】17×20=340(平方厘米);
20×8+20×10÷2
=160+100
=260(平方米)
5.375平方米
【分析】观察图形可知,阴影部分的面积=长方形的面积-梯形的面积,据此代入数值进行计算即可。
【详解】20×30-(20+30)×9÷2
=600-450÷2
=600-225
=375(平方米)
6.12平方厘米
【分析】用96÷12求出平行四边形的高,也就是三角形的高,再根据“三角形的面积=底×高÷2”进行解答即可。
【详解】3×(96÷12)÷2
=3×8÷2
=12(平方厘米);
阴影部分的面积为12平方厘米。
7.400平方厘米
【分析】根据平行四边形的面积=底×高,据此代入数值进行计算即可。
【详解】2.5×1.6=4(平方分米)=400(平方厘米)
8.14.3平方分米;22平方分米
【分析】第一个图阴影部分的面积=平行四边形的面积-三角形的面积;
第二个图阴影部分的面积=两个正方形的面积和-三角形的面积。
【详解】7×2.6-3×2.6÷2
=18.2-3.9
=14.3(平方分米);
6×6+4×4-(6+4)×6÷2
=52-30
=22(平方分米)
9.60cm2
【分析】阴影部分的面积=梯形面积-空白三角形的面积,代入数据计算即可。
【详解】(12+14)×10÷2-14×10÷2
=26×10÷2-140÷2
=60(cm2)
10.50cm2
【分析】阴影部分的面积=两个正方形的面积和-两个空白三角形面积和+两个正方形外的阴影三角形的面积;据此解答。
【详解】两个正方形面积:10×10+6×6
=100+36
=136(平方厘米)
两个空白三角形面积:10×10÷2+6×(6+10)÷2
=50+48
=98(平方厘米)
两个正方形外的阴影三角形的面积:(10-6)×6÷2
=24÷2
=12
阴影部分面积:136-98+12=50(平方厘米)
11.9平方厘米;2800平方厘米
【分析】(1)阴影部分是一个三角形直接利用三角形的面积公式即可求得;
(2)阴影部分面积=长方形面积-梯形的面积×2。
【详解】(1)(9-6)×6÷2
=3×6÷2
=18÷2
=9(平方厘米)
(2)100×60-(60+100)×20÷2×2
=100×60-160×20÷2×2
=6000-3200
=2800(平方厘米)
12.76平方厘米
【分析】用分割法把图形分为一个正方形和一个三角形,总面积=正方形的面积+三角形的面积。
【详解】
8×8+(12-8)×(8-2)÷2
=8×8+4×6÷2
=64+12
=76(平方厘米)
13.1350平方厘米
【分析】阴影部分的面积=梯形的面积-空白部分三角形的面积。
【详解】(90+40)×30÷2-40×30÷2
=130×30÷2-40×30÷2
=3900÷2-1200÷2
=1950-600
=1350(平方厘米)
所以,阴影部分面积是1350平方厘米。
14.24.5平方厘米
【分析】给阴影部分添加一条线,发现阴影部分的面积是2个三角形面积的和。三角形的面积=底×高÷2,根据图意找出每个三角形的底和高,把数据代入公式计算即可。
【详解】如下图,给阴影部分添加一条线,分成两个三角形,
(8-3)×8÷2+3×3÷2
=5×8÷2+9÷2
=20+4.5
=24.5(平方厘米)
15.35平方厘米
【分析】观察图形发现,阴影部分是一个梯形,它的上底是5厘米、高是5厘米、下底与正方形的边长相等,是9厘米;据此根据梯形面积=(上底+下底)×高÷2,即可计算出阴影部分的面积。
【详解】(5+9)×5÷2
=14×5÷2
=70÷2
=35(平方厘米)
所以,图中阴影部分的面积是35平方厘米。
16.24平方米
【分析】阴影部分的面积=梯形面积-三角形面积,梯形面积=(上底+下底)×高÷2,三角形面积=底×高÷2。
【详解】(3+12)×4÷2-3×4÷2
=15×2-6
=30-6
=24(平方米)
【点睛】关键是观察组合图形的特点,掌握梯形和三角形面积公式。
17.1500dm2
【分析】涂色部分的面积=梯形的面积-三角形的面积,梯形的面积公式是S=(a+b)h÷2,三角形的面积公式是S=ah÷2。
【详解】(60+80)×30÷2-60×20÷2
=2100-600
=1500(dm2)
18.28()
【分析】阴影部分是一个平行四边形,它的高和三角形的高相等,据公式:三角形的面积=底×高÷2,推出三角形的高=三角形的面积×2÷底,再利用公式:平行四边形的面积=底×高,据此求出阴影部分的面积即可。
【详解】21×2÷6×4
=42÷6×4
=7×4
=28()
【点睛】知道阴影部分的高和三角形的高相等,根据三角形面积公式计算出高,这是解决此题的关键。
19.4厘米
【分析】
如图所示,连接AG,△AGD的面积等于正方形的面积的一半。由DG同底,高相等得到△AGD的面积也等于长方形EFGD的面积的一半,正方形的边长已知,于是可以求出△AGD的面积,进而可以求出长方形的面积,再根据长方形的面积公式即可求出长方形的宽,即DE的长。
【详解】6×6÷2=18(平方厘米)
18×2÷9=4(厘米)
则DE的长是4厘米。
20.18平方厘米
【分析】根据图形折叠的方法可知,原来长方形的长是7.2厘米,宽是4.5厘米,则白色三角形的两条直角边分别是4.5厘米和7.2-4=3.2厘米,则图中阴影部分的面积=梯形的面积-白色三角形的面积,由此利用梯形和三角形的面积公式即可解答。
【详解】(4+7.2)×4.5÷2-(7.2-4)×4.5÷2
=11.2×4.5÷2-3.2×4.5÷2
=(11.2-3.2)×4.5÷2
=8×4.5÷2
=18(平方厘米)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
