期末应用题特训:圆(易错篇)数学六年级上册人教版(含解析)
文档属性
| 名称 | 期末应用题特训:圆(易错篇)数学六年级上册人教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-10 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
期末应用题特训:圆(易错篇)数学六年级上册人教版
1.在一个直径是25m的圆形场地周围栽树.每隔1.57m 栽一棵,一共可以栽多少棵
2.丽丽想用一根长18cm的彩带装饰一个半径为3cm的圆形化妆镜,请你估一估,彩带够吗?为什么?
3.一辆自行车的外轮直径是60cm,如果平均每分钟转100圈,通过一座长3768m的大桥,需要多少分钟?
4.用一根长8米的绳子围着一棵树绕4圈,还余1.72米。这棵树的直径约是多少米?
5.请先画出一个长是3厘米,宽是2厘米的长方形,再在这个长方形中画一个最大的圆,然后求出这个圆形的面积.
6.一个圆的半径是6厘米,在这个圆内画一个最大的正方形。这个正方形的面积是多少平方厘米?
7.如图是一个环形,已知圆环宽度是1米.
(1)如果圆环的小圆直径是10米,那么大圆周长比小圆周长长多少米?
(2)当小圆直径是d米时,大圆周长比小圆周长长多少米?
建议:小圆直径是d米,大圆的直径是d+…,建议列出综合算式解答.
(3)完成以上2题后,你有什么发现?如果圆环的宽度还是1米,小圆直径是2015米,大圆周长比小圆周长长 米.
提示:不需写过程,直接填答案
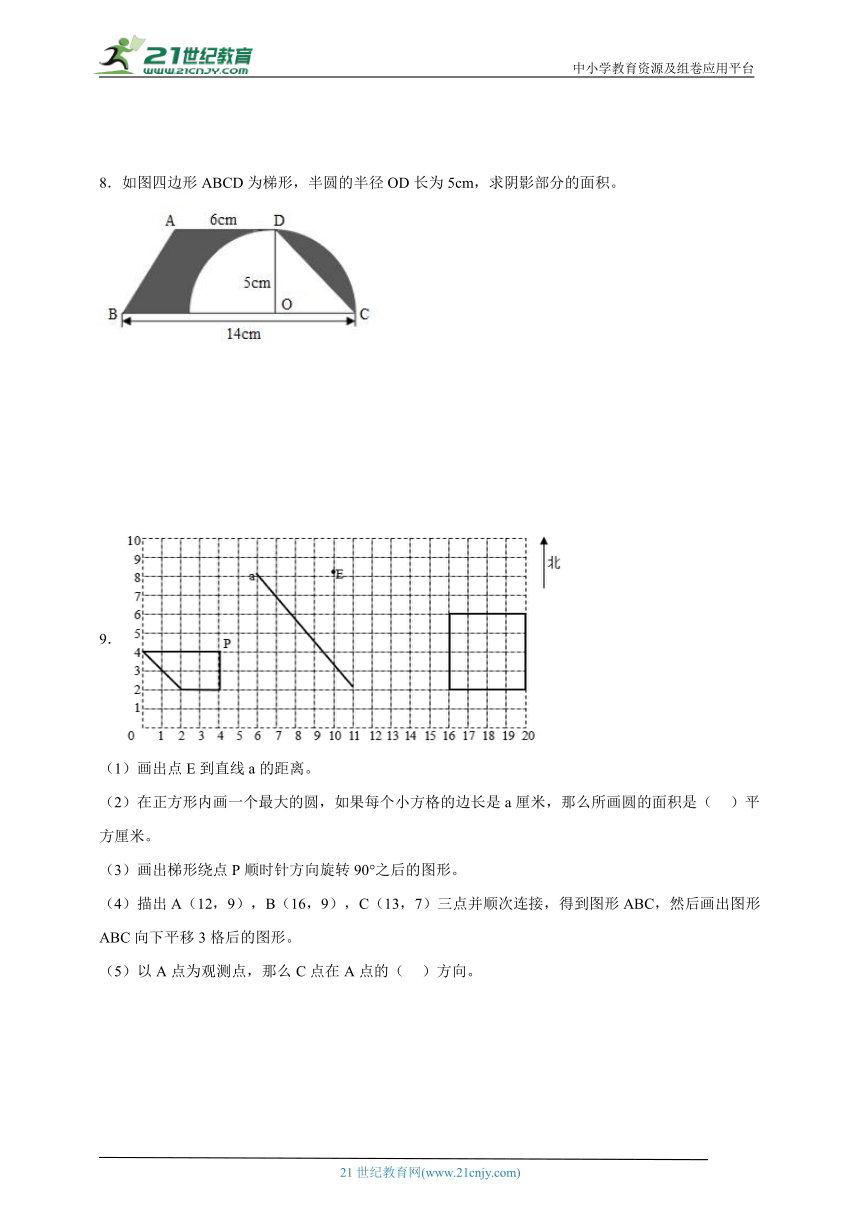
8.如图四边形ABCD为梯形,半圆的半径OD长为5cm,求阴影部分的面积。
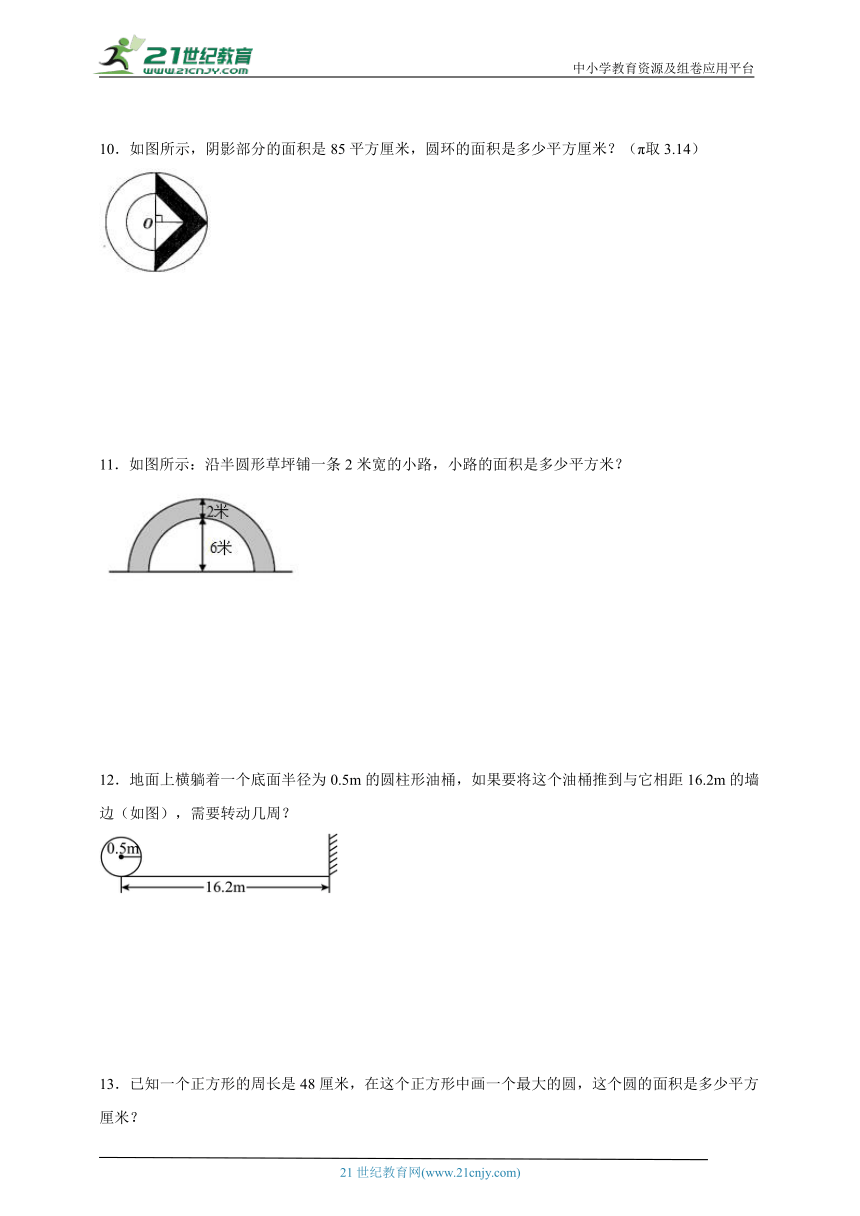
9.
(1)画出点E到直线a的距离。
(2)在正方形内画一个最大的圆,如果每个小方格的边长是a厘米,那么所画圆的面积是( )平方厘米。
(3)画出梯形绕点P顺时针方向旋转90°之后的图形。
(4)描出A(12,9),B(16,9),C(13,7)三点并顺次连接,得到图形ABC,然后画出图形ABC向下平移3格后的图形。
(5)以A点为观测点,那么C点在A点的( )方向。
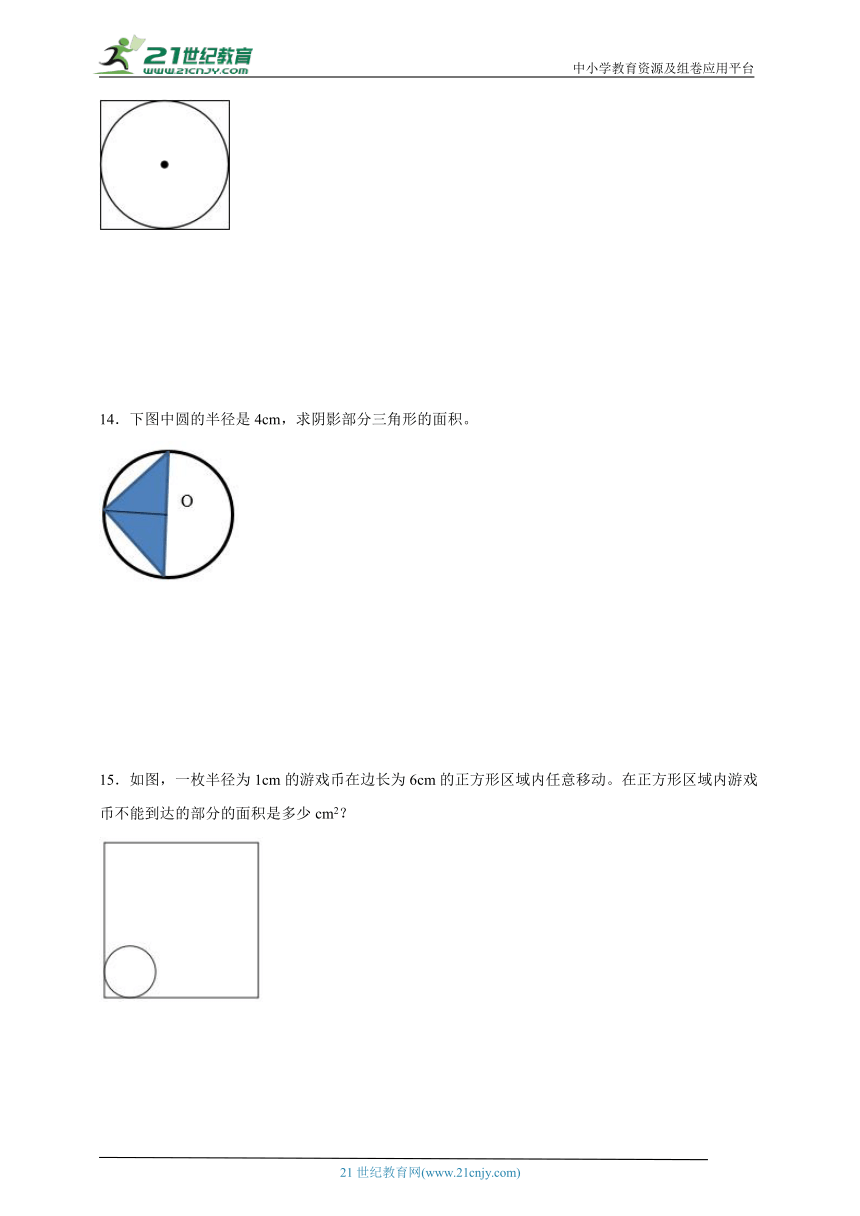
10.如图所示,阴影部分的面积是85平方厘米,圆环的面积是多少平方厘米?(π取3.14)
11.如图所示:沿半圆形草坪铺一条2米宽的小路,小路的面积是多少平方米?
12.地面上横躺着一个底面半径为0.5m的圆柱形油桶,如果要将这个油桶推到与它相距16.2m的墙边(如图),需要转动几周?
13.已知一个正方形的周长是48厘米,在这个正方形中画一个最大的圆,这个圆的面积是多少平方厘米?
14.下图中圆的半径是4cm,求阴影部分三角形的面积。
15.如图,一枚半径为1cm的游戏币在边长为6cm的正方形区域内任意移动。在正方形区域内游戏币不能到达的部分的面积是多少cm2?
16.王老师读小学时,华蓥市的标志性建筑之一——钟鼓楼(如图)十分高大,楼上的钟面上的时针大约长3米,那么它一天走过的面积大约有多少平方米?
17.维维在方格纸中绘制图案,他只完成了整幅作品的。(如下图)
(1)维维完成的图案面积是多少平方厘米?
(2)将整幅作品补充完整,并计算整幅作品的面积。
18.刘大爷用篱笆靠墙围一个半圆形(直径靠墙)的养鸡场,篱笆的长度为15.7米。这个养鸡场的面积是多少平方米?
19.某开发区大标语牌上要画出如下图所示的三种标点符号:句号、逗号、问号。已知大圆半径相同,都为R;小圆半径也相同,都为r;而且。如果都是均匀用料,画哪个标点符号的油漆用得最多?
20.实验小学六年级在一个长方形的场地开展集体舞活动演练,并在场地中进行队列变换。
(1)如果长方形长约66米,长方形场地长与宽的比是4∶3。那么这个场地的宽大约是多少米?
(2)如果从中选出100名同学,在场地中两臂展开围成一个尽可能大的请判断这个场地能否容纳下这个圆,并说明理由。(同学们两臂展开的平均距离是1.5米)
21.计算长方形ABDC绕点D顺时针旋转45°时,CD边扫过的面积。
22.计算并回答下面的问题。
如图所示,大圆中有两个小圆,且两个小圆的直径和正好等于大圆的直径。请问:大圆的周长与两个小圆周长的和相比,谁大些?大圆中阴影部分的面积与两个小圆面积的和相比,谁大些?
23.小军家的煤气灶台面板被油渍弄污了,妈妈要清洁面板。已知这个灶台面板长75厘米、宽42厘米,锅撑圈直径是22厘米,清污(锅撑圈部分除外)的面积是多少平方厘米?
24.在一块边长6分米的正方形铁皮上剪去4个大小相等的圆(如图),剩下的铁皮面积是多少平方分米?
参考答案:
1.50棵
【详解】3.14×25÷1.57=50(棵)
2.不够;估小了还不够,精确计算更不够
【分析】根据圆的周长=2πr,求出化妆镜周长,与彩带长度比较即可。
【详解】2×3.14×3≈18(厘米)
18=18
答:彩带不够,因为将π看成3估出来还不够,看成3.14肯定不够。
【点睛】关键是掌握圆的周长公式。
3.20分钟
【分析】根据圆的周长公式C=πd,先求出自行车外轮转一圈走的路程,再乘100圈,即是自行车外轮平均每分钟走的路程;求通过一座大桥需要的时间,根据时间=路程÷速度,用大桥的长度除以自行车每分钟走的路程即可;注意单位的换算:1m=100cm。
【详解】3.14×60×100
=188.4×100
=18840(cm)
3768m=376800cm
376800÷18840=20(分钟)
答:需要20分钟。
【点睛】掌握圆的周长公式,明确速度、时间、路程三者之间的关系解题的关键。
4.0.5米
【分析】在绳子的总长中减去剩余的1.72米,既是这个树干的4个周长,就可求出这棵树的直径。
【详解】
=6.28÷4÷3.14
=1.57÷3.14
=0.5(米)
答:这棵树的直径约是0.5米。
5.如图,面积是3.14平方厘米
【详解】试题分析:根据所给条件,先画一个长3厘米,宽2厘米的长方形,再以长方形的对角线的交点为圆心,以2÷2=1厘米为半径,即可画出符合要求的圆,然后再求出这个圆的面积.
解:先画一个长3厘米,宽2厘米的长方形,再长方形内画一个直径是2厘米的圆;
这个圆的面积是:3.14×(2÷2)2=3.14×1=3.14(平方厘米);
如图:
.
点评:本题是考查指定长、宽画长方形,指定半径画圆及圆面积的计算.画圆时,圆心决定圆的位置,半径(直径)决定圆的大小.
6.72平方厘米
【分析】根据题意,在圆内画一个最大的正方形,用正方形的一条对角线把这个正方形分成两个完全一样的三角形,三角形的底等于圆的直径,三角形的高等于圆的半径,根据三角形的面积=底×高÷2,即可求出一个三角形的面积,再乘2,就是这个正方形的面积。
【详解】圆的直径:6×2=12(厘米)
三角形的面积:
12×6÷2
=72÷2
=36(平方厘米)
正方形的面积:
36×2=72(平方厘米)
答:这个正方形的面积是72平方厘米。
【点睛】掌握圆内最大正方形的面积求法,把正方形的面积转移到两个三角形的面积上,找出三角形的底、高与圆的半径的关系,然后运用三角形的面积公式求解。
7.(1)6.28米 (2)2π米 (3)发现大圆周长比小圆周长长2π×环宽 6.28
【详解】(1)3.14×(10+1×2)﹣3.14×10
=3.14×12﹣31.4
=37.68﹣31.4
=6.28(米);
答:如果圆环的小圆直径是10米,那么大圆周长比小圆周长长6.28米.
(2)如果小圆直径是d米,大圆的直径是(d+2)米,那么大圆周长比小圆周长长π(d+2﹣d)=2π米.
答:当小圆直径是d米时,大圆周长比小圆周长长2π米.
(3)完成以上2题后,发现大圆周长比小圆周长长2π×环宽,如果圆环的宽度还是1米,小圆直径是2015米,大圆周长比小圆周长长6.28米.
故答案为6.28.
8.25平方厘米
【分析】根据图形的特点,把半圆内的阴影部分从右边割下补到左边,阴影部分即成为一个上底是6厘米,下底是(14-5×2)厘米,高是5厘米的梯形,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【详解】如图:
[6+(14-5×2)]×5÷2
=[6+4]×5÷2
=10×5÷2
=25(平方厘米)
答:阴影部分的面积是25平方厘米。
【点睛】本题考查求阴影部分的面积,解答本题的关键是通过割补法使阴影部分拼成一个梯形,然后根据梯形的面积公式解答。
9.(1)(3)(4)见详解
(2)12.56a2;
(5)东南
【分析】(1)点与直线的距离,垂线段最短。
(2)在正方形内画一个最大的圆,则该圆的直径相当于正方形的边长,然后根据圆的面积公式:S=πr2,据此解答即可。
(3)点P不动,其他各点顺时针旋转90°之后,顺次连接即可。
(4)根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,找到各点然后连接,最后再向下平移3格即可。
(5)根据“上北下南,左西右东”及图中的信息判断即可。
【详解】(1)(3)(4)如图所示:
(2)3.14×(2a)2=12.56a2(平方厘米)
(5)以A点为观测点,那么C点在A点的(东南)方向。
【点睛】本题考查平移和旋转,明确旋转角度、旋转中心和旋转方向是解题的关键。
10.266.9平方厘米
【分析】设大圆的半径为,小圆的半径为,环形的面积,又因阴影部分的面积平方厘米(大三角形面积减去小三角形面积),从而就可以求出环形的面积。
【详解】解:设大圆的半径为,小圆的半径为,
因为,
则环形的面积:
(平方厘米)
答:环形的面积是266.9平方厘米。
【点睛】解答此题的关键是得出的值,利用等量代换即可求出环形的面积。
11.43.96平方米
【分析】根据圆环的面积公式求出整个环形的面积,阴影部分的面积是整个环形面积的一半,据此解答。
【详解】3.14×[(6+2)2-62]÷2
=3.14×[64-36]÷2
=3.14×28÷2
=87.92÷2
=43.96(平方米)
答:小路的面积是43.96平方米。
【点睛】掌握环形的面积计算公式是解答题目的关键。
12.5周
【分析】根据圆的周长公式,,求出油桶滚动一圈的距离,由于油桶在两侧墙内滚动,所以油桶要滚过的路程是(16.2-0.5)m,再除以油桶滚动一圈的距离就是要求的答案。
【详解】(16.2-0.5)÷(2×3.14×0.5)
=15.7÷3.14
=5(周)
答:需要转动5周。
【点睛】此题主要考查圆的周长在实际生活中的应用,关键是熟记圆的周长公式。
13.113.04平方厘米
【分析】通过正方形的周长公式:C=4a,代入周长求出正方形的边长,即是这个最大圆的直径,再利用圆的面积公式:S=,先算出半径后,然后代入即可得解。
【详解】48÷4=12(厘米)
3.14×(12÷2)2
=3.14×6×6
=113.04(平方厘米)
答:这个圆的面积是113.04平方厘米。
【点睛】此题的解题关键是灵活运用正方形的周长公式和圆的面积公式解决问题。
14.16cm2
【分析】观察图形可知,三角形的底相当于圆的直径,高相当于圆的半径,然后根据三角形的面积=底×高÷2,据此代入数值进行计算即可。
【详解】4×(4×2)÷2
=4×8÷2
=32÷2
=16(cm2)
答:阴影部分三角形的面积是16cm2。
【点睛】本题考查三角形的面积,明确该三角形与圆的关系是解题的关键。
15.0.86平方厘米
【分析】题干图中的左下角的封闭图形就是游戏币无法到达的区域,求出这个区域的面积,再乘4(正方形有四个角,游戏币都无法到达)即可。左下角的封闭图形的面积等于边长是1cm的正方形面积减去四分之一的半径1cm的圆的面积。
【详解】
(cm2)
答:在正方形区域内游戏币不能到达的部分的面积是0.86cm2。
【点睛】本题属于求组合图形面积的问题,根据正方形和圆面积公式解答即可。重在考查学生的分析能力和思维想象能力。
16.56.52平方米
【分析】根据题意,时针12小时转一圈,一天是24小时,时针相当于转了2圈,求时针走过的面积就是求半径为3米的圆的面积,根据圆的面积公式:面积=π×半径2,代入数据,求出时针转一圈的面积,再乘2,即可求出时针一天走过的面积。
【详解】3.14×32×2
=3.14×9×2
=28.26×2
=56.52(平方米)
答:它一天走过的面积大约是56.52平方米。
【点睛】解答本题的关键明确时针走了一天,是转了2圈;以及利用圆的面积公式进行解答。
17.(1)0.86平方厘米
(2)图形见详解;3.44平方厘米
【分析】(1)由题意可知,小方格的边长的为1厘米,维维完成的图案面积=边长是2厘米正方形的面积-×半径是2厘米圆的面积,根据正方形的面积=边长×边长,圆的面积公式:S=πr2,据此解答即可。
(2)由题意可知,整幅是由这样的4个图形组成,即边长为4厘米的正方形挖掉其正方形中最大的圆,剩下的部分就是完整图案,据此作图即可;然后根据整幅作品的面积=边长是4厘米的正方形的面积-半径是2厘米圆的面积,根据正方形的面积=边长×边长,圆的面积公式:S=πr2,据此解答即可。
【详解】(1)2×2-×3.14×22
=4-3.14
=0.86(平方厘米)
答:维维完成的图案面积是0.86平方厘米。
(2)如图:
4×4-3.14×22
=16-12.56
=3.44(平方厘米)
答:整幅作品的面积是3.44平方厘米。
【点睛】本题考查正方形和圆的面积,熟记公式是解题的关键。
18.39.25平方米
【分析】由题意知道,15.7米就是鸡场的周长,也是圆周长的一半,根据圆的周长公式:,求出半圆的半径,再根据圆的面积:,求出其面积。
【详解】15.7×2÷3.14÷2
=31.4÷3.14÷2
=10÷2
=5(米)
3.14×52÷2
=3.14×25÷2
=78.5÷2
=39.25(平方米)
答:这个养鸡场的面积是39.25平方米。
【点睛】本题考查圆的周长、面积公式的应用,熟练掌握公式即可解答。
19.问号
【分析】大圆的半径R与小圆的半径r之间的长度为2∶1,可得大圆的半径R=2r,利用圆环的面积公式:S=以及圆的面积公式:S=和S=,分别计算句号、逗号、问号的面积,比较面积的大小,即可得出哪个标点符号的油漆用得最多。
【详解】句号的面积:
=
=
逗号的面积:
=
=
=
问号的面积:
=
=
=
=
<<
答:画问号的油漆用得最多。
【点睛】此题的解题关键是灵活运用圆的面积以及圆环的面积公式解决实际的问题。
20.(1)49.5米;(2)能;理由见详解。
【分析】(1)长与宽的比是4∶3,可把长看作4份,宽看作3份,长方形的长约66米,66除以6求出1份所占的长度,再乘宽所占的份数,即可求出这个场地的宽度。
(2)同学们两臂展开的平均距离是1.5米,乘100得到圆的周长,用圆的周长公式可求出圆的直径,与这个场地的宽比较,即可得出结论。
【详解】(1)长与宽的比是4∶3,
66÷4×3
=16.5×3
=49.5(米)
答:这个场地的宽大约是49.5米。
(2)100×1.5=150(米)
150÷3.14≈47.77(米)
47.77<49.5
答:这个场地能容纳下这个圆,因为这个场地的宽都比圆的直径大。
【点睛】此题主要根据比的应用,转化成份数求解,然后利用圆的周长公式,解决实际问题。
21.628平方厘米
【分析】根据图示所知,圆心角是45°,45°÷360°=,即CD边扫过的面积是以CD边为半径的圆的面积的,利用圆的面积公式S=代入即可得解。
【详解】45°÷360°=45÷360=0.125=
3.14×402×
=3.14×1600×
=628(平方厘米)
答:CD边扫过的面积的是628平方厘米。
【点睛】本题主要考查阴影图形的面积,关键是利用圆的面积公式求解。
22.周长相等;大圆中阴影部分的面积比两个小圆的面积和小。
【分析】由图知道两个小圆的直径和正好等于大圆的直径,假设最小的圆的直径是2,较小的圆的直径是4,利用圆的周长和面积公式分别求三个圆的周长和面积进行比较即可求出结果。
【详解】解:设最小的圆的直径是2,较小的圆的直径是4,
两个小圆周长和:2×3.14+4×3.14
=6.28+12.56
=18.84
大圆周长和:3.14×(2+4)
=3.14×6
=18.84
18.84=18.84
所以大圆的周长与两个小圆周长的和相等。
两个圆面积和:
3.14×(2÷2)2+3.14×(4÷2)2
=3.14×1+3.14×4
=3.14+12.56
=15.7
大圆面积:
3.14×[(2+4)÷2]2
=3.14×[6÷2]2
=28.26
阴影部分:
28.26-15.7=12.56
12.56<15.7
所以大圆中阴影部分的面积比两个小圆的面积和小。
答:大圆的周长与两个小圆周长的和相等,大圆中阴影部分的面积比两个小圆的面积和小。
【点睛】本题主要是灵活利用圆的周长和面积公式解决问题。
23.2390.12平方厘米
【分析】已知灶台面板长75厘米、宽42厘米,利用长方形的面积公式:S=ab,可计算出灶台面板的面积,已知锅撑圈直径是22厘米,利用圆的面积公式:S=,可计算出两个锅撑圈的面积,用灶台面板的面积减去两个锅撑圈的面积,即可求出需要清污的面积。
【详解】
=
=
=
=(平方厘米)
答:清污(锅撑圈部分除外)的面积是2390.12平方厘米。
【点睛】此题的解题关键是灵活运用长方形和圆的面积公式解决实际的问题。
24.7.74平方分米
【分析】由题意可知,两个小圆的直径和相当于正方形的一条边长,进而求出小圆的面积,然后用正方形的面积减去4个圆的面积即可。
【详解】6÷2÷2
=3÷2
=1.5(分米)
6×6-3.14×1.52×4
=36-28.26
=7.74(平方分米)
答:剩下的铁皮面积是7.74平方分米。
【点睛】本题考查圆的面积,明确两个小圆的直径和相当于正方形的边长是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末应用题特训:圆(易错篇)数学六年级上册人教版
1.在一个直径是25m的圆形场地周围栽树.每隔1.57m 栽一棵,一共可以栽多少棵
2.丽丽想用一根长18cm的彩带装饰一个半径为3cm的圆形化妆镜,请你估一估,彩带够吗?为什么?
3.一辆自行车的外轮直径是60cm,如果平均每分钟转100圈,通过一座长3768m的大桥,需要多少分钟?
4.用一根长8米的绳子围着一棵树绕4圈,还余1.72米。这棵树的直径约是多少米?
5.请先画出一个长是3厘米,宽是2厘米的长方形,再在这个长方形中画一个最大的圆,然后求出这个圆形的面积.
6.一个圆的半径是6厘米,在这个圆内画一个最大的正方形。这个正方形的面积是多少平方厘米?
7.如图是一个环形,已知圆环宽度是1米.
(1)如果圆环的小圆直径是10米,那么大圆周长比小圆周长长多少米?
(2)当小圆直径是d米时,大圆周长比小圆周长长多少米?
建议:小圆直径是d米,大圆的直径是d+…,建议列出综合算式解答.
(3)完成以上2题后,你有什么发现?如果圆环的宽度还是1米,小圆直径是2015米,大圆周长比小圆周长长 米.
提示:不需写过程,直接填答案
8.如图四边形ABCD为梯形,半圆的半径OD长为5cm,求阴影部分的面积。
9.
(1)画出点E到直线a的距离。
(2)在正方形内画一个最大的圆,如果每个小方格的边长是a厘米,那么所画圆的面积是( )平方厘米。
(3)画出梯形绕点P顺时针方向旋转90°之后的图形。
(4)描出A(12,9),B(16,9),C(13,7)三点并顺次连接,得到图形ABC,然后画出图形ABC向下平移3格后的图形。
(5)以A点为观测点,那么C点在A点的( )方向。
10.如图所示,阴影部分的面积是85平方厘米,圆环的面积是多少平方厘米?(π取3.14)
11.如图所示:沿半圆形草坪铺一条2米宽的小路,小路的面积是多少平方米?
12.地面上横躺着一个底面半径为0.5m的圆柱形油桶,如果要将这个油桶推到与它相距16.2m的墙边(如图),需要转动几周?
13.已知一个正方形的周长是48厘米,在这个正方形中画一个最大的圆,这个圆的面积是多少平方厘米?
14.下图中圆的半径是4cm,求阴影部分三角形的面积。
15.如图,一枚半径为1cm的游戏币在边长为6cm的正方形区域内任意移动。在正方形区域内游戏币不能到达的部分的面积是多少cm2?
16.王老师读小学时,华蓥市的标志性建筑之一——钟鼓楼(如图)十分高大,楼上的钟面上的时针大约长3米,那么它一天走过的面积大约有多少平方米?
17.维维在方格纸中绘制图案,他只完成了整幅作品的。(如下图)
(1)维维完成的图案面积是多少平方厘米?
(2)将整幅作品补充完整,并计算整幅作品的面积。
18.刘大爷用篱笆靠墙围一个半圆形(直径靠墙)的养鸡场,篱笆的长度为15.7米。这个养鸡场的面积是多少平方米?
19.某开发区大标语牌上要画出如下图所示的三种标点符号:句号、逗号、问号。已知大圆半径相同,都为R;小圆半径也相同,都为r;而且。如果都是均匀用料,画哪个标点符号的油漆用得最多?
20.实验小学六年级在一个长方形的场地开展集体舞活动演练,并在场地中进行队列变换。
(1)如果长方形长约66米,长方形场地长与宽的比是4∶3。那么这个场地的宽大约是多少米?
(2)如果从中选出100名同学,在场地中两臂展开围成一个尽可能大的请判断这个场地能否容纳下这个圆,并说明理由。(同学们两臂展开的平均距离是1.5米)
21.计算长方形ABDC绕点D顺时针旋转45°时,CD边扫过的面积。
22.计算并回答下面的问题。
如图所示,大圆中有两个小圆,且两个小圆的直径和正好等于大圆的直径。请问:大圆的周长与两个小圆周长的和相比,谁大些?大圆中阴影部分的面积与两个小圆面积的和相比,谁大些?
23.小军家的煤气灶台面板被油渍弄污了,妈妈要清洁面板。已知这个灶台面板长75厘米、宽42厘米,锅撑圈直径是22厘米,清污(锅撑圈部分除外)的面积是多少平方厘米?
24.在一块边长6分米的正方形铁皮上剪去4个大小相等的圆(如图),剩下的铁皮面积是多少平方分米?
参考答案:
1.50棵
【详解】3.14×25÷1.57=50(棵)
2.不够;估小了还不够,精确计算更不够
【分析】根据圆的周长=2πr,求出化妆镜周长,与彩带长度比较即可。
【详解】2×3.14×3≈18(厘米)
18=18
答:彩带不够,因为将π看成3估出来还不够,看成3.14肯定不够。
【点睛】关键是掌握圆的周长公式。
3.20分钟
【分析】根据圆的周长公式C=πd,先求出自行车外轮转一圈走的路程,再乘100圈,即是自行车外轮平均每分钟走的路程;求通过一座大桥需要的时间,根据时间=路程÷速度,用大桥的长度除以自行车每分钟走的路程即可;注意单位的换算:1m=100cm。
【详解】3.14×60×100
=188.4×100
=18840(cm)
3768m=376800cm
376800÷18840=20(分钟)
答:需要20分钟。
【点睛】掌握圆的周长公式,明确速度、时间、路程三者之间的关系解题的关键。
4.0.5米
【分析】在绳子的总长中减去剩余的1.72米,既是这个树干的4个周长,就可求出这棵树的直径。
【详解】
=6.28÷4÷3.14
=1.57÷3.14
=0.5(米)
答:这棵树的直径约是0.5米。
5.如图,面积是3.14平方厘米
【详解】试题分析:根据所给条件,先画一个长3厘米,宽2厘米的长方形,再以长方形的对角线的交点为圆心,以2÷2=1厘米为半径,即可画出符合要求的圆,然后再求出这个圆的面积.
解:先画一个长3厘米,宽2厘米的长方形,再长方形内画一个直径是2厘米的圆;
这个圆的面积是:3.14×(2÷2)2=3.14×1=3.14(平方厘米);
如图:
.
点评:本题是考查指定长、宽画长方形,指定半径画圆及圆面积的计算.画圆时,圆心决定圆的位置,半径(直径)决定圆的大小.
6.72平方厘米
【分析】根据题意,在圆内画一个最大的正方形,用正方形的一条对角线把这个正方形分成两个完全一样的三角形,三角形的底等于圆的直径,三角形的高等于圆的半径,根据三角形的面积=底×高÷2,即可求出一个三角形的面积,再乘2,就是这个正方形的面积。
【详解】圆的直径:6×2=12(厘米)
三角形的面积:
12×6÷2
=72÷2
=36(平方厘米)
正方形的面积:
36×2=72(平方厘米)
答:这个正方形的面积是72平方厘米。
【点睛】掌握圆内最大正方形的面积求法,把正方形的面积转移到两个三角形的面积上,找出三角形的底、高与圆的半径的关系,然后运用三角形的面积公式求解。
7.(1)6.28米 (2)2π米 (3)发现大圆周长比小圆周长长2π×环宽 6.28
【详解】(1)3.14×(10+1×2)﹣3.14×10
=3.14×12﹣31.4
=37.68﹣31.4
=6.28(米);
答:如果圆环的小圆直径是10米,那么大圆周长比小圆周长长6.28米.
(2)如果小圆直径是d米,大圆的直径是(d+2)米,那么大圆周长比小圆周长长π(d+2﹣d)=2π米.
答:当小圆直径是d米时,大圆周长比小圆周长长2π米.
(3)完成以上2题后,发现大圆周长比小圆周长长2π×环宽,如果圆环的宽度还是1米,小圆直径是2015米,大圆周长比小圆周长长6.28米.
故答案为6.28.
8.25平方厘米
【分析】根据图形的特点,把半圆内的阴影部分从右边割下补到左边,阴影部分即成为一个上底是6厘米,下底是(14-5×2)厘米,高是5厘米的梯形,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【详解】如图:
[6+(14-5×2)]×5÷2
=[6+4]×5÷2
=10×5÷2
=25(平方厘米)
答:阴影部分的面积是25平方厘米。
【点睛】本题考查求阴影部分的面积,解答本题的关键是通过割补法使阴影部分拼成一个梯形,然后根据梯形的面积公式解答。
9.(1)(3)(4)见详解
(2)12.56a2;
(5)东南
【分析】(1)点与直线的距离,垂线段最短。
(2)在正方形内画一个最大的圆,则该圆的直径相当于正方形的边长,然后根据圆的面积公式:S=πr2,据此解答即可。
(3)点P不动,其他各点顺时针旋转90°之后,顺次连接即可。
(4)根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,找到各点然后连接,最后再向下平移3格即可。
(5)根据“上北下南,左西右东”及图中的信息判断即可。
【详解】(1)(3)(4)如图所示:
(2)3.14×(2a)2=12.56a2(平方厘米)
(5)以A点为观测点,那么C点在A点的(东南)方向。
【点睛】本题考查平移和旋转,明确旋转角度、旋转中心和旋转方向是解题的关键。
10.266.9平方厘米
【分析】设大圆的半径为,小圆的半径为,环形的面积,又因阴影部分的面积平方厘米(大三角形面积减去小三角形面积),从而就可以求出环形的面积。
【详解】解:设大圆的半径为,小圆的半径为,
因为,
则环形的面积:
(平方厘米)
答:环形的面积是266.9平方厘米。
【点睛】解答此题的关键是得出的值,利用等量代换即可求出环形的面积。
11.43.96平方米
【分析】根据圆环的面积公式求出整个环形的面积,阴影部分的面积是整个环形面积的一半,据此解答。
【详解】3.14×[(6+2)2-62]÷2
=3.14×[64-36]÷2
=3.14×28÷2
=87.92÷2
=43.96(平方米)
答:小路的面积是43.96平方米。
【点睛】掌握环形的面积计算公式是解答题目的关键。
12.5周
【分析】根据圆的周长公式,,求出油桶滚动一圈的距离,由于油桶在两侧墙内滚动,所以油桶要滚过的路程是(16.2-0.5)m,再除以油桶滚动一圈的距离就是要求的答案。
【详解】(16.2-0.5)÷(2×3.14×0.5)
=15.7÷3.14
=5(周)
答:需要转动5周。
【点睛】此题主要考查圆的周长在实际生活中的应用,关键是熟记圆的周长公式。
13.113.04平方厘米
【分析】通过正方形的周长公式:C=4a,代入周长求出正方形的边长,即是这个最大圆的直径,再利用圆的面积公式:S=,先算出半径后,然后代入即可得解。
【详解】48÷4=12(厘米)
3.14×(12÷2)2
=3.14×6×6
=113.04(平方厘米)
答:这个圆的面积是113.04平方厘米。
【点睛】此题的解题关键是灵活运用正方形的周长公式和圆的面积公式解决问题。
14.16cm2
【分析】观察图形可知,三角形的底相当于圆的直径,高相当于圆的半径,然后根据三角形的面积=底×高÷2,据此代入数值进行计算即可。
【详解】4×(4×2)÷2
=4×8÷2
=32÷2
=16(cm2)
答:阴影部分三角形的面积是16cm2。
【点睛】本题考查三角形的面积,明确该三角形与圆的关系是解题的关键。
15.0.86平方厘米
【分析】题干图中的左下角的封闭图形就是游戏币无法到达的区域,求出这个区域的面积,再乘4(正方形有四个角,游戏币都无法到达)即可。左下角的封闭图形的面积等于边长是1cm的正方形面积减去四分之一的半径1cm的圆的面积。
【详解】
(cm2)
答:在正方形区域内游戏币不能到达的部分的面积是0.86cm2。
【点睛】本题属于求组合图形面积的问题,根据正方形和圆面积公式解答即可。重在考查学生的分析能力和思维想象能力。
16.56.52平方米
【分析】根据题意,时针12小时转一圈,一天是24小时,时针相当于转了2圈,求时针走过的面积就是求半径为3米的圆的面积,根据圆的面积公式:面积=π×半径2,代入数据,求出时针转一圈的面积,再乘2,即可求出时针一天走过的面积。
【详解】3.14×32×2
=3.14×9×2
=28.26×2
=56.52(平方米)
答:它一天走过的面积大约是56.52平方米。
【点睛】解答本题的关键明确时针走了一天,是转了2圈;以及利用圆的面积公式进行解答。
17.(1)0.86平方厘米
(2)图形见详解;3.44平方厘米
【分析】(1)由题意可知,小方格的边长的为1厘米,维维完成的图案面积=边长是2厘米正方形的面积-×半径是2厘米圆的面积,根据正方形的面积=边长×边长,圆的面积公式:S=πr2,据此解答即可。
(2)由题意可知,整幅是由这样的4个图形组成,即边长为4厘米的正方形挖掉其正方形中最大的圆,剩下的部分就是完整图案,据此作图即可;然后根据整幅作品的面积=边长是4厘米的正方形的面积-半径是2厘米圆的面积,根据正方形的面积=边长×边长,圆的面积公式:S=πr2,据此解答即可。
【详解】(1)2×2-×3.14×22
=4-3.14
=0.86(平方厘米)
答:维维完成的图案面积是0.86平方厘米。
(2)如图:
4×4-3.14×22
=16-12.56
=3.44(平方厘米)
答:整幅作品的面积是3.44平方厘米。
【点睛】本题考查正方形和圆的面积,熟记公式是解题的关键。
18.39.25平方米
【分析】由题意知道,15.7米就是鸡场的周长,也是圆周长的一半,根据圆的周长公式:,求出半圆的半径,再根据圆的面积:,求出其面积。
【详解】15.7×2÷3.14÷2
=31.4÷3.14÷2
=10÷2
=5(米)
3.14×52÷2
=3.14×25÷2
=78.5÷2
=39.25(平方米)
答:这个养鸡场的面积是39.25平方米。
【点睛】本题考查圆的周长、面积公式的应用,熟练掌握公式即可解答。
19.问号
【分析】大圆的半径R与小圆的半径r之间的长度为2∶1,可得大圆的半径R=2r,利用圆环的面积公式:S=以及圆的面积公式:S=和S=,分别计算句号、逗号、问号的面积,比较面积的大小,即可得出哪个标点符号的油漆用得最多。
【详解】句号的面积:
=
=
逗号的面积:
=
=
=
问号的面积:
=
=
=
=
<<
答:画问号的油漆用得最多。
【点睛】此题的解题关键是灵活运用圆的面积以及圆环的面积公式解决实际的问题。
20.(1)49.5米;(2)能;理由见详解。
【分析】(1)长与宽的比是4∶3,可把长看作4份,宽看作3份,长方形的长约66米,66除以6求出1份所占的长度,再乘宽所占的份数,即可求出这个场地的宽度。
(2)同学们两臂展开的平均距离是1.5米,乘100得到圆的周长,用圆的周长公式可求出圆的直径,与这个场地的宽比较,即可得出结论。
【详解】(1)长与宽的比是4∶3,
66÷4×3
=16.5×3
=49.5(米)
答:这个场地的宽大约是49.5米。
(2)100×1.5=150(米)
150÷3.14≈47.77(米)
47.77<49.5
答:这个场地能容纳下这个圆,因为这个场地的宽都比圆的直径大。
【点睛】此题主要根据比的应用,转化成份数求解,然后利用圆的周长公式,解决实际问题。
21.628平方厘米
【分析】根据图示所知,圆心角是45°,45°÷360°=,即CD边扫过的面积是以CD边为半径的圆的面积的,利用圆的面积公式S=代入即可得解。
【详解】45°÷360°=45÷360=0.125=
3.14×402×
=3.14×1600×
=628(平方厘米)
答:CD边扫过的面积的是628平方厘米。
【点睛】本题主要考查阴影图形的面积,关键是利用圆的面积公式求解。
22.周长相等;大圆中阴影部分的面积比两个小圆的面积和小。
【分析】由图知道两个小圆的直径和正好等于大圆的直径,假设最小的圆的直径是2,较小的圆的直径是4,利用圆的周长和面积公式分别求三个圆的周长和面积进行比较即可求出结果。
【详解】解:设最小的圆的直径是2,较小的圆的直径是4,
两个小圆周长和:2×3.14+4×3.14
=6.28+12.56
=18.84
大圆周长和:3.14×(2+4)
=3.14×6
=18.84
18.84=18.84
所以大圆的周长与两个小圆周长的和相等。
两个圆面积和:
3.14×(2÷2)2+3.14×(4÷2)2
=3.14×1+3.14×4
=3.14+12.56
=15.7
大圆面积:
3.14×[(2+4)÷2]2
=3.14×[6÷2]2
=28.26
阴影部分:
28.26-15.7=12.56
12.56<15.7
所以大圆中阴影部分的面积比两个小圆的面积和小。
答:大圆的周长与两个小圆周长的和相等,大圆中阴影部分的面积比两个小圆的面积和小。
【点睛】本题主要是灵活利用圆的周长和面积公式解决问题。
23.2390.12平方厘米
【分析】已知灶台面板长75厘米、宽42厘米,利用长方形的面积公式:S=ab,可计算出灶台面板的面积,已知锅撑圈直径是22厘米,利用圆的面积公式:S=,可计算出两个锅撑圈的面积,用灶台面板的面积减去两个锅撑圈的面积,即可求出需要清污的面积。
【详解】
=
=
=
=(平方厘米)
答:清污(锅撑圈部分除外)的面积是2390.12平方厘米。
【点睛】此题的解题关键是灵活运用长方形和圆的面积公式解决实际的问题。
24.7.74平方分米
【分析】由题意可知,两个小圆的直径和相当于正方形的一条边长,进而求出小圆的面积,然后用正方形的面积减去4个圆的面积即可。
【详解】6÷2÷2
=3÷2
=1.5(分米)
6×6-3.14×1.52×4
=36-28.26
=7.74(平方分米)
答:剩下的铁皮面积是7.74平方分米。
【点睛】本题考查圆的面积,明确两个小圆的直径和相当于正方形的边长是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
